变式教学：提升小学高年级儿童数学思维的重要支点

江苏省苏州科技城西渚实验小学校 赵美玲

在科学、经济、社会格局瞬息万变的当今社会，数学的学习，知识的习得仅仅是第一步，学习的最终目标是思维的培养。变式教学是初中数学教学中最常见的一种教学方式，也是培养学生思维的一种有效途径。合理运用变式教学对提升学生思维力和提高教师数学教学效能有着重要的作用。

一、小学数学“变式教学”的基本内涵和独特价值

（一）“变式教学”的基本内涵

所谓变式教学是指在数学教学过程中为了加深学生对于课本中基本概念、性质、定理公式等的理解，教师有目的、有计划地从不同角度做出改变，保留问题的本质特征、改变问题中非本质条件，或将问题升华，从而引发学生灵活思考、提升学生的数学思维高度的教学方法。

（二）“变式教学”对提升数学教学效能的独特价值

变式教学的过程不仅仅是对基础知识的巩固，对基本技能和数学思维的训练，也是学生情感态度形成的重要途经之一，有利于提高学生分析数学问题、解决数学问题的能力。在变式的过程中激发学生思考，长期下来可以使学生思维更具广度和深度，也能培养学生思维的灵活性、创造性，进而激发学生学习的兴趣。

二、当下小学数学教学的现状分析

当下的教学中，小至幼儿园大到高中都在进行素质教育，但是在激烈的升学压力下，教师及家长都在搞“题海战术”。尤其是在小学阶段，大多数小学生的数学思维能力发展还处于低水平阶段，有时有些常见题型没办法深入理解，只能靠死记硬背、机械照搬满足学习需求。

有些教师仅仅是教教材，这种低效的课堂教学，使很大一部分学生思维变得狭窄、僵化，缺乏创造性和变通性。对此，作为小学教师，尤其是高年级数学教师，在平时的教学和辅导中要注重学生思维能力的培养。

三、以“变式教学”提升数学教学效能的策略

在小学阶段学生要具备基本的计算能力，会算法，明算理。在学习计算方法和解决实际问题的同时要注意培养学生抽象、概括、推理的能力。同时要求学生具备初步的空间观念，能解决常见平面图形的周长、面积的计算，了解立体几何中长方体、正方体、圆柱、圆锥基本知识，应用解决问题。下文以高年级教学为例，从计算中的变式教学、解决问题中的变式教学、几何问题中的变式教学三个方面阐述变式教学对提升高年级数学教学效能的策略。

（一）计算中的变式教学。抓住问题本质，使变式教学有的放矢

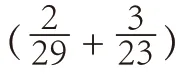
1.计算中一题多解的变式教学

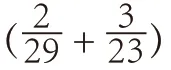
2.计算中一题多变的变式教学

有了以上两种方法的教学，接下来要检验学生对知识本质的掌握情况，避免生搬硬套现象，需要做以下变式教学。

在变式过程中抓住问题本质——乘法分配律和乘法结合律的应用，无论是解法的一题多解还是题目的一题多变，这样的变式教学能满足不同理解能力学生的需求。

（二）解决问题中的变式教学

1.解决问题中多角度变式教学发展学生思维

变式1：一变数据，“甲给乙12.5%后，两数就相等，那么原来甲与乙的比是多少？”

变式2：二变条件或问题，“甲数减少20%后就和乙数一样多，那么原来甲是乙的百分之几？”

变式3：三变深度，“甲数减少20%后就和乙数一样多，那么原来甲比乙多百分之几？”

2.解决问题中的一题多解与多题一解

采用变式思维教学，可以让学生在众多解法中找到适合自己的学习方式和解题思路，透过现象看本质，提炼基本数学规律，类比迁移、触类旁通。

在学习中还会遇到类似问题“修一条路，第一天后已修与未修的比是2：5，第二天修了100 米，此时已修占总路程的30%”。

两个问题看起来好像并不相关，但是其本质相同的。教师通过对这两类典型题的呈现，引导学生分析、比较，归纳出此类问题的特征及解题规律和方法，以后在碰到同类问题时就会快速呈现出解题的步骤。

（三）几何教学中的变式教学

1.几何教学中从正向到逆向

在学生学习三角形面积的计算时，如果已知三角形的底和高，求解三角形的面积，这个问题的解决基本上学生都能掌握，这是正向思维解决问题。但是如果将问题逆向呈现，已知三角形的面积和底，求三角形的高，这时的正确率将会有所下降。经过分析和一段时间的矫正训练错误率会大大降低。逆向问题的解决，需要学生进行稍复杂的推理，这类问题的解决过程中学生的逻辑思维能力会得到提升。

2.变静为动、由浅入深、层层递进

在苏教版六年级下学期平面图形的周长与面积的复习中，有这样一题（见图1）。

图1

有些思维相对不活跃的学生可能很难想到较好的解决方法，如果此时将问题的已知条件减少，问题的难度就进一步加深了，此时就要变静为动（见图2、图3）。

图2

图3

呈现这样的变化过程学生就很容易解决最初的问题。在此基础上也可以进行变式教学。

变式1：求下图灰色部分的面积（见图4）。

这个问题的设计是对上一问题的简单拓展延伸，以便更好地巩固学生对重点问题的理解。

图4

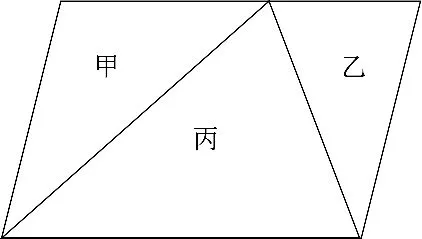
图5

这个问题的设计已经不仅仅是对第一个问题的巩固，这一变式训练将学生的思维提升了一个高度。

变式教学并不是为了解题而解题，变式教学也不能流于形式，每一个变式问题的设计都是为了使学生的思维得到更好的升华。数学是思维的体操，没有思维的数学思考仅仅是模仿与机械的劳动。加强变式教学可以进一步激发学生的求知欲，每一次的变式教学都是学生的一次思维操练，学生可以从多角度去分析问题、养成良好的思维习惯，提高分析问题、解决问题的能力。