试气阶段评价气井不稳定产能的新方法

冯 曦 彭 先 李 骞 赵晓亮 张 平 潘 登

1.中国石油西南油气田公司勘探开发研究院 2.中国石油大学(北京)石油工程学院3.中国石油川庆钻探工程公司工程技术处 4.中国石油川庆钻探工程公司钻采工程技术研究院

0 引言

气井产能评价是天然气勘探开发研究的重要工作之一。其技术内涵主要包括：计算气井绝对无阻流量，预测无阻流量随开井时间增加而变化的规律，分析控制初始无阻流量及其变化特征的主要地质因素，确定气井的合理配产。在测试资料或生产数据充足的条件下，依靠现有气藏工程方法准确评价气井产能并非难事。然而，随着勘探开发一体化模式的普及，气田开发评价及产能建设周期缩短，相关管理和研究工作者经常面临动态资料不充分但又期望在早期能够获得准确认识的情况，在新井试气工作中，这一需求尤为突出。为了避免在短时测试情况下严重误判气井的持续供给能力，对进一步完善气井产能评价方法提出了新的要求。为此，笔者结合近年四川盆地气井试气分析的疑难问题，重点围绕定压生产试井模型的求解与计算，从试井分析理论层面研究了影响气井不稳定产能特征的主控因素，并且面向应用改进了分析预测气井产能变化规律的方法，以期丰富中、高渗透气藏气井产能评价的技术手段，同时促进低渗透、强非均质性等复杂气藏气井产能早期评价问题的解决。

1 现有方法评价不稳定产能的可行性

1.1 以稳定渗流分析为主的方法

1935年Rawlins等[1]提出评价气井产能的稳定试井方法，1959年Katz等[2]奠定修正等时试井分析的基础，这些方法一直沿用至今。针对矿场简化分析的需求，以及特殊类型气藏的复杂地质情况，后续研究又形成了一些补充方法[3-6]。该类方法在应用时至少需要一个稳定生产制度的压力、产量数据，评价结果代表气井当时的“稳定”产能。若储层低渗、强非均质性导致气井产能递减显著，方法适用性将变差。尽管可采用不同时间点稳定渗流分析结果来表征气井产能的变化[7]，但需要较多时间点的测试资料，在早期预测气井产能不稳定特征的能力相对较弱。

1.2 产量递减分析方法

在理论核心层面，生产数据递减分析方法与气井无阻流量递减分析方法有一定相似性，针对前者已有较多研究成果。1945年Arps[8]提出指数递减、双曲递减及调和递减分析模型，1980年Fetkovich[9]在前人研究定压生产试井模型成果的基础上形成了适用范围更广的产量递减分析图版，1991年Blasingame等[10]考虑产量、压力同时递减的普遍现象重新制作了分析图版，1998年Agarwal等[11]针对有限导流和无限导流垂直裂缝井绘制了递减分析图版。该类方法主要用于评价生产井有效控制范围和动用储量，虽然在一定程度上也能预测气井产能的变化，但需要较长时间的生产数据，不太适合早期预测。

1.3 不稳定试井分析方法

不稳定试井分析理论的核心是求解不稳定渗流模型，虽然在此基础上建立的现代产量递减分析方法不适用于气井产能的早期预测，但仍有可供借鉴的研究成果。

基于简单试井模型寻求简化计算公式的研究起源较早，1951年Horner[12]提出的分析方法属于这类成果趋于成熟的典型代表。在解决复杂试井模型研究的关键问题方面，1949年Van Everdingen等[13]采用拉普拉斯变换方法求解不稳定渗流模型，1973年Gringarten等[14]应用格林函数法改进上述模型解的计算，之后Rosa等[15]将Stehfest[16]研究形成的拉普拉斯数值反演算法引入到试井分析。在此基础上，经过数十年发展，形成了现代试井分析的技术框架，以及众多具有不同针对性的分析方法，其中，考虑在定产条件下压力变化的分析方法占主导地位。

在气井不稳定产能评价方面，考虑定压生产的试井模型具有独特的优点。虽然过去已开展了大量研究，形成了较多成果[17-18]，但在面向应用的早期预判、简化计算和可靠性保障方面，仍存在疑难问题，这是长期以来定压试井模型远不如定产模型应用广泛的主要原因。

笔者此次重点关注直井试气分析，探索研究了满足分析预测气井不稳定产能应用需求的改进方法。

2 技术关键点聚焦

2.1 不稳定试井二项式产能方程应用及潜在问题

考虑均质储层直井平面径向不稳定渗流，气井拟压力变化满足以下关系式[19]：

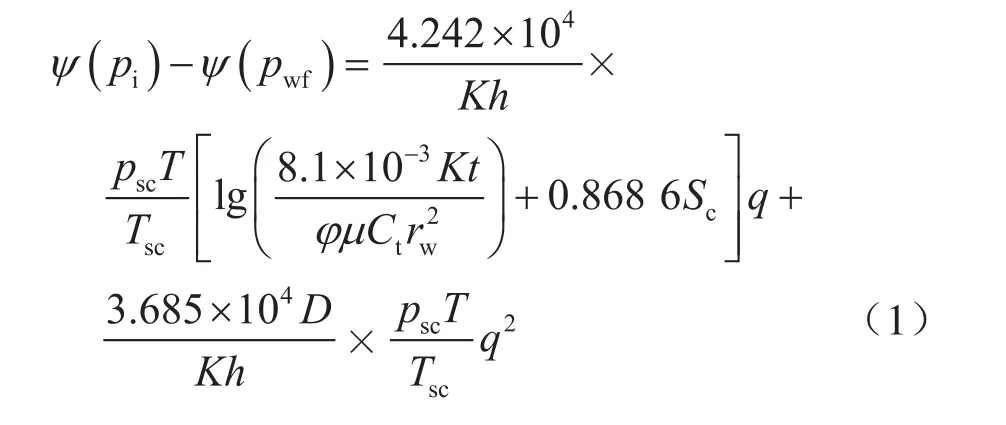
式中Ψ表示拟压力，MPa2/(mPags)；pi、pwf、psc分别表示开井前的地层压力、开井时井底流动压力、标准大气压，MPa；K表示储层渗透率，mD；h表示储层有效厚度，m；T、Tsc分别表示地层温度、标准温度，K；t表示开井时间，h；φ表示孔隙度；μ表示地层条件下天然气黏度，mPags；Ct表示地层流体与岩石的综合压缩系数，MPa－1；rw表示井眼半径，m；Sc表示表征井底污染或改善的净表皮系数，无量纲；q表示气产量，104m3/d；D表示紊流效应影响的非达西流动系数，(104m3/d)－1。公式系数对应于渗透率单位10－3μm2，在采用mD单位时近似相同。

式（1）为一次项系数随时间变化的二项式产能方程，可用于计算不同时刻的无阻流量，前提是测试时间处于常规试井分析的径向流直线特征阶段，不满足这一条件时使用式（1）计算无阻流量容易产生严重偏差，而二项式方程求根的计算方式往往使这种偏差难以被察觉。

2.2 影响常规分析方法适应性的敏感因素

借助定压生产试井模型解的公式，能了解计算气井无阻流量产生偏差的原因。前人已研究确认定压、定产试井模型的长时间渐近解形式相同[20]，有

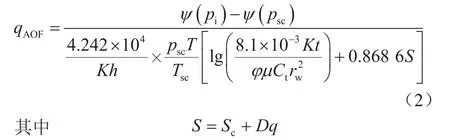
式中qAOF表示气井无阻流量，104m3/d；S表示井底污染或改善以及紊流效应综合影响状况下的总表皮系数（以下简称表皮系数），无量纲。

在储层渗透率低、表皮系数为负且绝对值较大的极端情况下，如果测试时间明显小于径向流直线段起点，则式（2）的计算结果可能为负数；若接近极端状态，即使计算结果为正数，往往也存在较大误差。

2.3 异常情况的根源及其影响程度

式（1）、（2）源自均质地层直井平面径向渗流模型的长时间渐近解。考虑化简前的指数积分表达式，采用有效井径表征表皮效应，无阻流量计算公式为：

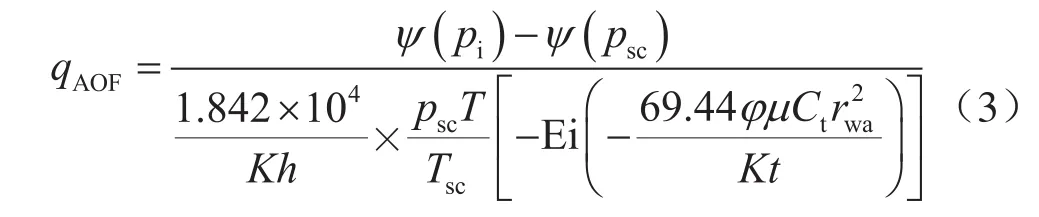
式中rwa表示井底污染或改善以及紊流效应综合影响状况下折算的井眼有效半径，m。

式（3）比式（2）的适用范围广，已没有负数问题，但x增大时，-Ei(-x)急剧变小[21]，如-Ei(-5)约等于0.001 15、-Ei(-10)约等于4.16h10－6，这导致在开井很短时刻计算的无阻流量异常偏高。另一方面，如果忽略紊流表皮效应随产量变化的特点，将较低产量条件下的表皮系数用于式（3），也会使无阻流量计算结果偏大。

以四川盆地产能稳定性较好、有可靠测试分析结果的4口高产气井为例，说明应用式（3）产生的问题。LJ6、D4、LG1、MX10等井通过产能试井（稳定试井或修正等时试井）分析得到的“稳定”无阻流量依次为267.3h104m3/d、758.2h104m3/d、367.9h104m3/d、1 200.6h104m3/d，而采用试井分析商业软件预测无阻流量的变化，初期计算值远远超过1 000h104m3/d（图1），误差很大。

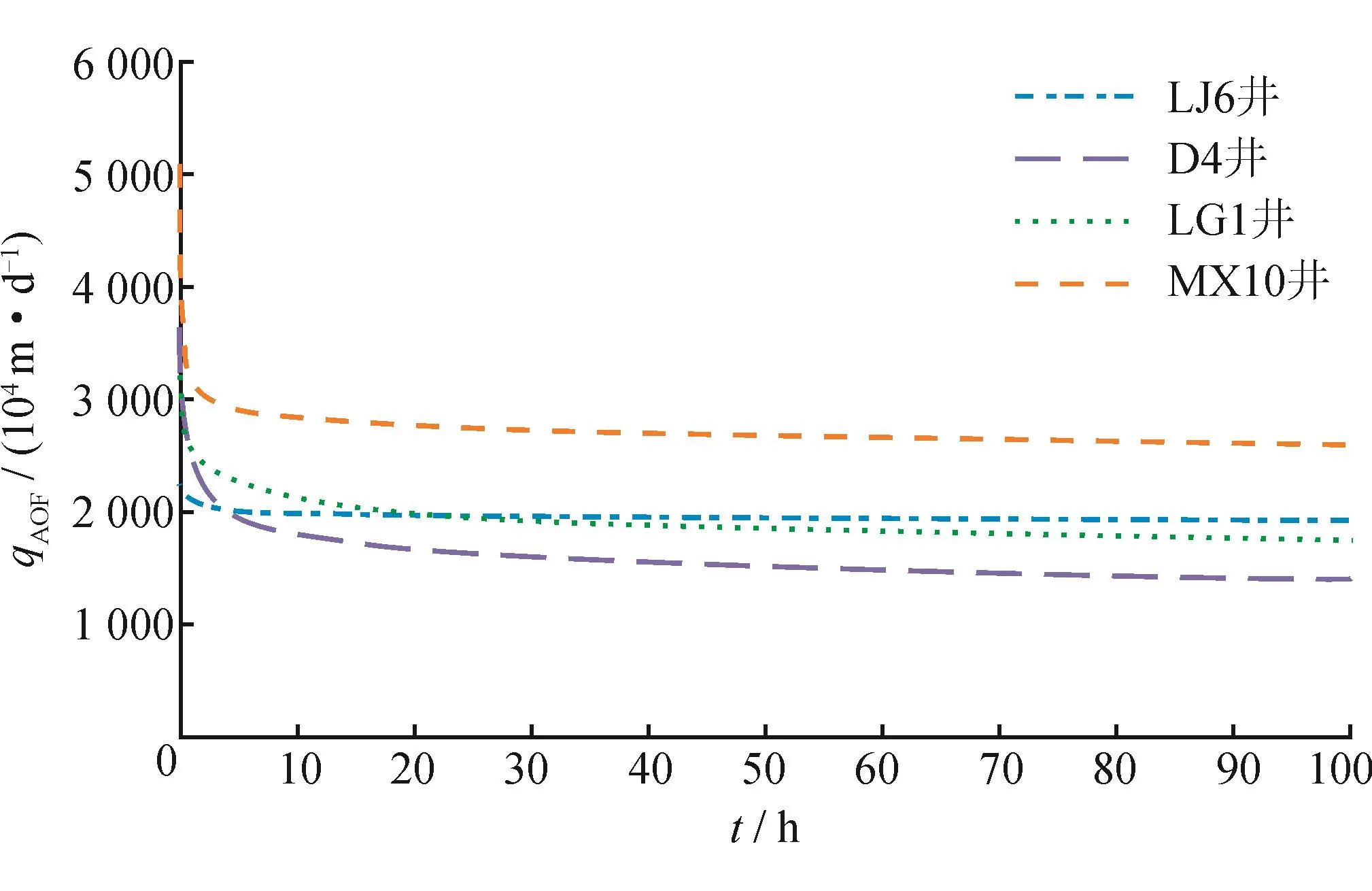
图1 气井初期qAOF变化曲线图（不稳定渗流方法）

定压生产试井模型理论研究早已成形，由于未完全解决上述异常问题，导致长期以来应用较少。

3 气井绝对无阻流量递减公式推导

3.1 定压生产试井模型的无阻流量解析解

采用标准SI单位制进行理论分析，均质储层边界影响出现前气体平面径向渗流方程的通解为[22]：

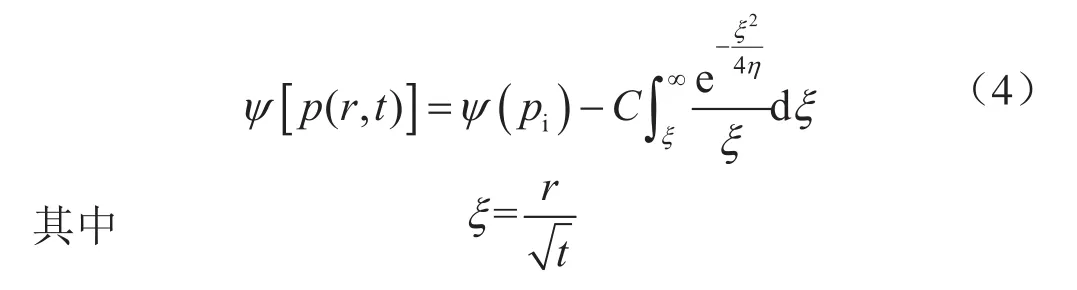
式中r表示到井眼的距离，m；η表示地层导压系数，m2/s；ξ表示公式推导的中间变量，m/s－0.5。

以井底流动压力等于大气压为内边界条件，求解得到井壁以外区域拟压力的计算式为：

无阻流量的计算式则为：

式中Bg表示地层条件下天然气体积系数，无量纲。

3.2 与经典试井理论长时间渐近解的差异

采用国内石油天然气行业标准单位制，考虑有效井径与表皮系数的关系，式（6）转变为：

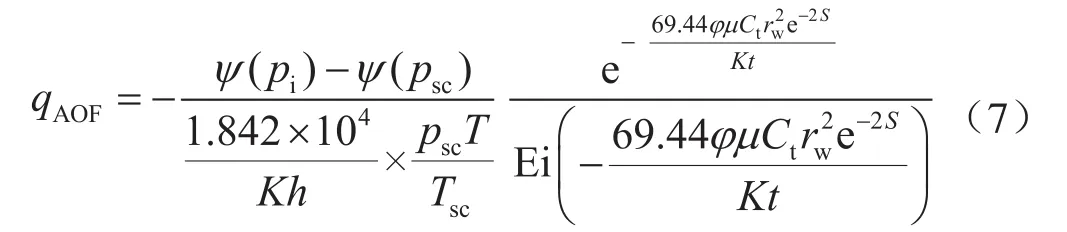
式（7）未做近似性简化处理，适用范围比式（3）更广。若开井时间较长，式（7）中指数项趋于1，过去研究长时间渐近解忽略该项，得到式（3）。在开井初期计算无阻流量时，这种做法容易引起较大计算误差，由此产生如图1所示的异常情况。

笔者根据试井模型精确解，结合指数积分高精度算法[23]，解决了计算公式仅适用于测试时间处于径向流直线时间段的问题，增强了在早期评价气井产能的适应性，并且在长时间条件下计算的准确性完全不受影响，能显著抑制前述异常情况的出现。

4 无阻流量的控制因素分析

4.1 非线性影响关系图版建立及特征分析

由式（7），定义非线性影响因子（σ）为：

根据式（8）计算、绘制得到σ与关系曲线图版（图2），由此，可以通过图版查询来确定σ，再结合式（7），用于计算、比较不同σ值情况下气井产能的差异。

图2 σ与关系曲线图版

为了深入认识主要敏感参数对气井产能的影响规律，拆分后再进行计算分析。设定导压系数与时间的乘积（ηt）变化范围介于（大致涵盖渗透率介于0.01～1 000.00 mD的情况），表皮系数变化范围介于－6～10，根据式（8）计算得到不同参数组合条件下的σ值（表 1）。为简便起见，井眼半径近似取值为0.1 m，该取值不影响对规律的认识。

如表1所示，在ηt小、负表皮系数绝对值大的情况下，计算不收敛，这间接说明了当井底存在大裂缝并且储层渗透率很低时，短时间内难以达到平面径向流供给状态，并定量显示出了平面径向流试井模型完全不适用的范围；同时，当ηt较小（大体对应于渗透率较小、时间较短的情况）时，气井产能对储层改善程度的敏感性较强，而当ηt较大时该敏感性明显降低。

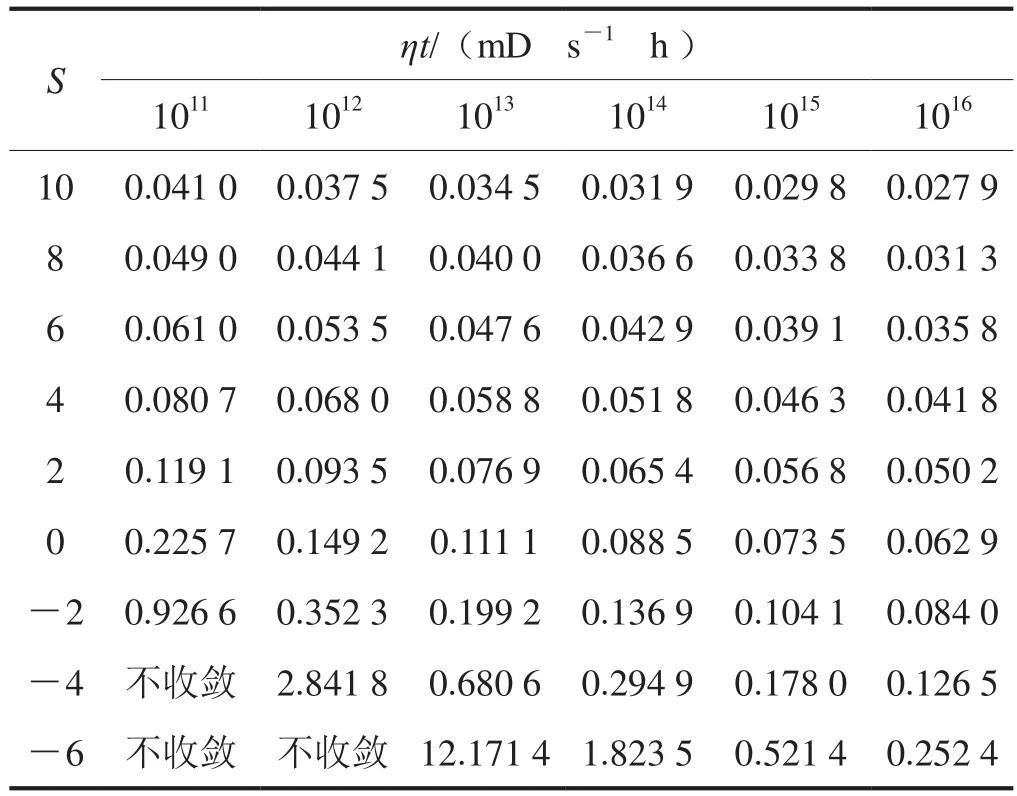
表1 不同S、ηt下σ数据表

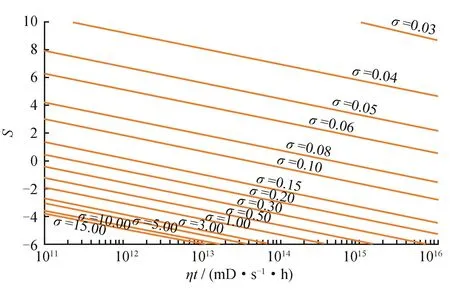
图3 σ与S、ηt关系图版

4.2 无阻流量计算中图版的使用方法

笔者此次重点关注试气评价，这种情况通常有压力恢复测试数据，由此可以分析获得渗透率、表皮系数，在此基础上首先采用图2或图3确定所关注时间点对应的σ值，再用式（7）计算气井无阻流量。在其他的应用情形下，对基础数据的需求和分析方法与之类似。

根据式（7）计算qAOF需要估算在井底压力为大气压的理论假设条件下，由于产量较高导致紊流效应影响严重时的S，这是传统试井分析未涉及的问题，主要解决办法包含以下两种：①当有多个产量制度的试井资料时，分析不同产量对应的S，根据式（2）包含的S—Sc关系式，采用直线回归法确定Sc和D；②当已知某一时刻qAOF时，按式（7）计算与之对应的S，结合试井测试时的产量和由试井解释得到的S，确定Sc和D。若有产能发挥程度较高条件下的生产压差测试数据，可以省去第②种方法中无阻流量、试井解释得到的表皮系数两个条件之一。

在获得Sc和D之后，对任意时间点，先估算qAOF初值，根据S—Sc关系式计算与qAOF对应的S，再按式（7）重新计算qAOF，当相邻两次qAOF计算结果的差值超出允许误差范围时，以最近一次qAOF计算结果为新起点重复上述过程进行迭代计算，直至最终获得相应时刻无阻流量的准确值。

4.3 井底裂缝的影响

在裂缝较长的情况下，平面径向流有效井径等效模型（简称平面径向流等效模型）与无限导流垂直裂缝井模型（简称垂直裂缝井模型）相似性较低，从严格意义上讲文中方法不适用。但是，若气井产能较高，因大产量条件下表皮系数较大，这时即使净表皮系数为负且绝对值较大，新方法也能算出结果，是否近似可用则根据具体情况来定。

以定产量生产试井模型来进行计算分析，结果显示在实际工作常见的裂缝长度、储层渗透率数值区间，两种模型计算结果最大差距不超过15%（图4），对于气井产能评价而言尚可接受。裂缝越长、储层渗透率越低，平面径向流等效模型在长时间情况下的计算误差越大，这时应注意避免误用。

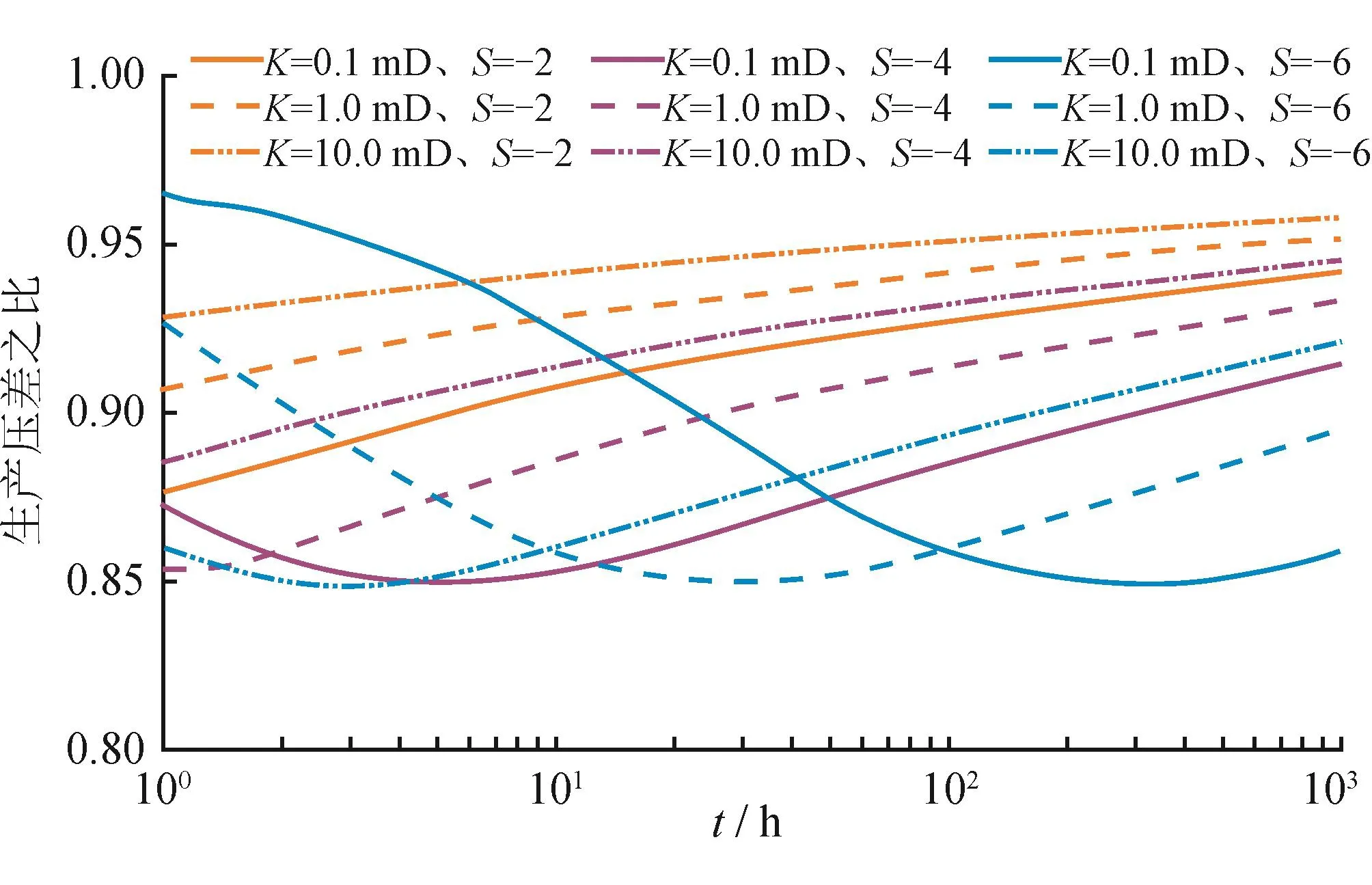
图4 平面径向流等效模型与垂直裂缝井模型计算生产压差之比变化曲线图

4.4 井筒储集效应的影响

气井井筒储集效应显著，前面的试井理论公式推导未考虑该因素，这里增加相关分析。

井筒储集系数对产量的影响式为[24]：

式中qwh表示井口产量，104m3/d；qwb表示井底产量，104m3/d；pw表示井底压力，MPa；pwh表示井口压力，MPa；C表示井筒储集系数，m3/MPa；表示井筒平均压力、平均温度条件下的天然气体积系数，无量纲。

在定井底压力生产的条件下，井筒储集效应影响时间段结束之后，井底与井口压力差值近似不变，此时式（9）导数项为零。这表明只要不涉及开井早期井筒储集效应影响阶段的分析，即使理论模型未考虑该因素，对产能评价的影响也不大。

5 复杂情况下无阻流量的变化特征

5.1 定量分析与定性预判搭配的策略

笔者基于均质无边界地层直井开展研究，形成了快速简便的分析方法，可手工预测气井不稳定产能。针对大型压裂井、水平井、双重介质及复合储层、封闭边界等复杂情况，前述新方法不适用。相关研究涉及拉普拉斯变换求解、无穷级数或积分等计算[25-26]，虽然这方面早已有较多成果[27-29]，并且近年有一些新的探索研究取得成功[30-31]，但基本上都高度依赖计算机、不太适合直观理解与简便分析。

早期预测气井产能，并分析其不稳定特征属长期性疑难问题，诸多研究有待深入。在储层非均质性不强、直井试气的简单情况下可以直接采用前述新方法，在复杂情况下不具备精细定量分析条件时，用新方法也可以提供定性的类比参考，这是现阶段满足实际工作需求的较好方式。

5.2 针对应用关注点的理论分析

以均质储层平面径向流模型为参照，针对大型压裂井、裂缝—孔隙型储层、远井区物性变差的典型情况另做计算研究。将式（7）等号右边与σ无关的部分移至左边，然后定义无量纲无阻流量，再将计算结果进行对比，从而深化对不同类型气井不稳定产能特征存在差异的认识。这里侧重于研究早期阶段气井的产能特征，没有考虑供给边界的影响，图5中设定的较长时间跨度主要用于适配不同渗透率条件下无量纲时间分布区间的不同，而不是为了研究超长时间阶段气井产能的变化规律。

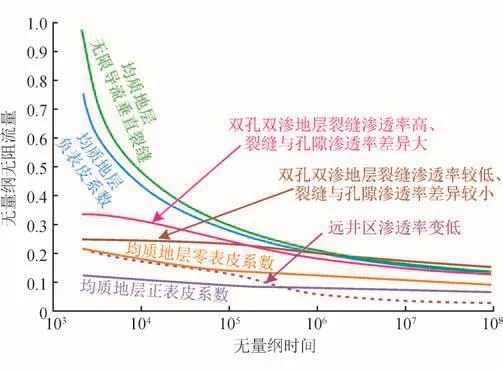
图5 典型井初期无阻流量递减曲线图

5.3 主要规律性认识

如图5所示，当无量纲时间值较小时，负表皮或穿过井底的大裂缝将使气井初期产能大幅度升高，但早期递减快；对于裂缝—孔隙型储层，当裂缝渗透率高但与孔隙搭配关系不好、基质孔隙系统供给严重滞后时，初期产能主要受裂缝渗透率影响，在裂缝主导供给的早期阶段结束后，将出现产能递减较快的阶段；若气藏宏观非均质性较强、远井区储层物性比近井区差，当生产井压力扰动完全传播到远井区之后，将在一定时间阶段表现出产能递减加快的现象。

以上3种情况属于气井初期产能与长期稳产能力差异较大的典型情况。以理论研究获得的认识为指导，在实际工作中针对性地强化地质与动态分析研究，研判是否属于上述典型情况，能在短时测试条件下有效减少对气井产能不稳定特征的误判。

6 新方法的应用

6.1 气井不稳定产能评价的简化参照时间点

不同类型气井无阻流量变化特征差异较大，若未采用统一的时间基准，则不同类型气井产能评价结果的可比性较差，不利于后续研究与应用。四川盆地气井试气多在白天开井测试，连续开井测试一般不超过10 h，在大多数情况下试气期间关井压力恢复测试时间接近或超过3 d。结合实际情况，建议以10 h、3 d、30 d为参照时间点，分别评价开井初期、相对稳定状态及较长时间状态下的无阻流量，依次对应于根据开井实测资料直接分析或适度外推预测、经关井压力恢复实测数据验证的试井模型预测、超出实测数据检验范围具有一定不确定性的长时间预测结果。这样做既减少分析工作量，又便于统一对比不同类型气井产能特征的差异、强化整体认识。

6.2 新方法分析结果的含义及其与类似方法的差异

新方法预测绝对无阻（井底压力为大气压的理论假设）条件下产量变化规律，偏重于揭示不受人为因素影响的本质特征，唯一性较强。过去经常采用变通性处理方法，即根据气井实际生产条件下的压力变化趋势预测后续井底流动压力，再采用产能方程或“一点法”计算相应时刻的无阻流量，侧重于评价特定产量条件下无阻流量的变化规律。在储层渗透率低或单井供给范围小的情况下，其分析结果会因配产不同而明显不一致。

与上述变通性处理方法类似，采用定产量生产试井模型预测井底流动压力的变化，可以分析多个产量条件下后续时刻的无阻流量，但是，由于较难估算与虚拟产量对应的表皮系数，该预测方法的应用受限。

6.3 新方法在GS1井应用

GS1井是四川盆地某特大型碳酸盐岩气藏的发现井，该井于2011年7月在震旦系灯二段试气获工业气流，测试气产量为102.15h104m3/d，测试过程中以稳定产量开井2.4 h，之后关井压力恢复48 h。与新方法应用相关的GS1井基础数据、试气测试与分析数据如表2所示。

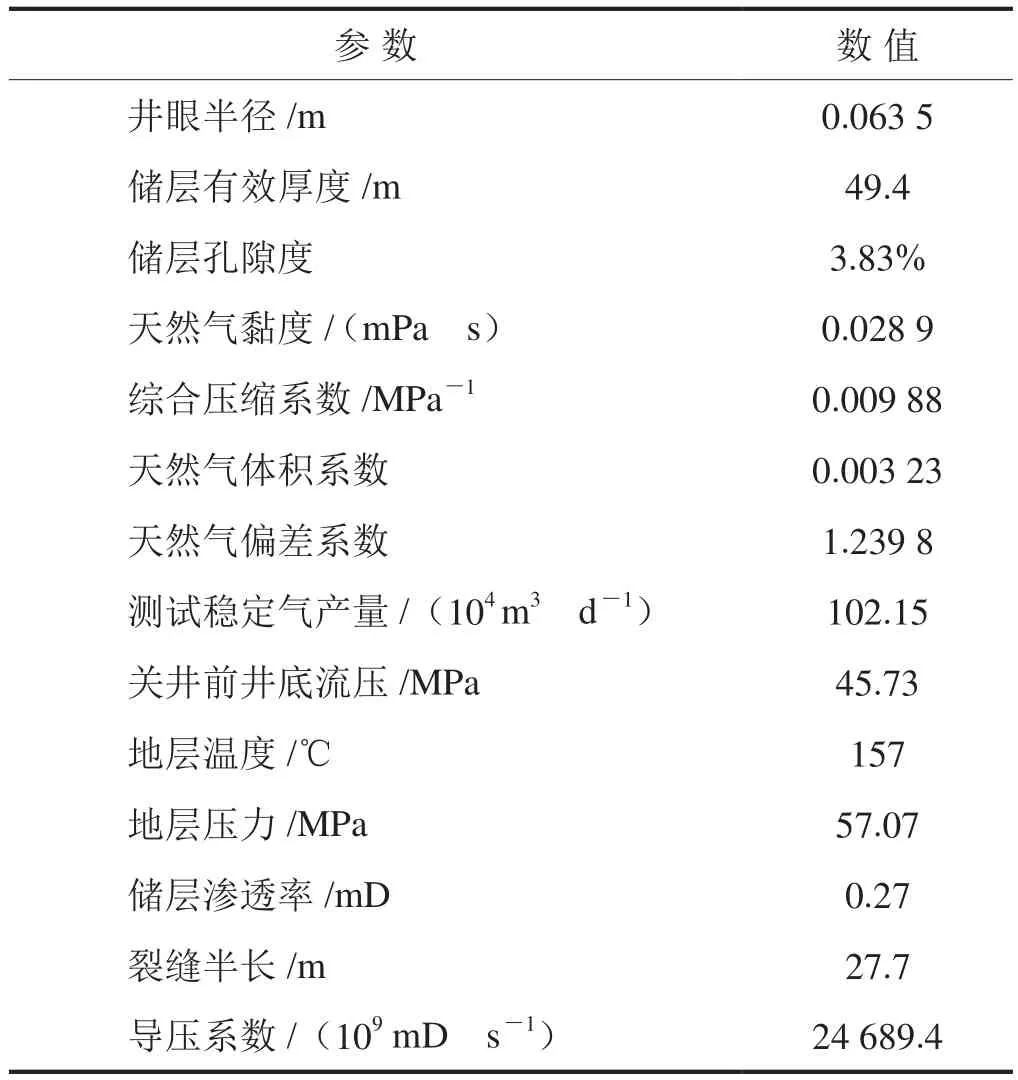
表2 GS1井数据表

GS1井试气解释储层渗透率为0.27 mD；井底存在裂缝发育区，等效于半长为27.7 m的无限导流垂直裂缝；转换为有效井径近似处理模型，计算净表皮系数为－6.078。从图5知这属于初期产能高但递减较快的类型。因此应重点关注该井产能不稳定特征。

GS1井试气时生产压差达到地层压力的20%，属于评价气井产能时采用常规一点法（经验系数α等于0.25）适用性较好的范畴[3,32]，相关研究表明在大生产压差条件下常规一点法计算无阻流量的误差不超过10%，采用该方法计算得到GS1井在开井2.4 h时对应的“稳定”无阻流量为187.77h104m3/d。

根据上述短时开井时刻的qAOF值，用式（7）计算相应条件下的S，其迭代计算方法见下文。该井测试产量达到无阻流量的54.4%，紊流效应的影响反应较充分，根据测试产量及其相应的生产压差，用式（7）迭代计算确定与之对应的S，也能用于后续分析。通过试井分析获得了Sc，计算了初期qAOF，实测q与qAOF的比值较高，满足这三个条件之二，即可计算出非达西流动系数（表3）。

表3 新方法计算GS1井S及D统计表

按前述10 h、3 d、30 d时间点，取表3中第1种方式对应的D值，以一点法计算的“稳定”qAOF为初值，用式（7）估算绝对无阻条件下的S，在此基础上由图2或图3查询得到σ并代入式（7），重新计算相应时刻的qAOF，迭代计算过程如表4所示。

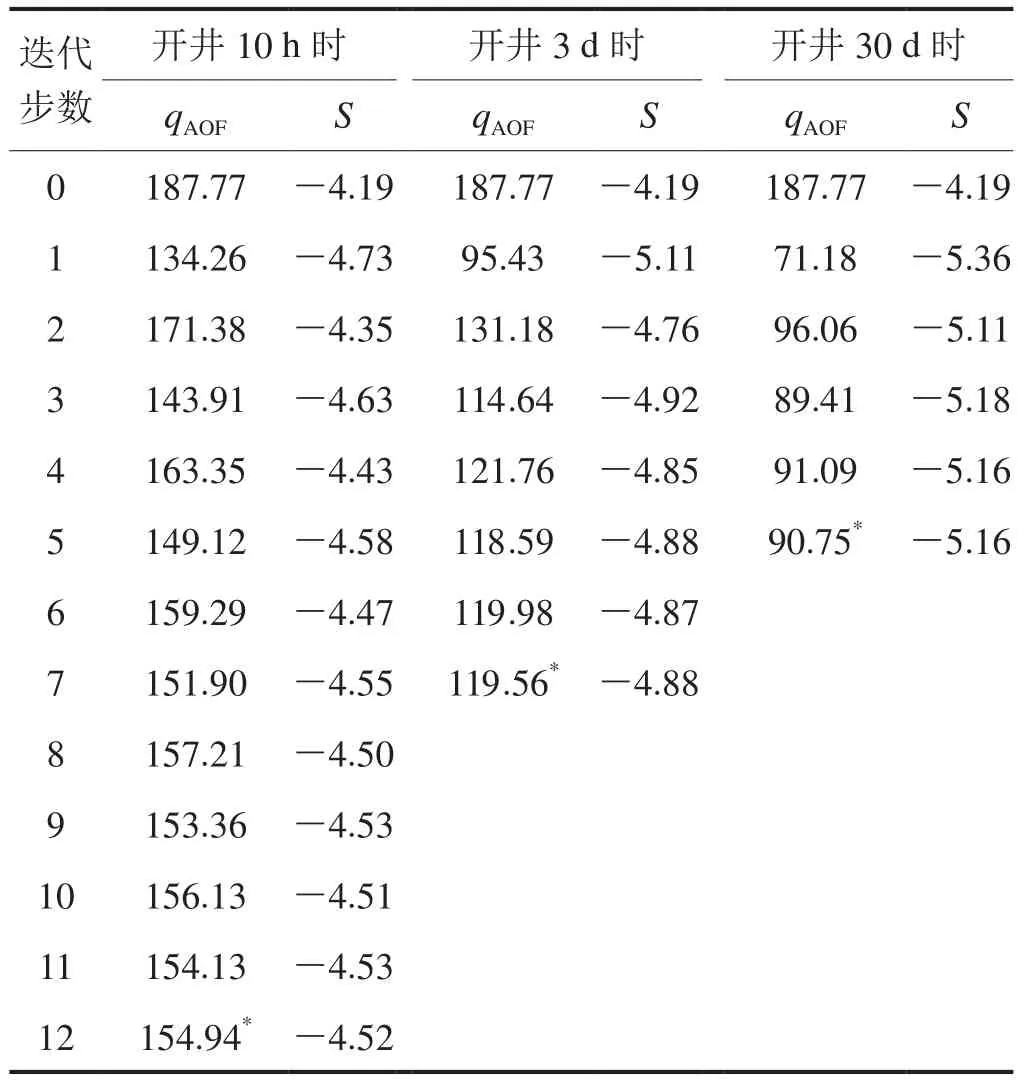
表4 预测GS1井qAOF变化特征的迭代计算数据表

笔者采用制作图版的原始数据手工计算，当qAOF稳定至整数部分的个位（四舍五入后）不变时，终止迭代；若采用查图版手工计算，可将S稳定至小数第一位（四舍五入后）不变作为迭代计算的终止条件。从表4数据看，时间越长迭代收敛越快；按上述第二种终止条件，查图版迭代计算大体不超过5次即可获得最终结果，该条件下qAOF计算值与按第一种迭代终止条件所计算的qAOF相比误差小于5%。

GS1井（灯二段为主产层）2012年9月投产后，配产介于5h104～10h104m3/d时生产较稳定；在试采过程中开展过气产量为35h104m3/d生产的试验，6天内气产量递减到12h104m3/d。该井近井区存在裂缝使得气井初期产能较高，远井区渗透率低则引起产能快速下降。表4中的最终计算结果简要描述了该井无阻流量的递减规律，可以看出，即使是试气期高产这种容易使人们对气井持续稳产能力产生经验性误判的情况，新方法仍然能准确预测产能不稳定本质特征，并且预测结果与后续生产情况相符。

6.4 新方法的其他应用示例

下面以近十余年四川盆地天然气开发热点区块的部分重点井为例，来验证新方法的应用效果。

图1中涉及的4口气井均是探井，且做过专项试井，有高质量压力恢复试井资料，以及稳定试井或修正等时试井资料。试井解释得到了对应于短时开井时刻的“稳定”qAOF，以及多个测试产量分别对应的S，由此计算了D，结果见表5。采用文中介绍的新方法另外计算D，并推算后续时刻的qAOF，表6定量揭示了稳产能力较强的气井不易被发现的产能递减特征及存在的差异，有助于深化气井产能评价的认识。

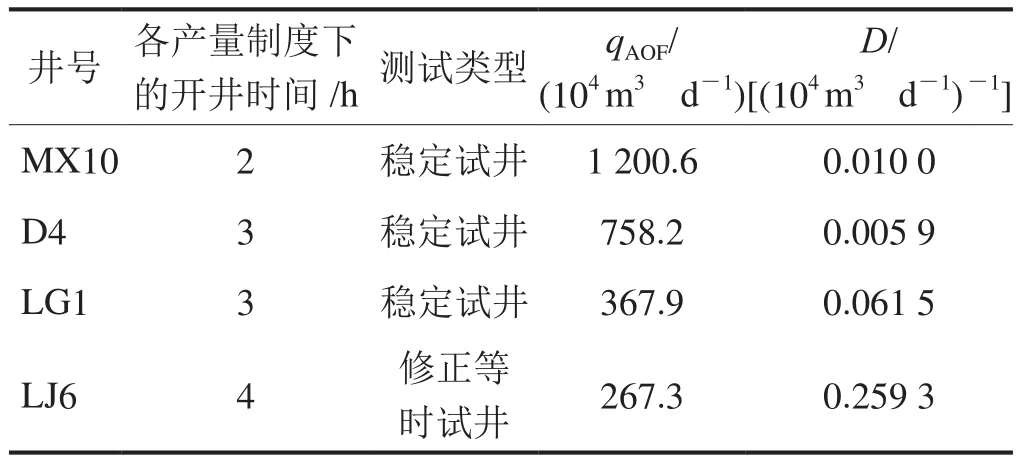
表5 四川盆地4口高产探井产能试井计算qAOF和D统计表

表6 四川盆地4口高产探井不同开井时间点qAOF预测数据表（新方法）

新方法为获取紊流效应影响下的非达西流动系数提供了新途径，在此基础上对比不同气井的非达西流动系数，能间接认识储层微观储集空间特征存在的差异。表5、6中数据显示新方法分析的非达西流动系数比试井解释结果略大，且产能越大的气井这种差异越明显。基于理论分析，结合部分气井产量增大后表皮系数与产量线性关系发生变化的实际情况，认为在远低于无阻流量的开井产量状态下试井，解释得到的非达西流动系数偏小。

采用新方法预测气井无阻流量的变化需要储层孔隙度和渗透率、流体黏度、综合压缩系数以及初期无阻流量参数值；另外需要净表皮系数、非达西流动系数二者之一。研究发现对一些高产气井而言，因在绝对无阻条件下紊流效应对其无阻流量的影响远远大于净表皮系数的影响。因此即使净表皮系数未知，无阻流量预测也相当准确（表7）。

表7 Sc误差较大情况下高产气井qAOF预测数据表

大多数新井试气时都未进行产能试井，应用新方法时通常需要依靠“一点法”提供参照基准。对于生产压差较小的气井，常规“一点法”误差较大，宜采用参数约束改进“一点法”[32]。

以上列举了测试资料较全的高产探井典型应用案例，另有部分探井及上试新层老井的分析实例如表8所示。新方法与传统方法配合，能够显著提高气井产能评价的质量，获得更丰富的认识，为天然气勘探与开发评价、产能建设可行性论证及气藏开发设计提供重要技术依据。

7 结论

1）获得均质储层平面径向流模型气井无阻流量随时间变化精确解，其适用范围拓展至径向流直线段出现之前。

2）确认表皮系数和地层导压系数是气井不稳定产能特征多样化的主要控制因素，分析揭示了其影响关系。

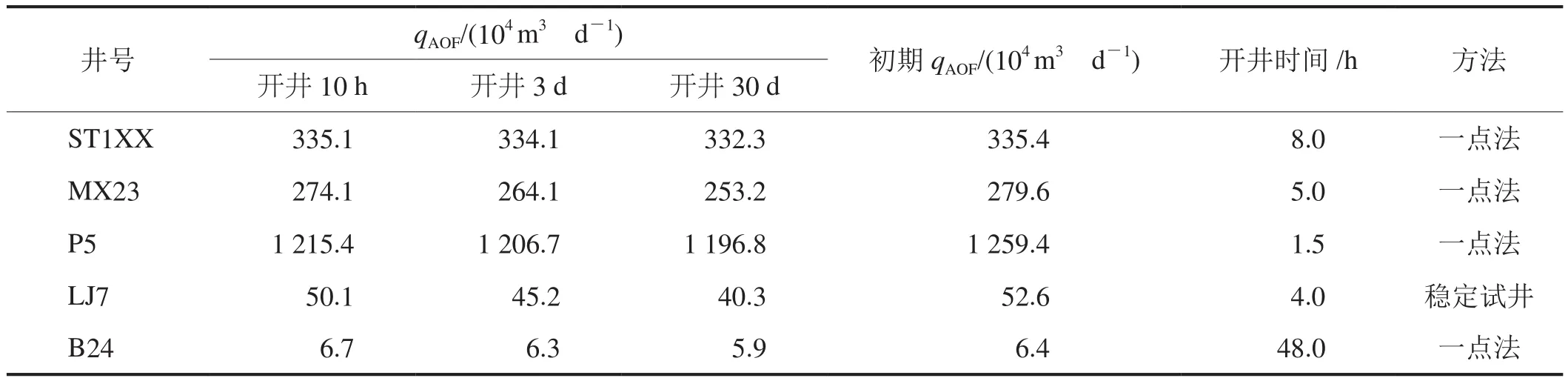
表8 四川盆地部分探井及上试新层气井qAOF预测数据表

3）形成气井不稳定产能非线性影响因子分析图版、无阻流量递减特征预测的迭代算法，达到实用化程度。

4）提出计算非达西流动系数新方法，既可用于分析气井不稳定产能，也可用于间接评价储层微观储集特征。

5）对于均质、视均质或与之相似储层中的直井，新方法分析准确，具有较强实用性。