基于DHGF算法的综合管廊出线节点选型研究
邓玉莲, 王俊岭, 张智贤, 魏 胜
(1. 北京建筑大学 北京未来城市设计高精尖创新中心, 北京 100044;2. 中国市政工程西北设计研究院有限公司, 甘肃 兰州 730000;3. 北京市市政工程设计研究总院, 北京 100082)
0 引言
城市综合管廊作为城市地下空间可持续发展的重要技术手段,在国外已有100多年的历史[1-3]。在我国的北京、上海、深圳、广州等地,综合管廊均已建成使用[4-5],但我国对于综合管廊各方面的研究仍处于起步阶段[6-7]。综合管廊的一些节点如监控中心与综合管廊的连接、综合管廊之间的丁字形及十字形节点,是综合管廊的重要部分,也是综合管廊的设计难点[8]。
本文主要针对综合管廊出线节点的选型问题展开研究。综合管廊出线节点形式一般分为上出线和下出线。两者在工艺上有很大的区别,上出线节点是在管廊标准仓上部加高和增设楼梯,满足管线衔接和人员通行,而下出线节点是在管廊下部增设夹层和钢爬梯,且上出线与下出线节点的防水、通风等工艺也有所不同[9]。与下出线相比,上出线节点工艺简单,施工难度低,结构受力小,因此需要投入的人工成本及材料费用较低,但上出线节点一般埋深较低,对覆土要求较高。当上出线不能满足管线的弯曲半径和避让关系时,需要采用下出线的形式。此外,对于管线类型较多,避让关系较复杂的工程,采用下出线有利于城市地下综合管线的管理与扩建,可以很好地解决马路拉链问题[9-10]。在实际建设中,综合管廊出线节点的选型要根据当地的水文地质、建设时序、规划红线、资金投入等各方面的指标进行综合选定,是一项极其复杂的系统工程。
目前,国内外学者对综合管廊的研究偏向于整体的设计规划和后期的运营维护。文献[11]利用德尔菲法和层次分析法建立起一套基于颜色编码的专家评判系统。文献[12]分析了综合管廊建设过程中的安全隐患,并基于旧城区建设管廊的经济条件,对布局规划给出了建议。牟秋等[13]建立了综合管廊建设需求的评价指标体系,并运用层次分析法研究了管廊的系统布局。还有一些学者针对综合管廊的重要节点做了初步研究,范翔[8]以南京某综合管廊实际工程为例,提出十字形交叉节点的设计原则和设计思路。高丽君[14]对综合管廊节点的断面设计、管线布置、人员通道及材料选择方面进行了分析。曾庆红[15]结合规范和国内外案例,对管廊交叉节点设计顺序和思路进行了系统归纳。
这些研究大部分都只是分析了管廊节点的整体设计方法,并没有深入分析出线节点的选型。我国综合管廊出线节点的选型一般是参照相关图集和案例进行,没有具体可行的标准。住建部于2015年5月22日发布的最新版《城市综合管廊工程技术规范》(GB 50838—2015)中只是对综合管廊节点的人行通道、通风及吊装口的设计做了简要说明,也没有涉及出线节点选型问题。本文利用DHGF算法建立综合管廊出线节点选型的数学模型,为解决综合管廊出线节点选型问题提供科学可行的理论方法。
1 理论基础
DHGF算法源自钱学森提出的从定性到定量的综合集成方法及顾基发提出的物理-事理-人理方法[16],是一种将改进的德尔菲法、层次分析法、灰色关联法和模糊数学判断4种方法的优势集于一身,将开放性和复杂性的信息先定性再定量的综合集成方法[17]。
DHGF算法的具体思想是建立DH模型,即指标体系中的因素采用改进的德尔菲法和专家讨论法,使原始的评分矩阵可用。德尔菲法的优点是从专家问卷中得到有用的信息,在评价矩阵的基础上,采用层次分析法确定评价指标的权重,将基于灰色关联理论和模糊评价理论的GF算法应用于评价指标体系的计算中,最后给出综合评价结果。
2 模型构建
2.1 利用德尔菲法构建评价体系
选定10位来自综合管廊不同专业领域的知名设计专家进行匿名调查问卷,列举综合管廊出线选型的影响因素,整个过程采用“统计—反馈”循环机制统一专家意见,同时采用“一票否决法”,即只要有1位专家对拟定的某一指标持否定态度,就将其排除。通过分析专家意见得出最终的指标集
Ci={C1,C2,…,Cn}。
(1)
根据统计结果进行指标分析整合,最终得到3个一级指标,12个二级指标并建立递阶层次评价体系,如图1所示。评价体系分为4个层级: 目标层A、一级指标层B、二级指标层C和方案层D。

图1 综合管廊出线选型评价体系
2.1.1 指标影响分析
2.1.1.1 技术条件指标
技术条件指标包括水文地质、施工难度、运营维护和气候条件4个二级指标。水文地质对管廊的设计与施工会造成一定的影响,如管廊所在的地质层构造与岩土结构将直接影响管廊的结构稳定性[18],地下水位、土质的疏松度和酸碱度也会影响管廊节点的防水设计等。
施工难度受工艺结构的复杂程度和施工技术条件的影响,且这些直接决定工程的建设工期。在综合管廊出线节点设计中,下出线节点的工艺比较复杂。为了满足综合管廊后期的改扩建与运营维护需求,一般要在管廊中预留人行通道和爬梯,以方便工作人员进入管廊开展检修工作。管线的出线节点设计不但要满足管线转弯半径的需求,还要使得维修通道平滑接入管廊标准段[19]。
综合管廊一般采用明渠开挖的方式,且建设工期较长,当地的气候条件可能会对管廊的施工进程造成一定的影响。如果当地降雨较多,会对管廊的防水设施要求较高。下出线节点采用顶管施工能在一定程度上降低降雨对施工的影响。
2.1.1.2 出线条件指标
出线条件指标包括管廊覆土、建设时序、管线规模和管线种类4个二级指标。由于地面荷载和冻土的影响,综合管廊的建设一般对覆土厚度有一定的要求。沿道路敷设的综合管廊,其覆土厚度直接影响工程投资及道路的路面质量,当覆土较浅时其台背回填处理措施应着重设计[20]。在综合管廊的建设中,会不可避免地与地铁、地下通道等地下工程共线、交叉等[21],新建项目要与已建或计划要建的项目保持一定的安全距离,一般遵循支线避让干线,新建避让已建的原则。管线的规模直接决定了管廊出线节点的规模,管廊空间的大小、通风性能及夹层设计尺寸必须充分考虑管线弯曲半径、电力电缆分层、管线数量与间距等因素[19]。不同类型的管线布置在一起,很容易产生干扰,如电力电缆与热力管线、电力与燃气管线等之间易发生爆炸或火灾等危险[9, 22]。
2.1.1.3 适用条件指标
适用条件指标包括规划红线、地表构筑物密度、结构受力和资金投入4个二级指标。综合管廊的设计与建设,必须根据当地城市的规划现状来确定。规划红线是根据有关政策及勘测结果总结出来的,一般不可更改。地表构筑物会影响管廊结构的受力情况,而且在一些大型商场及居民区都建有地下停车场或地下通道,这就使得综合管廊的路线选择更加困难。此外,不同形式的出线节点,其防火、防水、通风的空间尺寸存在较大的差异。下出线节点除了要承受地面荷载和节点自重,还要承载管廊标准段的荷载。地下综合管廊所用的材料一般为钢筋混凝土,2种出线节点工艺不同,结构受力不同,施工程序不同,因此所需要的材料费用和人工成本也有所差异。
2.1.2 指标分值转换
二级指标层的12个指标,实际上是12个影响因素,这些因素对管廊建设具有重要作用,有些指标值越小越好,有些指标最佳值在某个特定区间,有些指标值则越大越好。为解决衡量标准不一的问题,将各指标分为成本型指标、区间型指标和效益型指标,并通过无量纲方法对各类指标进行转换[23]。
1)成本型指标转换公式
(2)
式中:vij为专家j对指标i的评价值隶属度;aij为原始评价值;aj max和aj min为某二级指标Ci的最大和最小评价值。
2)区间型指标转换公式
(3)
式中[S1,S2]为Ci的最佳区间。
3)效益型指标转换公式
(4)
2.2 利用层次分析法计算指标权重
邀请专家参照Saaty的1—9标度法[24](见表1),通过定量判断不同指标之间的相对重要性关系进行填写,构建城市综合管廊出线选型的评价指标表。

表1 标度分级及含义
采用和积法处理收集到的专家评价数据,计算方法是先将判断矩阵A的n个行向量按照行归一化,然后将归一化的行向量求和,将相加的向量除以判断矩阵阶数n取平均值,即可得到权重向量[25]。和积法优势在于相对简单可靠,易于理解,受个别值的影响较小。和积法计算判断矩阵特征值与特征向量的计算步骤为:
1)将判断矩阵A按列向量进行归一化处理,处理后矩阵第i行j列的元素为bij
(5)
2)将列向量归一化后得到的矩阵B中的元素按照行求和,可以得到向量C=(c1,c2,…,cn)T。
(6)
3)对向量C进行归一化处理得到特征向量W=(W1,W2,…,Wn)T,其中
(7)
4)计算最大特征根的近似值
(8)
由于层次分析法受主观因素影响较强,可能导致判断信息与实际相差甚远,因此需要对判断矩阵进行一致性检验,检验公式如式(9)—(10)所示。当一致性比率(consistency ratio,简称CR)<0.1时,即认为构造的判断矩阵通过了一致性检验,否则需调整判断矩阵。
(9)
式中: CI为一致性指标;λ为判断矩阵的特征根;n为判断矩阵阶数。
(10)
式中: CR为一致性比率; RI为随机一致性指标。
RI随判断矩阵的阶数变化见表2。

表2 随机一致性指标变化表
邀请专家分别基于实际设计过程中遇到的综合管廊出线选型问题对一级指标和各二级指标进行评价。以某一级指标为例,对形成的判断矩阵进行计算和一致性检验后,得出各一级指标的权重分别为W1、W2和W3,如表3所示。

表3 一级指标权重计算表
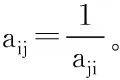
重复上述步骤对12个二级指标分别进行评价和处理,并乘以相应的一级指标权重,可以得到各二级指标Ci上的模糊权重子集:
(11)
2.3 利用灰色关联法计算灰色评估权值和权矩阵
2.3.1 确定样本矩阵及评价等级
采用专家打分的形式对决定综合管廊出线选型的12个评价指标进行二次评价,规定专家打分范围为1~10。基于测度理论,将评价结果划分为优、良、中、差4个等级。按10分打分制,设立综合评价等级集合为:
V={V1,V2,V3,V4}={9,7,5,2}。
(12)
2.3.2 确定灰数的灰度
评价值的大小代表了专家根据经验对某一指标的重要性判断,但不能精确地表达指标的重要性程度。可以将评价值理解为只知其取值范围,不知其确切值,因此是一种灰数。评价等级将灰数分成了优、良、中、差共4类,据此可以建立可能度函数并根据设立的评价等级将可能度函数分为4类,从而将关于管廊出线选型的灰色信息代入其中进行处理,进而对评价值的灰度进行精确表示。
1)第1类,优级可能度函数,设定灰数∈[9,∞)
(13)
2)第2类,良级可能度函数,设定灰数∈[0,7,14]
(14)
3)第3类,中级可能度函数,设定灰数∈[0,5,10]
(15)
4)第4类,差级可能度函数,设定灰数∈[0,2,4]
(16)
2.3.3 计算灰色统计数
将10位专家对各指标的评价值分别代入4类可能度函数,求出各指标属于各可能度函数的灰色统计数nij和总灰类统计数nt。
以二级指标C1(水文地质)为例,设10位专家对水文地质影响出线形式的评价值为c11,c12,c13,c14,c15,c16,c17,c18,c19,c110,则C1属于各级可能度函数的灰色统计数为
优: n11=f1(c11)+f1(c12)+…+f1(c110);
(17)
良: n12=f2(c11)+f2(c12)+…+f2(c110);
(18)
中: n13=f3(c11)+f3(c12)+…+f3(c110);
(19)
差: n14=f4(c11)+f4(c12)+…+f4(c110)。
(20)
因此,可求得总灰色统计数nt=n11+n12+n13+n14。
2.3.4 确定灰色权矩阵
10位专家对二级指标C1(水文地质)的灰色评估权值分别为
(21)
同理求得其他二级指标的灰色评估权值rij(i=1,2,…,12; j=1,2,3,4)。可得属于各二级指标的灰色权矩阵
(22)
2.4 利用模糊数学判断方法计算评价结果
用层次分析法获得的权重矩阵W分别与不同方案的各二级指标灰色权矩阵R1、R2相乘,得到模糊判断矩阵F1、F2。再用之前设定的综合评价等级以向量的形式分别与模糊判断矩阵F1、F2相乘,得到2个方案的评价得分Z1、Z2。通过比较评价结果选择评价值最高的方案为最优方案。计算方法如下:
F1=W×R1=[f1f2f3f4];
(23)
F2=W×R2=[f5f6f7f8];
(24)
Z1=V×F1=(9 7 5 2)×[f1f2f3f4]T;
(25)
Z2=V×F2=(9 7 5 2)×[f5f6f7f8]T。
(26)
3 实例研究
北京某综合管廊项目总长为1 551 m,位于北京市中心,属于老城区的新建综合管廊项目,包括新建总长为1 256 m的主管廊和总长为195 m的支管廊,工程总平面如图2所示。
以实兴东街道路下综合管廊为例,该管廊共有地块分支节点5处,路口分支节点1处以及端部出线节点2处。该路口分支节点为与石景山北1区二号路综合管廊的交叉节点,其中实兴东街处综合管廊为南北走向,位于北1区二号路综合管廊的上方。现将综合管廊工程中的该交叉节点设计及施工现状代入管廊出线选型模型进行验证。
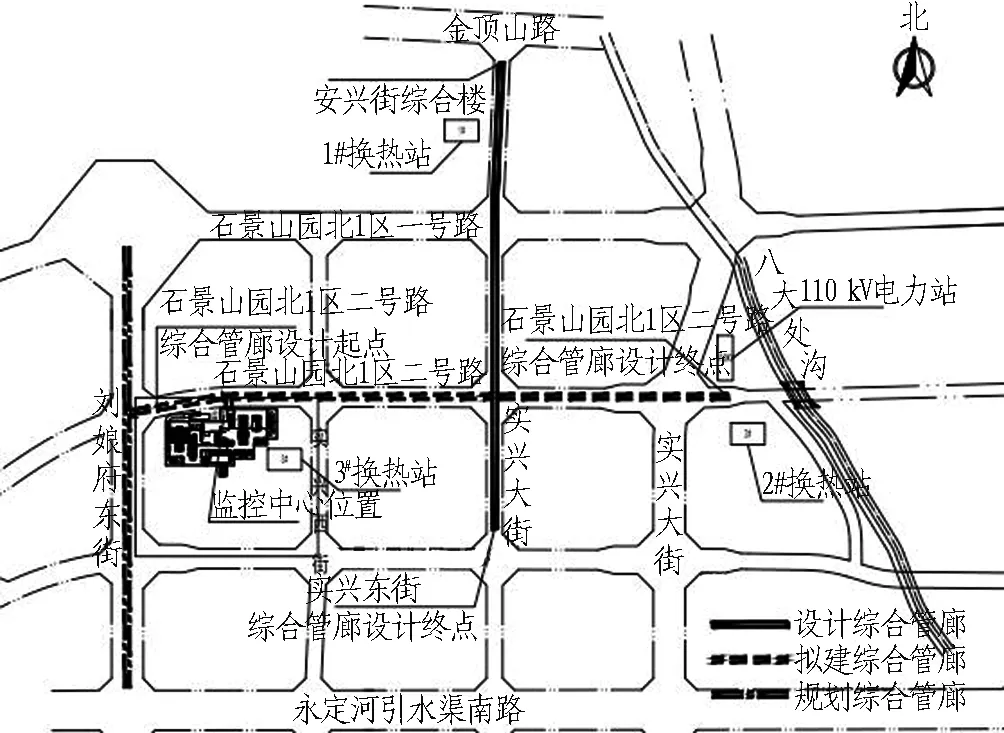
图2 综合管廊工程总平面图
3.1 利用层次分析法计算指标权重
为了获得准确的指标相对重要性标度,特邀请综合管廊安全示范工程课题组内6位具有管廊施工、设计及科研经验的综合管廊专家对唯一一处路口交叉节点进行现场勘察分析,然后对3个一级指标和12个二级指标参照1—9标度法进行评定。再将得到的准则层二级指标权重和与之对应的一级指标的权重相乘,即可得到水文地质(C1)、施工难度(C2)、运行维护(C3)、气候条件(C4)、管廊覆土(C5)、建设时序(C6)、管线规模(C7)、管线类型(C8)、规划红线(C9)、地表构筑物密度(C10)、结构受力(C11)以及资金投入(C12)这12个评价指标在整个评价指标体系中的权重,分别为WT={0.012,0.030,0.066,0.012,0.147,0.090,0.051,0.032,0.280,0.157,0.045,0.078}。
3.2 利用灰色关联分析法计算灰色权值
邀请来自综合管廊设计领域的不同专业(建筑、结构、市政、概算和规划专业)的设计专家共10名,对决定综合管廊上出线与下出线选型的12个评价指标分别进行评价(打分范围为1~10分),结果如表4和表5所示。
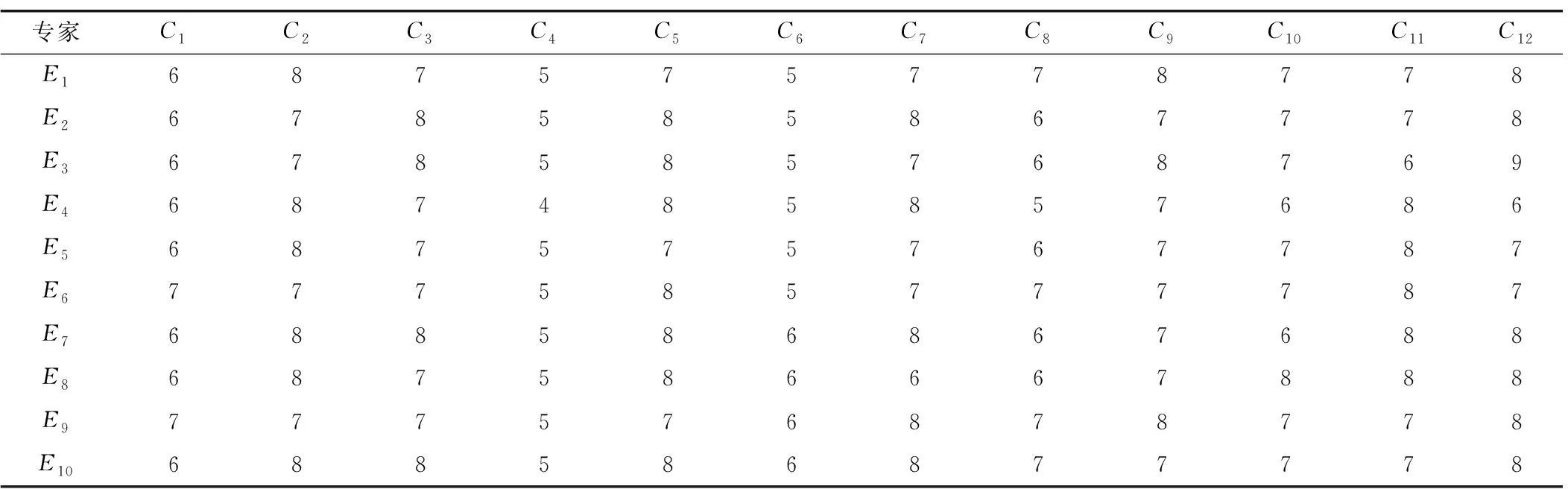
表4 某综合管廊(实兴东街)上出线评价表

表5 某综合管廊(实兴东街)下出线评价表
根据可能度函数算法,并结合式(17)—(21),计算2种出线方案的各12项二级指标的灰色统计数,并按式(22)确定灰色权值并构建权矩阵,结果如下(R1为上出线方案的权矩阵,R2为下出线方案的权矩阵)。
3.3 计算评价结果
用层次分析法获得的权重矩阵W分别与上、下出线节点方案中各二级指标的灰色权矩阵R1、R2相乘,得到模糊判断矩阵F1、F2。
F1=W×R1=(0.345 0.404 0.251 0);
F2=W×R2=(0.372 0.409 0.219 0)。
再用之前设定的综合评价等级以向量的形式分别与模糊判断矩阵F1、F2相乘,得到2个方案的评价得分Z1、Z2。
Z1=F1×VT=(0.345 0.404 0.251 0)×(9 7 5 2)T=7.188;
Z2=F2×VT=(0.372 0.389 0.239 0)×(9 7 5 2)T=7.266。
通过比较评价结果,发现2个方案的评分等级都为良,且评价值较高的方案为下出线方案(7.266)。事实上,利用四元集成法建立的管廊出线选型评价模型得出的最终结果与某综合管廊(实兴东街)工程规划设计前期的专家论证结果是一致的。
此工程实例验证了基于GHDF算法建立的综合管廊出线节点选型模型的可靠性和可操作性。在解决实际工程问题时,可以适当的采取此种方法,将影响某管廊工程出线节点选型的各种主观因素进行量化分析,帮助管廊节点选型决策 。
4 结论与讨论
本文将DHGF算法应用到综合管廊出线节点的选型中,建立了出线节点的选型模型,并通过实例应用,验证了此评价方法的可行性,为综合管廊出线节点的选型提供了系统的评价方法。但由于综合管廊出线节点选型所涉及的影响因素错综复杂,且影响因子的遴选及指标重要度评定都受人为因素的影响,主观性较强,并不能完全符合实际情况。在以后的研究及应用中,应注重基础数据的收集与完善,逐步扩大指标评定构架,使得评价结果更精准可靠。此外,本文所建立的选型模型作为综合管廊出线节点选型的一种方法,虽然经过了实例验证,但缺少与其他方法计算结果的对比,后续可以探讨使用不同的方法来进行对比分析。

