用高压气体吸脱附-微量热联用法对CO2和CH4在煤上吸附热力学的研究*

李龙建 张 雷 郭建英 刘生玉 张素红

(太原理工大学矿业工程学院，030024 太原)

0 引 言

温室气体的排放引发了全球变暖，CO2作为最主要的温室气体，减少其排放量已刻不容缓[1]。煤层气作为一种高效、环保、储量丰富的能源，近年来受到人们的广泛关注[2]。由于CO2和CH4在煤层中存在竞争性吸附，CO2分子与煤分子之间作用力强于CH4与煤分子之间的作用力，因此CO2可以取代煤层中吸附的甲烷，有利于从煤层中回收甲烷进而控制CO2的排放[3-7]。目前，国内外学者主要通过实验获取CO2和CH4在煤上的吸附等温线来计算吸附热。杨峰等[8]利用修正Langmuir吸附模型计算甲烷在页岩上的等量吸附热为14.58 kJ/mol，极限吸附热为23.91 kJ/mol。白建平等[9]利用克劳修斯-克拉贝龙方程计算出甲烷在无烟煤上的等量吸附热和极限吸附热分别为23.31 kJ/mol和24.02 kJ/mol。相建华等[10]通过分子模拟研究，得出CO2的吸附量及等量吸附热均大于CH4的吸附量及等量吸附热。降文萍等[11]则通过研究煤表面CH4和CO2分子间作用能，从微观角度证实煤体对CO2吸附能力更强。林海飞等[12]认为CO2的吸附势能、吸附热和吸附熵变均大于CH4的吸附势能吸附热和吸附熵变。迄今为止，文献[13-16]利用吸附等温线来计算有关CO2和CH4在煤上的吸附热的方法较多，没有一个较统一的基准来比较两者之间的差异性则容易带来争议，而通过实验直接测定吸附热来比较两者吸附特性差异则更为准确。

笔者通过测量C1O2和CH4在不同温度下的吸附量，从而确定其吸附模型，计算出等量吸附热和极限吸附热；再利用高压气体吸脱附-微量热联用仪测出其吸附热。理论计算与实验相结合来研究CO2和CH4热力学机制，从热力学的角度揭示CO2和CH4竞争性吸附机理，为驱替理论提供热力学参考。

1 实验部分

1.1 实验样品

实验选用山西大同弱黏煤作为实验煤样，通过破碎筛分选取粒度为0.074 mm以下的煤样。将煤样放置于真空干燥箱中烘干，设置温度为100 ℃，干燥10 h，直到样品质量不发生变化。根据GB/T 212-2008对弱黏煤进行工业分析和元素分析，结果如表1所示。

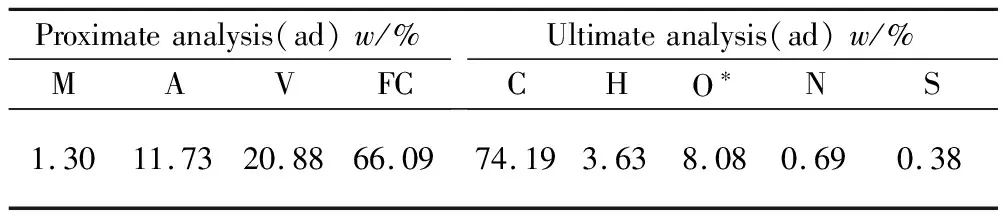
表1 煤样的工业分析和元素分析

* By difference.

1.2 实验仪器及气体

高压气体吸脱附仪：法国塞塔拉姆公司研发的全自动高温高压吸脱附仪(PCT)，该仪器采用静态容量法原理测量吸附量[17]。实验装置由高压储气罐样品池(0 MPa～20 MPa)，全自动PID控制气压，5种不同的已校准蓄气池，温度调节处理系统(0 ℃～400 ℃)，计算机控制的全自动软件，高灵敏度可燃性气体检测传感器组成。

微量热仪：采用的C80型微量热仪为法国塞塔拉姆公司基于卡尔维式原理设计的一种新的热量测量仪器，能够精准测量实验过程中热量的微量变化。高压气体吸脱附-微量热联用仪装置见图1。

气源：由山西铜盾贸易有限公司气体部提供的高纯氮(99.999%)作为气动阀门，高纯氦气(99.999%)来标定体积，二氧化碳(99.95%)和北京北氧联合气体有限公司提供的纯甲烷(99.99%)作为实验气体。

1.3 吸附实验

利用高压气体吸脱附仪来测量吸附量。实验过程由真空脱气、标定体积、测量PCT三部分组成。在温度80 ℃下抽真空6 h，用氦气分别在常温和实验温度下标定样品池体积，在温度为30 ℃，40 ℃，50 ℃，压力为0 MPa～2 MPa条件下进行等温吸附实验，获得不同温度下CO2和CH4的吸附量。

图1 高压气体吸脱附-微量热联用仪装置

1.4 吸附热实验

通过高压气体吸脱附仪-微量热仪联用来测量吸附热。实验过程包括真空脱气、标定体积、测量吸附热三个阶段，在30 ℃下抽真空6 h，用氦气分别在常温和实验温度标定样品池体积，在温度为30 ℃，40 ℃，50 ℃，压力为0 MPa～2 MPa条件下测量CO2和CH4在煤上的吸附热。

2 CO2和CH4吸附热力学模型

2.1 吸附模型

煤对CO2和CH4吸附模型采用Langmuir模型和Freundlich模型来拟合。Langmuir吸附模型表示吸附为单分子层的物理吸附，被吸附在固体表面的分子间无相互作用，吸附平衡为动态平衡。其方程如下[18]：

(1)

式中：V表示吸附量，mmol/g；a表示Langmuir常数，物理意义为煤对气体的最大吸附量，mmol/g；b表示Langmuir压力常数，MPa-1；p表示平衡压力，MPa。

Freundlich方程是经验公式，其公式参数没有明确的物理意义，但却依然能够揭示部分实验现象。其方程如下[19]：

V=Kapn

(2)

式中：V表示煤对气体的吸附量，mmol/g；p表示气体压力，MPa；Ka为吸附平衡常数，与吸附剂和温度有关；n为常数且小于1，与温度有关。

2.2 等量吸附热计算模型

吸附热不仅可以反映出气体吸附类型，还可以更加直观地反映出煤对气体的吸附程度，是评判吸附强弱的重要手段。

等量吸附热表示吸附量一定时，再有无限小的气体被吸附时释放出的热量。精确测量等量吸附热较为困难，一般都通过将实验测得的吸附等温线转换成等量吸附线，再利用克劳修斯-克拉贝龙方程来计算出等量吸附热。具体方程如下[8-9]：

(3)

式中：p表示平衡压力，MPa：T为绝对温度，K；R为气体常数，取8.314 J/(K·mol)；Q为等量吸附热，kJ/mol。

2.3 极限吸附热计算模型

极限吸附热是指当平衡压力趋于零时的吸附热，能够直接反映煤分子与气体之间的相互作用力，通常利用范特霍夫方程来计算。具体形式如下[20]：

(4)

式中：K表示Henry常数；ΔH为极限吸附热；T，Q，R与方程(3)中一致。

3 结果与讨论

3.1 CO2和CH4在煤上的吸附等温线

在温度为30 ℃，40 ℃，50 ℃条件下，CO2和CH4吸附等温线如图2所示。IUPAC协会将吸附等温线分为六种模型[21]，由图2可知，CO2和CH4在煤上的吸附等温线均属于Ⅰ型吸附等温线，且在同一温度下，吸附量随压力的增大先增大后趋于平缓。上述分析结果与杨峰等[8]的研究结果相符。在同一压力下，吸附量随温度的升高而降低，这是由于吸附是一个动态的过程，温度升高使吸附相中的气相分子获得更多的能量从而克服吸附力返回气相中，导致煤体的吸附量降低，同时也表明CO2和CH4吸附是一个放热过程。在相同温度和压力下，CO2在煤上的吸附量大于CH4的吸附量，表明CO2更容易吸附于煤表面。

图2 不同温度下煤对CO2和CH4的吸附等温线

将实验获得的吸附等温线利用Langmuir方程拟合，结果如表2所示。由表2可看出，随着温度的增大，a值逐渐减小，且相同条件下CO2的a值明显高于CH4的a值，这与吸附等温线所得结果一致。使用Freundlich方程对吸附等温线进行拟合，结果如表3所示。由表3可知，从R2可以看出其拟合效果不如Langmuir方程拟合效果好，所以后期等量吸附热的计算使用Langmuir模型。

表2 Langmuir拟合参数

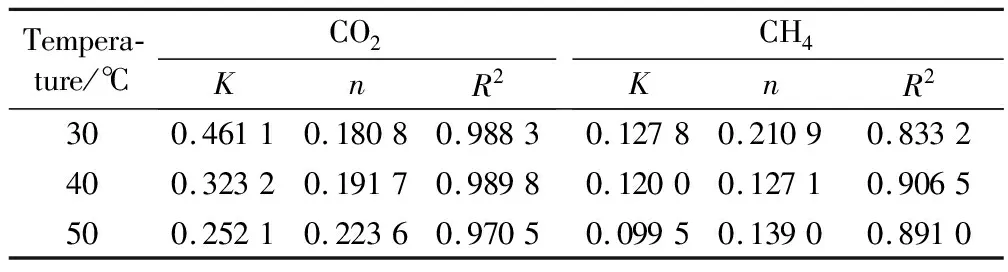
表3 Freundlich拟合参数

3.2 CO2和CH4在煤上的等量吸附热

将上述实验中所得到的煤对CO2和CH4吸附等温线通过Langmuir模型转化成等量吸附线，计算出不同吸附量下所对应的lnp与T-1，并进行线性拟合，结果如图3所示。

图3 CO2和CH4等量吸附线

由直线斜率得出不同吸附量下所对应的等量吸附热如表4和表5所示。由表4可知，CO2在煤上的等量吸附热为34.76 kJ/mol～44.83 kJ/mol，平均为39.27 kJ/mol，表明煤吸附CO2的过程为物理吸附。CH4在煤上的等量吸附热为20.79 kJ/mol～32.86 kJ/mol，平均为26.41 kJ/mol，小于CO2等量吸附热，同时也反映煤吸附CH4的过程为物理吸附。当吸附量同为0.1 mmol/g时，CO2在煤上的等量吸附热为36.59 kJ/mol，CH4在煤上的等量吸附热为20.79 kJ/mol，CO2在煤上的等量吸附热高于CH4，表明CO2分子与煤分子之间作用力强于CH4与煤分子之间的作用力，且分析结果与王向浩等[5]的研究结果一致。

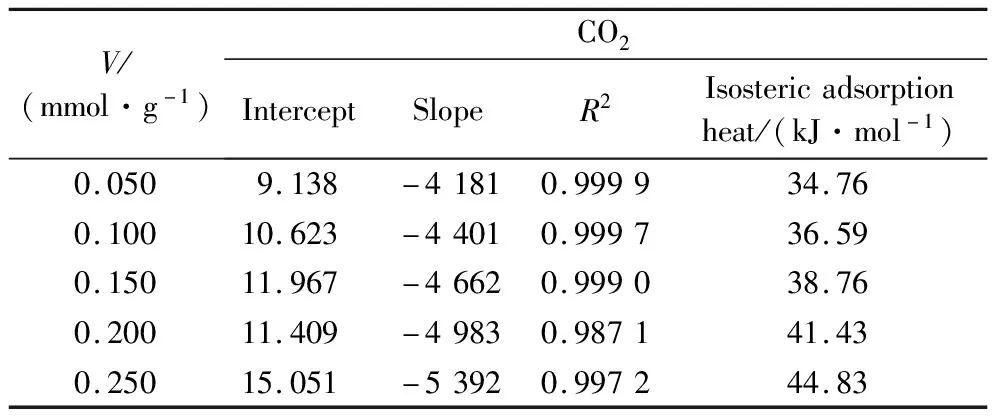
表4 CO2等量吸附线性拟合结果及等量吸附热

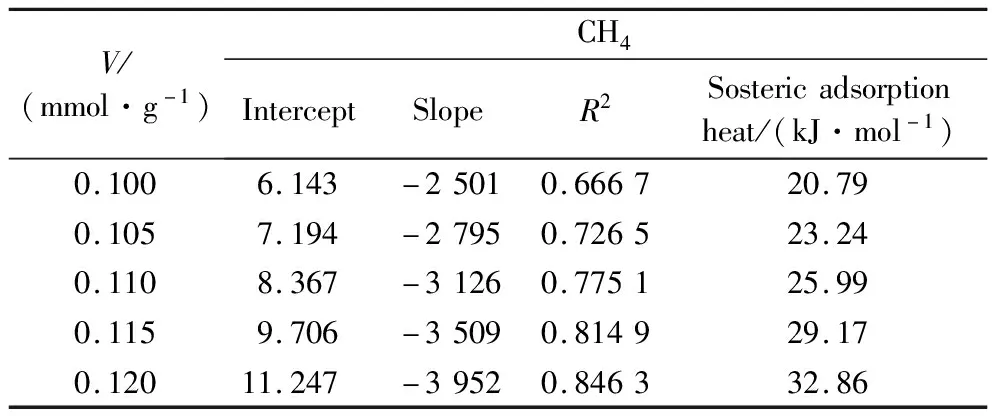
表5 CH4的等量吸附线性拟合结果及等量吸附热

等量吸附热随吸附量的变化主要与两方面的因素有关。一方面是由于固体表面的不均匀性，气相分子优先吸附煤样中高能量的吸附位，导致等量吸附热随吸附量的增大而减小；另一方面是由于吸附相内被吸附分子之间的作用力随着吸附量的增大而逐渐增强，导致吸附热增大[12]。由表4和表5可知，CO2和CH4的等量吸附热都随吸附量的增大而增大，根据以上分析可知，出现这种现象是由于随着吸附量的增大，吸附质分子之间的作用力增强。

3.3 CO2和CH4在煤上的极限吸附热

极限吸附热能直接反映吸附质分子与吸附剂分子之间的作用力。图4所示为CO2和CH4在煤上吸附的lnK对T-1的关系曲线。表6所示为相关拟合参数值与极限吸附热值。由表6可知，CO2和CH4的极限吸附热分别为54.02 kJ/mol和19.68 kJ/mol，表明CO2极限吸附热远大于CH4的极限吸附热，说明CO2与煤分子之间的作用力大于CH4与煤分子间的作用力，与上述等量吸附热和已有的研究结果[10-11]相一致。

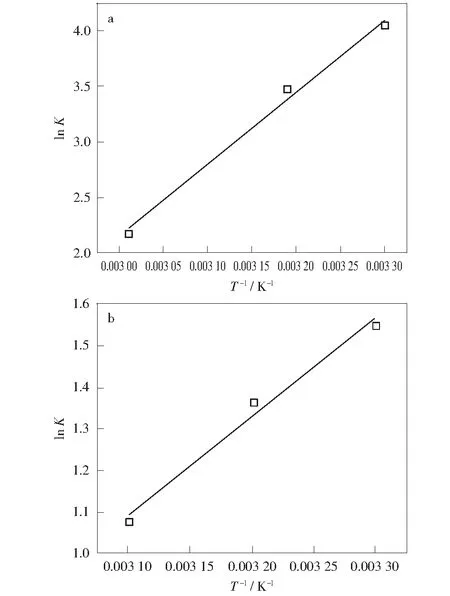
图4 CO2和CH4在煤上吸附的ln K对T-1的关系曲线及线性拟合

表6 CO2和CH4的ln K对T-1拟合结果及极限吸附热

3.4 CO2和CH4在煤上的吸附热

等量吸附热和极限吸附热都是利用实验得到的吸附等温线通过理论计算得到，而通过微量热仪和高压气体吸脱附仪联用可得到实验状态下的吸附热，理论计算与实验相结合更加具有说服力。图5所示为30 ℃下弱黏煤对CO2和CH4的吸附热流曲线(因其他温度的热流曲线与30 ℃的热流曲线相似，所以只提供30 ℃下的热流曲线)。CO2和CH4在各个温度下的吸附热值列于表7。由表7可知，同等温度下CO2的吸附热值约为CH4吸附热值的3倍，从实验角度也可以得出CO2分子与煤分子的作用力强于CH4与煤分子之间的作用力，与理论计算结果一致。

图5 30 ℃下CO2和CH4在煤上的吸附热

表7 CO2和CH4在不同温度下的吸附热

4 结 论

1)在实验压力范围内，CO2和CH4吸附等温线均属于Ⅰ型吸附等温线，且更符合Langmuir吸附模型。CO2和CH4在煤上的等量吸附热分别为39.27 kJ/mol和26.41 kJ/mol，CO2等量吸附热明显高于CH4等量吸附热，同时反映出煤吸附CO2和CH4的过程均为物理吸附。

2)CO2和CH4的极限吸附热分别为54.02 kJ/mol和19.68 kJ/mol，CO2极限吸附热约为CH4极限吸附热的2.6倍，表明CO2分子与煤分子之间的作用力强于CH4分子间与煤分子间的作用力。根据实验测出的吸附热可以看出，3种温度下CO2的吸附热都约为CH4的3倍，与计算结果一致。