915 nm宽条形半导体激光器输出特性

么 娜， 薄报学， 刘荣战， 徐雨萌， 高 欣

(长春理工大学 高功率半导体激光国家重点实验室， 吉林 长春 130022)

1 引 言

近年来，由于具有较好的输出光束质量以及转换效率高、工作稳定、结构小巧且耐用等优点，采用半导体激光器作为泵浦源的光纤激光器得到了较为广泛的应用。基于泵浦源在整个激光器中的核心位置，对于整个激光器器件而言，无论是工作效率还是使用寿命等，均受制于其所产生的影响，这最终会波及到激光器输出光束的质量[1]。0.9 μm附近波段的半导体激光器，经常被作为光纤激光器的泵浦源来使用，而915 nm这一波长在泵浦效率等方面具有一定的优势[2-4]，所以对其进行研究是具有现实意义的。当半导体激光器的输出光功率不断提升时，温度升高对激光芯片的性能所产生的不良影响也将愈加严重[5]，造成电光转换效率降低、阈值电流密度升高、输出光的谱线红移、出现多模式振荡等，甚至会使芯片的内部产生缺陷从而缩短激光器的使用寿命，影响了其在实际应用中的性能表现[6-11]。不仅如此，输出功率增大的同时会使得器件的温度分布更加不均匀，致使其慢轴方向出现明显的热透镜效应，进而导致其发散角增大，光束质量降低[12]。因此，国内外对这一问题开展了广泛的研究。2018年，张晓磊[13]分析了温升对半导体激光器阈值电流、输出功率、转换效率等特性的影响，并对其进行了模拟、优化；同一年，宋健等[14]采用仿真模拟的方式，对975 nm输出波长的半导体激光器进行了研究，评估了其等效的热透镜效应，并得出相同条件下热透镜焦距与热功率近似为反比关系，与慢轴光束发散角近似为线性关系，通过实验获得了慢轴发散角与注入电流之间的关系。2019年，赵碧瑶等[15]为了削弱808 nm波长半导体激光器因温度分布不均引起的热透镜效应，提出了一种特殊的封装构造，这种构造对芯片的边缘进行了绝热处理，通过使用计算机软件对该构造的半导体激光芯片进行模拟，结果显示与传统结构的器件相比，新型激光器在慢轴发散角方面缩小了28%。国外方面，2006年，Kemp等[16]利用有限元软件分析了垂直腔半导体激光器的热透镜效应对芯片性能的影响，并进行实验验证，研究了其对斜率效率、阈值电流和输出功率的影响。综上所述，国内外在半导体激光器的热透镜效应方面有一定研究，而对于具有重要应用价值的915 nm高功率半导体激光器的热透镜效应的研究较为少见。

2 半导体激光器的产热机制以及温升对其输出特性影响的相关理论阐述

2.1 半导体激光器的一般产热机制

半导体激光器工作时所产生的热量一般源自两方面：一是非辐射复合和波导光吸收等能量损耗所产生的热量；二是材料本身以及欧姆接触层电阻所产生的焦耳热，其表达式为[17-18]：

Q=j2ρ,

(1)

其中，Q为产生焦耳热的功率密度，j为电流密度，ρ为材料平均体电阻率。

2.2 温升对激光器输出特性的影响

2.2.1 温升对阈值电流的影响

一般地，半导体激光器的阈值电流密度与温度之间的关系可用公式(2)表示：

(2)

其中，Tr为一定温度，ΔT为相对温升，Jth(Tr)为对应温度的阈值电流密度，T0为特征温度。温升使芯片内部对载流子的限制能力变弱，所产生的漏电流使其内量子效率变低进而造成器件的阈值电流密度增大[19]。

2.2.2 温升对输出功率的影响

半导体激光器的输出光功率和驱动电流之间存在如下关系：

(3)

其中，P为输出光功率，I为驱动电流，Pth为器件在阈值电流注入状态下自发辐射所产生的光功率，Ith为阈值电流，ηex为外微分量子效率，Ep为光子能量，e为电子电荷。由于Ep、e为常数，Pth可忽略不计，因此输出光功率主要由I、Ith以及ηex所决定，并主要随有源区的温度升高而降低。输出功率的减小会使注入的电能更多地转变为热，从而产生进一步的温升，这构成了恶性循环，使激光器的输出功率饱和、更为快速地下降[20]。

2.2.3 温升对光谱特性的影响

半导体激光器的输出光波长会随有源区温度升高而发生红移，公式(4)描述了输出光波长与温度之间的关系[21-22]：

(4)

其中，h为普朗克常数，c为真空中的光速，Eg为有源层材料禁带宽度。在一定温度范围内，dEg/dT可认为是常量。

2.2.4 半导体激光器远场发散角受温度的影响

半导体激光器芯片的局部温升使材料介电常数发生改变，从而改变折射率分布，光经过时会发生不同程度的折射，类似于通过光学透镜所产生的汇聚或发散效应，即热透镜效应。当材料折射率呈现钟形分布时，可等效为自聚焦透镜[23-25]，孔径近似为激光器慢轴发散角增加量，如图1所示。

图1 自聚焦透镜

宽条形半导体激光器慢轴方向的侧向折射率分布受温度与载流子浓度分布等因素影响，通过公式(5)表示[14]：

(5)

其中，Δn为折射率变化量，∂n/∂T为温度-折射率关系系数，ΔT为温度变化，afc为折射率-载流子浓度关系系数，ΔNfc为载流子浓度变化。GaAs材料中∂n/∂T可取(3.7±0.5)×10-4K-1[26]，高功率半导体激光器的结温升一般大于25 K，其温升导致的折射率变化一般为10-2量级；afc为(1.2±0.2)×10-20cm3，而载流子浓度一般为1018量级，由此可知载流子注入所引起的折射率变化应为10-2数量级，故热透镜效应对侧向波导影响很大。折射率分布与空间坐标之间的关系如公式(6)所示：

(6)

其中，n(x)表示折射率随坐标分布函数；n0为材料原始折射率，对于GaAs一般取3.59[26]；α2为常数，大于零时表示正透镜。其焦距为：

(7)

其中l为自聚焦透镜厚度。慢轴发散角增量为：

(8)

其中，θ表示光束慢轴发散角的变化量，ω表示器件有源区的侧向宽度。

3 计算机模拟分析热透镜效应对激光器慢轴发散角的影响

为了深入研究热透镜效应对激光器输出光束慢轴发散角的影响，采用ANSYS软件对不同热功率条件下典型宽条形应变量子阱半导体激光器的工作状况进行了仿真模拟。仿真的主要依据是热传导方程，即当激光器处于稳态工作时，可用公式(9)来描述其热量与温度分布：

(9)

其中，K是器件某一构成材料的热传导系数，T表示器件某一部分的温度，Q表示器件的热功率密度。在激光器工作时，其所产生的热量一般源自于有源区载流子的非辐射复合、吸收和自发发射。因此本文在模拟热分析部分，将激光器中的热源全部视作来源于有源区，从而使计算一定程度上得以简化。

首先通过实验获得激光器的P-I-V特性，并测量其输出光的功率，则其热功率为总功率减去输出功率；将所得热功率加上器件引线焦耳热功率后进行模拟热分析。图2显示的是当器件的热功率达到10.3 W时，芯片前腔面温度的分布云图。

图2表明，激光器工作时的最高温度位于有源区，在慢轴方向温度沿有源区中心向两侧逐渐降低。

提取平行于结面方向温度分布数据拟合曲线(如图3所示)，可知有源区内慢轴方向的温度分布呈二次函数曲线，联立公式(5)～(8)能够获得等效热透镜的焦距、热致光束发散角与器件热功率的关系，如图4(b)所示。

表1 激光器各层材料参数

图2 激光器热功率为10.3 W时芯片内部温度分布

Fig.2 Internal temperature distribution of the chip when the laser thermal power is 10.3 W

图3 模拟所得激光器条行区沿慢轴方向的结温分布

Fig.3 Junction temperature distribution of the simulated laser strip row along the slow axis

图4(a)为仿真得到的不同热功率下器件中心最高温度，其随热功率的增加而升高，可看出两者之间呈现出线性关系。通过对数据拟合可知，当芯片的热功率每升高1 W时，其中心结温便会随之上升1.5 ℃，器件热阻为1.5 K/W。分析图4(b)可知，随着热功率的不断提升，芯片热透镜效应的焦距会随之减小，其输出光的慢轴发散角则会随之逐渐变大。当器件的热功率为10.3 W时，中心结温达到40.9 ℃，比注入条边缘温度高8.2 ℃，此时，热透镜焦距约为109.5 μm，慢轴发散角约为4.7°。半导体激光器在高功率工作时，结温随工作电流的增加愈加明显，有源区热功率密度比较高，热透镜效应对侧向波导有较大影响，导致慢轴发散角明显增大。

图4 模拟得到的最大结温(a)、激光器的热透镜焦距及慢轴发散角(b)随热功率增加的变化关系。

Fig.4 Relationship between maximum junction temperature(a), thermal lens focal length and slow axis divergence angle of the laser(b) as a function of thermal power increase.

4 实验结果及比较

为了系统地研究器件输出特性受温升影响的情况，选取了与计算机模拟建模相同结构的915 nm宽条型应变量子阱半导体激光器进行实验测试。实验用激光器芯片的电流注入宽度为0.18 mm，谐振腔的长度为4 mm。

实验搭建了如图5所示的温控平台：将LD芯片焊接在热沉上，然后安装在无氧铜制成的散热板上，通过TEC对散热板进行控温，该TEC由双向精密温控电源驱动，通过NTC热敏电阻传感器实时反馈散热板的温度，并采用PID程序来对TEC施加正反向电流；温度设置、PID参数、电流电压保护值等参数可在主机中进行显示和调整。通过对PID控温参数的优化，实验中将温度的控制精度稳定在了±0.01 ℃之内。激光器采用专用电源进行驱动，电流控制精度为0.1 A；利用Gentec-EO MAESTRO型光功率计测量激光的输出功率，使用一台HR4000CG-UV-NIR型光谱仪对激光的光谱分布进行测量。测量激光器输出光束的慢轴发散角时，采用了一台CCD相机，通过对激光远场光斑进行采集、计算机对数据进行处理，最终获得了光束的光强分布情况。

图5 实验系统。(a)双向温控主机；(b)温控平台。

Fig.5 Experimental system. (a)Bi-directional temperature control host. (b)Temperature control platform.

首先，通过温控平台将激光器的工作温度控制在测试温度下，获取了输出光谱线随温度变化的情况以及器件的波长温漂系数，如图6所示。

从图中可以看出，随着激光器的温升加剧，其输出光的光谱出现了明显红移，这与2.2.3中的理论描述一致。

根据25，50，70 ℃温度条件下器件在热功率7 W工作的波长漂移(从915 nm漂移到931 nm)，可得器件的波长温度系数约为0.4 nm/℃；室温下，通过对器件在不同热功率下的激光光谱进行测量，能够计算出激光器的输出光波长随热功率的变化系数约为0.6 nm/W。

图6 激光光谱随温度升高的变化特性

然后，我们测量了不同温度下激光器的P-I与V-I特性，并降低平台的温度使输出波长稳定在915 nm，得到了恒定结温条件下的P-I-V参数，如图7、图8所示。

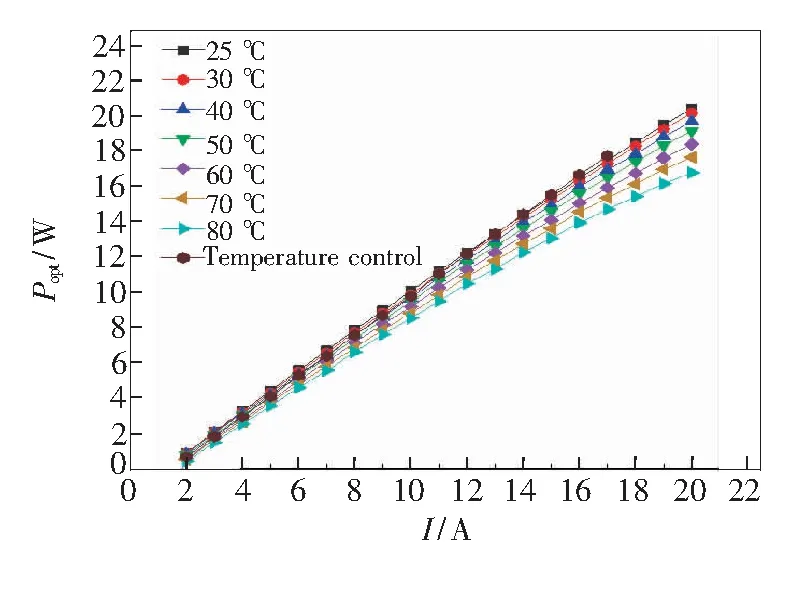
图7 激光器P-I随温度升高的变化特性

Fig.7 Variation characteristics of laserP-Iwith increasing temperature

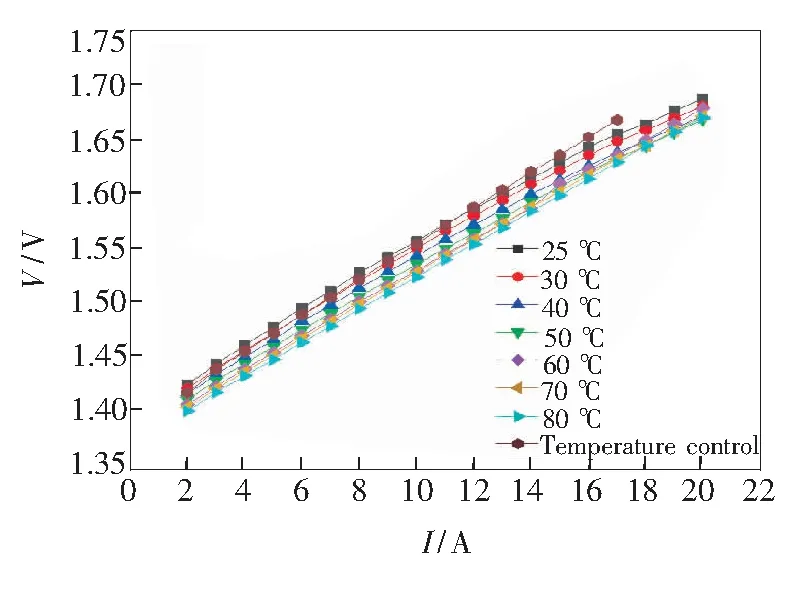
图8 V-I随温度升高的变化特性

图7给出了在不同温度下，器件输出功率随注入电流变化的情况。图中标注为Temperature control的曲线，表示的是波长恒定在915 nm时所测量的输出激光功率随注入电流变化的情况。通过分析可知：当器件的工作结温恒定时，由于对注入载流子的良好限制特性，得到随工作电流增大输出光功率随之呈近似线性增大的实验结果；而对于一定的注入电流，激光器输出光功率则与工作温度呈负相关关系。

测量表明，激光器的斜率效率从25 ℃的1.1 W/A降低到了80 ℃的0.9 W/A，且当激光芯片的结温(峰值波长)恒定时，其斜率效率可稳定在较高的水平。当激光器工作温度较低时，输出光功率与电流呈较好的线性关系；而当温度高于50 ℃时，两者之间的线性度出现了下降，这是由于激光器结温升高导致漏电流增加、发光效率降低，从而引起器件的光电转换效率下降、P-I曲线的线性度变差。

图8为不同测试温度下工作电压随电流的变化关系，图中标注为Temperature control的曲线，表示的是波长恒定在915 nm时所测量的器件电压随注入电流变化的情况。由此计算出不同温度下的串联微分电阻，当温度从25 ℃升高至80 ℃时，串联电阻从16.3 mΩ下降到15.5 mΩ。温度对串联电阻的影响不大。

通过对P-I曲线数据进行拟合，得到激光器不同温度下的阈值电流，如图9所示。

图9 阈值电流随温度升高的变化特性

从图中可以看出，阈值电流随温度的升高而增大，这与2.2.1所述理论相符。当温度从25 ℃升高到80 ℃时，阈值电流从1.0 A升高到1.3 A，用公式(2)可计算出其特征温度，为89.4 K。由此可以进一步计算出器件的热阻，为1.5 K/W，这一数值与计算机模拟运行所得到的数值是一致的。

我们使用CCD相机测量了温度在25 ℃下，工作电流分别为5，10，15 A时，激光器输出光束的远场光斑，并采用计算机对数据进行了处理，所得图像如图10所示。

图10 工作电流分别为5，10，15 A时实测的远场光斑。

Fig.10 Measured far-field spot when working current is 5, 10, 15 A.

从图10中可见，远场光斑由多个光丝组成，各光丝的位置和强度随电流变化，数量随电流增加而增多，光束发散角逐渐变大，这在一定程度上印证了热透镜效应以及载流子分布等对激光器侧向波导的影响。

通过对10 A时激光远场数据进行处理，得到了三维的光斑分布情况，如图11所示。

从图11可见，远场光斑近似为椭圆状，其在快轴方向的强度分布为形成单模高斯分布，而在慢轴方向的强度分布则表现为多模多峰的形态。

我们将计算机仿真模拟所得到的结温随热功率变化的数据绘制成曲线，并与实验测量结果放在一起比较，如图12所示。

由图12可以看出，模拟仿真与实际测量的曲线趋于一致，说明模拟数据具有较高的可信性。

图13展示了实验测得的以及仿真模拟出的激光器输出光束慢轴发散角随电流变化的情况。

可以看出，对于实验测得的曲线，当注入电流达到6 A时曲线出现了局部的下降，在较小电流下，由于较少的横模达到激射状态，其模式竞争随电流增加的随机性可能导致更少的低阶横模得到增强，从而引起光束发散角偶然性减小。当工作电流小于8 A时，实验测量的发散角大于仿真模拟的数值；而当工作电流大于8 A时，实验测量值则小于模拟计算的数值。图像中的两个曲线虽然都呈现出慢轴发散角随电流的增加而增大的趋势，但在具体变化关系中又表现出了一定差异，说明模拟计算的数值还是更趋向于理想化。

图11 工作电流为10 A时远场光斑三维强度分布

Fig.11 3D intensity distribution of far-field spot when the operating current is 10 A

图12 模拟仿真和实验测得的结温随热功率变化曲线

Fig.12 Curves of simulation and experimentally measured changes in junction temperature with thermal power

图13 实测以及模拟的激光器慢轴发散角随电流变化情况

Fig.13 Measured and simulated laser slow axis divergence angle changes with current

5 结 论

本文实验测量了一种915 nm宽条形应变量子阱半导体激光器在不同环境温度、不同工作电流下的输出功率，分析得到了对应温度下的阈值电流。结果表明，当芯片温度升高时，其阈值电流明显增大，输出光功率显著降低，光谱线出现红移，温度每升高1 ℃，波长增加0.4 nm。计算得到器件的热阻为1.5 K/W。

研究了激光器在不同热功率下的热透镜焦距及其对慢轴发散角的影响，仿真计算和实验测量得出的结果基本一致：当热功率增大时，热透镜等效焦距趋于减小，输出光慢轴发散角明显增大。因此，在设计高功率半导体激光器时，可以适当增加条宽，并采用散热良好的封装结构，以最大程度减小热透镜效应对慢轴发散角的影响。

实验测量了恒定结温(峰值波长)条件下激光器的输出光功率特性，发现其斜率效率得到了显著提升，反映出结温升所引起的注入载流子泄漏得到了有效抑制，可有效改善激光器的功率输出特性。