基于动态规划的非均匀杂波环境中的复似然比检测前跟踪算法
安政帅
(中国电子科技集团公司第二十研究所 西安 710068)
0 引言
杂波主要来自起伏的地面,树林,高大的建筑物和气象云雨的后向散射。随着目标所处环境的复杂化,雷达检测目标时不可避免地会受到非均匀杂波的干扰[1],尤其是当目标很微弱时,非均匀杂波的存在使雷达对微弱目标的检测能力明显下降。先验信息的应用是提高雷达目标检测与跟踪性能的重要途径之一,也是贝叶斯统计理论的核心问题。杂波的非均匀性[2]是影响雷达目标探测的重要因素[3]之一,将杂波统计特性的先验信息应用于目标检测与跟踪算法的设计,将有利于提高非均匀杂波中目标的检测与跟踪性能[4]。
近年来,随着目标多样化的发展,目标信号越来越弱,特别是对于非均匀强杂波环境中的微弱目标的检测越来越困难。为了解决低信噪比下目标的检测难题,出现了先跟踪后检测(Track Before Detect,TBD)方法。与传统的先检测后跟踪的不同之处在于,TBD在单帧数据不设门限或设非常低的门限,然后将雷达回波数据存储起来,在多帧联合处理后宣布检测结果并同时估计出目标航迹。该算法检测微弱目标的高效性与鲁棒性已经得到了证实[5]。早期关于检测前跟踪的研究主要集中在光学图像处理中弱小目标的检测,例如,三维匹配滤波算法[6]和递归动目标显示算法[7],但是这两种算法需要知道目标速度的先验信息,否则会出现性能损失。然而动态规划(Dynamic Programming, DP)方法[8-12]并不需要知道目标速度的先验信息,可以跟踪弱机动目标,并且计算量小,易于实现。
在雷达中,一般假设背景噪声服从复高斯分布,这意味着当目标存在时,分辨单元的回波强度服从莱斯分布,而当目标不存在时,分辨单元的回波强度服从瑞利分布。假设空间噪声不相关,每帧数据的概率可以表示为单个分辨单元概率的乘积,这里可以将这个概率表示为似然比的形式。但是莱斯分布和瑞利分布仅仅为数据幅度的函数,因此这种方法并没有利用相位信息。文献[13]提出了一种复似然比方法,利用了数据的相位信息,并用粒子滤波方法验证了该方法的有效性。但是在基于动态规划检测前跟踪算法的研究中,目前的文献是在包络检波以后利用数据的幅度信息进行的,这导致了信息损失。
雷达信号处理的目标之一是解决目标与环境间的矛盾,而对目标检测影响最严重的环境干扰就是杂波[1]。对于雷达监视的某一特定区域,可以按照一定的方法建立雷达威力范围内杂波强度的分布图——杂波图。当雷达对该区域照射时,可以充分利用建立的杂波图信息,从而提高对该区域微弱目标的检测与跟踪能力[14-18]。已有文献[8-12]在基于动态规划的检测前跟踪算法的研究中大多只简单地考虑了均匀的高斯背景,没有考虑复杂的非均匀杂波背景下的目标检测与跟踪问题。
基于以上问题和研究,本文提出了基于动态规划的非均匀杂波环境下的复似然比检测前跟踪方法。针对非均匀杂波背景下的微弱目标检测问题,提出了将先验的杂波图信息引入动态规划值函数中,进而给出了适合于非均匀杂波环境下的DP-TBD算法。仿真结果表明杂波图先验信息的使用提高了算法的检测与跟踪性能;本文将复似然比函数作为动态规划的值函数,不仅利用了相位信息,而且降低了运算量,仿真验证了该算法的有效性。
1 系统模型
1.1 目标模型
为了简化,假定一个目标靠近雷达且做匀速直线运动。令K表示动态规划处理的帧数,在第k次扫描时目标的状态为xk=(xpk,vk,Ik),xpk表示目标的位置,vk表示目标的速度,Ik为目标回波强度,则目标的状态方程为
xk=Fxk-1+vk-1
(1)
其中vk-1表示k-1时刻的过程噪声,用于衡量目标状态的不确定性,F为转移矩阵

(2)
其中T为相邻两帧数据的时间间隔。
1.2 量测模型
假设观测方向共N个分辨单元,每个分辨单元的大小为Δ×Δ,一次动态规划处理的帧数为K,则观测方程[13]为
zk=exp(jφ)h(xk)+nk
(3)
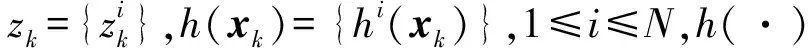
目标的航迹定义为第一帧到第K帧的一系列连续的目标状态{x1,x2,…,xK}。
动态规划要解决的问题就是:希望从第一帧到第K帧的所有量测中确定最可能的目标航迹,且

(4)
其中VDT为根据给定的虚警率设定的检测门限。
2 似然比函数的建立
2.1 复高斯背景下的似然比函数
通常情况下,假定测量噪声是不相关的,因此噪声协方差矩阵R可以表示为σ2I,这里I表示单位矩阵。 现存的文献大多只考虑分辨单元信号的幅度信息。这里将只利用幅度信息构造的似然比函数称为幅度似然比函数。下面给出现存文献中复高斯背景下幅度似然比函数的结果,具体推导可以参阅文献[13]。
整幅图像的幅度似然比函数为
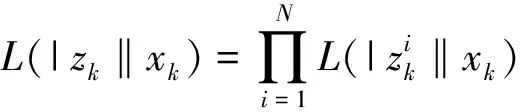
(5)
其中上标“H”表示共轭转置,I0(·)为零阶贝塞尔函数。
式(5)定义的这种幅度似然比函数没有利用数据的相位信息,因此它造成了一定的信息损失,而且幅度似然比函数需要对每一个分辨单元计算多次贝塞尔函数。实践经验表明,当利用该幅度似然比函数作为动态规划算法的值函数时,贝塞尔函数的计算是该算法中最耗费计算资源的部分。在式(5)的基础上,文献[13]提出了一种新的似然比函数,这里将这种似然比函数称为复似然比函数,下面给出该似然比函数的结果,详细推导可以参阅文献[16]。
复似然比函数为

(6)
其中R为噪声协方差矩阵。
2.2 基于杂波图先验信息的似然比函数
雷达监视的某一特定区域的地表信息在一定时间是相对稳定的。将杂波模型与雷达监视的该区域的雷达回波数据结合起来,可以计算出每一个分辨单元内的杂波强度,因此,很容易建立雷达监视的某一特定区域的杂波强度的分布图——杂波图[1]。在本文,假定某一特定监视区域的杂波图是已知的,并且杂波图提供了每个分辨单元内的杂波强度信息。
假定雷达监视的某区域的杂波强度可以表示为
(7)
对于高分辨率雷达的目标检测与跟踪,非均匀杂波是影响雷达目标检测性能的重要因素之一。非均匀杂波往往会引发大量的虚警点,从而掩盖真正的目标信息,进而导致雷达监视区域内观测数据可信度的降低。因此,在进行动态规划积累时,真正的目标状态很难在有效搜索范围内找到,这使得值函数得不到正确的积累,导致最终恢复的航迹包含了大量的虚假航迹,从而增加了后续处理伪航迹的计算量。非均匀杂波使得检测跟踪复杂环境下的微弱目标变得十分困难,充分利用杂波统计特性的先验信息将有助于提高非均匀杂波中目标的检测与跟踪性能。根据雷达观测区域内的杂波图先验信息,在上节复高斯背景下似然比函数的基础上,本文在构造似然比函数中加入先验的杂波图信息,从而提高对非均匀杂波中微弱目标的检测与跟踪性能。
假定雷达监视区域内每个分辨单元内的杂波不相关,则杂波相关矩阵可以表示为
(8)
下面将杂波图的先验信息加入到似然比函数中,具体实现如下:
1)当只考虑雷达回波信号的幅度信息时,包含先验杂波图信息的幅度似然比函数为
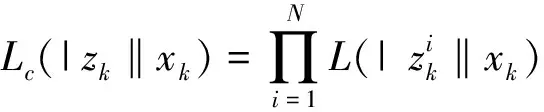
(9)
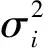
2)当同时考虑雷达回波信号的幅度和相位信息时,包含先验杂波图信息的复似然比函数为
I0(|h(xk)HR-1zk|)
(10)
其中R为杂波的相关矩阵。
上文改进的似然比函数充分利用了杂波图中杂波的强度和位置信息,当利用式(9)或式(10)作为动态规划的值函数进行检测前跟踪,在动态规划积累过程中,该算法会大大减小与强杂波点关联的概率,从而降低后续航迹处理的计算量。
总之,与式(9)相比,式(10)不仅包含了复数据的相位信息,提高了数据的利用率,而且,大大减小了贝塞尔函数的计算,提高了系统的实时性。与此同时,式(10)也扩展了非均匀杂波背景下似然比函数的适用范围,因为现实中雷达监视的某一区域不同分辨单元之间的杂波往往是相关的。因此,利用式(10)作为动态规划的值函数不仅可以提高系统的实时性,而且能更有效的检测跟踪非均匀杂波环境下的微弱目标。
3 基于动态规划的检测前跟踪算法
3.1 算法流程
将动态规划应用到TBD技术中,现存的文献中在构造动态规划的值函数时只应用了数据的幅度信息,并且现存的算法大都是针对高斯噪声背景中的目标检测,并不适用于非均匀杂波环境。为了将动态规划算法更好的应用于工程实践,下面将第2节提出的式(10)作为动态规划的值函数,对非均匀杂波环境下的微弱目标进行检测前跟踪。基于杂波图信息的复似然比动态规划算法具体实施如下:
1) 初始化:对于k=1所有的状态x1
I(x1)=Lc(z1|x1)
(11)
Ψx1(1)=0
(12)
其中I(·)为值函数,Ψ(·)为回溯函数,Lc(·)为本文改进后的包含杂波图信息的似然比函数。
2) 递归积累:2≤k≤K对所有的状态xk
(13)
(14)
其中Z1:K={z1,z2,…,zK},τ(xk)为前一帧能转移到状态xk的所有状态xk-1组成的集合。
3) 迭代终止:找出值函数超过门限VDT的状态序列
(15)
其中VDT为根据给定的虚警率设定的检测门限。
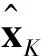
(16)
3.2 航迹处理
动态规划算法虽然使目标能量沿航迹得到了有效积累,然而能量在沿目标航迹积累的每一个阶段,目标能量都会发生扩散,且积累帧数越多,能量扩散越严重。这使得该算法很难设置合适的检测门限,进而导致恢复的目标航迹中含有大量的虚假航迹。另一方面,一些强杂波点也会产生一些虚假航迹。因此,必须想办法去除这些虚假的目标航迹。
目标的能量扩散和强杂波点都会引起虚假目标航迹的产生,但是它们产生的虚假航迹的特征是不同的。目标能量扩散引起的虚假航迹的一个明显特征是这些虚假航迹与真实的目标航迹存在部分航迹的重合[11]。而杂波引起的虚假目标航迹是随机的,因此航迹的长度往往远远短于目标的航迹[20]。其于以上分析,航迹处理的具体步骤如下:
1) 航迹回溯,得到候选目标航迹集合A,并初始化i=1。
2) 构造目标航迹组:找到最大值函数恢复的目标航迹(原始航迹)存入集合Bi,并将与该航迹共享M个状态以上的航迹也存入集合Bi。然后从候选目标航迹集合A中将集合Bi中的航迹删除。这里的M与积累的帧数K和检测门限VT有关。
3) 消除子航迹:将集合Bi中与原始航迹共享小于N个状态的航迹删除,这里M≤N≤K。如果N=K,则集合Bi中的航迹便为估计的初级目标航迹并存入集合C中,否则对集合Bi中航迹求取平均值存入集合C作为初级目标航迹。这里的N与信杂比有关,当信杂比很大时,取N=K;信杂比越小,N取值越接近M。
4) 递归:如果候选目标集合A不为空,则令i=i+1,重复步骤2)和3)。
5) 对集合C中的每一条初级目标航迹求取长度。如果航迹长度大于阈值L,则该航迹作为估计的目标航迹并输出。这里的L与目标运动速度和积累帧数有关。
4 仿真分析
虚警概率Pfa定义为最大杂波状态值函数超过检测门限VT的概率[21]。
(17)
这里xK∈{杂波状态}。
检测概率Pd:至少存在一个状态与目标的真实位置误差在两个分辨单元内,速度单元与真实的速度单元相同,并且使最终状态的值函数超过检测门限的概率[21]。
(18)
这里xK∈{与K时刻目标所在位置相距小于两个距离单元且速度等于真实速度的所有状态}。
检测跟踪概率Pt:被检测的目标航迹在每一帧的位置,与相应的真实目标航迹在每一帧的真实位置的差距在两个距离单元内的概率[21]。
为了比较本文提出的算法与传统方法的性能,仿真参数设置如下:
设一个目标靠近雷达且做匀速直线运动,距离分辨单元50个,目标的最大速度为2个分辨单元/帧,积累15帧,虚警率为Pfa=10-3,仿真的蒙特卡罗实验均进行500次。
4.1 非均匀杂波环境下复似然比算法结果与分析
从图1可以看出DP算法恢复的目标航迹中包含大量的虚假目标航迹,这是由于动态规划的每一个阶段目标能量沿航迹进行积累的同时发生了能量扩散,而且积累的帧数越多,能量扩散得越严重,产生的虚假目标航迹越多。图2为利用本文提出的航迹处理算法对图1进行伪航迹去除后的结果,从该图可以看出本文提出的算法能够比较准确的恢复非均匀杂波环境下微弱目标的航迹。

图1 DP恢复的目标航迹与真实航迹
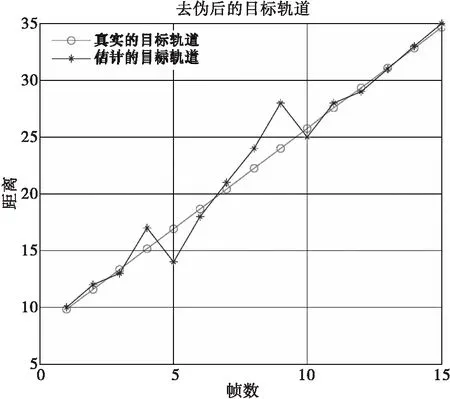
图2 去除伪航迹后估计的目标航迹与真实航迹
4.2 非均匀杂波环境下幅度似然比与复似然比对比实验与分析
4.2.1 复杂度对比实验与分析
表1 两种方法运行时间对比表

算法平均一次的运行时间/s幅度似然比3.6复似然比1.4
从表1可以看出利用幅度似然比函数作为动态规划的值函数和利用复似然比函数作为动态规划的值函数在相同的仿真场景下的运行时间,前者是后者的两倍还多。这是因为每一个分辨单元,每计算一次似然比函数,幅度似然比函数需要计算N次贝塞尔函数(现实中N往往很大),而复似然比函数只需要计算一次贝塞尔函数,并且到目前为止,贝塞尔函数的计算是利用这种似然比函数最耗费计算资源的部分。从该仿真实验可以看出本文提出的新方法在运算效率比以前的方法有了很大的提高。
4.2.2 检测与跟踪性能实验对比与分析
图3为利用幅度似然比函数作为动态规划的值函数和利用复似然比函数作为动态规划的值函数在虚警率相同的情况下不同信杂噪比下的检测概率曲线。从图3可以看出在相同的仿真条件下,本文提出的方法比以前的方法检测概率有了大约0.5 dB的提高。图4为利用幅度似然比函数作为动态规划的值函数和利用复似然比函数作为动态规划的值函数在虚警率相同的情况下不同信杂噪比下的检测跟踪概率曲线。从图4可以看出在相同的仿真条件下,本文提出的方法比以前的方法检测跟踪概率有了一定的提高。
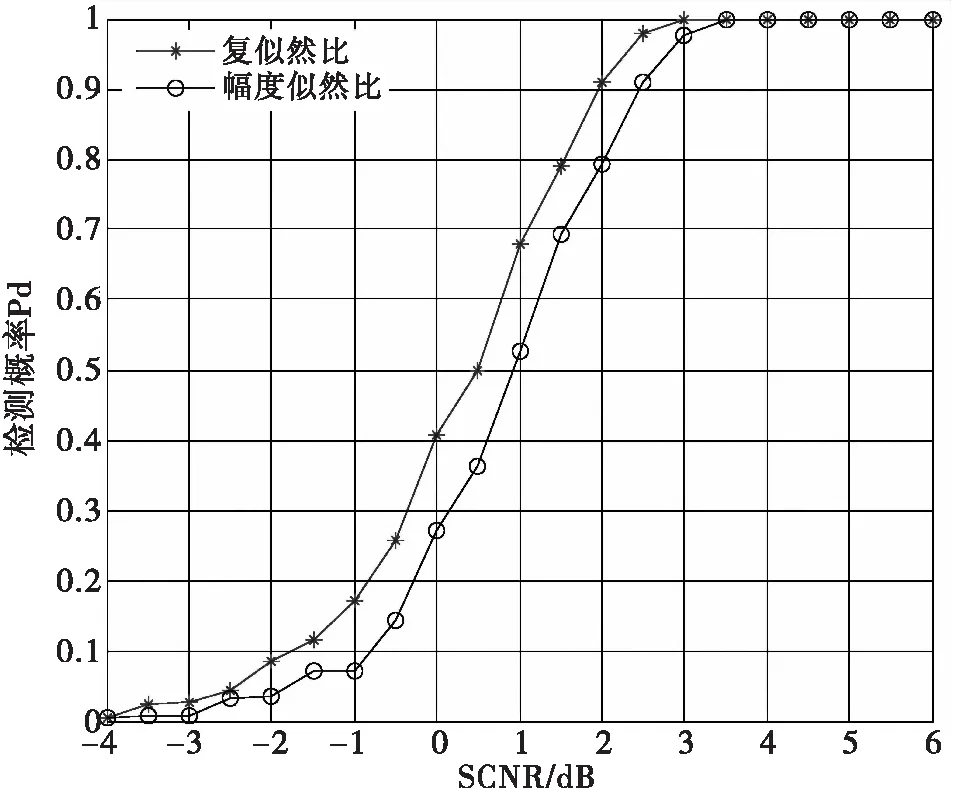
图3 复似然比与幅度似然比检测概率对比

图4 复似然比与幅度似然比跟踪概率对比
通过对这两种方法检测概率和检测跟踪概率的比较,可以看出本文提出的方法无论是在检测性能还是在跟踪性能上都优于现存的只利用数据幅度信息的方法,从而证明了该方法的有效性。当目标占据的分辨单元越多时,可以利用的信号信息越多,本文提出的复似然比方法的优势越明显。
4.3 非均匀杂波环境下利用杂波图信息与不利用杂波图信息复似然比算法结果与分析
图5为利用杂波图信息与不利用杂波图信息在杂波能量服从均值为2.4,方差为7.2的伽玛分布下的检测概率曲线,从该图可以十分明显地看出,利用杂波图信息可以大大提高目标的检测概率。图6为利用杂波图信息与不利用杂波图信息在杂波能量服从均值为2.4,方差为7.2的伽玛分布下的检测跟踪概率曲线,从图中可以看出利用杂波图信息可以一定程度上提高目标的跟踪概率。
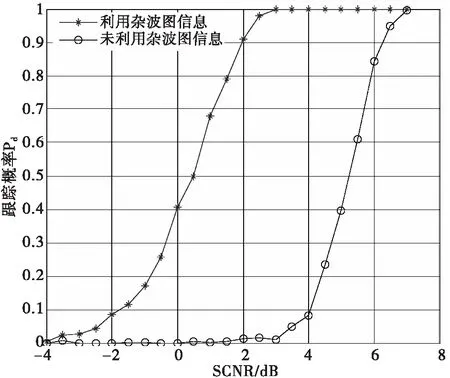
图5 利用与不利用杂波图信息检测概率对比

图6 利用与不利用杂波图信息跟踪概率对比
综合图5和图6,可以得出这样的结论:在非均匀杂波环境下,充分利用已经建立的杂波图信息,可以更有效地检测跟踪复杂环境下的微弱目标。
5 结束语
本文提出了一种基于动态规划的非均匀杂波环境下的复似然比检测前跟踪算法,目的是充分利用先验的杂波图信息,从而克服以前算法中检测非均匀杂波环境中微弱目标性能差的缺点。并且该算法在构造似然比函数时利用了数据的相位信息,不仅提高了检测与跟踪性能,而且减小了计算量。与此同时,在航迹处理步骤中改进了选取目标航迹的方法,这样可以使估计的航迹更加准确。仿真表明,杂波图先验信息的利用充分提高了该算法检测非均匀杂波中微弱目标的性能,并且与幅度似然相比,复似然比性能好,而且计算量小。杂波图信息的利用虽然提高了非均匀杂波环境中检测与跟踪微弱目标的能力,但是如何将该算法更好地应用到工程实践中尚需进一步研究。

