细胞膜机制萤火虫算法优化多阈值Otsu图像分割
刘鑫晶,刘彦隆,徐鑫鑫
(太原理工大学 信息与计算机学院,山西 晋中 030600)
1 引 言
数字图像处理是一种将图像转换为数字形式并对其执行某些操作的方法.其中,图像分割这一步骤是非常重要的,其精确性对整个图像处理得到的结果有着至关重要的影响.基于阈值的分割算法具有分割稳定性强,模型简单及鲁棒性强的优点而得到了研究者们十分广泛地研究和应用.最大类间方差法(Otsu)是由日本学者Nobuyuki Otsu在1979年提出的具有代表性的阈值确定方法[1],Otsu算法的基本原理是最小二乘法.为了使该算法能够适应具有多个目标的复杂图像,有研究者将Otsu算法从单阈值扩展到多阈值[2].多阈值Otsu算法解决了复杂图像的分割问题,但随阈值个数逐渐增多,算法运算时间会指数增长,这也是所谓的NP(nonlinear problems)难题[3].
近几年,为了减少多阈值Otsu算法的运算时间,如布谷鸟搜索(CS),人工蜂群(ABC),萤火虫算法(GSO),粒子群优化(PSO),差分进化(DE)等启发式算法用于图像分割[4-8].GSO算法不但可以找到局部最优解,还能够得到全局最优解,则在多阈值Otsu图像分割中有普遍应用.Assistant等人[9]提出了基于GSO算法优化的最大期望算法应用于多阈值分割,Simone A.Ludwig等人[3]提出了一种适用于多阈值图像分割任务的改进的GSO算法(EGSO).国内,于超杰等人[10]提出了基于反向学习策略的改进型萤火虫算法(OBLFA)应用于Otsu图像分割,申玄京等人[11]提出了基于GSO算法的递归多阈值Otsu算法,陈凯等人[12]提出了基于反向GSO算法针对缺陷图像的多阈值分割.
标准GSO算法寻求最优解的过程中其精度低,速度慢和容易陷入局部最优值,即“早熟”现象[13].虽然国内外针对标准GSO算法存在的这些缺点提出了许多改进型算法,并研究应用于多阈值图像分割中,但是结果都不尽理想.
为了更好地解决标准GSO算法存在的收敛速度慢和易出现“早熟”现象等问题以及多阈值图像分割的时间复杂度高的NP难题,本文提出了一种基于细胞膜和GSO混合优化算法的多阈值Otsu图像分割.细胞膜优化算法采用了保留最优解策略,将其应用于GSO算法中,收敛速度提高并能够有效避免GSO算法陷入局部的最优值.采用混合优化算法将对阈值的搜索问题转换成对目标函数求它的最优解问题,很好地降低了其时间复杂度.
2 萤火虫混合优化算法的产生
2.1 标准的萤火虫算法
标准的GSO算法[14]主要包括5个步骤:初始化GSO中参数,更新荧光素值,选择移动的方向,移动到更新的位置,更新决策域的半径大小.
1)初始化GSO中参数
将M只萤火虫随机地分在一个D维的目标空间内,每只的初始荧光素大小l0和感知半径r0一样.并初始化GSO算法的最大迭代次数Tmax.
2)更新荧光素值
所有萤火虫在下一次迭代前,都依据式(1)得到新的荧光素浓度.
li(t+1)=(1-ρ)li(t)+γJ[xi(t+1)]
(1)
3)选择移动的方向
在每次迭代时,每只萤火虫i都会在决策域半径内寻找满足以下两个前提的同伴j的集合Ni(t):一是萤火虫j在i的决策域范围中;二是萤火虫j的荧光素浓度值必须大于i.然后,萤火虫i在集合Ni(t)中使用轮盘赌法选择一只萤火虫.Ni(t)内每只萤火虫被选的概率如式(2)所示.
(2)
4)移动到更新的位置
萤火虫i向第3)步选好的萤火虫j进行第t+1次位置更新,如式(3)所示.
(3)
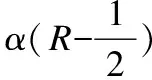
5)更新决策域半径
每次迭代完后,决策域半径进行更新,如式(4)所示.
(4)
2.2 自适应步长的萤火虫算法
2018年李顺等[15]提出一种自适应步长GSO算法(adaptive-step GSO,A-GSO).A-GSO中引入荧光因子Hi,使得在搜索时动态改变萤火虫的移动步长,使算法在一定程度上改善了“早熟”现象,提高求解速度.
荧光因子Hi的大小由式(5)计算.
(5)
式中,Xi,Xm分别表示萤火虫i和当代荧光素浓度最大的萤火虫所在的位置;dmax表示当代最优的萤火虫到其余萤火虫距离的最大值.
移动步长s按照式(6)进行调整.
si=smin+(smax-smin)×Hi
(6)
2.3 基于细胞膜和萤火虫混合优化算法
虽然A-GSO在一定程度上改善了标准GSO的“早熟”问题,但是该算法在运行时很容易出现一些萤火虫的同伴集合Ni(t)为空集,这些萤火虫在迭代过程中将不会移动到更新的位置,导致算法的收敛速率降低并且容易陷入局部最优.2011年林土胜、谭世恒等人[16]提出了一种新型的全局优化算法,即细胞膜算法(CM),并且通过数值实验,已经验证该算法有很好的全局寻优能力和快速收敛能力.但是该算法目前没有得到广泛的应用.本文借鉴该算法中在迭代前将物质分类和保留最优解的思想将CM算法运用在A-GSO算法上,将两个算法进行结合,得到细胞膜和萤火虫混合优化算法(CMA-GSO).结合了细胞膜算法思想和自适应步长思想的萤火虫算法很好地改善了标准GSO算法的“早熟”问题,收敛速度慢以及求解精度不高的问题.CMA-GSO算法流程图如图1所示.
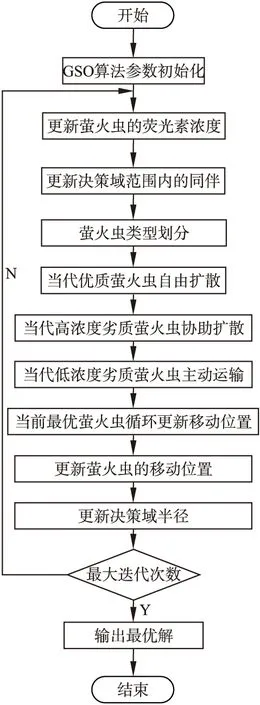
图1 CMA-GSO算法流程图Fig.1 Flow chart of CMA-GSO algorithm
CMA-GSO算法是对标准的GSO算法的“使用轮盘赌注法选择移动方向”这一步骤使用了细胞膜算法中对物质类型进行划分以及每种物质有各自不一样的运动方式来代替了.CMA-GSO算法的详细步骤如下所示:
1)萤火虫类型划分
首先把所有的萤火虫的荧光素浓度从小到大排序,排在前P比例的萤火虫划分为当代优质萤火虫,排在后面的萤火虫划分为当代劣质萤火虫.然后对劣质萤火虫再划分成两类:高浓度和低浓度.对于萤火虫i,它所处的浓度定义为其决策域内同伴萤火虫数量占总萤火虫数的百分比,如式(7).
(7)
式中,n表示萤火虫i决策域内同伴萤火虫数量;m表示目标空间总萤火虫数量.所有浓度的平均值为MeanCon,如式(8).
(8)
若某劣质萤火虫所处的浓度大于MeanCon,那么该萤火虫划分为高浓度劣质萤火虫,否则划分为低浓度劣质萤火虫.
2)当代优质萤火虫自由扩散
优质萤火虫即代表细胞膜算法中的脂溶性物质.自由扩散是指脂溶性物质由膜的高浓度侧向低浓度侧的扩散过程,整个过程不需要载体和能量.对于每一个高浓度优质萤火虫sXi将向低浓度萤火虫群LX方向扩散locn次,选取最好的扩散位置处的萤火虫作为最终的结果.其详细计算方法如式(9)所示.
(9)
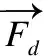
经过此过程后,由原来的优质萤火虫群sX转变为新的优质萤火虫群newsX.
3)当代高浓度劣质萤火虫协助扩散
高浓度劣质萤火虫即代表细胞膜算法中的高浓度非脂溶性物质,在细胞膜中,高浓度非脂溶物质做协助扩散由细胞膜的高浓度侧转移到低浓度侧.此过程只需要载体,不需要能量,因此引入载体因子cf.高浓度劣质萤火虫hiXi的载体因子cfi如式(10)所示计算.
(10)
高浓度劣质萤火虫存在两种运动方式.当存在载体时,萤火虫进行协助扩散,向低浓度方向运动,同上面自由扩散的计算方法类似.当不存在载体时,其向当前最优萤火虫Xbest方向扩散locn次,并选取最好的扩散位置处的萤火虫作为最终的结果.其扩散方法如式(11)所示.
(11)
经过此过程后,由原来的高浓度劣质萤火虫群hiX转变为新的高浓度劣质萤火虫群newhiX.
4)当代低浓度劣质萤火虫主动运输
低浓度劣质萤火虫即代表细胞膜算法中的低浓度非脂溶性物质.在细胞膜中,低浓度物质主动运输,从细胞膜的低浓度侧转移到高浓度侧,须要载体和能量.需要引入载体因子cf和能量因子ef.载体因子cfi的计算方法与上一步类似.能量因子efi的计算方法为:按照低浓度劣质萤火虫的荧光素值从小到大进行排序,荧光素值最大的萤火虫其能量因子为efmin,荧光素值最小的萤火虫其能量因子为efmax,其它萤火虫的能量因子ef介于efmin和efmax之间,并按照排序的顺序线性计算.其中,efmin和efmax为[0,1]内的常数,在这里取efmin和efmax分别为0和1.
对于某低浓度劣质萤火虫liXi存在三种可能的运动方式,首先判断是否满足能量条件,其次判断是否满足载体条件.因此低浓度劣质萤火虫liXi的三种可能的运动方式分别为:一是能量条件和载体条件同时满足时,萤火虫liXi进行主动运输,向高浓度萤火虫群HX方向运动locn次,详细运动公式与优质萤火虫自由扩散的方法类似,这里不再赘述;二是满足能量条件而不满足载体条件时,萤火虫liXi向当前最优萤火虫Xbest方向扩散locn次;三是不满足能量条件时,萤火虫liXi在其决策域半径内随机运动locn次,运动方式如式(12)所示.最后需要选取最好的扩散位置的萤火虫作为最终的结果.
newliXi=ld+rand()×(ud-ld)
(12)
经过此过程后,由原来的低浓度劣质萤火虫群liX转变为新的低浓度劣质萤火虫群newliX.
5)当前最优萤火虫循环更新移动位置
在优质萤火虫附近往往会存在更优萤火虫,充分发掘当前最优萤火虫决策域空间,有利于提高寻优精度.以当前最优萤火虫Xbest为中心进行搜索,向更亮的萤火虫运动,不断地缩小决策域半径,进行反复运动.最后得到新的最优萤火虫newXbest即为当前全局最优萤火虫.
3 混合优化算法应用于多阈值Otsu图像分割
3.1 多阈值Otsu图像分割
Otsu指出最大类间原则和最小类内原则基本等价,本文采用最大类间原则.
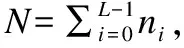
设图像中设有n个待区分的类,有n-1个阈值T1,T2,…,Tn-1将图像分为n个类.这些类分别表示为:
C0={0,1,…,T1},…,Cm={Tm+1,…,Tm+1},…,Cn-1
={Tn-1+1,…,L-1}
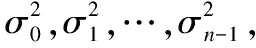
(13)
(14)
(15)
式中,k=0,1,…,n-1,T0=0,Tn=L.
整幅类间方差为:
(16)
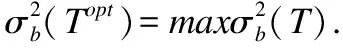
3.2 混合优化的多阈值Otsu图像分割算法
多阈值Otsu计算过程的伪代码如下所示:
Fori0 toL
Forji+1 toL
Forkj+1 toL
⋮
begin
maxVal=max(maxVal,cal(4))
t=canSwap(i,j,k,…)
end
可见,如果将一幅图像使用n-1个阈值分割,则这个算法的解空间是n-1维的.在解空间中任意一个n-1维向量都需要计算式(16)和式(14),算法的时间复杂度为O(Ln).
因此,本文考虑在对多阈值Otsu图像分割的阈值搜索过程中使用CMA-GSO优化算法将对最佳阈值的寻找过程转变为对目标函数的寻优问题,将多阈值Otsu图像分割的最大类间方差准则下的函数式(16)作为目标函数带入到CMA-GSO优化算法中,得到最优阈值.从而降低算法的时间复杂度.
4 实验结果与分析
为了验证本文提出的基于CMA-GSO优化的多阈值Otsu图像分割算法在复杂多目标图像分割上的分割效果和在算法运行速率上的优越性,本文选取Boats图、Camera图、MRI图和Saturn图四幅图像作为测试对象分别进行双阈值、三阈值、四阈值、五阈值图像分割.并将本文提出的方法与经典多阈值Otsu法、GSO优化多阈值Otsu法进行对比.MRI图是脑部核磁共振图[17],对MRI图进行多阈值分割有助于对脑部病情的诊断,具有现实意义.实验在2.80GHz CPU和8.00GB内存的PC机、window10.0操作系统和Matlab R2015b环境中进行的.
实验中对CMA-GSO优化算法的参数设置如下:最大迭代次数Tmax=200;萤火虫个数M=100;初始荧光素l0=5;初始感知半径r0=10;划分比例P=50%;空间维数D=10;挥发因子ρ=0.4;介质吸收系数γ=0.6;扩散次数locn=10.图2给出了4幅图像的原始灰度图及采用CMA-GSO优化多阈值Otsu算法得到的二、三、四和五阈值分割结果.可见,分割阈值越大,分割得到的图像的灰度信息更加丰富,更能充分体现出原图中的目标对象.
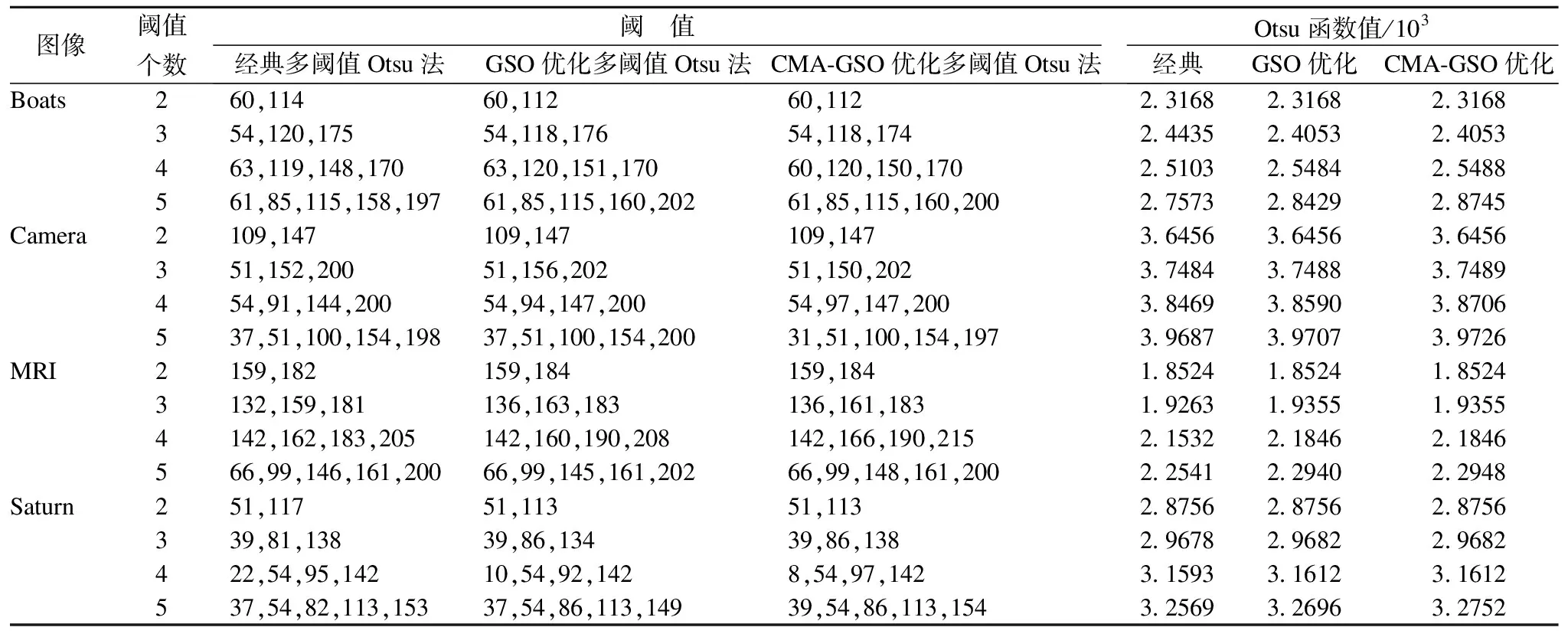
表1体现了对于复杂多目标图像的分割,在分割阈值较小时,本文方法与其余两种方法的分割精度较为一致,而随阈值的增多,本文方法分割更加精确.

图2 从左向右依次是原始灰度图,二阈值、三阈值、四阈值、五阈值分割图;从上向下依次是Boats图、Camera图、MRI图和Saturn图Fig.2 From left to right arethe picture of original grayscale map,two thresholds,three thresholds,four thresholds,and five thresholds segmentation;from top to bottom are the picture of Boats,Camera,MRI and Saturn
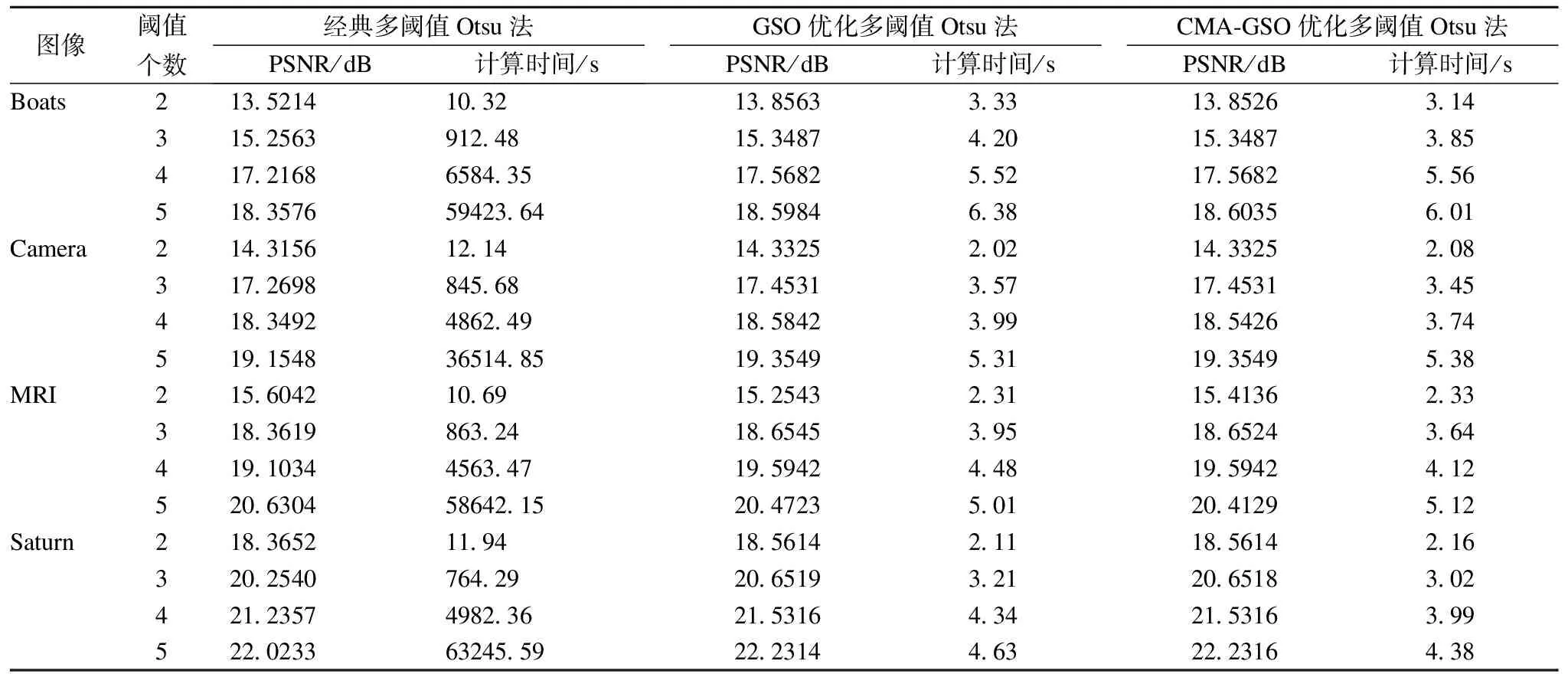
为了体现本文算法在计算时间和图像分割效果上的优越性,采用图像的峰值信噪比PSNR、计算时间来进行对比,结果如表2所示.可见本文方法在二、三、四、五阈值分割的速率分别比经典多阈值Otsu算法快5.52倍,237.01倍,1184.24倍和9887.46倍.虽然与GSO优化多阈值Otsu算法对比,本文算法的计算速率基本一样,但是本文算法的图像峰值信噪比(PSNR)值要优于GSO优化多阈值Otsu算法,说明本文算法在连续运行时分割质量较高.
表1 3种算法得出的图像分割阈值与Otsu函数值
Table 1 Segmentation thresholds and Otsu function from three methods
图像阈值个数阈 值经典多阈值Otsu法GSO优化多阈值Otsu法CMA-GSO优化多阈值Otsu法Otsu函数值/103经典GSO优化CMA-GSO优化Boats260,11460,11260,1122.31682.31682.3168354,120,17554,118,17654,118,1742.44352.40532.4053463,119,148,17063,120,151,17060,120,150,1702.51032.54842.5488561,85,115,158,19761,85,115,160,20261,85,115,160,2002.75732.84292.8745Camera2109,147109,147109,1473.64563.64563.6456351,152,20051,156,20251,150,2023.74843.74883.7489454,91,144,20054,94,147,20054,97,147,2003.84693.85903.8706537,51,100,154,19837,51,100,154,20031,51,100,154,1973.96873.97073.9726MRI2159,182159,184159,1841.85241.85241.85243132,159,181136,163,183136,161,1831.92631.93551.93554142,162,183,205142,160,190,208142,166,190,2152.15322.18462.1846566,99,146,161,20066,99,145,161,20266,99,148,161,2002.25412.29402.2948Saturn251,11751,11351,1132.87562.87562.8756339,81,13839,86,13439,86,1382.96782.96822.9682422,54,95,14210,54,92,1428,54,97,1423.15933.16123.1612537,54,82,113,15337,54,86,113,14939,54,86,113,1543.25693.26963.2752
表2 3种算法的PSNR与计算时间
Table 2 Comparison of PSNRs and computing time from three methods
图像阈值个数经典多阈值Otsu法PSNR/dB计算时间/sGSO优化多阈值Otsu法PSNR/dB计算时间/sCMA-GSO优化多阈值Otsu法PSNR/dB计算时间/sBoats213.521410.3213.85633.3313.85263.14315.2563912.4815.34874.2015.34873.85417.21686584.3517.56825.5217.56825.56518.357659423.6418.59846.3818.60356.01Camera214.315612.1414.33252.0214.33252.08317.2698845.6817.45313.5717.45313.45418.34924862.4918.58423.9918.54263.74519.154836514.8519.35495.3119.35495.38MRI215.604210.6915.25432.3115.41362.33318.3619863.2418.65453.9518.65243.64419.10344563.4719.59424.4819.59424.12520.630458642.1520.47235.0120.41295.12Saturn218.365211.9418.56142.1118.56142.16320.2540764.2920.65193.2120.65183.02421.23574982.3621.53164.3421.53163.99522.023363245.5922.23144.6322.23164.38
将使用本文所提出的算法和文献[3],文献[11]所提出的算法分别对国际公共图像测试库中的Camera图进行迭代次数从0到1000的二阈值图像分割实验,并计算二阈值分割时间和与穷举法得到的阈值相比阈值变化率,实验结果如图3所示.与文献[3]和文献[11]相比,本文所提出的算法随迭代次数的增长分割时间增长最慢,即本文所提出的算法降低了时间复杂度.并且本文所提出的算法随迭代次数的增长阈值变化率降低最快,即本文所提出的算法得到的阈值精确度高.
综上所述,本文提出的基于CMA-GSO优化算法的多阈值Otsu图像分割方法,能够有效快速并且精确地分割复杂多目标图像,并且在医学,科学等领域具有现实意义.

图3 对Camera图进行二阈值分割时,左图表示计算时间随迭代次数增长的变化曲线,右图表示阈值变化率随迭代次数增长的变化曲线Fig.3 For the two-threshold segmentation of the picture of Camera,the left graph shows the change curve of the computation time with the increase of iterations,and the right graph shows the change curve of the threshold change rate with the increase of iterations
5 结 论
本文主要针对复杂多目标灰度图像分割耗时多的缺点,提出了基于CMA-GSO优化算法的多阈值Otsu图像分割方法.首先,针对GSO算法易陷入局部最优解的“早熟”问题,联想到细胞膜算法的保留最优解策略,提出了CMA-GSO优化算法.其次,针对多阈值Otsu图像分割算法在时间复杂度上的NP难题,提出了将混合优化算法应用于多阈值Otsu图像分割,在最优阈值的搜索过程中采用自然启发式搜索而不是穷举法搜索,降低阈值搜索的时间复杂度.最后,对多目标灰度图像进行分割,并与经典多阈值Otsu算法和GSO优化多阈值Otsu算法进行比较.实验成果表明,在分割阈值数量较多时,CMA-GSO优化多阈值Otsu算法的计算速度比经典多阈值Otsu算法提高95%.同时,本文算法在分割的精确度上高于GSO优化多阈值Otsu算法.该方法已经应用于脑部切片(MRI)图,复杂风景(Boats)图,行星(Saturn)图和高对比度人物(Camera)图,并且取得了快速有效的分割结果.

