基于局部估计密度的局部离群点检测算法

谢 兄,唐 昱

(大连海事大学 信息科学技术学院,辽宁 大连 116026)

1 引 言

离群点检测技术在许多领域中都有所应用,如网络入侵检测[1,2]、欺诈检测[3]、工业损伤检测[4]等,其目的是消除噪声或发现数据中行为异常的“部分”数据.离群点集合是数据集中的一个特殊子集,在不同的领域有不同的定义,通常又被称为异常点、偏差点、噪声点等.Hawkins将离群点定义为[5]:一个离群点是一个观察点,它偏离其它观察点如此大以至于怀疑是由不同机制产生的.在早期的聚类算法和一些离群点检测算法研究中,研究对象通常是基于整体数据集,检测算法可以检测出一些全局离群点[6].然而在实际应用中,所获得的数据通常是不完整的,许多情况下只关心局部范围内数据所包含的信息,需要进行局部离群点检测.Breuing最先提出局部离群点的定义[7]:局部离群点是指在数据集中与其邻域表现不一致或偏离其邻域的观测点.已有的离群点检测算法大致可以分为:基于统计的算法[8]、基于距离的算法[9,10]、基于密度的算法[7,11-16]等.

基于统计的离群点检测算法,需要事先假设数据服从某种标准分布,如果某个数据与这个分布的偏差较大,则将其标记为离群点.但是对于不遵循任何标准分布的数据集或无法预知数据集的分布类型时,无法使用基于统计的检测算法对数据集进行离群点检测.

基于距离的离群点检测算法不需要预先知道数据的分布模型,如果数据集中某个对象与数据集中超过一定比例的其它对象的距离大于某个阈值,则将这个对象视为离群点.然而基于距离的离群点检测方法检测出的是全局离群点,没有考虑局部离群点.

基于统计的离群点检测方法与基于距离的离群点检测方法都具有一定的局限性,对于分布复杂的数据集,无法准确的检测出数据集中的局部离群点,因此研究者提出了基于密度的局部离群点检测方法[7,11-16].基于密度的离群点检测算法在判断一个对象是否属于离群点时,除了将该点与其它点之间的距离作为依据外,还增加其一定范围邻域内所包含的对象数量作为判别依据,这两个依据共同构成该对象的“密度”属性.

LOF(Local Outlier Factor)算法[7]是一种基于密度的局部离群点检测算法,这个算法不再将离群看作是一个二元属性,用局部离群因子这一概念,量化对象的离群程度,LOF算法为数据集中的每个对象赋予一个局部离群因子来表示该对象的离群程度,再进一步从离群程度较高的数据集合中寻找离群点.对于数据集中的任意一个数据对象s,首先通过给定的参数k确定其k-距离与k-邻域,并计算出数据对象s相对于k-邻域内其它数据对象的可达距离,进而计算出s的可达密度,最后用s的k-邻域内所有其它数据对象的平均可达密度与s的可达密度的比值作为数据对象s的局部离群因子.目前已经有许多学者针对不同的数据集或应用场景对LOF算法进行改进和扩展,在其基础上提出多种局部离群点检测算法.其中比较有代表性的算法有:朱利等人[11]提出基于k-近邻的最小生成树离群点检测算法,该算法先在原始数据集上构建平分树,计算数据点的k-近邻,最后计算数据的局部离群因子,进而检测出局部离群点.涂晓敏等人[12]将邻域改为方形邻域,减少邻域查询次数,降低了时间复杂度,并使用裁剪系数来代替LOF算法中的可达距离、可达密度的计算.SimplifiedLOF算法[13],该算法用k-距离代替可达距离进行局部离群因子计算,简化局部离群因子的计算过程,但检测结果的准确性受到一定影响.Su等人[14]提出使用局部偏差系数LDC来重新定义局部离群因子,这种方法通过计算数据对象与其邻域内其它对象之间距离的期望和方差来判断数据对象的离群程度.Schubert等人[16]将LOF算法与核密度估计[15]方法结合起来,提出KDEOS算法,该算法使用LOF算法中的可达距离来代替核密度估计公式中的传统距离,之后使用求出的密度估计来表示数据对象的密度.核密度估计方法可以求解给定样本点集合的分布密度函数,属于非参数估计方法.这种方法不利用数据分布的先验知识,不需要事先对数据分布做出假设.

离群点检测算法运用在交通数据去噪问题时,需要尽可能的检测出所有的离群点,以消除数据集中噪声点对后续工作的影响,即需要提高算法的查全率.针对这种情况,提出一种新的基于局部估计密度的局部离群点检测算法LOLED(Local Outlier Detection Based on Local Estimation Density),该算法利用核密度估计方法计算数据集中每个数据的局部估计密度,为了反映数据集中每个数据的局部范围内的稀疏密集程度对其密度计算结果的影响,对核密度估计方法进行优化,使带宽的值可以根据局部范围内稀疏密集程度的不同进行调整;然后用局部估计密度计算局部离群因子,利用每个数据的局部离群因子判断这个数据是否是离群点.最后在UCI标准数据集与模拟公交轨迹数据集上进行实验,验证检测算法的有效性,局部离群点检测算法的查全率提高.

2 局部离群点检测算法

LOLED算法是对LOF算法进行改进,先给出LOF算法的一些基本定义,再详细介绍LOLED算法.给定一个样本数据集S={s1,…,sn},n为样本数量,每个样本si={a1,…,am}是m维样本数据对象,si∈S.

2.1 LOF算法

LOF算法的核心思想是计算数据对象的局部可达密度,并使用其邻域范围内所有其它对象的局部可达密度的平均值与自身局部可达密度值的比值来表示该数据对象的离群程度,这个比值被称为局部离群因子,反映数据对象是否分布在与其密度较为相近的局部区域内.LOF算法的一些基本定义如下[7]:

定义1.对象si的k-距离,k-distance(si):对于任意小于n的正整数k,si∈S,对象si的k-距离,记为k-distance(si),被定义为si与sj之间的距离d(si,sj),其中sj∈S,且sj满足以下条件:

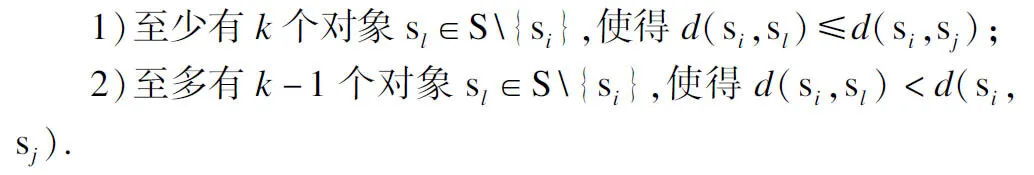
定义2.对象si的k-邻域,Nk(si):si∈S,给定si的k-距离,si的k-邻域包括数据集中所有与si的距离不大于k-距离的其它对象,即:

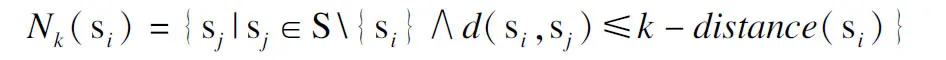
(1)

定义3.对象si相对于对象sj的可达距离,reach-distk(si,sj):给定自然数k,且si,sj∈S,对象si相对于对象sj的可达距离被定义为:

reach-distk(si,sj)=max{k-distance(sj),d(si,sj)}

(2)

定义4.对象si的局部可达密度,lrd(si):si∈S,对象si的局部可达密度被定义为:

(3)

定义5.对象si的离群因子,LOF(si):si∈S,对象si的局部离群因子被定义为:

(4)

LOF算法在求出数据集中每个数据对象的局部离群因子后,对这些值进行排序,输出排序后离群因子较大的z个数据对象作为数据集S的离群点集合,其中z值是根据不同数据集规模给定的参数.

2.2 基于局部估计密度的局部离群点检测算法

LOLED算法首先使用核密度估计方法求出每个数据的局部估计密度,并在计算过程中引入了每个数据的k-邻域信息;再利用每个数据的局部估计密度与其k-邻域内其它数据的局部估计密度,计算出每个数据的局部离群因子;最后将每个数据的局部离群因子与某个固定的阈值进行比较,进而判断出该数据是否属于离群点.

2.2.1 局部估计密度的计算

核密度估计方法可以在未知数据集分布模型的情况下,利用数据自身的信息,估计未知的密度函数,进而计算出每个数据的估计密度.首先给出标准核密度估计公式[15]:

(5)

其中‖si-sj‖表示两个对象之间的距离,‖si-sj‖=d(si,sj).h(sj)是一个平滑函数,也称为带宽.带宽函数h(sj)的最简单选取方式为h(sj)=h,即固定带宽.但对于真实数据集来说,不同数据间的局部密度可能存在差异,固定带宽不能很好的适应这种情况,需要一种可以适应不同数据密度的方法,因此在带宽函数中引入尺度参数.对于任意两个数据对象si,sj,其距离为d(si,sj),设尺度参数为σ,可以通过比较d(si,sj)与σ来判断两个对象间的相似性,若d(si,sj)≤σ,则两个对象间的相似度较高,若d(si,sj)>σ,则两个对象间的相似度较低.当数据集中存在多个密度不同的簇时,全局尺度参数无法很好的衡量两个对象间的相似情况,因此引入局部尺度参数,即在比较密集的簇内,尺度参数的设置偏小,而对于较为稀疏的簇,尺度参数的设置偏大,尺度参数的大小可以根据数据自身的分布情况进行调整.引入k-邻域平均距离来衡量对象所处区域的稀疏或密集情况:

定义6.对象si的k-邻域平均距离,Nk-adist(si):对象si的k-邻域平均距离定义为:

(6)

期望值往往可以反映出特定属性空间中数据的整体分布情况.Nk-adist(si)是数据对象si的k-邻域内的所有其它对象到si距离的平均值,可以很好的反映出对象si与其k-邻域Nk(si)整体的偏离程度,根据密集区域的数据对象的k-邻域平均距离较小、稀疏区域的数据对象的k-邻域平均距离较大的特点,可以设置局部尺度参数为:

σi=Nk-adist(si),σj=Nk-adist(sj)

(7)

并进一步设置带宽函数为:

(8)

这种计算方式将样本点的邻域信息,即数据对象的k-邻域平均距离引入到带宽函数计算中,使得带宽可以根据不同样本点邻域的稀疏密集情况进行自动调整.

公式(5)中的K是满足积分为1,期望为0,带宽为h(sj)的m维函数,选择高斯核函数作为核密度估计的内核函数,其公式为:

(9)

由于所要检测的离群点为局部离群点,只需考虑样本点周围一定范围内的数据分布情况,因此将公式(5)中的求和范围限制在样本的k-邻域范围即可,将公式(8)、公式(9)代入到公式(5)中,可以获得数据样本si的局部估计密度led(si),计算公式为:

(10)

公式(10)可以进一步优化为:

(11)

2.2.2 基于局部估计密度的局部离群因子计算

求出给定数据点的密度估计后,不能仅使用估计值来判断该点是否为离群点.交通数据分布往往是多密度的,同一数据集中可能存在多个簇,属于不同簇的数据可以具有不同的密度.当数据集中的某个簇较为稀疏时,属于这个簇的数据会具有较低的密度,但这些点不应被判定为离群点.参考定义5,利用某个数据点si的局部密度估计与其k-邻域范围内所有其它点sj(i≠j)的局部密度估计的平均值,可以计算出si的局部离群因子LOLED(si),计算公式为:

(12)

理想情况下,LOLED(si)的值越接近于1,表示数据对象si与其k-邻域的平均局部密度越接近,si与其邻域属于同一簇的可能性越大.如果这个值小于1,说明数据对象si的局部密度大于周围的密度,si为密集点,si为离群点的可能性较小;如果这个值大于1,说明数据对象si的局部密度小于周围的密度,si是离群点的可能性较大.实际情况中,阈值的确定与数据规模和实际待解决的问题有关,通常阈值o取值大于1.

2.2.3 LOLED算法描述

可以通过设置局部离群因子阈值o,来判断数据集中的数据点是否为离群点,如果数据对象的局部离群因子大于阈值,则判定为离群点;如果数据对象的局部离群因子小于阈值,则判定为正常点.详细的LOLED算法描述如下:

输入:具有n个m维数据对象的数据集S;邻域范围k;局部离群因子阈值o

输出:数据集S的离群点集合O

1. for each s in S

2. 构建数据对象s的k-邻域集合Nk(s);

3. 根据公式(11)计算数据对象s的局部估计密度led(s);

4. 根据公式(12)计算数据对象s的局部离群因子LOLED(s);

5. ifLOLED(s)>o

6. 将数据对象s添加到离群点集合O中;

7. end if

8. end for

9. 输出离群点集合O

3 实验验证

3.1 UCI数据集实验结果与分析

UCI数据库是一个常用的标准测试数据集,经常用来验证算法的有效性.由于数据集中的离群点是未知的,参照文献[17]中的方法,对UCI数据库中的3个数据集进行处理,删除数据集中某一类的大部分数据,只保留小部分数据,保留下来的这些数据偏离其它的数据点较远,可以作为待检测的离群点,其它类的数据则当作正常点.处理后最终得到6个测试数据集如表 1 所示, 其中离群点数量为删除类在删除大部分

表1 UCI数据集处理结果
Table 1 UCI datasets process result

数据集编号数据集删除类离群点数量剩余总数据点数量1IrisIris-setosa51052IrisIris-versicolor51053Glass5651924Glass6751865Ionosphereg151406Ionosphereb15240

数据后剩余的数据点个数,剩余总数据点数量是离群点数量与正常点数量之和.

实验分别采取LOLED算法、SimplifiedLOF算法、LOF算法与KDEOS算法对6个处理后的数据集进行局部离群点检测.将正确检测出的离群点的数量设为TP,正常点检测为离群点的数量设为FP,离群点检测为正常点的数量设为FN,4种算法的检测结果如表2所示.

表2 4种算法在UCI数据集上的检测结果
Table 2 Detection results of the four algorithms
on UCI datasets

数据集编号LOLEDSimplifiedLOFLOFKDEOSTPFPFNTPFPFNTPFPFNTPFPFN159021635704912510038221133723521033248151804417136236341515923651610931662396112647198102459276

选择查准率、查全率与F-Measure作为算法的评价指标.查准率,也称精确率(precision),记为P,计算公式为:

(12)

查全率,也称召回率(recall),记为R,计算公式为:

(13)

查准率和查全率呈负相关,一般来说,查准率高时,查全率通常偏低,而查全率高时,查准率通常偏低.F-Measure,记为Fβ,是查准率和查全率的加权调和平均,是一个常用的评价标准,计算公式为:

(14)

其中β为参数,不同的应用中对查全率和查准率的要求有所不同,可以通过对β设置不同的值来调整对查准率或查全率的偏好,当β>1时查全率有更大影响,β<1时查准率有更大影响.实验中取β=1,即:

(15)

文献[18]指出,k值的选取与数据规模无关,实验过程中,当参数k=9时,四种算法都可以在各个数据集上取得较好的效果,包括维数较高的数据集.阈值o的选取与实际的需求有关,阈值o越大,算法检测出的离群点个数越少,即TP+FP的值越小,o的取值通常应大于等于1.图1列出在k=9的情况下,阈值o分别取值为1.0、1.3、1.5、1.7时,四种算法在不同数据集上的F-Measure值的平均值.

由图1可知,KDEOS算法、LOF算法与LOLED算法在阈值o=1.3时,具有最高的平均F-Measure值,即算法的表现最好,因此后续实验设置参数为k=9,o=1.3.表3、表4、表5分别列出四种算法在UCI数据集上的查准率、查全率与F-Measure的比较结果.表3显示,LOLED算法的查准率与其它算法的查准率在不同数据集上比较结果有所不同.表4中,LOLED算法的查全率在6个数据集上都高于或等于其它算法的查全率.表5显示,LOLED算法与其它算法的F-Measure在不同数据集上有不同的比较结果.

图1 四种算法不同阈值时的F-Measure比较Fig.1 F-Measure comparison of four algorithms with different thresholds

表3 四种算法在UCI数据集上的查准率结果
Table 3 Precision of the four algorithms on UCI datasets

数据集编号LOLEDSimplifiedLOFLOFKDEOS135.71%11.11%41.67%30.77%233.33%27.27%15.38%30.00%319.23%50.00%33.33%21.74%419.05%33.33%33.33%21.05%528.13%23.81%22.50%20.69%629.73%26.92%29.41%25.00%

3.2 真实数据集

为了验证LOLED算法在真实数据集中的有效性,实验模拟某市公交车轨迹数据进行模拟测试.公交车配备的GPS设备在记录移动对象的位置信息时,由于GPS设备的精度问题、GPS系统的自身误差、司机休息时没有关闭GPS设备等原因,会产生一些离群数据.这些数据所包含的位置信息明显不同于其它的数据对象,被视为噪声点,这些噪声点对基于公交轨迹数据的城市路网提取、交通流量预测等后续工作产生较大影响,在数据预处理阶段需要进行去噪,即对原始数据集进行离群点检测并剔除离群点.实验模拟两组单向行驶的轨迹数据进行实验,并计算出数据集中每个数据点与已有路网信息的道路中心线的距离,将与道路中心线距离大于7米的数据点看作是离群点.第一组为直线路段的数据,原始GPS数据点数量为500个,计算后得到第一组数据的离群点个数为68个,数据的原始GPS点分布如图3(a)所示.第二组为交叉路口区域的数据,原始GPS数据点数量为1100个,计算后得到第二组数据的离群点个数为136个, 数据的原始GPS点分布如图3(b)所示. 轨迹数据的数据量较大,正常点的分布极为密集,在进行离群点检测时,注重去除离群点,以削弱离群点对后续工作产生的影响,需要较高的查全率.

表4 四种算法在UCI数据集上的查全率结果
Table 4 Recall of the four algorithms on UCI datasets

数据集编号LOLEDSimplifiedLOFLOFKDEOS1100.00%40.00%100.00%80.00%2100.00%60.00%40.00%60.00%3100.00%60.00%80.00%100.00%480.00%60.00%50.00%80.00%560.00%33.33%60.00%40.00%673.33%46.67%66.67%60.00%

表5 四种算法在UCI数据集上的F-Measure结果
Table 5 F-Measure of the four algorithms on UCI datasets

数据集编号LOLEDSimplifiedLOFLOFKDEOS152.63%17.39%58.82%44.44%250.00%37.50%22.22%40.00%332.26%54.55%47.06%35.71%430.77%42.86%40.00%33.33%538.30%27.78%32.73%27.27%642.31%34.15%40.82%35.29%

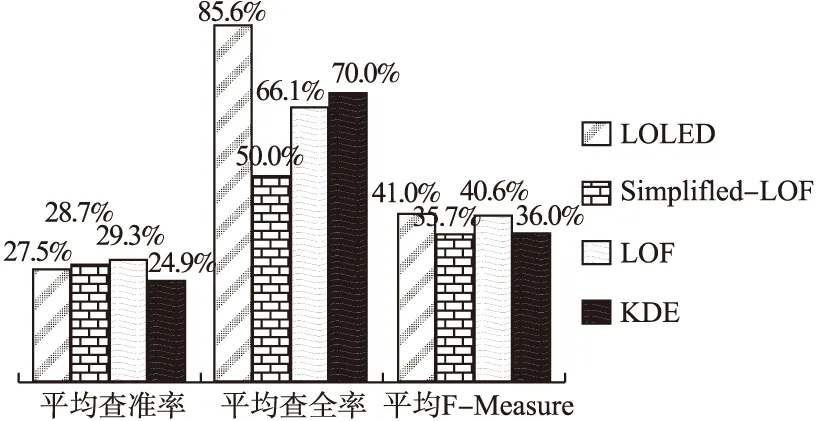
图2 四种离群点检测算法的表现对比图Fig.2 Performance comparison of the four algorithms

图3 某市公交车模拟轨迹数据点Fig.3 Synthetic bus trajectory data of a city

实验分别选取LOLED算法、SimplifiedLOF算法、LOF算法、KDEOS算法对两组数据进行处理,设置参数k=9,同时考虑实际业务需求,为了避免检测出过多的离群点,导致GPS数据集剔除掉检测出的离群点后,剩余的点无法看出轨迹形状或轨迹出现缺口等现象,将阈值o设为较大的值,设o=1.5,四种算法在两组数据集上的检测结果如表6所示,表7、表8、表9分别列出四种算法在模拟数据集上的查准率、 查全率与F-Measure的比较结果.两组GPS数据检测结果可视化后分别如图4、图5所示,其中较小的点表示检测出的噪声点,较大的点表示检测出的正常点.图4(b)(c)(d)与图5(b)(c)(d)中方框内较大点的数量明显多于图4(a)与图5(a)中相应位置上较大点的数量,这些点虽然被检测为正常点,但从图中可以看出,方框内的较大点应属于噪声点.

表6 四种算法在模拟数据集上的检测结果
Table 6 Detection results of the four algorithms
on synthetic datasets

数据集LOLEDSimplifiedLOFLOFKDEOSTPFPFNTPFPFNTPFPFNTPFPFN直线路段598893247364360254910419交叉路口119196177212764961524010421232

表7 四种算法在模拟数据集上的查准率结果
Table 7 Precision of the four algorithms on synthetic datasets

数据集LOLEDSimplifiedLOFLOFKDEOS直线路段40.41%40.51%41.75%32.03%交叉路口36.84%36.18%38.71%32.91%

表8 四种算法在模拟数据集上的查全率结果
Table 8 Recall of the four algorithms on synthetic datasets

数据集LOLEDSimplifiedLOFLOFKDEOS直线路段86.76%47.06%63.24%72.06%交叉路口87.50%52.94%70.59%76.47%

表9 四种算法在模拟数据集上的F-Measure比较结果
Table 9 F-Measure of the four algorithms on synthetic datasets

数据集LOLEDSimplifiedLOFLOFKDEOS直线路段55.14%43.54%50.29%44.34%交叉路口51.85%42.99%50.00%46.02%

图4 四种算法在第一组数据集的实验结果Fig.4 Experimental results of the four algorithms on the first data set

综合表7、表8、表9的内容可以看出,LOLED算法的查全率较高,虽然算法的查准率较低,但原始的GPS数据经过离群点检测,并剔除离群点后,图3(a)、图4(a)中剩余的点依然可以看出道路骨架的形状,偏离其它大部分数据、游离在道路外的点已经被识别并剔除.其它算法存在的漏判较多,处理后的数据中漏判的离群点对后续工作的影响仍然较大,LOLED算法的漏判情况则较少,基本消除后续工作中离群点的影响.LOLED算法具有较高的查全率,在模拟数据集中,也可以取得较好的效果.

图5 四种算法在第二组数据集的实验结果Fig.5 Experimental results of the four algorithms on the second data set

4 结 论

LOLED算法将核密度估计方法引入到局部离群点检测算法中,用核密度估计方法计算出的密度估计,来代替传统LOF算法中的局部可达密度,并使用局部尺度参数来代替传统高斯核函数的固定带宽,可以更好的适应密度不均匀、形状不规则的数据集.在实验方面,利用UCI标准数据集与模拟数据集,验证算法的有效性,其中查全率有明显改善.在实际应用中也可以取得较好的效果.下一步将重点研究算法的最优参数选择方法以及进一步提高算法的查准率.