基于Spark框架的用于金融信贷风险控制的加权随机森林算法
胡婵娟,于莲芝,薛 震
(上海理工大学 光电信息与计算机工程学院,上海 200093)
1 引 言
随着金融业以及互联网业的快速发展,互联网金融作为一种新兴的商业模式逐渐走进大家的视线.中小额贷款等互联网金融的线上业务量也随着互联网规模的增长在快速增加.个人、商家乃至企业的贷款与申请逐渐走向快速化和无纸化.在早期,贷款违约预测完全依赖人工审核.这种预测方式只适合小规模的信用审核,而对大规模的贷款审核无能为力[1].为解决人工审核过程中人为因素的不确定性,一种依据详细规则来判断是否进行贷款的方法被金融机构提出.该方法根据规则给出结论,使信审员可以根据清洗的指标来判断是否放款.同时该方法的提出极大降低了对信审员的要求,普通职员经过相关的培训即可着手信贷工作.此外,国内外众多研究学者提出数据挖掘的模型对信贷违约进行了研究[2-7].
Spark是基于Hadoop生态实现的基于内存的分布式计算框架.该框架诞生于UC Berkeley AMPLab,整个发展过程都沉浸在学术氛围里,近年来一直处于高速发展期.2010年Chowdhury M与Zaharia M等人提出Spark的雏形——集群计算工作集[8];2012年Zaharia M等人又提出了弹性分布式数据集的概念[9];文献[10]基于分布式平台Spark对数据挖掘算法的并行化进行了研究,该研究由梁彦完成;文献[11]中刘泽燊等人提出适用于分布式环境下的基于Spark平台的支持向量机算法(SP-SVM);文献[12]中邵梁等人针对大数据中的频繁项集挖掘问题,提出了一种基于Spark框架的FP-Growth频繁项集并行挖掘算法.在对随机森林算法的研究上,自1995年贝尔实验室的Ho TK首次提出了随机森林的概念开始[13],大量学者对该算法及其应用进行了研究[14-18].
本文设计并实现了基于Spark分布式计算框架的适用于金融信贷风险控制中的加权随机森林算法.传统决策树算法虽然简洁有效,但是在面对数据过拟合的问题上一直表现不佳.而随机森林通过引入随机性,最大程度上减小了过拟合问题的出现.使用SMOTE算法能够很好的应用于风险控制分类,不但较好的解决了数据集的非平衡性问题,而且保留了原有数据集的信息.而作为大数据分析系统,本文通过构建Spark分布式系统对模型并行化的方式,极大提高了效率性与时效性.
2 相关技术及方法
2.1 Spark分布式框架
Spark的最根本特性是它的基于内存运算技术能够减少对硬盘的I/O操作,数据可以直接在内存进行分析运算.在Hadoop的MapReduce计算引擎需要把计算的中间值先存放在内存,然后等到下一步计算的时候重新向外存发起I/O请求.Spark则会把中间值直接存放到内存中进行迭代,因此Spark与传统的MapReduce的整体相比减少了数据传送的时间,进而保证了任务的运行效率.
Spark作为基于内存计算的分布式计算引擎,它的核心是由引擎定义的弹性分布式数据集(RDD,Resilient Distributed Datasets),RDD就是Spark引擎操作的基本数据结构.如图1所示表示Spark的体系结构图.
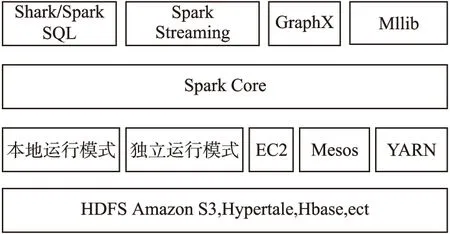
图1 Spark的体系结构Fig.1 Architecture of Spark
Spark的核心模块叫做Spark Core,基于RDD的Dataframe的核心模块通过有向无环图进行任务规划,从而使Spark在批处理任务时具有灵活性.在Spark Core的基础上,各种大数据处理解决的方案也应运而生.例如利用Spark轻量级调度优势从而实现流处理模式的Streaming;图形计算框架Graph;实现机器学习的Mllib机器学习库;提供分布式SQL查询的Shark.
Spark和很多分布式文件系统都要很好的兼容性,HDFS和Amazon S3系统都是常用的Spark分布式文件系统.它的运行模式分为单点模式和分布式模式,分布式模式可以使用YARN,Mesos或者EC2进行资源分配与调度.Spark计算框架围绕着整个RDD进行并行计算,基于内存的运行特性,使得Spark的计算效率大大提高.RDD作为具有容错的、并行特性的数据结构,能够灵活的在内存和外存上进行交互.当内存已经满足不了单个RDD的需求时,RDD会转存到外存上:与此同时,RDD作为Spark的只读数据结构,如果发生了RDD数据丢失,那么只能利用相应的容错机制重建RDD.
2.2 随机森林算法
2.2.1 传统的随机森林算法
随机森林算法是一种使用多个基分类器——决策树,来学习和预测样本的集成模型[19].其具体工作原理如下:
1)通过在原始数据集上有放回的抽样选取n个样本形成一个新的训练子集;
2)在步骤1生成的子数据集上对所有的特征进行抽样,选取m个特征成为决策树的分离节点,并且该决策树不进行剪纸操作;
3)重复步骤1与步骤2,直到得到具有s颗决策树的集合;
4)将新样本交由步骤3 得到的决策树集合中的每棵树进行预测,记录每一个决策树的预测类别并统计总数,最后总数最多的一个类别就是模型选择的最佳结果.
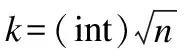
2.2.2 加权随机森林算法
随机森林算法虽然在数据挖掘中能够取得非常优异的表现,但是该算法对非平衡数据进行训练时的准确度下降和性能下降一直是该算法的应用局限.解决这种非平衡性的简单方法就是利用数据挖掘软件Weka中的方法,直接选取首个类别作为最后的结果,但是这种方法并不能根本解决平局问题,而权值计算则可以有效避免这种因无法处理平局情况导致模型构建陷入停滞问题.
针对传统随机森林算法带来的问题,本文提出了如下改进措施.基本思路为:
1)在投票之前根据决策树的分类性能每棵决策树赋予一个权重;
2)当获得决策树的分类结果后,将相应的分类结果乘以决策树的权重;
3)统计所有乘以权重之后的投票结果,并进行降序排列,选择最终权值最高的类别作为最后分类的结果.
由此可见决定最终分类结果的关键在于权重的分类方式,但是如果给分类能力强的决策树高的权重,则会导致分类能力差的决策树无法发挥自身价值,让整个随机森林忽视了低分类能力决策树的分类结果,这就违背了随机森林算法所基于的Bagging算法.所以模型的建立需要遵循不影响公平的情况下提高正确度的原则.
在参考文献[14]中,作者通过研究贝叶斯公式来评价每个分类器的分类性能优劣.最后推出公式(1).
(1)
在公式(1)中,N表示分类器的总数,con(k)表示Bagging算法中第k个分类器的分类结果后验概率,weight(i)表示第i个分类器的权重.
文献[14]中作者证明了该公式的两点性质:
1)分类正确率越高对应的决策树权重越高;
Bagging算法可以通过out-of-bag数据进行分析,而且out-of-bag的F1值要比Bayes公式通过计算后验概率计算分类难度更小.因此为了降低计算量,放弃使用分类结果的后验概率而使用out-of-bag的F1进行判断分类的正确率,本文对公式(1)进行修改得到公式(2):
(2)
公式(2)中N表示分类器的总数,oobF1(k)表示第k个分类器的out-of-bag的F1值,weight(i)表示第i个分类器的权重.
与一般的算法在投票之后选择如何评判相同票数的决策树不同,加权算法从投票完成的时候就已经极大的减少了平局现象发生的概率.通过计算发现,当权重值保留的小数位数越多,出现平局的概率就越小.因此在不影响模型建立时间的基础上,尽可能多的保留小数位数成为了防止平局出现的最直接手段.
3 Spark的并行加权随机森林算法分析与设计
3.1 加权随机森林的并行优化策略
由于数据集抽样的随机性和节点特征分裂的随机性,保证了决策树的建立之间没有耦合性,因此作为集成学习算法的随机森林算法具有原生并行性.随机森林算法的并行化优化体现在决策并行化、节点并行化和特征选择并行化上.对随机森林算法的并行化,能够保证计算过程中数据集通过HDFS分布式文件系统部署到多个计算机节点.较在单机环境下节省了大量的I/O操作,同时避免了大量的网络带宽的占用.
通过对MapReduce计算引擎的并行数据挖掘算法库Mahout和基于单机模式的数据挖掘算法库Weka的分析.本文根据上文总结的对加权随机森林算法并行化的思路和Spark分布式计算框架的基本特点,设计了对加权随机森林算法的并行化构思与实现的方法.
3.1.1 特征切分点抽样统计
在对决策树的非叶子节点进行最优特征挑选时,需要对所选特征进行切分点的选择才可以进行计算.利用数据的分布性,在每个节点处对特征数据进行抽样统计后汇总在主节点上.该操作把所有的计算过程和I/O过程交由每个节点自主进行,但是只在最后汇总的时候占用极小的带宽,因此避免了对全量特征进行取值并排序过程占用大量的带宽和I/O操作.虽然抽样统计的做法必然会带来数据精度上的损失,不过在设置了合理的抽样数量后可以在不过分牺牲精度的前提下大大提高计算速度.
3.1.2 逐层训练
将决策树构建在单机模式下的深度优先策略转变为广度优先策略就是逐层训练的本质.在分布式环境下构建逐层训练即逐层构建树节点,构建过程中需满足遍历次数等于树的最大层数.同时在遍历过程中,只需要计算非叶节点的分割点统计参数并根据特征划分来决定是否切分以及如何切分.
3.2 加权随机森林训练的并行化
根据Spark计算引擎的特点和常规并行化流程,结合之前对加权随机森林算法的改进点分析,本文将加权随机森林算法的并行化训练分成四个主要步骤:
1)利用随机抽样获取分布在节点上的样本的特征并进行特征分箱操作;
2)利用每棵决策树的RDD构建基于特征子空间和Bagging抽样的并行化随机森林;
3)通过预测out-of-bagging数据获取每颗决策树的F1值;
4)将步骤3中生成的决策树进行耦合成一个完整的并行化加权随机森林模型.
图2为加权随机森林算法并行化训练的流程图,它描述了加权随机森林并行化的整体框架和运行步骤.
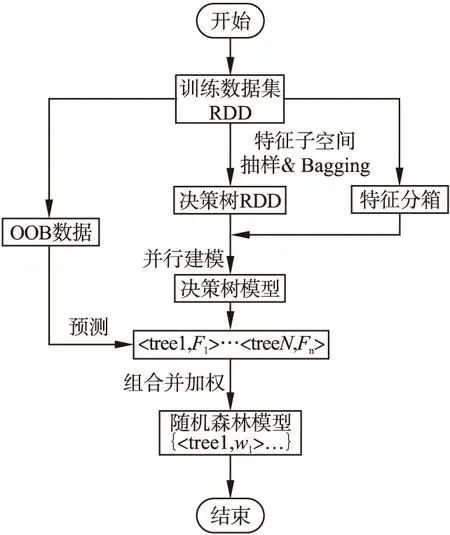
图2 随机森林并行化建模Fig.2 Model of random forest parallelization
3.2.1 特征分箱
由于随机森林有多棵树,因此在不同决策树随机选择到相同的特征时,会出现重复计算分割点的情况,导致算法的效率下降.本文先通过对数据集中所有的特征进行分箱并找出切分点,然后在所有决策树建模过程中利用之前分箱得到的切分点直接进行分类.该方法可以有效提高算法效率.
特征分箱的本质是分析所有特征的变量范围,然后找到并记录相应类别分割点.特征分箱针对不同类型的特征采用适合的策略寻找分割点,特征点可以分为三个类别:无序离散特征、有序离散特征和连续值特征.无序离散特征的划分方式为splits=2numBOXES-1-1;有序离散特征的划分方式为splits=numBoxes-1;连续特征则采用随机抽样的方式来寻找分割点.以上公式中的numBoxes为特征值可取值的个数.与此同时,为了避免因采样量过小导致采样的数据无法正常覆盖重要特征,从而导致特征分箱的过程无法进行的情况,需要在特征分箱前判断计算总样本和采样率的乘积.在本文中采取如果乘积大于10000,就选择抽样采样的策略;如果小于则选择全样本采样的策略.
下一步得到经过各个区采样后的RDD数据.如果采样量足够大,则通过每个RDD进行抽样统计;如果采样量不够大,则将每个RDD进行全量统计,对统计结果需先判断该结果对应的相应特征属于什么类型的值,然后采用相应的方法找到分割点.
3.2.2 每棵决策树的建模过程
对决策树的建模,先利用特征子空间抽样和Bagging获取相应决策树的RDD数据集,接下来对单棵决策树进行逐层训练.在这个过程中,利用先入先出队列(First Input First Output,FIFO)将在每一个分裂节点得到的RDD数据集加入队列,直到该队列为空时整个决策树训练完成.
3.2.3 随机森林中每棵决策树加权过程
权重的计算是通过out-of-bag的F1值进行衡量.得到所有k棵树的out-of-bag的F1值之后,利用公式(2)进行赋权——计算出每棵树对应的权重weigth(i),把这些决策树组合起来便是加权随机森林.图3为加权过程的流程图.
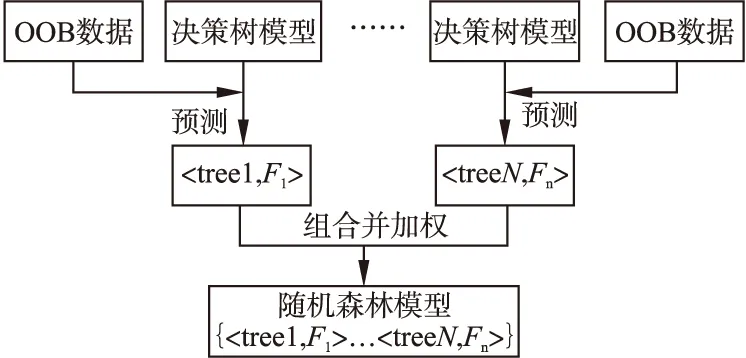
图3 加权过程Fig.3 Weighted process
3.3 加权随机森林的投票并行化
在单机模式的传统随机森林算法中,对于构建好的模型需要用新的样本进行测试并通过投票获取最后的类别.但是这个过程是串行运行的,需要随机森林中的每一棵树依次进行投票和统计.针对该情况,在面对数量较多的决策树时,对整个随机森林模型的投票过程进行了并行化.图4是对加权随机森林并行化投票的流程图.
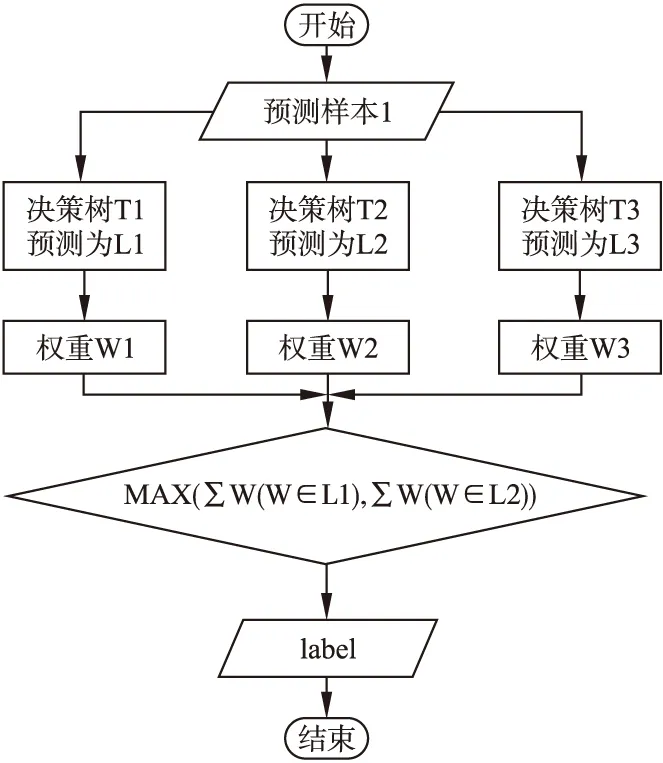
图4 加权随机森林并行化投票流程图Fig.4 Voting flow chart of weighted random forest parallelization
传统随机森林的投票过程由于一些劣质树的干扰导致最后的分类结果不好,所以为优化这一现象,本文使用out-of-bag数据的正确率作为权重依据的投票策略来代替单纯依赖相同权重的决策树投票.
4 实验结果与分析
4.1 实验相关环境及配置
该实验在中的各并行框架均搭建在Spark集群的环境下,实验过程中的存储由Hadoop进行,实验中数据的计算由Spark程序负责.在该实验过程中应用到的各开发程序及其版本号如表1所示.
表1 实验环境参数
Table 1 Experimental environment parameters

开发程序版 本操作系统Centos 7.3JDK1.8.0-144网络2GBHadoop2.7.0Spark2.12.4Master节点4核,硬盘256G,8G内存,一个节点Worker节点1核,硬盘250G,2G内存,五个节点
4.2 数据集结构化分析
该风险控制系统研究的数据来自上海某小额贷款公司2016年6月到2017年2月的业务相关数据.经过相应的清洗和采样工作,分析出数据集具有包括用户信息、信征记录、借款历史信息、互联网交易信息、社交个人信息在内的87个特征.该公司的主要业务是利用信用卡和借记卡进行7天-21天,金额1000元-5000元的小额贷款业务.在实验采样的相关月份里,根据业务量的增长,用户的贷款数据呈现一个比较快的上涨趋势,其中逾期率一直控制在百分之十左右.基于业务客观需求分析,客户违约的特征作为类别的label,按时还款用户该类置0,逾期还款用户该类置1.
4.3 评估方法及标准
针对该加权随机森林模型应用的场景,对该模型的基本性能进行评估采用以下四个结果属性分析性能指标:
1)True Positive(真正,TP):将正样本预测为正样本,即判断为真的正确率.
2)True Negative(真负,TP):将负样本预测为负样本,即判断为假的正确率.
3)False Positive(假正,FP):将负样本预测为正样本,即误报率(Type I error).
4)False Negative(假负,FN):将正样本预测为负样本,即漏报率(Type II error).
图5结了所有属性之间的数学关系
根据分类模型结果验证得到的结果属性,通过混淆矩阵的指标进行模型性能评估,表2为混淆矩阵.
表2 混淆矩阵
Table 2 Confusion matrix
混淆矩阵的评估指标分为精确率(precision)和召回率(recall).
精确率:
(3)
召回率:
(4)
除此之外还有F1值,它是精确率和召回率的调和值,F1值定义为:
(5)
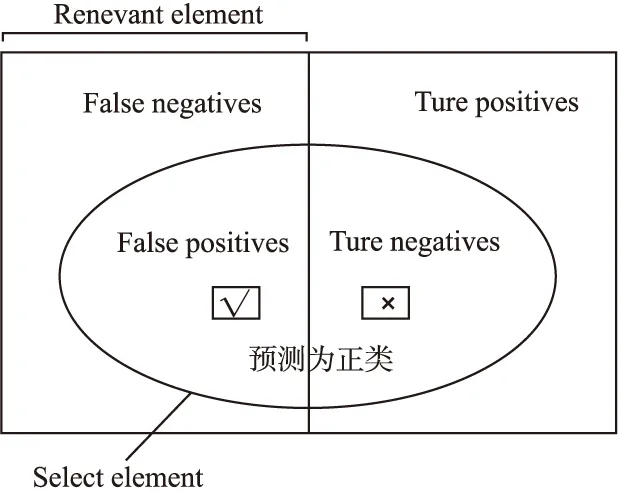
图5 分类结果示意图Fig.5 Schematic diagram of classification results
4.4 参数设置和模型优化
该模型构建构建过程中分别对随机森林算法的分裂决策(splitStrategy)、决策树的数量(numDecisionTrees)、特征数(characteristicNumberStrategy)、类别数目(ClassNumber)、决策树最大的深度(maxDepth)、决策树权重(treeWeigth)、特征分箱的最大值(maxBoxes)这7个关键参数进行调优.该模型采用Gini[22]系数作为splitStrategy的分裂标准;对小额贷款的预测分为按时还款和逾期两种,类型对应的值为别为“0”和“1”,故ClassNumber的值设置为2.对maxBoxes、maxDepth、numberDecisionTrees、characteristicNumberStrategy这四个参数的设置按照贪心算法,选取F1值作为主要评估标准,依次找到每一个参数取值范围内的最优解二次调优后得到模型最优解为:

(6)
根据公式(2)可发现treeWeigth和out-of-bag数据上的F1值成正比,为验证treeWeigth的合理性,选择200棵决策树的权重值.图6其权重图.
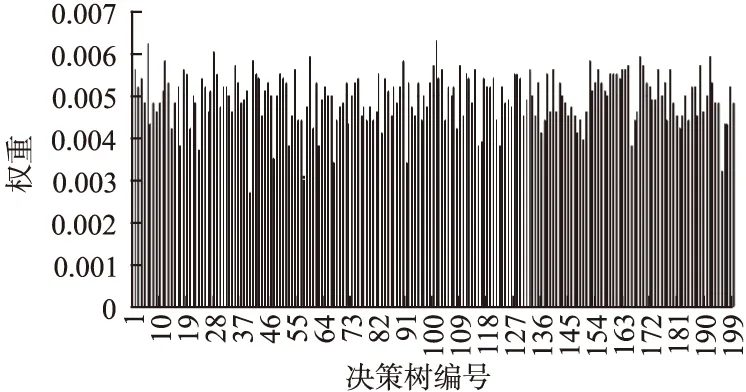
图6 加权随机森林的决策树权重图Fig.6 Decision tree weight graph of weight random forests
为验证加权过程能有效减少平均现象的产生,在考虑权值精度对平局现象影响的条件下,对包含30万个样本的数据进行不同加权策略下平局情况统计,结果如表3所示.
表3 决策树生成平局统计
Table 3 Decision tree generating tie statistics

不加权加权(权值取小数点N位)保留三位小数点保留四位小数点保留五位小数点平局情况2674880
将参数treeWeight在两次测试中设置为0与1,分别对应了不加权随机森林和加权随机森林.实验结果表明:加权随机森林的准确率为66.27%,召回率为60.97%,F1值为64.08%;不加权随机森立的准确率为64.18%,召回率为58.99%,F1值为61.80%.由此可知加权随机森林具有更好的分类能力,验证了对随机森林进行加权设计的有效性.
4.5 数据采样算法策略对比
为了有效较少非平衡数据集导致模型训练结果有效性下降的现象,该实验采用对多数类进行欠采样和对少数类进行过采样的方式生成一个相对平衡的数据集.训练数据集样本采集2017年6月-8月的总计30万条数据,经过分析发现经采样后多数类与少数类的比例由原始数据的9∶1减少为11∶3,有效降低了数据集的非平衡性.表4是采样后的数据集与未经过采样的数据集性能对比.
表4 实验样本采样效果对比
Table 4 Comparison of sampling effect of experimental samples

训练集测试数据集验证数据集准确率(%)召回率(%)F1值(%)准确率(%)召回率(%)F1值(%)未经采样35.8241.0138.2031.0135.2433.09综合采样52.5867.4759.1136.8639.7738.26
4.6 生产环境测试
对搭建的模型经过多次调优后,对数据集中的2016年9月-2017年2月的数据进行验证对比,得到了未使用模型与使用模型后的逾期率对比,如图7所示.
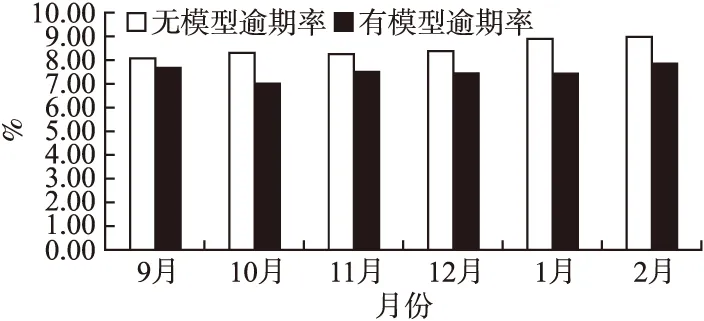
图7 未使用模型和使用模型逾期率对比Fig.7 Comparison of overdue rate between unused model an used model
在使用模型后可能由于模型规则严格导致放款金额下降,进而导致业务量降低利润下降,所以需对比在使用模型规则后的放款金额与使用前放款金额的对比,观察模型与放款金额的关系,两者对比如图8所示.
图8表明在使用模型后放款金额的量略有下降,随着放款金额的增加,有模型放款金额与无模型放款金额的比例维持稳定,没有造成业务的明显下降.
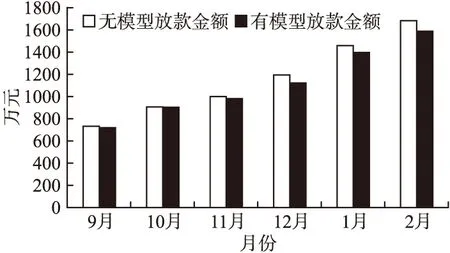
图8 无模型放款金额与有模型放款金额对比Fig.8 Comparison between unused model loan amount and used model loan amount
5 总 结
本文设计了一种基于决策树加权的并行化随机森林的分类算法.主要工作如下:设计了一种基于决策树的加权的随机森林算法;针对非平衡数据数据集在机器学习过程中的过耦合现象,利用SMOTE先对少数类进行重复采样,再对多数类进行单边采样,从而使重构后的数据趋于一个平衡的数据集;实现了基于Spark并行计算框架的加权随机森林模型,成功实现了模型的并行化.

