理性背叛的推荐合作激励机制
金 星,李明楚,孙晓梅,郭 成
(大连理工大学 软件学院,辽宁 大连 116620)
1 引 言
近年来,随着互联网和移动网络的飞速发展,基于网络合作的协作系统已大量出现在了我们的生活中.在这类系统中,虽然每一个个体的能力都是有限的,但是通过个体之间的合作行为,人们可以实现一系列复杂困难的任务.然而,由于个体理性的存在,参与者往往会选择背叛行为,从而造成了合作困境.一个典型的例子就是P2P文件共享系统里用户的搭便车现象[1].
为了促进用户的合作行为,保证协作系统的有效运行,引入激励机制已经成为了必不可少的选择.通过研究之前的文献,可以发现:在考虑策略花费这一实际场景下,互惠策略会占优无条件背叛策略,无条件背叛策略会占优无条件合作策略,无条件合作策略会占优互惠策略[2-4],这种互相占优关系会导致无条件合作策略抑制合作产生的这一奇怪现象.为了解决上述现象,本文在推荐合作激励模型[4]基础上引入了用户的理性背叛机制,最后理论和实验都证明了该机制在促进合作方面的有效性能.
2 相关工作
为了解决合作困境,研究者们进行了大量的激励机制研究.根据之前的文献,激励机制研究主要包含两方面的内容:金钱奖励机制和互惠机制.在金钱奖励机制中,合作者可以通过提供服务获取物质报酬,因其高效性和简单性,该机制已广泛应用于实际的协作系统中,例如:滴滴网约车平台,亚马逊在线工人平台,等等.在很多没有设置金钱奖励的协作系统里,互惠机制发挥了极其重要的作用.根据交互对象的特点,互惠机制可以分为:直接互惠和间接互惠.在直接互惠中,交互双方是保持不变的,其核心思想是“我帮助你,你帮助我”.一报还一报策略(Tit-for-Tat strategy,TFT)[5]是目前最知名的直接互惠策略,TFT策略使用者首先会采用合作行为,而在之后的交互中会采取对手上一轮的行为.为了增加TFT策略的鲁棒性,TF2T(Tit-for-Two-Tats)[6]策略和GTFT(Generous TFT)[7]策略随后也被提了出来.在Nowak的文章[8]中,赢留输改(Win-Stay Lose-Shift,WSLS)策略被提了出来,该策略使用者会保留一个收益期望值,如果当前收益不低于该期望值,则保留当前行为,否则,就更改当前行为,实验证明WSLS取得了比TFT更好的性能.在间接互惠中,交互双方是动态变化的,其核心思想是“我帮助别人,别人帮助我”.针对大规模P2P文件共享场景,Feldman提出了Mirror策略[9],当该策略使用者接收到一个服务请求后,他/她会计算该交互对手为别人提供服务的概率,然后以相同的概率为该交互对手提供服务.随后,Zhao等人[2]提出了Proportion策略,该策略使用者会计算交互对手提供的服务数量与其获得的服务数量的比例,并以该比例值作为自己与他人进行合作的概率,理论和实验证明,相比Mirror策略,Proportion策略能够更好地促进合作.Wang等人[3]研究了花费对Proportion策略性能的影响.Li等人[4]提出了基于推荐的合作激励策略(Recommendation Incentive Mechanism,RIM),该策略使用者在推荐机制的帮助下提高了自身与合作性节点交互的可能性,进而可以获得更高的收益,理论和实验证明,相比WSLS,Mirror和Proportion策略,RIM策略具有更好地促进合作的性能.在文献[4]的基础上,本文进一步引入了理性背叛机制,以解决互惠策略被无条件合作策略所抑制的这一问题,进而希望可以进一步促进合作的涌现.
另一方面,网络结构对参与者合作行为的影响目前也引起了广泛的关注,研究者们发现在网格网络[10],无标度网络[11],小世界网络[12]等结构化的网络中合作行为可以得到一定程度的促进.
3 模型构建
3.1 演化博弈
Maynard Smith在1982年提出了演化博弈理论模型[13],相比于传统的博弈论,它具有以下两个特性:
1)考虑了参与者的有限理性.由于在现实的复杂场景里,信息往往不能被完全感知,因此,参与者无法事先就做出最优的、最理性的策略决策,这就是参与者的有限理性假设.
2)动态的博弈结果展示.在传统的博弈论中,博弈结果往往是通过纳什均衡进行体现,然而这是一个静态的结果,有时人们对博弈结果的生成过程也很感兴趣.在演化博弈中,人们不仅可以获得博弈的最终结果,也可以了解结果的产生过程,从而对博弈模型有更多的了解.
基于以上两个特点,本文将使用演化博弈作为模型的基础框架来描述大规模协作系统里用户的交互过程.
3.2 推荐机制框架
基于用户交互的反馈信息,笔者之前文献[4]通过Eigentrust算法构建了一个合作性用户推荐系统,使用该系统的用户能够以一个更高的概率与高合作度用户进行交互,进而提高了获得服务的可能性.
3.3 策略集
假设系统中存在N个用户,每一个用户都会从策略集S中选择一个策略si作为自己与他人进行交互时的行为准则.在演化博弈中,使用了相同策略的参与者可以统称为一个种群(Population).
具体而言,本文模型考虑了下列三个纯策略.
无条件合作策略(ALLways Cooperate,ALLC):该策略使用者会一直为交互对手提供服务,模型中将该策略记为s1.
无条件背叛策略(ALLways Defect,ALLD):该策略使用者不会为其他用户提供服务,模型中将该策略记为s2.
推荐机制策略(Recommendation,R):该策略是一种有条件的合作策略,他/她会根据交互对象的类型决定自己的行为.当与ALLD策略用户进行交互时,他/她会选择拒绝为其提供服务.当与其他R策略用户进行交互时,他/她会选择提供服务.当与ALLC策略用户进行交互时,他/她会以f(f∈[0,1])的概率为其提供服务.当f=1时,就是笔者之前模型[4]里考虑的场景,此时会出现无条件合作策略抑制合作涌现的现象.本文考虑了推荐合作机制中的理性背叛场景,即f∈[0,1).特别地,当f=0时,R策略将不会给ALLC策略提供服务.模型中将该策略记为s3.
基于上述策略设定,本文引入一个3×3矩阵P=[pij]来描述策略间的交互行为:
其中元素pij表示策略si为策略sj提供服务的概率.
3.4 策略收益
收益是博弈模型中的一个重要元素,它直接说明了策略的好与坏.在计算策略收益前,先描述一下本文模型的交互场景:
1)一次机会.本文将协作系统建模成一个时间离散型模型,在一个时间步里,每一个用户平均意义上都有一次机会发起一个服务请求.
2)混合均匀的网络结构(Well-mixed topology).此时,每一个用户都是互相连接的,且能够以相同的概率进行交互.
3)一个请求者与一个提供者.本文假设每一个服务请求者会选择其他一个用户作为其服务提供者.比如,在百度云文件共享平台里,文件下载者会从一个云用户处获得完整的资源.单请求者多提供者模型可以参考其他文献[4,14].
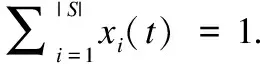
首先计算ALLC策略的期望收益.
当ALLC用户作为服务请求者时,在混合均匀网络结构假设下,他她会分别以x1,x2,x3的概率选择ALLC,ALLD,R用户作为其交互对象.由各个策略的性质可得,ALLC策略的期望收获可以表示为:
=α(x1+fx3)
(1)
其中α>0表示获得一个服务时用户的收益.
当ALLC用户作为服务提供者时,在一个时间步里,他/她会为ALLC和ALLD用户分别提供x1和x2次服务.基于交互历史,推荐系统[4]会将N1个ALLC用户和N3个R用户判定为合作性参与者,因为R用户会从合作性用户那里请求服务,所以平均意义上,每个ALLC服务提供者会以x3/(x1+x3)的次数为R用户提供服务.综上,ALLC策略的期望损失为:
(2)
其中β>0表示提供一次服务时用户的损失.
总而言之,t时刻ALLC策略的期望收益可以表示为:
(3)
同理,可以计算出t时刻ALLD和R策略的期望收益为:
(4)
(5)
其中γ>0表示用户采用R策略时需要为推荐系统支付的额外花费.
随后,通过公式(6),可以计算出t时刻系统的平均收益:
=(α-β)(x1+x3)-(α-β)(1-f)x1x3
(6)
在本文模型中,α,β和γ需要满足下面的关系:首先,α>β需要成立,即获得服务的收益要大于提供服务的损失,否则,合作将无法产生;其次,γ<α-β需要成立,否则,推荐花费过高将导致R策略无法在系统中存活.
3.5 演化过程
基于策略的收益,本文中引入了两种学习机制:全局平均学习(Global Mean Learning Mechanism,GMLM)[2-4]和当前最优学习(Current Best Learning Mechanism,CBLM)[2-4]来描述种群的演化过程.
3.5.1 GMLM学习机制
在交互完成后,用户会随机选择一个邻居,并与其进行收益的比较,如果自己的收益高于所选邻居的收益,则保持当前策略不变,反之,将自己的策略改变成邻居的策略,这就是GMLM学习机制.Börgers等人[15]证明在GMLM学习机制下,种群的演化过程可以使用复制动力学方程(Replicator equations)[2-4,12-14]进行表示,于是本文模型中,t时刻后ALLC,ALLD和R策略比例的变化可以描述为:
(7)
其中,λ表示策略的学习率,而且各个策略收益与平均收益的差可以具体由公式(8)~公式(10)表示:
(8)
(α-β)(1-f)x1x3
(9)
(1-f)x1(β+(α-β)x3)
(10)
定义1.在收益指导下,如果si策略能够最终被所有理性用户选择,即xi=1,那么可称si策略占优了整个系统.
推论1.在GMLM下,ALLC策略不能占优整个系统.
证明:这里使用反证法.假设ALLC策略能够占优整个系统,那么在x1→1,x2→0,x3→0时,下列3个不等式将会成立:
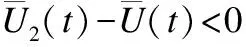
推论2.在GMLM下,ALLD策略不能占优整个系统.
证明:这里使用反证法.假设ALLD策略能够占优整个系统,那么在x1→0,x2→1,x3→0时,下列3个不等式将会成立:
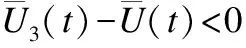
推论3.在GMLM下,当f≥1-γ/α时,R策略不能占优整个系统.
证明:这里使用反证法.假设当f≥1-γ/α时,R策略能够占优整个系统.那么在x1→0,x2→0,x3→1时,下列3个不等式将会成立:
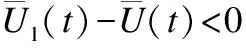
下面本文将讨论两种特殊的情况:f=1和f=0.
推论4.在GMLM下,当f=1时,那么ALLC,ALLD和R策略都不能占优整个系统.
证明:参见推论1、推论2和推论3.
推论5.在GMLM下,当f=0时,那么R策略会占优整个系统.
证明:此时可以计算ALLD策略与ALLC策略的收益差为:
所以,与ALLD策略相比,ALLC策略是一个严格的劣策略,根据博弈论中重复剔除劣策略方法,可将ALLC从策略集中删除,即令x1=0.然后,可以计算R策略与ALLD策略的收益差为:
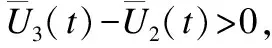
3.5.2 CBLM学习机制
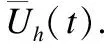
(11)
为了方便起见,在讨论模型在CBLM机制下的演化特性时,本文这里只考虑了f=0时的场景,此时有:
(12)
推论6.在CBLM下,ALLC策略不能占优整个系统.
证明:这里使用反证法.假设在CBLM下,ALLC策略能够占优系统,那么有:
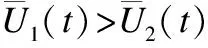
推论7.在CBLM下,ALLD策略不能占优整个系统.
证明:这里使用反证法.假设在CBLM下,ALLD策略能够占优系统,那么有:
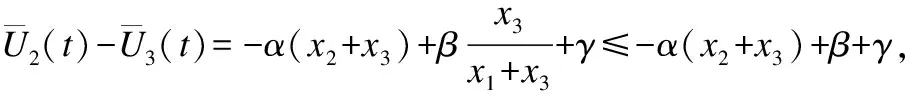
推论8.在CBLM下,当x2+x3>(β+γ)/α时,R策略能够占优整个系统.
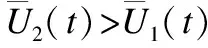
≥α(x2+x3)-β-γ
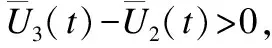
4 一些实际问题
4.1 非完美推荐
第3章在构建模型时只考虑了完美推荐机制场景,即推荐系统能够准确地分辨出用户的合作属性,进而R策略用户在每次交互中都能成功地获得服务.然而,由于数据获取时的噪声以及数据稀疏性等因素的影响,推荐系统往往不能做到100%的准确,因此,为了符合实际场景,还需要考虑在非完美推荐下本文模型的表现.
在非完美推荐下,系统可能会发生两种类型的错误:其一,是将背叛性用户误判成合作性用户;其二,是将合作性用户误判成背叛性用户.由于在现实场景里,背叛性用户会使用共谋、洗白等方法以提高自己被误判成合作性用户的概率,进而可以获得更多的服务,因此讨论理性背叛模型在第一种推荐错误下的性能是十分有必要的事情.
为了刻画第一类错误,本文引入参数δ∈[0,1]表示ALLD用户被误认为是合作性用户的概率.那么此时,R策略用户选取交互对象的规模就从N1+N3扩大为了N1+δN2+N3.
接下来,计算在第一类错误模型下各个策略的期望收益.首先是ALLC策略的期望收益.
当ALLC用户作为服务请求者时,他/她仍然能以100%和f的概率从ALLC和R交互对象中获得服务,故其期望收获保持不变,如公式(1)所示.当ALLC用户作为服务提供者时,其被R用户访问到的次数将变化为:
与之相对应地,ALLC策略的期望损失更新为:
综上,在第一类错误模型下,ALLC策略的期望收益为:
(13)
在计算ALLD策略期望收益时,此处考虑了最坏的情况,即ALLD策略会以δ的概率被误判为R策略,此时ALLD策略的期望收益可以表示为:
(14)
由于第一类错误的存在,以(x1+x3)/(x1+δx2+x3)的概率,R用户会获得服务,以fx1+δx2+x3/(x1+δx2+x3)的次数,R用户给其他用户提供服务,因此,R策略的期望收益可以表示为:
(15)
在非完美推荐场景下,模型的鲁棒性是一个值得关注的问题.具体而言,本文希望可以找到错误概率δ的临界值δc,当错误概率高于该临界值时,ALLD策略会占优整个系统.笔者之前的工作[4]讨论了f=1时,δc的近似解.本文将进一步讨论f=0时,δc的求解.
当f=0时,各个策略的期望收益如下所示:
ALLD策略占优整个系统的充要条件为:

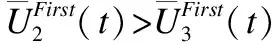
由于:
此时有:δ≥1-(β+γ)/α时ALLD策略能够占优整个系统.故δc=1-(β+γ)/α.注意该临界值是一个近似解,它表示了ALLD策略能够占优整个系统的充分条件.
4.2 ALLC与R策略的识别
如果每个用户都如实地公布自己所选择的策略,那么服务提供者就可以很清楚地根据对手类型,从而做出相应的反馈.然而,在更多的实际场景里,用户往往是不会公布自己的策略,此时,就需要根据用户间的交互历史来推断用户的类型.在之前的文献[4]里,笔者基于Eigentrust算法实现了用户合作度的评估,然而,这种方法不能直接用作ALLC和R策略的识别,因为他们的合作度可能都会很高.为了解决这一问题,本文提出了一种基于相似度的策略识别法.
首先引入Rij和Pij分别表示当前时间步t里用户i接收到的来自于用户j的服务请求数量和用户i为用户j提供服务的数量.那么用户i对用户j的合作度可以表示为:
(16)
基于此,可以构建出一个衡量用户间合作度关系的N×N维的矩阵C=[cij].由于ALLC是一个无条件合作者,他/她会为任何用户都提供服务,而R策略是不会为ALLD策略提供服务的,因此,可以通过衡量用户之间的行为相似度来帮助R策略使用者进行策略识别.
本文采用余弦相似度来计算任意两个用户i和j之间的行为相似度sim(i,j):
sim(i,j)=
(17)
其中,comn(i,j)表示共同向用户i和j发起过服务请求的用户集合.随后,本文引入一个阈值θ,当两个用户的行为相似度大于θ时,可认为二者采用了相同的策略,否则,可认为二者采用了不同的策略.综上,在本文提出的理性背叛模型中,R策略的行为可以由算法1表示.
算法1.基于相似度识别法的R策略行为决策
输入:
i:R策略的服务提供者
j:服务请求者
输出:
p:i对j提供服务的概率
1.基于文献[4],对j的合作度进行衡量
2.ifj是一个背叛性用户
3.p=0
4.else
5. 使用公式(17)计算i与j的相似度sim(i,j)
6.ifsim(i,j)>θ
7.p=1
8.else
9.p=f
10.returnp
5 实验及分析
本节将使用数值实验和仿真实验说明本文理性背叛模型的有效性,并对本文的理论分析进行了验证.
5.1 参数设置
实验中的参数设置如表1所示.在本文模型里,获得一个服务的收益α大于提供一次服务的损失β,为了和文献[2-4,14]保持一致,实验取α=7和β=1.R策略采取推荐服务时需要付出一定的花费γ,为了与笔者之前的文献[4]保持一致,实验取γ=0.7.在本文提出的理性背叛模型中,R策略与ALLC策略进行合作的概率为f,该值是一个从0到1的连续值.因为在现实场景里,只有很小部分的用户会及时去感知收益并进行策略更新,因此实验设置学习率λ=0.01.在仿真实验中,系统中的用户数量被设置为1000.在基于相似度的策略识别法里,实验将阈值θ分别设置为0.4,0.5,0.6和0.7.
表1 参数设置
Table 1 Parameters setting
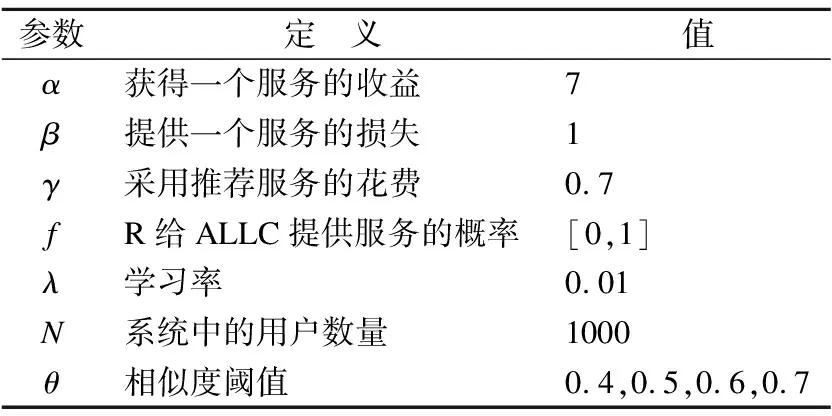
参数定 义值α获得一个服务的收益7β提供一个服务的损失1γ采用推荐服务的花费0.7fR给ALLC提供服务的概率[0,1]λ学习率0.01N系统中的用户数量1000θ相似度阈值0.4,0.5,0.6,0.7
5.2 f对模型的影响
首先进行数值实验研究在完美推荐场景下f对模型的影响.图1展示了GMLM学习机制下不同f值对应的策略演化结果.从图1(a)和图1(b)中可知,当f=0和f=0.8时,R策略都会占优整个系统,使ALLD策略从系统中消失.而且,相比f=0.8场景,f=0时R策略可以获得更好地收益,此时R策略可以更快地占优整个系统.如图1(c)和图1(d)所示,当f≥0.9时,ALLC,ALLD,R会互相占优并共存于系统之中.图1的实验结果很好地验证了本文3.5节中提出的推论1至推论5.当f取其他值时,策略演化结果是相似的,所以本文中就不进行展示了.
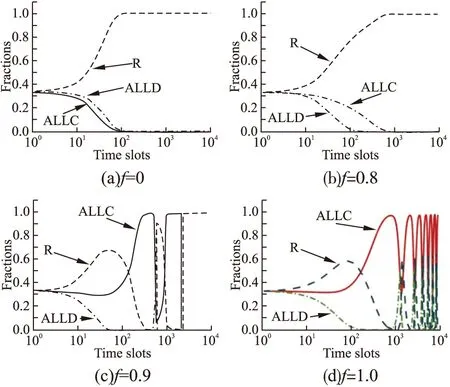
图1 GMLM学习机制下f对模型的影响[数值实验]Fig.1 Impact of f on the model with GMLM[numerical experiments]
图2展示了CBLM学习机制下不同f值对应的策略演化结果.与图1(a)和图1(b)相似,如图2(a)和图2(b)所示,在f=0和f=0.8设置下,R策略可以占优整个系统,并且f值越小,R策略占优系统所花费的时间就越少.图2(a)所展示的结果验证了本文3.5节中提出的推论6至推论8.与GMLM机制下的策略演化不同,如图2(c)和图2(d)所示,当f=0.9和f=1.0时,ALLC,ALLD,R不仅会共存于系统之中,而且它们的比例会趋向于收敛.在之前的文献[4]中,笔者已经详细地解释了f=1.0时系统会进行收敛的原因,此处就不赘述了.同样地,当f取其他值时,策略演化会呈现相似的结果,所以本文就不进行展示了.
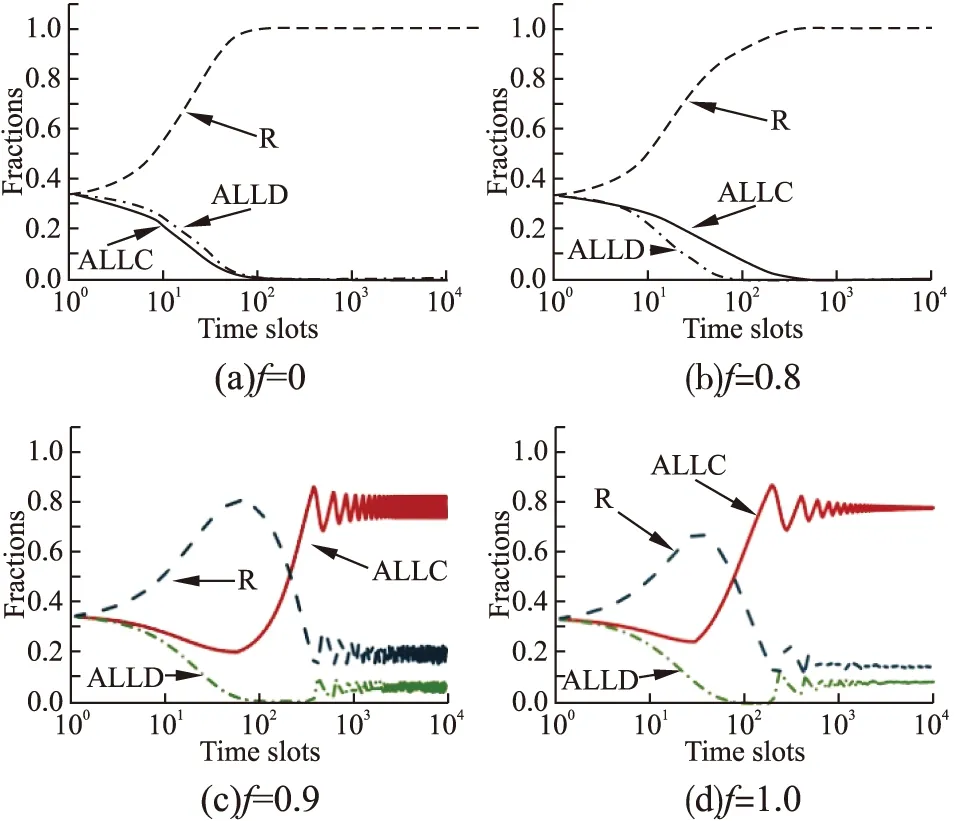
图2 CBLM学习机制下f对模型的影响[数值实验]Fig.2 Impact of f on the model with CBLM[numerical experiments]
基于图1和图2两个实验,可以发现:与不考虑理性背叛的模型(f=1.0)相比,考虑了理性背叛的模型(f<1)可以进一步促进合作的涌现,而且在本文参数设定下,当f<0.9时,无论在GMLM还是CBLM学习机制下,ALLD策略都会从系统中消失,从而合作行为获得了极大的激励.
为了验证数值实验的准确性,本文还进行了相应的基于智能体的仿真实验.图3和图4分别展示了用户数量N=1000时,在GMLM和CBLM学习机制下,系统中策略的演化过程.通过对比可知,仿真实验取得了与数值实验一致的结果.当N=5000,10000时,仿真实验也取得了相似的结果,本文就不进行展示了.
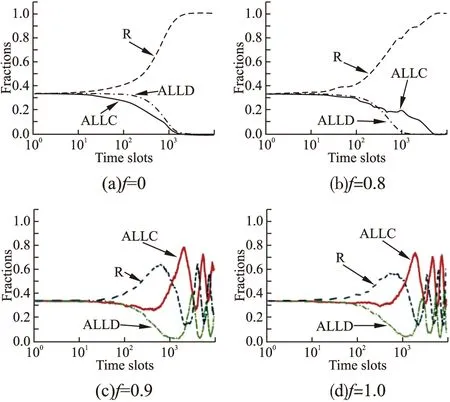
图3 GMLM学习机制下f对模型的影响[仿真实验]Fig.3 Impact of f on the model with GMLM[simulation experiments]
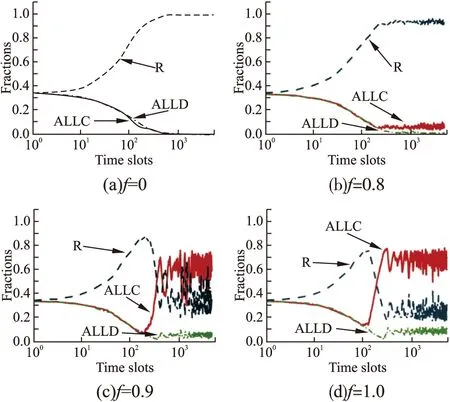
图4 CBLM学习机制下f对模型的影响[仿真实验]Fig.4 Impact of f on the model with CBLM[simulation experiments]
5.3 非完美推荐
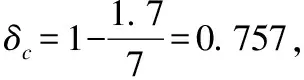
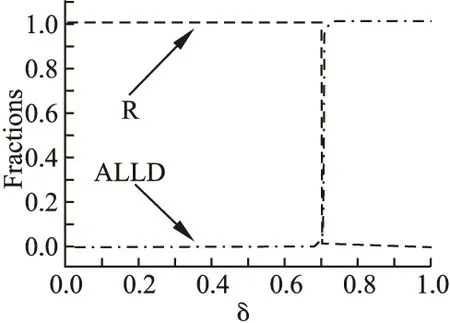
图5 GMLM机制下的非完美推荐模型Fig.5 Imperfect recommendation model with CBLM
5.4 相似度策略识别
这里,通过仿真实验研究了本文机制在部署相似度策略识别法后的策略演化过程.如图6(a)至图6(d)所示,实验分别设置相似度阈值θ=0.4,0.5,0.6和0.7.此处设定用户采用GMLM作为其策略学习机制.从图6(a)和图6(b)中可以发现,如果把阈值θ设置为一个较小的值时,R策略会大概率地将ALLC策略判断成R策略(此时等价于将f设置成了一个较大的值),并为他们提供服务,从而出现了如图1(c)和图1(d)所示的策略比例反复振荡的现象.图6(c)展示θ=0.6时的策略演化过程,在这种设定下,R策略可以较成功地进行策略识别,所以刚开始时R策略的比例可以大幅度地增长,随后,伴着ALLD策略的降低,R策略与ALLC策略的相似度会趋近于一致,因此R策略会大概率地将ALLC识别为R策略,进而促进了ALLC策略的增长.当ALLC策略增长到一定程度后,ALLD策略会得到激励.最终也会出现策略比例反复震荡的现象.从图6(d)中可以发现,如果把阈值θ设置为一个较大的值时,R策略会出现自相伤害的情况,进而不利于合作的产生.

图6 基于余弦相似度的策略识别Fig.6 Strategy recognition based on cosine similarity
综上,笔者认为θ取0.6是一个比较好的选择,在该设定下ALLD策略大部分时间内都可以被很好地抑制.在未来的工作里,笔者在计算相似度时将引入时间等因素,希望可以进一步提高策略识别的准确性.
5.5 对比实验
这里,通过对比实验将本文提出的具有理性背叛属性的推荐机制策略R与下列六种激励策略进行了性能比较:RIM[4],TFT[5],TF2T[6],WSLS[8],Mirror[9],Proportion[2].在比实验时,本文考虑了4500个用户,每个策略初始化时都拥有500个用户作为其策略种群.不失一般性,此处将R策略的合作参数f设置为0.如图7所示,随着系统的演化,R策略会逐渐战胜其他六种激励策略,并最终占优整个系统.在本文模型中,基于推荐机制,R策略能够以更高的概率获得服务,而且由于理性背叛机制的引入,R策略也避免了被ALLC策略所抑制,从而R策略可以在多策略对比实验中获得不错的表现.
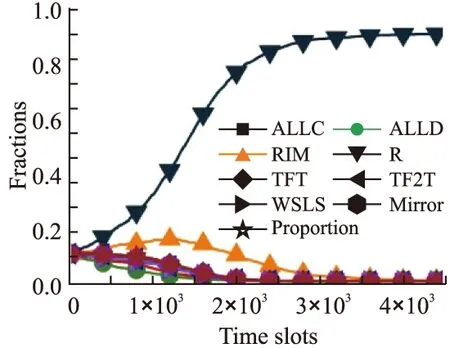
图7 多策略模型对比实验Fig.7 Performance comparison in a multi-strategies model
6 总结与展望
为了解决无条件合作策略对合作涌现的抑制现象,本文引入了理性背叛模型.在演化博弈框架下,针对两种不同的用户学习机制,本文研究了背叛概率对种群演化的影响,理论证明理性背叛机制的引入可以更好地促进合作的产生.接着,针对实际场景,本文首先研究了非完美推荐下模型的鲁棒性问题,然后,为了进行策略区分,进一步提出了基于相似度的策略识别法.数值实验和仿真实验都证明了理性背叛机制在合作促进方面的有效性能.在部署相似度策略识别法时,发现在动态演化的环境下准确地判断用户类型不是有一件容易的事情,因此,笔者将会继续对该问题进行研究.

