纯电动商用车异质队列的多目标控制*

王雪彤，罗禹贡，江发潮，于 杰

（1.中国农业大学工学院车辆工程系，北京 100083； 2.清华大学，汽车安全与节能国家重点实验室，北京 100084）

前言

近年来随着物流业的不断发展，货运在我国市场体量庞大，占国家GDP的16%～17%，据统计，保有量占7.96%的载货车引发的交通事故占事故总起数20.9%，致死率达到31.21%［1］。商用车的增加带来了一系列道路安全、燃油经济性和环境问题。

车辆队列的研究可追溯至20世纪80年代美国加州PATH项目，首次提出了车辆“队列化”的概念［2－3］。队列的研究主要基于车辆的跟车性能控制，体现在速度跟踪和距离跟踪。国内外学者多基于ACC技术开展队列的研究，验证了该技术在队列燃油经济性上较好的表现［4－5］。队列控制的节能问题是多目标控制的重点之一，现有车辆的节能控制主要有3种节能途径：（1）基于减小队列行驶车间距，以降低车辆行驶空气阻力，实现队列节能［6－7］；（2）基于获取道路信息和预测车队周围车辆信息，以减少队列行驶中不必要的大加速和大减速实现队列节能［8－10］；（3）基于制定合理的换挡策略，以减少车队行驶过程中频繁的换挡产生换挡间隙速度降低带来的额外能耗，实现车队节能［11］。以上研究均基于匀质队列（指车辆的整车质量、驱动性能和制动性能等均相同的队列），这一情况在实际生活中并不常见，即使相同车型车辆间也会因货箱的载质量不同导致整车质量差异，从而产生队列行驶的不稳定因素。随着队列在物流行业的应用不断增多和先进的控制理论的发展，队列行驶的非线性控制和多目标控制的问题日益凸显，控制系统不再只局限于单一跟车控制目标，而应将队列的跟车性能、节能、乘坐舒适性和稳定性多目标共同考虑。

为此，本文中以高速路纯电动异质商用车为研究对象，在分析异质队列结构和特性的基础上基于分布式非线性模型预测控制算法构造跟车稳定性、节能和舒适多目标协同的车辆队列控制器，同时在考虑道路信息的情况下优化队列行驶转矩以改善队列行驶的节能特性，并证明分布式非线性模型预测控制在算法上的控制稳定性；最后选取北京至天津高速路中的一段实际道路进行仿真，验证了系统的控制性能，结果表明，采用所提出的算法，队列的能耗可比PID定速巡航降低5.3%以上。

1 系统建模

1.1 电动车辆纵向动力学模型

由于车辆模型是非线性的，可通过反馈线性化的方式进行线性控制器的最优求解，但在具体的节能控制问题中空气阻力二次项和电机具有强非线性特性，当模型线性化后会导致整个车辆队列的节能效果不明显，且在异质车辆队列的控制中无法达到精确的控制效果，因此本文中采用非线性方程对车辆建模。

状态变量为车辆的位置、行驶速度和行驶转矩，即：xi（t）＝［Si（t），vi（t），Tq，i（t）］T，控制量为车辆转矩，即 ui（t）＝Tq，i（t），状态方程为·

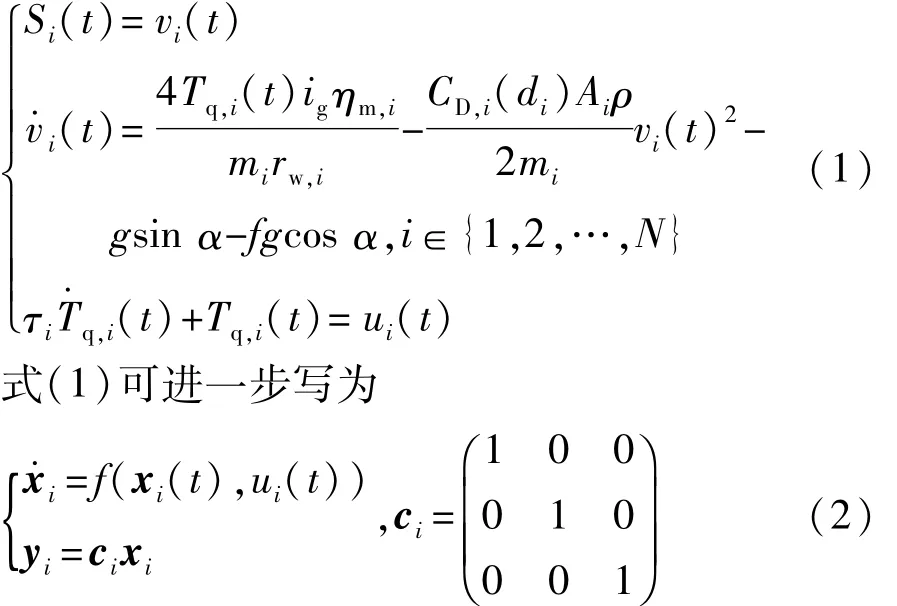
式中：i为车辆的编号；N为队列内的车辆数量；Si（t）和 vi（t）分别为车辆 i的位移和速度；Tq，i（t）为车辆实际驱动／制动力矩；ui（t）为期望驱动／制动转矩；mi为队列内车辆i的质量；Ai为车辆迎风面积；g为重力加速度；rw，i为车轮滚动半径；f为滚动阻力系数；τi为纵向动力系统的时滞系数；ηm，i为每辆车传动系统机械效率；CD，i（di）为队列内各车辆的空气阻力系数。

车间距是影响空气阻力的主要因素，因此队列内除领航车外引入以车间距变化的空气阻力系数：

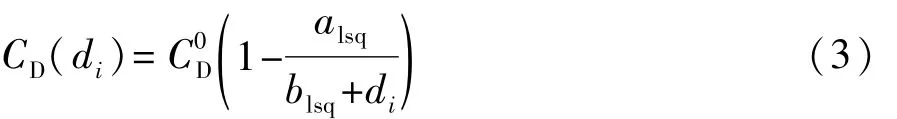
综上所述，为保证在计算机内计算的可行性对建立的动力学方程进行离散，其中Δt为每一步的时间步长。

1.2 电机能耗模型

考虑到电机能耗对车辆运行过程中节能效果的影响，电机功率的计算分为驱动和制动两部分，电机功率计算表示方式为

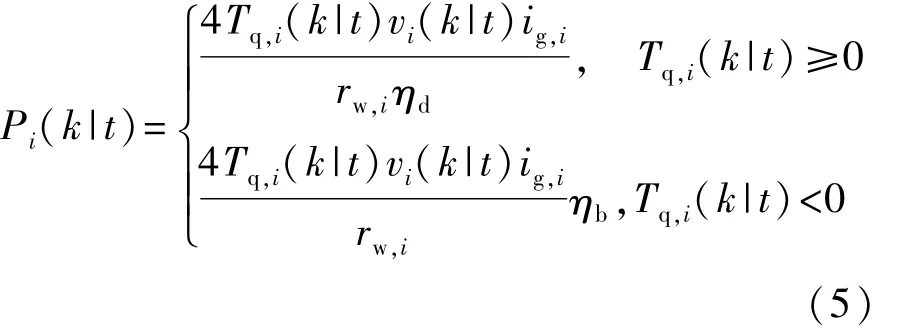
式中：ηd为电机驱动效率；ηb为电机制动效率。根据商用车的电机效率MAP拟合曲面将电机效率表示为转矩和转速的函数，如图1所示。

图1 电机效率MAP图

根据电机效率MAP图通过Matlab进行多项式曲面拟合，由此得到电机效率η关于转矩Tq和转速n的数学函数表达式。

当Tq≥0时，拟合函数为

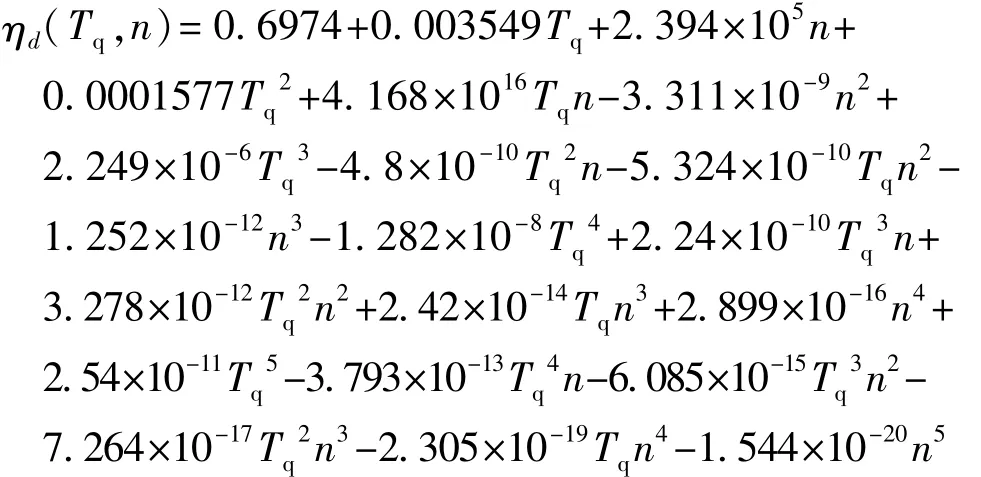
函数拟合精确度为99.5%。

当Tq＜0时，拟合函数为

2 分布式MPC控制系统设计

文献［13］中对队列几种通信拓扑结构的研究表明，PLF结构具有很好的队列稳定性潜力，即队列中领航车辆广播自身需要传送的信息，队列中的每辆车接收来自领航车辆和前车发送的信息。因此本文中基于PLF结构设计分布式模型预测控制器，采用分布式的计算结构能有效减小集中控制的压力，提高算法的运行速度。根据上述车辆动力学的建模，在异质车辆队列中的每个车辆上定义一个子预测优化问题，利用通信拓扑结构传递的信息进行优化求解，得到该车辆的控制输入。队列控制器分为车辆控制和节能控制两部分，车辆控制主要实现车辆跟车、稳定性和舒适性，节能控制则考虑电机效率和道路坡度的影响计算车辆的经济转矩，避免在坡道行驶时不必要的大加速和大减速产生额外能耗。

在解决非线性模型预测控制问题时的每一个预测时域内［t，t＋Np］定义 3种控制量序列：（1）预测控制量；（2）最优预测控制量（3）假设控制量其中预测控制量表示车辆的状态轨迹序列，用于参数化最优控制问题；最优控制量为通过滚动优化最优求解得到的控制序列；假设控制量为在通信拓扑结构内能与队列内其他车辆传递的控制序列，k＝0，1，2，…，Np。

2.1 领航车控制器

领航车辆控制器的设计目标是通过实时获取道路坡度信息，考虑道路坡度对自身转矩和速度的影响，从而计算由于环境变化影响的最经济车辆转矩，并将由该转矩计算得到的经济车速传递给跟随车辆。在检测道路坡度为0时，算法将维持车辆保证在既定经济车速行驶。因领航车在队列行驶过程中只起到获取道路坡度信息和计算队列经济车速的作用，故在设计该控制器时只须保证控制器的节能、稳定性和舒适特性，无须考虑跟车能力，且领航车在控制过程中只接收来自道路环境的信息，其控制框图如图2所示。

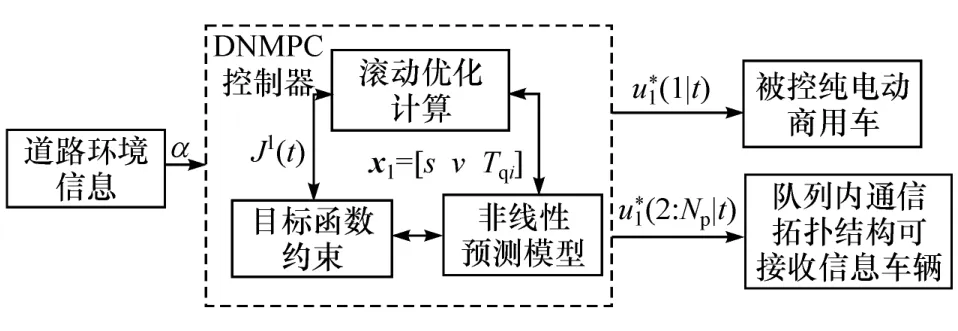
图2 领航车控制原理图

以下建立领航车辆的代价函数。

（1）经济性代价函数

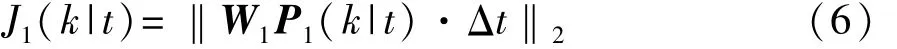
式中：W1为领航车的能耗权重系数矩阵；P1（k｜t）为领航车的电机功率。通过进行Np步的时间步长Δt迭代，计算Np步累加的最小能量消耗值达到预测时域内的最小电机能耗。

（2）舒适性代价函数

为保证行驶过程中的舒适性，转矩的变化率不能过大，因此最小化车辆计算的期望转矩与车辆在匀速稳态时转矩的差值，以减小控制器输出的期望转矩变化量。

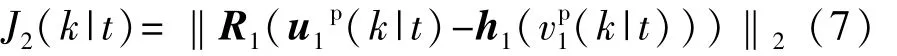
式中：R1为领航车的舒适性权重系数矩阵；h1（vp1（k｜t））为车辆在 vp1（k｜t）车速下匀速行驶的车辆转矩，如式（8）所示。

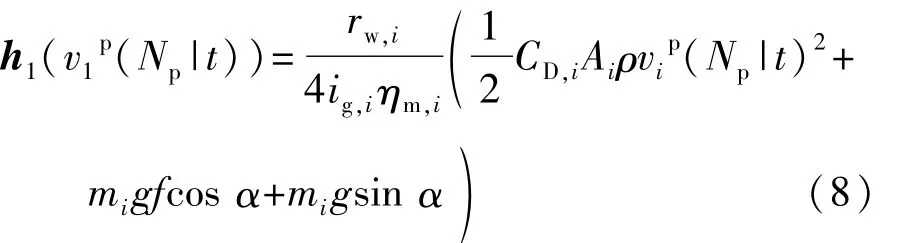
领航车控制器问题描述：

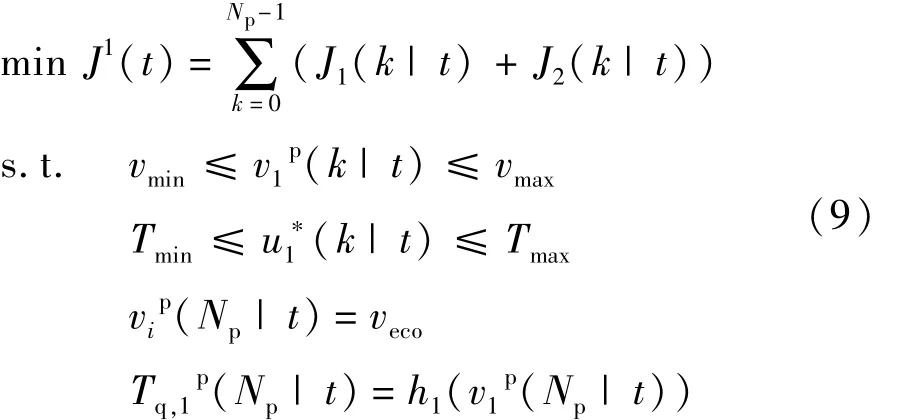
式中：vmin为高速路商用车行驶的最低车速60 km／h；vmax为高速路商用车行驶的最高车速100 km／h；Tmin为自车电机能够达到的最小转矩值；Tmax为自车电机达到的最大转矩值；veco为根据商用车辆行驶的经验设定的经济车速。为保证车辆的跟车稳定性能，对预测终端加以约束，使车辆在终端到达匀速稳态行驶，h1（v1p（Np｜t））表示车辆在 v1p（Np｜t）的车速下匀速行驶的转矩值，同式（8）相似。

2.2 跟随车辆控制器

车队跟随车辆的控制器设计目标是在保证跟随领航车和前车状态的同时，保证自车在检测到道路坡度时以最经济的车速行驶，建立约束保证整个队列的稳定，下述公式中i∈｛2，…，N｝，跟随车辆控制框图如图3所示。

以下建立跟随车辆代价函数。

（1）跟车误差代价函数

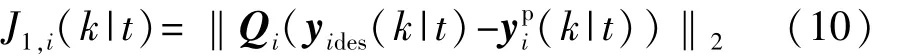
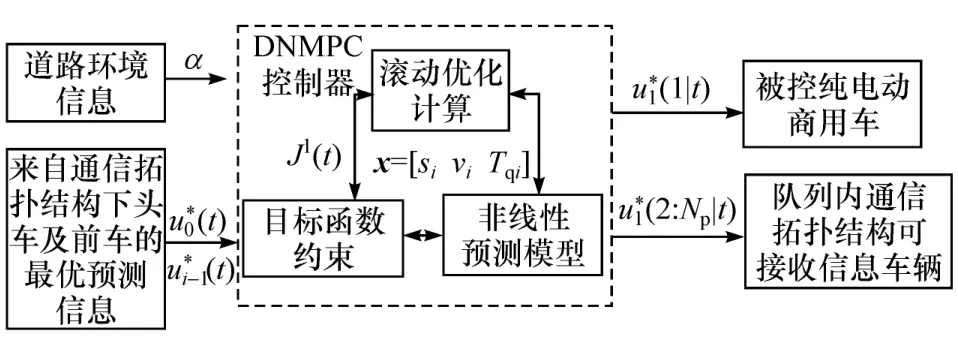
图3 跟随车控制原理图

式中Qi为自车与头车的误差系数矩阵。

建立自车与前车的跟车代价函数。同自车与领航车跟车代价函数相同，定义与前车的期望状态为

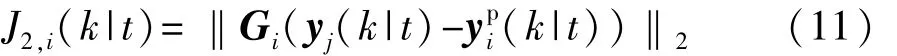
式中：Gi为自车与前车的误差权重系数矩阵；｜t）为前车当前时刻位置；k｜t）为前车当前时刻的速度。

（2）经济性代价函数

式中Wi为跟随车辆能耗权重系数矩阵。

（3）舒适性和稳定性代价函数

同领航车辆舒适性代价函数相似，跟随车辆舒适性和稳定性代价函数为

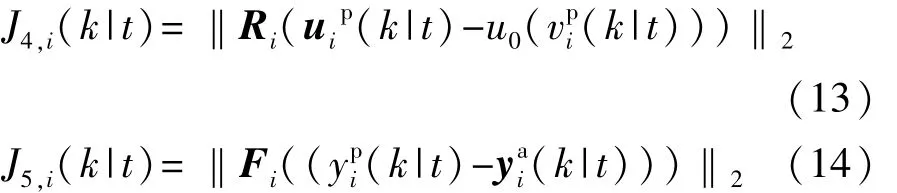
式中：Ri为跟随车辆舒适性权重系数矩阵；Fi为跟随车辆通信稳定性权重系数矩阵；ypi（k｜t）为车辆预测输出序列；yai（k｜t）为车辆通过通信拓扑结构向队列内其他车辆传输的序列。

跟随车控制器问题描述：

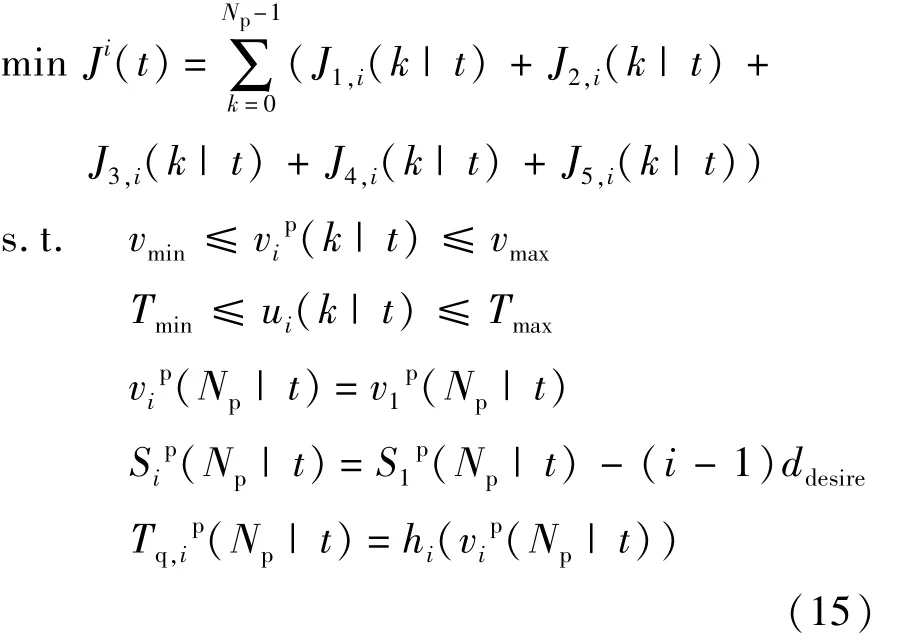
为保证跟随车辆控制器的稳定性设计终端约束，使车辆在每一个预测终端的速度与领航车速度相同，自车位置与领航车辆的期望位置一致，并保证在预测终端系统处于稳态即车辆转矩与匀速状态下转矩相同。在分布式模型预测控制过程中，每个优化时刻需要对所有车辆进行单点模型预测优化问题的求解，在单点模型预测控制中，车辆根据通信拓扑结构利用邻域车辆在上一个优化时刻得到的最优控制器输入作为当前时刻的预测输入，其传递的过程如图4所示。跟随车辆控制器设计与领航车控制器设计的不同之处在于跟随车辆需要在通信拓扑结构下保证跟随领航车和前车的状态，因此设计跟车误差代价函数，为保证跟随车辆的控制中不过多依赖于信息流，防止其带来的影响，在跟随车辆控制器中加入了预测状态量与接收到的假设状态量的误差代价函数J5，i，保证系统控制的稳定性。

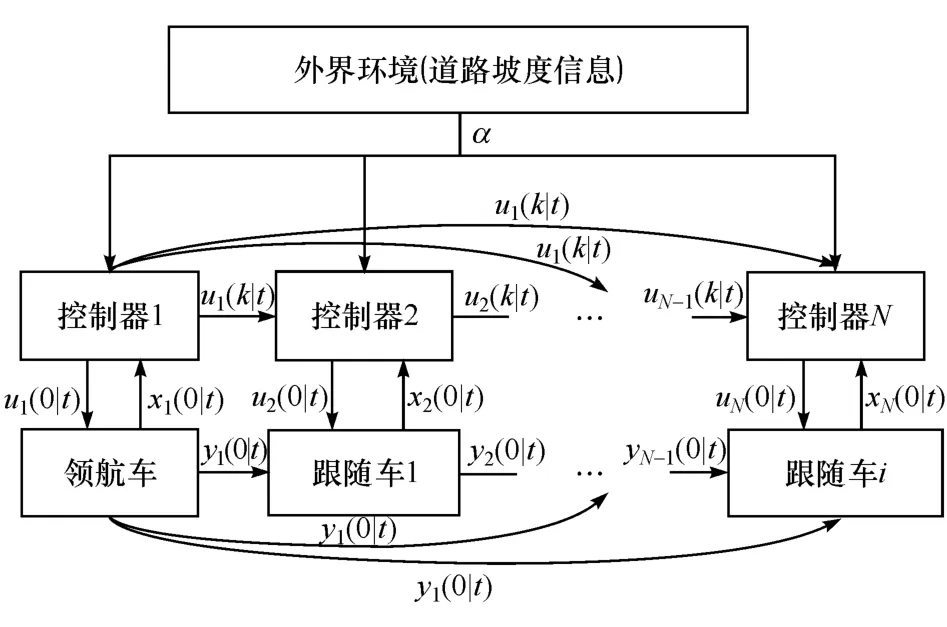
图4 控制量传递过程图

3 控制算法稳定性证明

假设x＝0是预测控制闭环系统的一个平衡点，在Lyapunov稳定性理论框架下给出稳定性的标准定义如下。

定义 1：如果对于任何 ε＞0，存在 δ（ε）＞0使得

‖x（0）‖＜δ（ε）⇒‖x（t）‖＜ε，∀t≥0 （16）

初始点x＝0附近是可控且稳定的。

定义2：如果闭环系统的平衡点x＝0是稳定的，并且可以选择δ使得

则闭环系统的平衡点x＝0是渐近稳定的。在Lyapunov稳定性的框架下以车辆队列总优化目标函数为候选函数，在任意时刻t，车辆队列总优化目标函数定义如下：

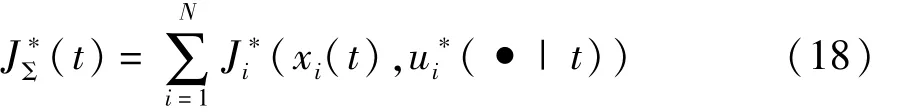
对于DMPC中的优化问题，当节点预测终端与期望状态一致后，全部控制节点代价函数单步迭代下降为

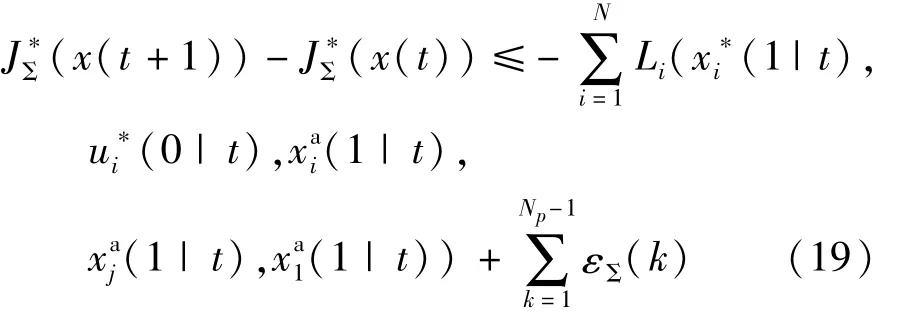
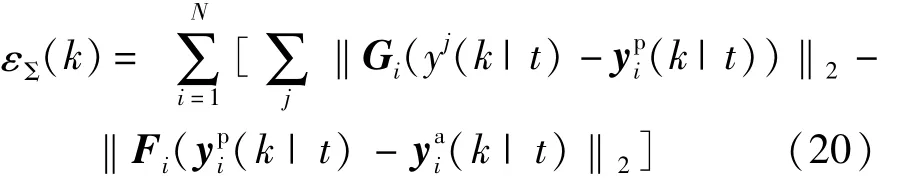
根据单车控制的单步迭代下降值，则有

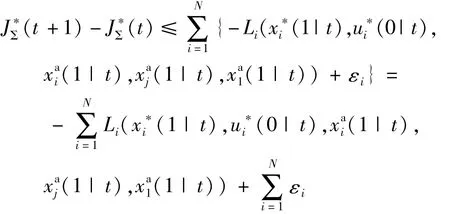
其中

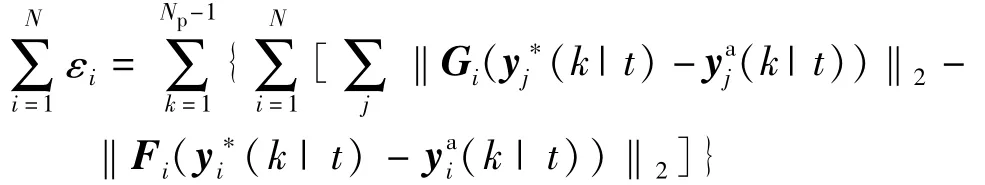
则根据上式可知：

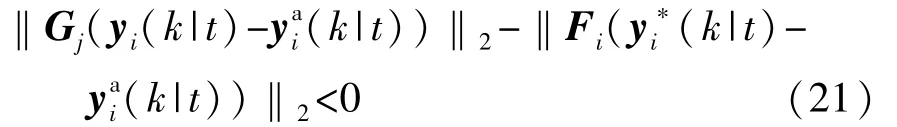
若要满足上式，Gi与Fi为人为设定权重值，因此满足 Gj≤Fi，i＝1，2，…，N，则可得到 J*Σ（x（t＋1））≤J*Σ（x（t）），根据 Lyapunov稳定性分析可知队列渐近稳定［14］。

4 系统性能仿真验证

为验证本文中异质队列研究方法的可行性，本文中基于Trucksim／Simulink搭建联合仿真平台，其中领航车权重系数如表1所示。

表1 领航车权重系数

跟随车辆的权重系数如表2所示。

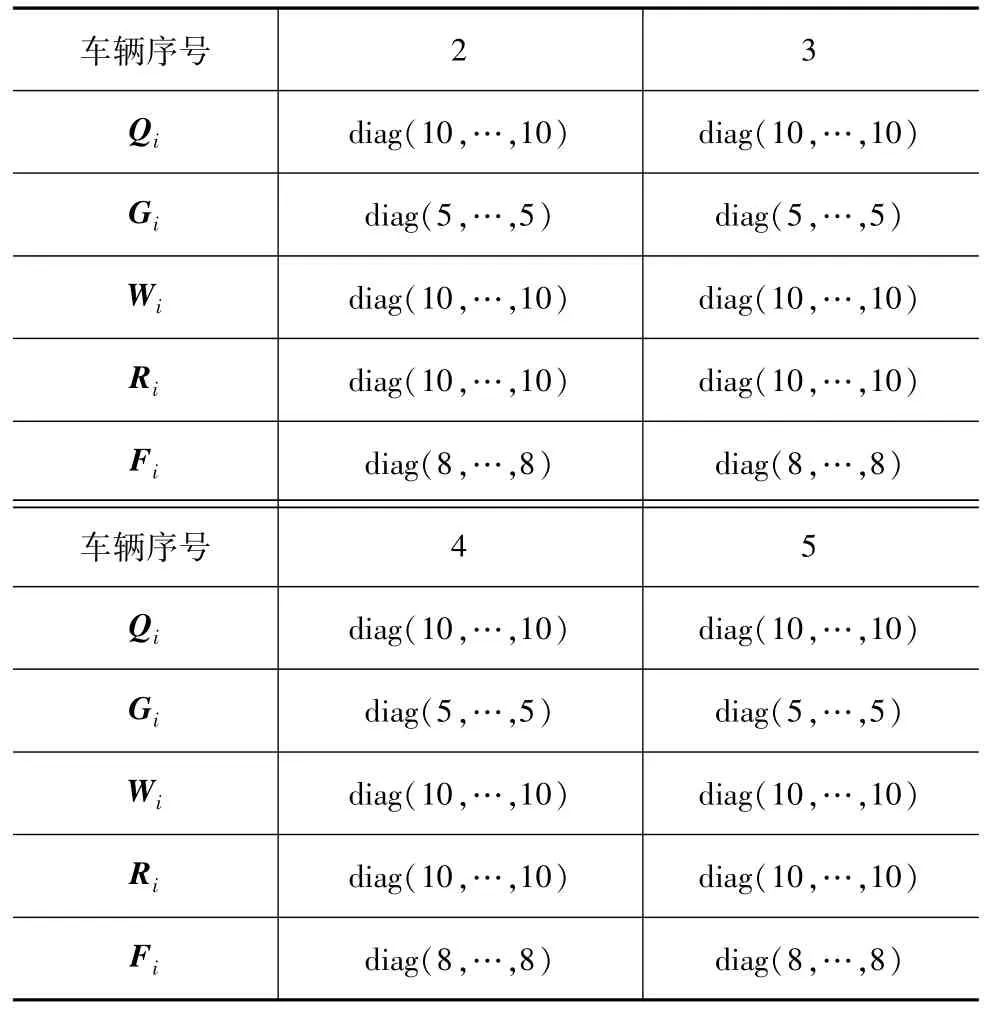
表2 跟随车辆权重系数

在高速工况运行过程中，异质车辆队列的车辆动力学参数如表3所示。

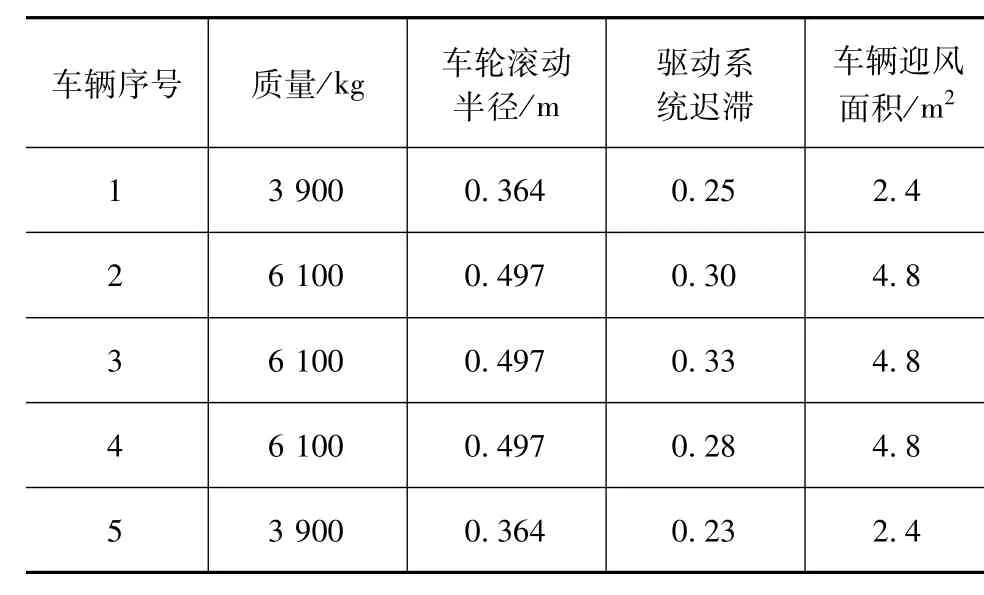
表3 异质队列车辆主要参数

4.1 平直道路工况队列仿真

模型在坡度为0的高速路直线行驶，队列内每辆车的初始速度为22 m／s。图5（a）为车辆队列速度跟随曲线，在车辆加速过程中由于为异质队列，其加速性能各有不同，但是依然能够保证整体跟车的一致性。图5（b）为车辆运行过程中前车与自车的速度误差，系统稳定后其误差小于0.02 m／s，在加速过程中有小范围内的波动但仍保持很好的稳定性。图5（c）为车辆运行过程中与前车的距离误差，在初始加速阶段由于车辆1和车辆2的质量有较大的差别，因此产生了一个较大的车间误差，但在短时间内控制器校正了这个误差，队列稳定后整体的最大距离误差小于0.05 m。图5（d）为车辆在坡度为0时与PID控制器定速巡航时能耗的对比，本文中提出算法相比于PID定速巡航的能耗节约6.96%，可以看出，在无道路坡度的工况下本文中所研究的控制器具有较好的经济性。表4中对比了与PID控制定速巡航的队列控制效果，可见本文中提出的算法具有更高的控制精度。

图5 异质无坡度仿真工况结果

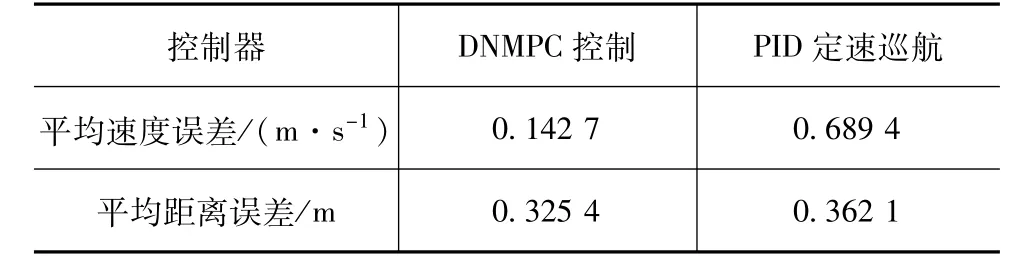
表4 控制器效果对比

4.2 上下坡工况队列仿真

假设高速路路面坡度如图6（a）所示，队列内车辆经过该坡度的时间各不同，因此各车在同一时间对应的坡度不同，队列期望经济车速为24.5 m／s；当车队行驶经过该坡度时，图6（b）为车辆的速度跟随曲线，当车辆遇到坡道时为保证经济性车辆会短暂加速以减少在遇到坡道时的急加速，并在下坡时不使用驱动依靠坡度提供的重力加速度维持车辆的速度，由图可知，队列内各车辆在经过坡道时依然可保证队列整体较好的控制性能，其中由于第1辆车与第2辆车和第4辆车与第5辆车之间存在较大的质量差，因此会造成控制误差扩大；图6（c）为车速误差曲线，由图可见，与前车的速度误差随着队列的延伸而减小，队列控制稳定后速度误差小于0.02 m／s；图6（d）为距离误差曲线，由图可见，车辆在经过坡道时由于每辆车需要预测坡度对自车控制器带来的经济性影响，因此会对车辆的距离误差产生影响，其突出表现在第1辆车与第2辆车和第3辆车和第4辆车之间，控制稳定后其距离误差小于0.05 m；图6（e）为能耗对比曲线，由图可见，与PID定速巡航控制相比，能耗降低了5.3%。本文中使用的控制器在坡道开始前先加速行驶保证其通过坡道，上坡完成后车辆依靠下坡时的重力完成行驶，在这个过程中车辆电机回收部分能量，最终达到整体运行节能的效果。表5对比了两种控制器的控制误差，可见本文中提出的方法具有更高的控制精度。

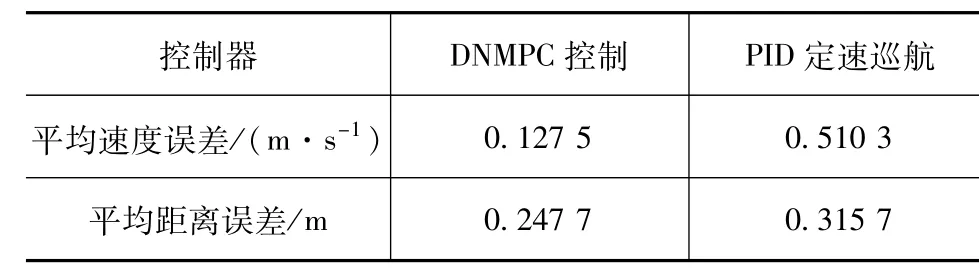
表5 控制器效果对比

4.3 实际道路数据队列仿真

为验证本文中提出算法在实际道路中的性能，选取北京到天津的一段实际高速道路，利用Google Map提取道路高程信息，输入仿真平台进行验证。北京至天津实际路段地图如图7（a）所示，其全程为122 km，从其中选取一段200 s的工况进行仿真。同样地针对队列的跟踪速度误差、距离误差以及与PID定速巡航控制的节能特性进行对比，仿真值如图7（b）～图7（e）所示。采用本文中算法可节约能耗5.99%。由表6可知，本文中设计的控制算法在实际道路工况中同样具有更优的控制效果。

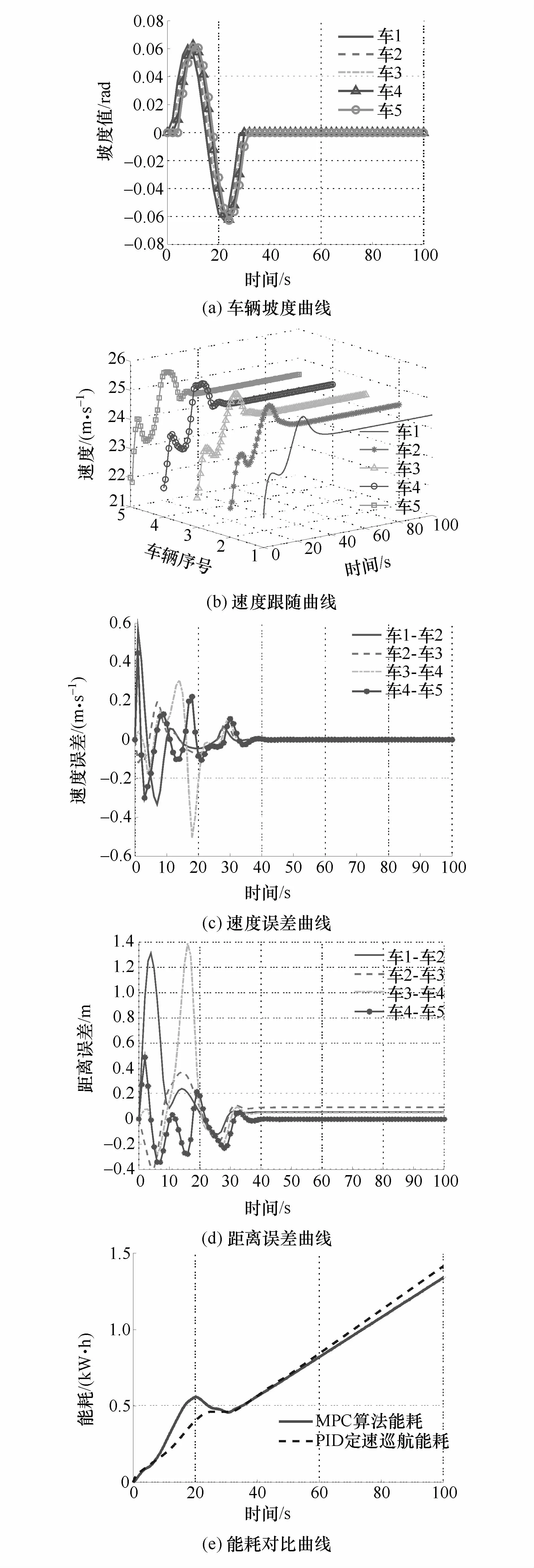
图6 异质有坡度仿真结果

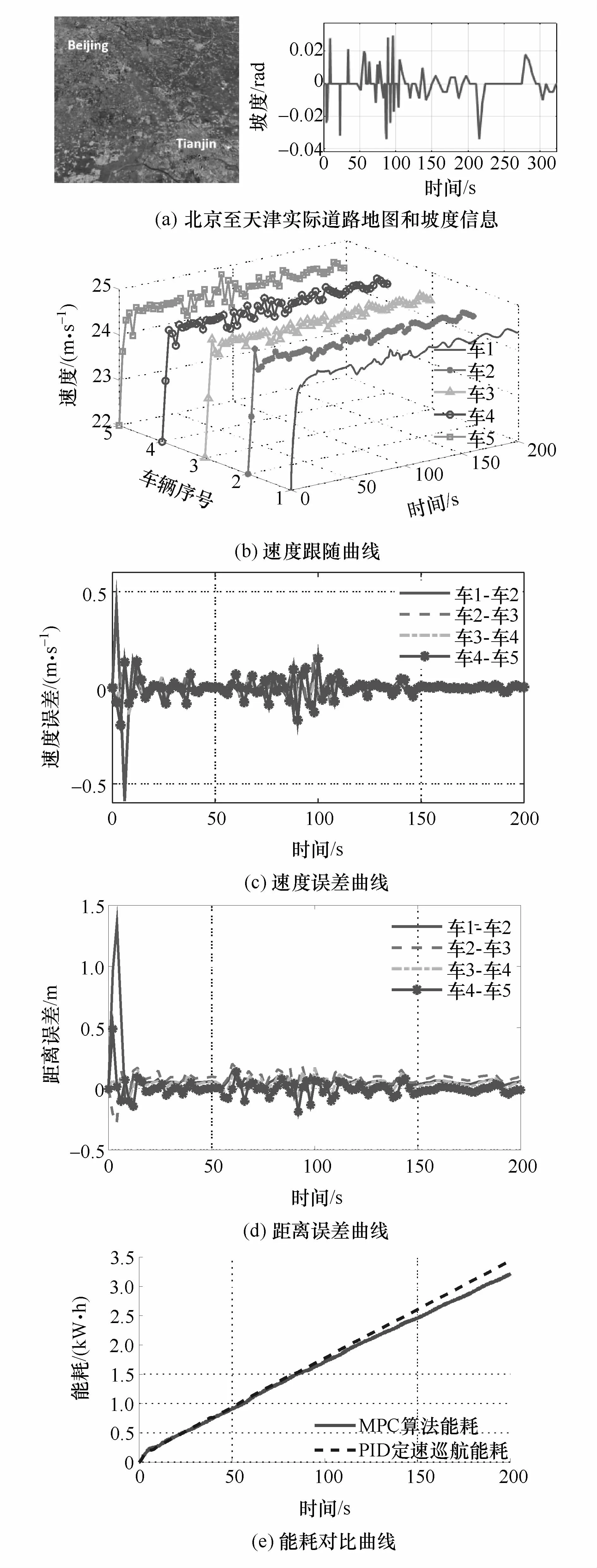
图7 实际道路坡度仿真结果

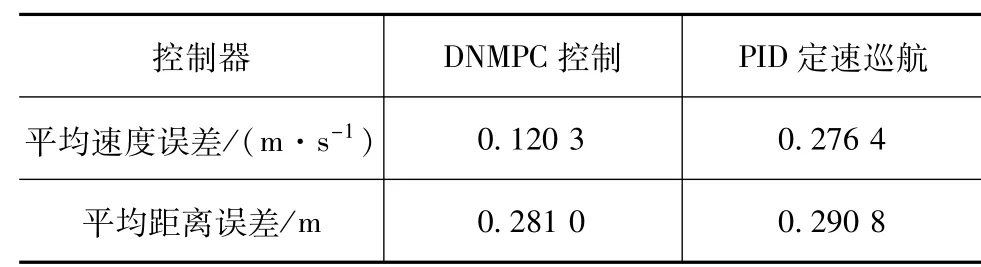
表6 控制器效果对比

5 结论

本文中以高速路异质纯电动商用车队列为对象，研究异质队列纵向的多目标控制，基于分布式非线性模型预测控制的方法，分别设计队列内领航车和跟随车的控制器，并在多种高速路工况下进行仿真验证，得出如下结论。

（1）本文中针对异质纯电动商用车队列的特征提出一种分布式非线性模型预测控制算法，通过建立车辆队列非线性模型，将队列车辆的质量参数、电机迟滞系数和其他车辆动力学参数加入滚动优化的过程中，保证异质车辆队列的稳定性行驶。

（2）基于分布式模型预测控制的方法设计的多目标控制器，在保证车辆队列整体跟车稳定性行驶和安全舒适的前提下根据道路情况优化车辆驱动转矩，实现车辆在高速路多种道路环境下行驶时的节能效果。