基于多维平行六面体模型的动力总成悬置系统固有特性分析*

吕 辉，杨 坤，尹 辉，上官文斌，于德介

（1.华南理工大学机械与汽车工程学院，广州 510640； 2.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082）

前言

受制造和装配误差、材料老化和复杂工况等因素影响，汽车结构系统不可避免地存在各种不确定性因素［1－2］。不确定性广泛存在于汽车动力总成悬置系统（powertrain mounting system，PMS）中，在实际工程应用中，对PMS的固有特性进行不确定性分析具有十分重要的意义。

近年来，基于不确定性分析技术的PMS固有特性研究受到了越来越多的关注。当系统参数信息充足时，可基于随机模型对PMS的固有特性进行设计研究。例如，张武等［3］、时培成等［4］将悬置的刚度视为随机变量，应用蒙特卡洛法对PMS的解耦率进行了稳健性优化。当系统参数信息匮乏时，可基于区间模型对PMS的固有特性进行分析研究。例如，吴杰等［5］、谢展等［6］将悬置刚度等关键参数处理为区间变量，基于区间分析算法对PMS的固有频率和解耦率进行稳健性优化设计。此外，吴杰和董志新［7］还对比分析了随机和区间模型在PMS稳健性设计中的应用研究。

上述研究工作均将PMS的不确定参数视为独立变量。然而，实际工程中汽车结构的系统参数之间往往存在一定相关性而非完全独立［8］。目前考虑参数相关性的不确定性分析模型主要有两种［9］：椭球凸模型（ellipsoidal convex model，ECM）和多维平行六面体模型（multidimensional parallelepiped model，MPM）。近年来，基于ECM的相关研究工作已经发展得比较成熟，而基于MPM的相关研究工作还处于初步探索阶段。此外，工程中的不确定参数往往不是全部相关的，例如某一部分参数间有相关性但它们与其他参数又互相独立。若出现多组各自相关的不确定参数组合，基于ECM的不确定性分析方法则需要建立多个椭球模型［10］，使得建模和计算过程复杂化，且不利于后续的优化设计。相较于ECM模型仅适用于参数具有相关性的情形，MPM模型可用于表达参数具有独立性，或者相关性，或者相关性和独立性共存的情形［11］。

对于汽车PMS模型，同一个悬置元件的三向刚度间往往存在一定的相关性［12］，但不同悬置点之间的刚度参数又相互独立，因而适合引入MPM处理悬置参数的不确定性和相关性。本文中针对汽车PMS不确定参数同时存在相关性和独立性的情形，基于MPM和蒙特卡洛法提出了一种PMS固有特性的不确定性分析方法，数值分析结果验证了方法的有效性和分析结果的合理性。

1 PMS固有特性计算

1.1 固有频率计算

建立汽车PMS模型时，一般将动力总成视为6自由度刚体，发动机通过N（N≥3）个悬置元件支撑在车架或车身上。图1为一动力总成横置、前轮驱动的动力总成悬置系统的6自由度模型［13］。

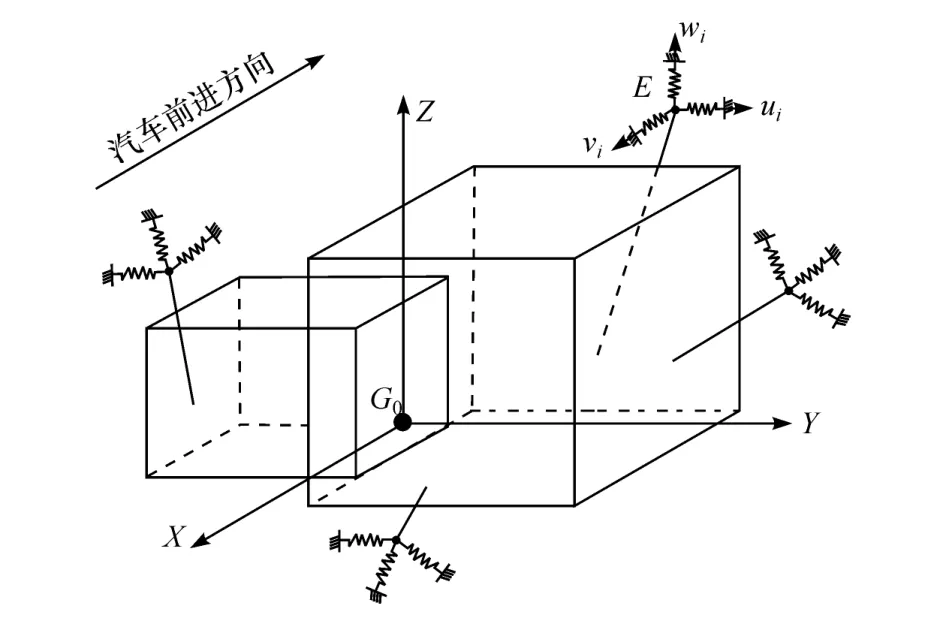
图1 汽车PMS的6自由度模型

动力总成坐标系G0－XYZ中，原点G0位于动力总成质心处，X轴方向与汽车前进方向相反，Y轴平行于发动机曲轴轴线方向并指向发动机前端，Z轴垂直指向上方。悬置元件简化为具有三向刚度的弹性元件，悬置的3个弹性主轴方向相互垂直，分别用ui、vi和 wi表示（i＝1，2，…，N，N为悬置个数），以 3个弹性主轴建立的坐标系E－uiviwi称为悬置的局部坐标系。

由下式可求得系统的固有频率和振型：

式中：K和M分别为悬置系统的质量矩阵和刚度矩阵。

求解式（1）和式（2），可得到系统的6阶固有频率 fj＝ωj／2π，j＝1，2，…，6，以及与之相对应的振型φj＝［φ1j，φ2j，…，φ6j］T。

1.2 解耦率计算

系统在作各阶主振动时，其能量分布在6个方向上，可以用矩阵形式表示系统的能量分布，即各个方向的振动能量所占的百分比。当系统以第j阶固有频率fj和振型φj振动时，第k个广义坐标所占的能量百分比［14］为

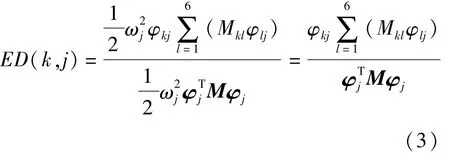
式中：φkj为 φj的第 k个分量。

第j阶模态对应的解耦率为

当Ej＝100%时，表示系统作第j阶振动时能量全部集中在某个广义坐标上，该阶振动完全解耦。

2 多维平行六面体模型分析

实际工程中可能存在这样的情形：不确定参数可分为若干组，组与组之间的参数相互独立，但每一组内部的参数又存在一定的相关性。对于此类复杂情形，可采用多维平行六面体模型（MPM）对参数的不确定性和相关性进行描述。文献［11］中给出了一种MPM的建立方法及其数学解析式。

假设系统存在s个有界不确定参数Y＝［Y1，Y2，…，Ys］T，不确定参数Yt的变化范围可用区间表示为

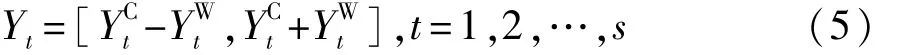
根据样本点数据，任意两个不确定参数Yt和Yl（t，l＝1，2，…，s且 t≠l）可构建一个四边形不确定域，如图2所示。若Yt和Yl相互独立，则两者所得的不确定域为图2中虚线所围的矩形域ΩS；若Yt和Yl之间存在相关性，则用图2中实线所围的平行四边形域Ω表示。

图2中，a表示半轴CA的长度，b表示半轴CB的长度。相关系数ρYtYl定义为

由式（6）可得－1≤ρYtYl≤1，且 ρYtYt＝ρYlYl＝1。a＝b时，ρYtYl＝0，此时 Yt和 Yl相互独立。

多维相关系数矩阵ρ表示为

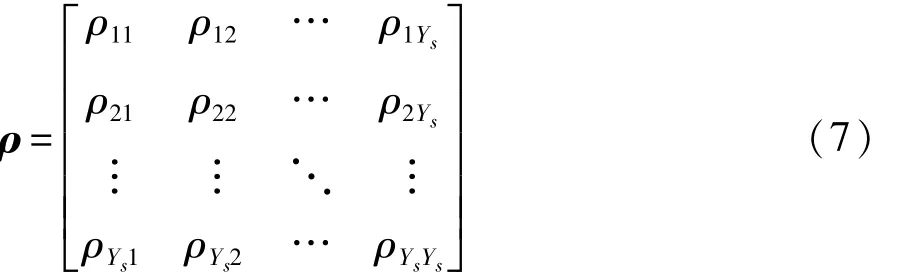
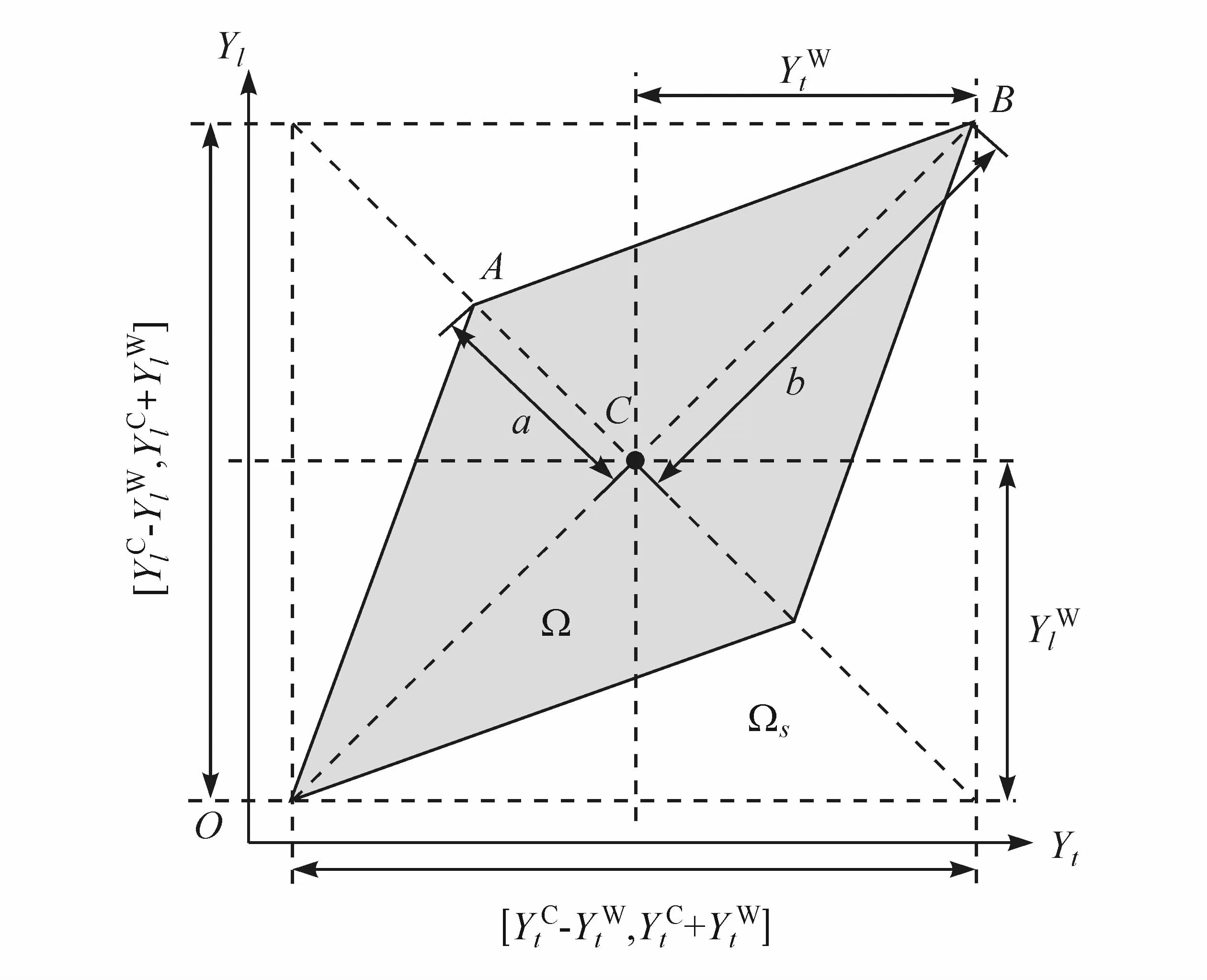
图2 二维不确定域

式中：ρ为 s×s矩阵；ρYtYt＝1（t＝1，2，…，s）。

s个不确定参数构成的多维平行六面体域的数学表达为

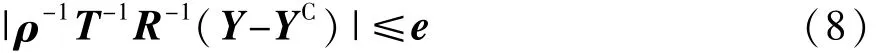
或

其中：

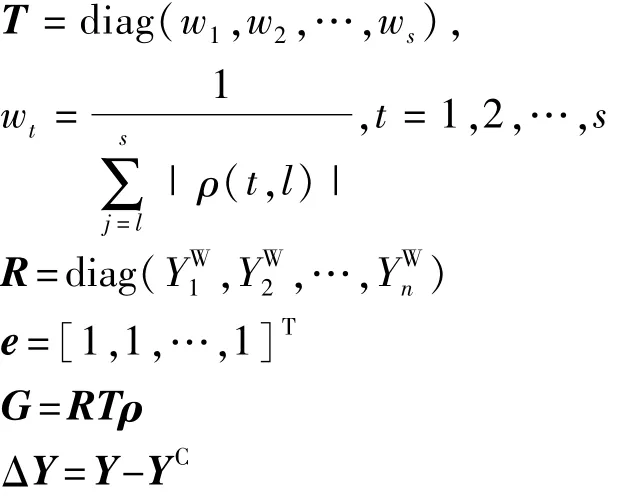
获得不确定参数样本数据后，通过以上方法可得到不确定参数的区间，并构建相关系数矩阵ρ，进而可建立MPM模型。在式（7）中，当矩阵ρ的所有元素取值为0时，对应的MPM即可用于描述所有参数相互独立的情形；当矩阵ρ的元素取值均不为0时，对应的MPM即可用于描述所有参数两两相关的情形；当矩阵ρ的部分元素取值为0，部分元素取值不为0时，对应的MPM即可用于描述参数相关性和独立性共存的情形。

3 参数相关性和独立性并存的PMS固有特性分析

对于PMS，同一个悬置元件的三向刚度参数往往存在一定的相关性，同时悬置与悬置间的刚度参数又相互独立。本文中将引入MPM和蒙特卡洛法处理悬置参数的不确定性和相关性。

分别以 fj（X）和 Ej（X）表示 PMS的固有频率和解耦率，j＝1，2，…，6，X为系统参数并用 MPM进行描述。蒙特卡洛法是应用最为广泛的一种不确定性分析技术。基于蒙特卡洛法和MPM求解参数相关性和独立性并存情形下的 fj（X）和 Ej（X），其主要步骤如下：

（1）对于悬置系统中的n个不确定性参数X＝［X1，…，Xt，…，Xn］T，t＝1，2，…，n，取任意两个参数Xt和 Xl（t，l＝1，2，…，n且 t≠l）的样本点，确定其区间的中点及半径，建立平行四边形不确定域，并计算出相关系数ρXtXl，对所有参数进行类似处理，由此得到相关系数矩阵 ρ，进而建立 MPM的解析式｜G－1ΔY｜≤e；

（2）将参数X视为独立变量，在其变化区间内进行蒙特卡洛仿真抽样，抽样结果记为 Xs＝［Xs，1，…，Xs，t，…，Xs，n］T；

（3）对 Xs进行筛选，将满足｜G－1ΔY｜≤e的样本数据记为 Xm＝［Xm，1，…，Xm，l，…，Xm，n］T；

（4）重复步骤（2）和（3）M1次，获得 M2组满足｜G－1ΔY｜≤e的样本数据，并将 M2组 Xm数据记为XM2＝｛Xm，1，Xm，2，…，Xm，M2｝；

（5）计算XM2中每一组样本数据对应的固有频率和解耦率，得到M2组固有频率和解耦率数据；

（6）分别找出系统6个方向对应的固有频率和解耦率的最大值和最小值，即为 fj（X）和 Ej（X）的上界和下界。

蒙特卡洛法的计算精度随仿真抽样次数M1的增加而提高，当抽样次数M1足够大时，能获得精确度很高的计算结果。

MPM能方便地分析多种情形下的PMS固有特性。一般地，不同悬置之间的刚度参数无相关性，对于具有N个悬置的PMS，悬置刚度参数的相关系数矩阵ρK可表示为

其中：

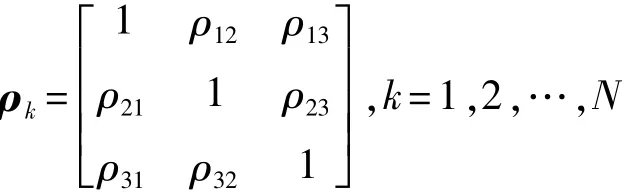
当所有参数相互独立时，ρK退化为一个n阶的单位矩阵。

4 算例分析

4.1 PMS模型

以某4点横置PMS为例［15］。动力总成质量为215 kg，表1给出了其转动惯量和惯性积数据，表2和表3分别给出了各悬置的初始静刚度和安装位置数据。

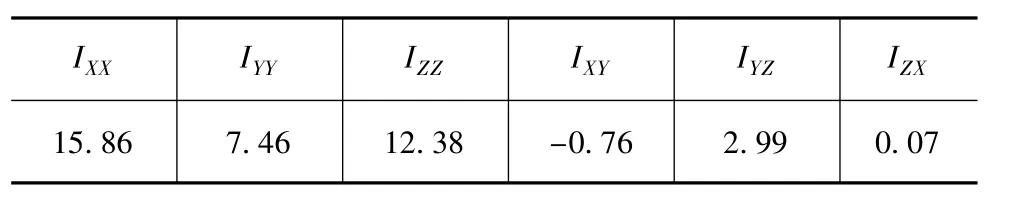
表1 动力总成的转动惯量和惯性积 kg·m2

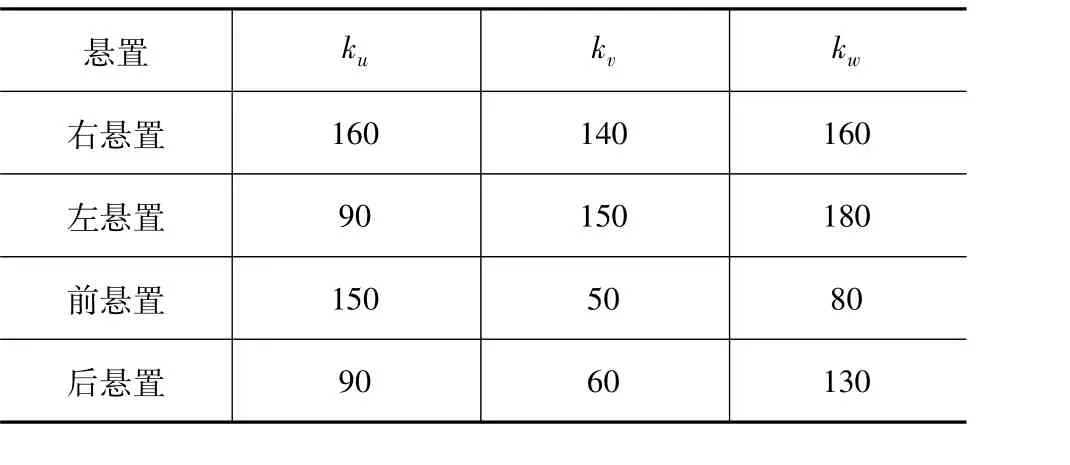
表2 悬置静刚度 N·mm－1

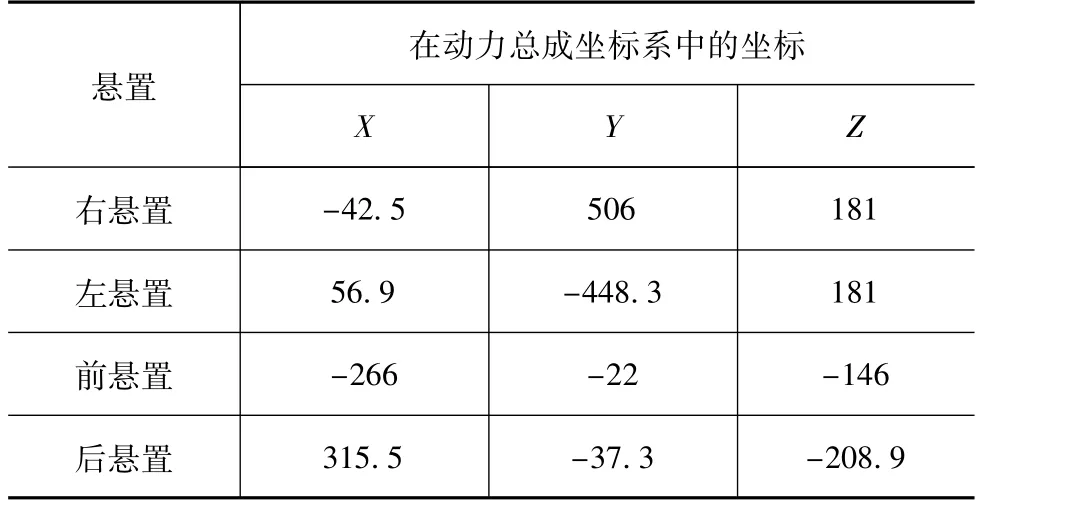
表3 悬置的安装位置 mm

4.2 基于MPM的频率及解耦率计算

相较于安装位置和角度参数，悬置的刚度参数更易实现调整和优化，且现有研究大多选择刚度作为研究参数。因此，本文中选择悬置刚度为研究参数进行分析。

工程中，当已获得悬置刚度的样本数据时，可通过刚度变量的区间和相关系数建立MPM。为便于分析，本文中直接给定不同情形下悬置刚度的MPM。

考虑同一悬置点三向刚度的相关性，且不同悬置点的刚度相互独立，对4个悬置点的刚度建立一个MPM。以表2中悬置的静刚度值作为设计变量的区间中点，设区间半径为静刚度的15%，即不确定度为±15%。令各悬置点的三向刚度的相关系数相同，均为ρ0，则刚度变量的相关系数矩阵ρK可表示为

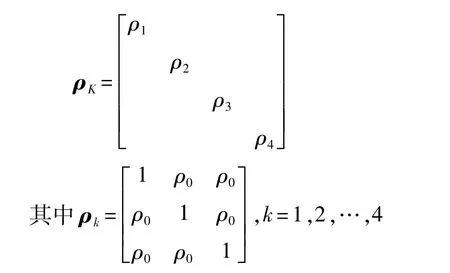
PMS6自由度分别为质心沿X、Y和Z轴的平动x、y和 z，以及绕 X、Y和 Z轴的转动 θx、θy和 θz。对于横置发动机，振动激励方向主要为z方向和θy方向［16］，因而在PMS设计时一般优先考虑这两个主要方向的固有特性配置。

分别研究悬置刚度的相关系数为0、0.1、0.2、0.3、0.4、0.5、0.7和 0.9等 8种不确定情形。根据第3节的计算方法可求解不同情形下系统的固有特性。表4和表5分别给出了各情形下系统z方向和θy方向的固有频率和解耦率的上下界数值。

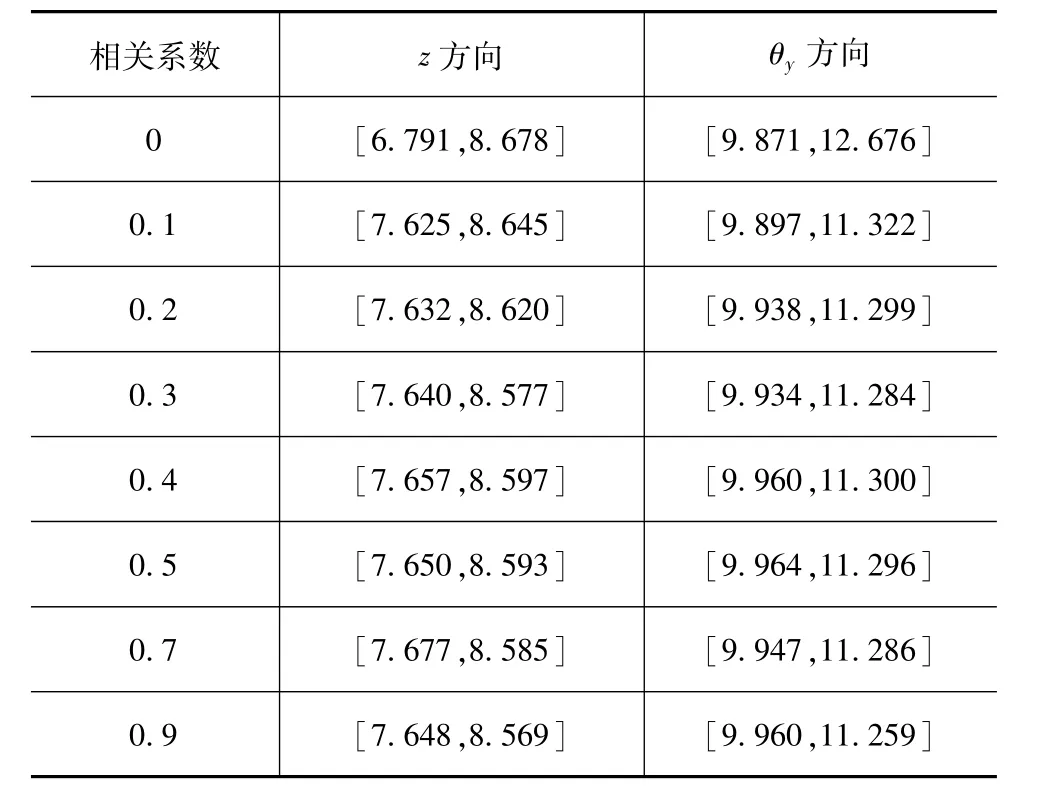
表4 PMS固有频率范围 Hz

为更直观地比较参数相关性大小对主要设计方向系统固有特性的影响，图3～图6分别绘出了不同相关系数下z方向和θy方向的频率和解耦率响应范围。

为分析考虑参数相关性后的结果对系统固有特性的影响，记偏差为纯区间情形（相关系数为0）计算得到的结果与其他不同相关系数情形计算出的结果之差的绝对值，以下通过偏差值进行数据分析。由表4、表5和图3～图6可得如下结果。

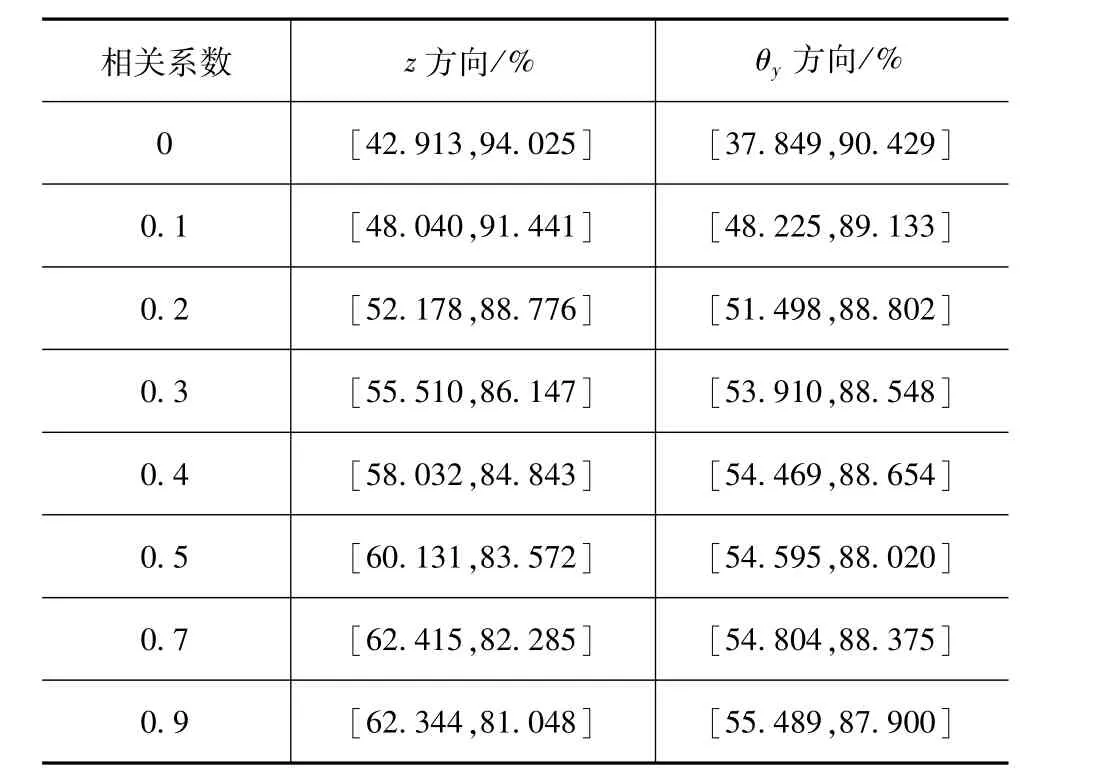
表5 PMS解耦率范围

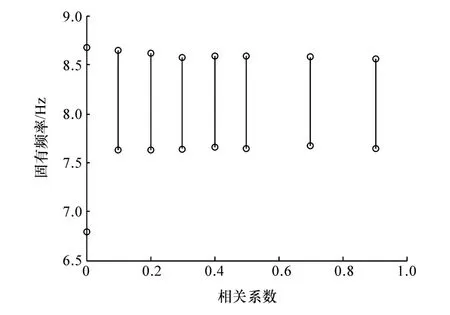
图3 不同相关系数下z方向的固有频率

图4 不同相关系数下θy方向的固有频率

（1）当相关系数为0，即各变量相互独立（退化为纯区间情形）时，系统频率及解耦率的变化范围最大。

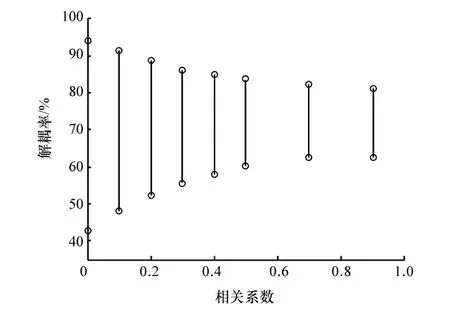
图5 不同相关系数下z方向的解耦率

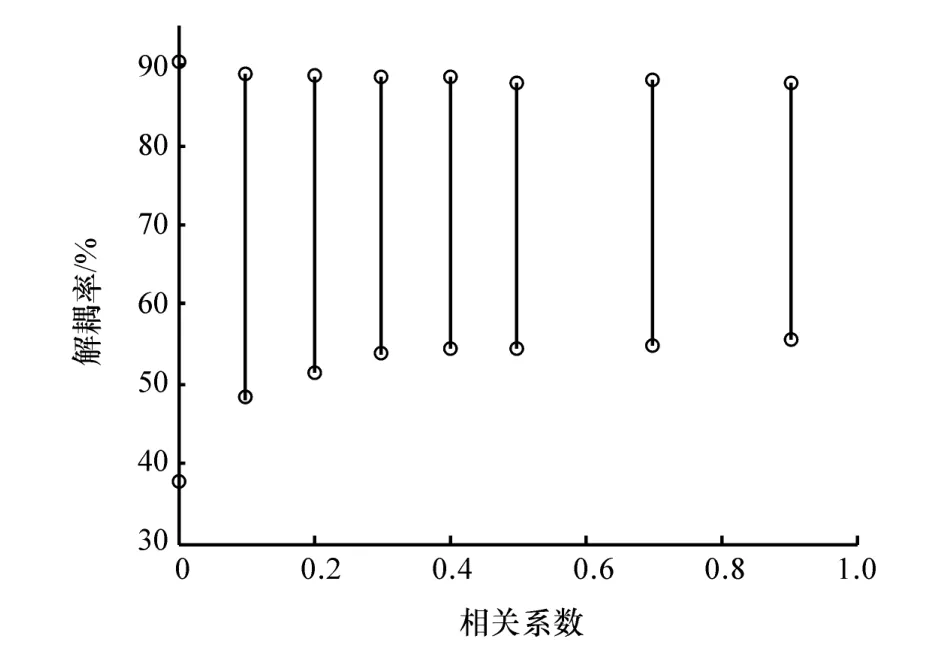
图6 不同相关系数下θy方向的解耦率

（2）对于固有频率，考虑参数相关性后，其变化范围缩窄，但相关系数的进一步增大对频率范围的影响不大。在z方向，参数相关性主要影响频率的下界，与无相关性的结果相比，当参数存在相关性时，下界频率的数值增大，出现了约0.9 Hz的偏差；在θy方向，参数相关性主要影响频率的上界，与无相关性的结果相比，存在约1.4 Hz的偏差。

（3）对于解耦率，考虑参数相关性后，其变化范围逐渐缩窄。在z方向，参数相关性同时影响解耦率的上下界，其偏差随相关系数增大而增加，与无相关性的结果相比，上界的偏差范围约为5%～13%，下界的偏差范围约为9%～19%；在θy方向，参数相关性主要影响解耦率的下界，与无相关性的结果相比，偏差范围约为13%～17%。

综合上述分析，对于本文中的研究模型，考虑其参数的相关性后，其固有频率和解耦率的响应区间均有不同程度的收缩，接近更合理的响应范围。对于PMS的主要设计方向，参数相关性主要影响z方向固有频率的下界和解耦率的上下界；而对于θy方向，参数相关性主要影响系统固有频率的上界和解耦率的下界。

4.3 各悬置参数相关性的影响分析

4个悬置的参数相关性对系统固有特性的影响效果应该是有所差异的。为甄别各个悬置参数相关性对系统特性的影响，下面研究仅某一悬置具有相关性时系统固有特性响应。研究过程中，依次任取某一悬置点并令其三向刚度具有相同的相关系数（本文中为0.5），且令其余悬置点的三向刚度相互独立（相关系数为0）。

图7～图10分别给出z和θy两个方向的固有频率和解耦率边界。横坐标表示具有参数相关性的悬置点名称，例如“无”表示4个悬置点的刚度相互独立，“左”表示仅左悬置点的刚度具有相关性而其他悬置点的刚度相互独立。

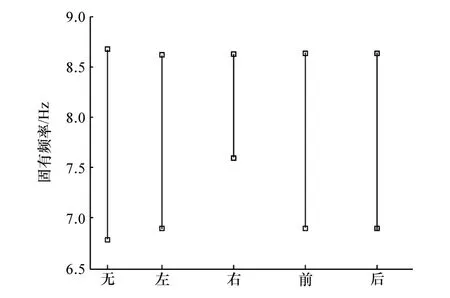
图7 仅某悬置参数相关时z方向的固有频率

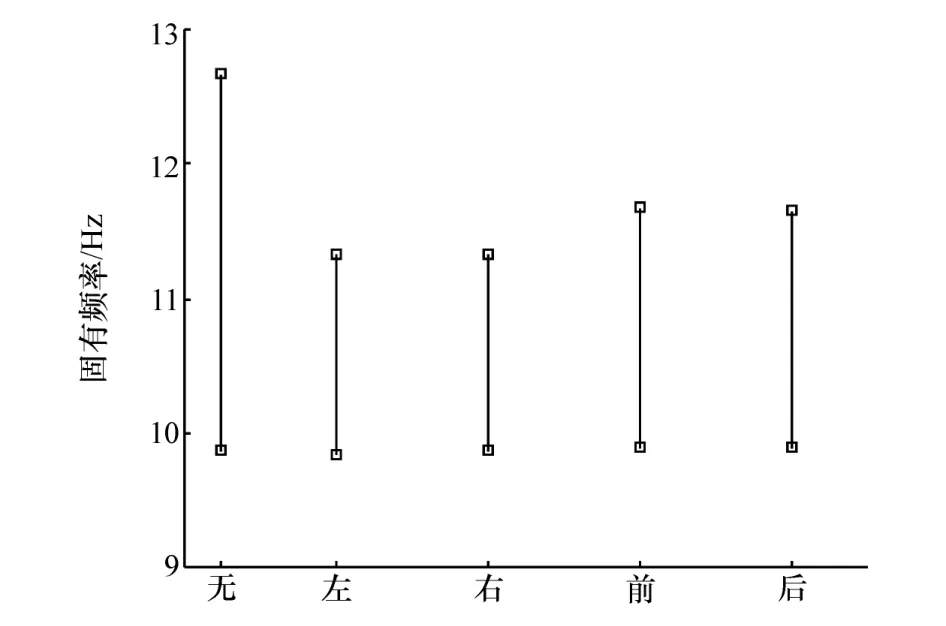
图8 仅某悬置参数相关时θy方向的固有频率

由图7可知，右悬置点的刚度相关性对z方向固有频率的影响最为明显，且主要影响频率的下界。其他3个悬置点的刚度相关性对z方向固有频率的影响较小。

由图8可知，左、右悬置点的刚度相关性对θy方向固有频率的影响比较突出，且主要影响频率的上界。而前、后悬置点的刚度相关性对θy方向固有频率的影响稍小，也主要影响频率的上界，且其影响效果相当。

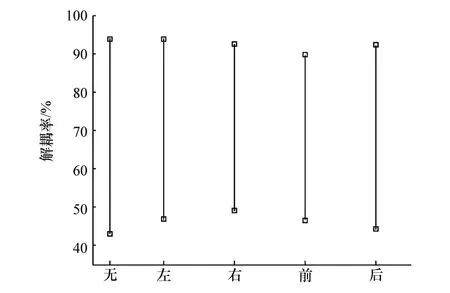
图9 仅某悬置参数相关时z方向的解耦率

图10 仅某悬置参数相关时θy方向的解耦率

由图9可知，4个悬置点的刚度相关性对z方向的解耦率均无明显影响，其中影响较大的是右悬置点的刚度相关性。

由图10可知，左悬置点的刚度相关性对θy方向解耦率的影响最大，且主要影响解耦率的下界。而其他3个悬置点的刚度相关性对θy方向解耦率的影响较小。

综合上述分析可知，对于本文中的研究模型，左右悬置点的刚度相关性对系统主要方向的固有特性影响比较明显，在设计和研究过程中应对该两点悬置的参数相关性进行重点关注。

5 结论

本文中提出了一种基于MPM和蒙特卡洛法的PMS固有频率和解耦率的分析方法，该方法能有效处理悬置不确定参数同时具有相关性和独立性的复杂情形。相关分析结果表明：（1）与未考虑参数相关性的区间方法相比，本文中的方法能获得更为合理的固有频率和解耦率区间边界；（2）对于本文中的研究模型，左右悬置点的刚度相关性对系统主要设计方向固有特性的影响比较明显，在设计和研究过程中应给予重点关注。