车辆端门碰撞振动产生声响的特性研究

唐斌斌， 李珂， 沈正建

（1.中车唐山机车车辆有限公司 服务事业部，河北 唐山063000，2.西安铁道技师学院 动车工程系, 西安710000）

0 引 言

为了满足车辆端门下滑道与导轨之间的滑动需求，必然会在滑道与导轨之间留有间隙，但在车辆运动过程中因外激励会导致产生碰撞振动，由于此类碰撞振动会持续产生“哒哒”的噪声，严重影响乘坐舒适性。此类碰撞振动问题自1931年Hartog等[1-2]开始研究库伦黏滞阻尼振子以来，碰撞振动系统成了研究的热点；罗冠炜等[3]研究了单自由度塑性碰撞振动系统，发现碰撞振子与约束面的擦边运动，造成庞加莱映射出现奇异性，同时系统经擦边运动进入复杂的长周期运动与混沌；张艳龙等[4]研究了含摩擦碰撞振动系统存在复杂的黏滞擦边碰撞振动、摩擦诱导黏滞混沌振动等；钱大帅等[5]利用谐波平衡法研究了干摩擦振子双黏着运动响应的级数形式解及对黏滑边界的分析；吕小红等[6]分析了相邻两次冲击之间，存在实擦边或虚擦边分岔和鞍结分岔等非光滑分岔，为解决实际工程中存在的碰撞振动问题提供理论基础。

本文将车辆端门滑道系统抽象简化出两种不同形式含间隙的碰撞振动系统，假定只在车辆纵向周期激励作用下，端门下滑道与导轨之间因间隙碰撞产生噪声。为了对比研究碰撞声响产生的原因及有效隔振消除振动声响，运用数值仿真方法对振动系统进行非线性动力学求解，分析端门滑道与导轨之间因间隙碰撞产生的噪声影响因素，进而为优化车辆端门结构消除因碰撞振动产生的噪声，对工程噪声的控制和解决提供理论基础。

1 滑道与导轨间隙碰-振系统模型

车辆端门滑道与导轨之间的装配示意图如图1所示，由于为了满足滑道在导轨上顺畅的滑动，滑道与导轨之间存在间隙无法避免。因此本文从滑道与导轨之间相对运动简化出两类碰撞振动系统。

1）含间隙的刚性碰撞振动系统力学模型如图2所示，将导轨两侧简化为约束面，略去约束面的厚度，滑道表示为质块M，其分别由刚度系数为K1和K2的线性弹簧及阻尼系数为C1、C2的线性阻尼器相连，刚性碰撞过程由碰撞恢复系数R确定，当质块M与约束面之间的位移差等于间隙D/2时，滑道与导轨发生碰撞，由于碰撞持续时间极短可略去不计。

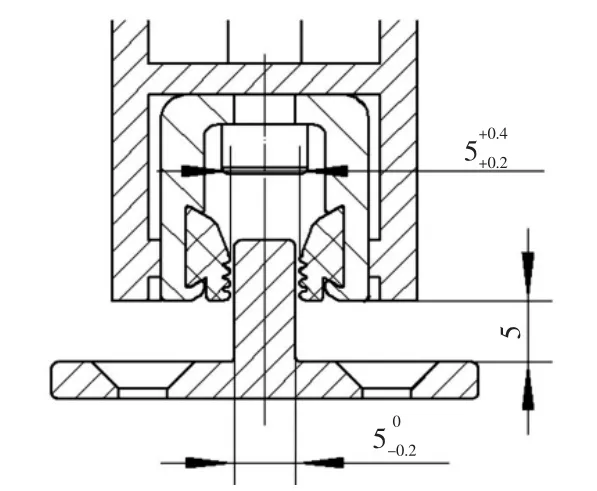
图1 端门滑道结构示意图

2）滑道与导轨之间采用弹性接触的隔振系统模型如图3所示，质块M分别由刚度系数为K1、K2、、K3和K4的线性弹簧及阻尼系数为C1、C2、C3和C4的线性阻尼器相连，滑道与导轨发生左右接触时，分别与线性弹簧K3和K4及线性阻尼器C3和C4起作用。车辆纵向振动传递到端门滑道的激励均表示为简谐激振力Psin（ΩT+τ）。

1.1 刚性碰撞振动系统模型

质块M的系统运动微分方程为

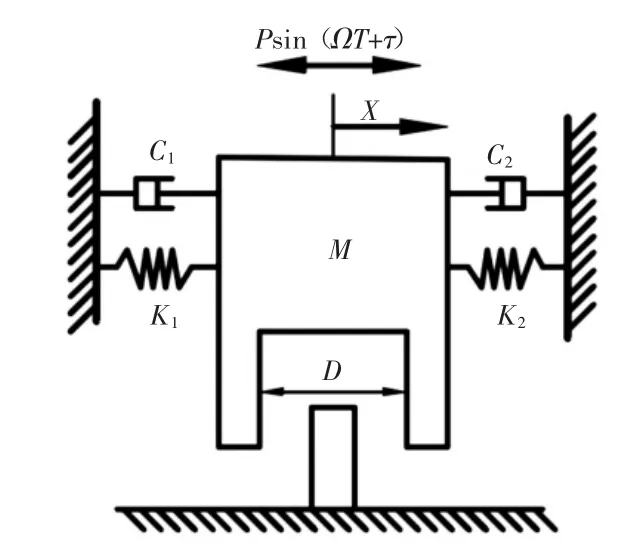
图2 刚性碰撞振动模型图

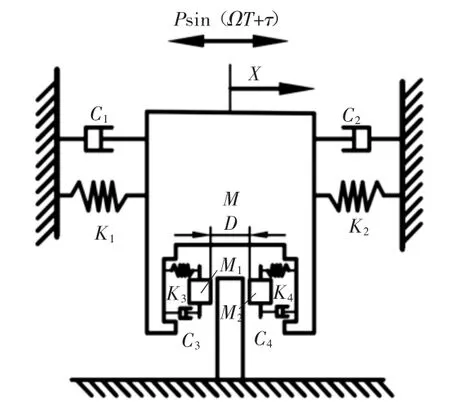
图3 弹性碰撞振动模型图

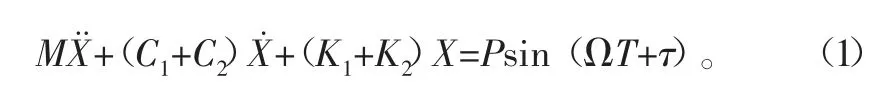
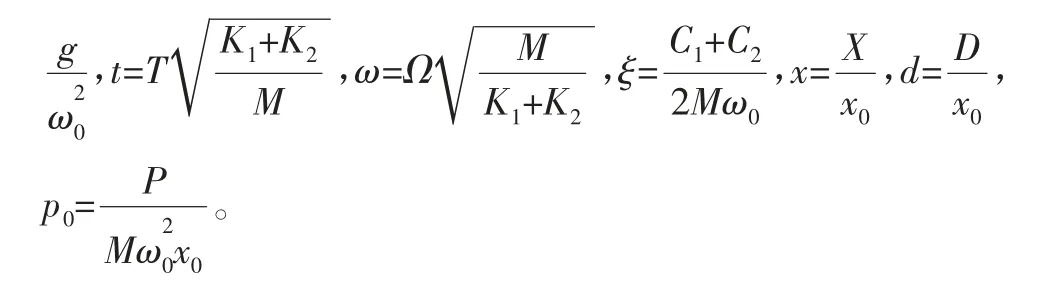
无量纲处理后系统运动微分方程为

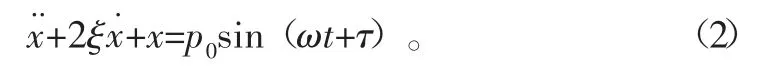
质块M与约束面的碰撞转换方程为

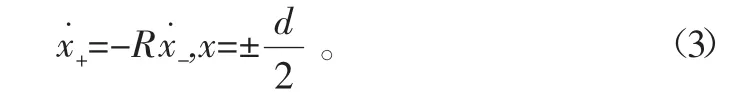
若质块M的运动位移x=±d/2时，质块与约束面发生碰撞，由于系统含碰撞构成非连续运动，质块在受到外力作用下连续与约束面发生刚性碰撞，不仅改变质块的运动轨迹，在碰撞过程中与约束面产生声响。根据质块的受力和碰撞速度变化情况，对质块与约束面之间间隙产生的碰-振系统进行数值仿真，分析刚性碰撞对系统振动及噪声的影响。

1.2 弹性碰撞振动系统模型

质块M与约束面发生弹性接触时受外激励作用的系统运动方程为

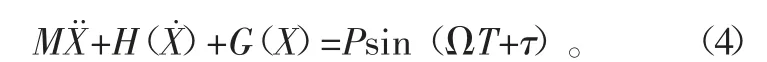
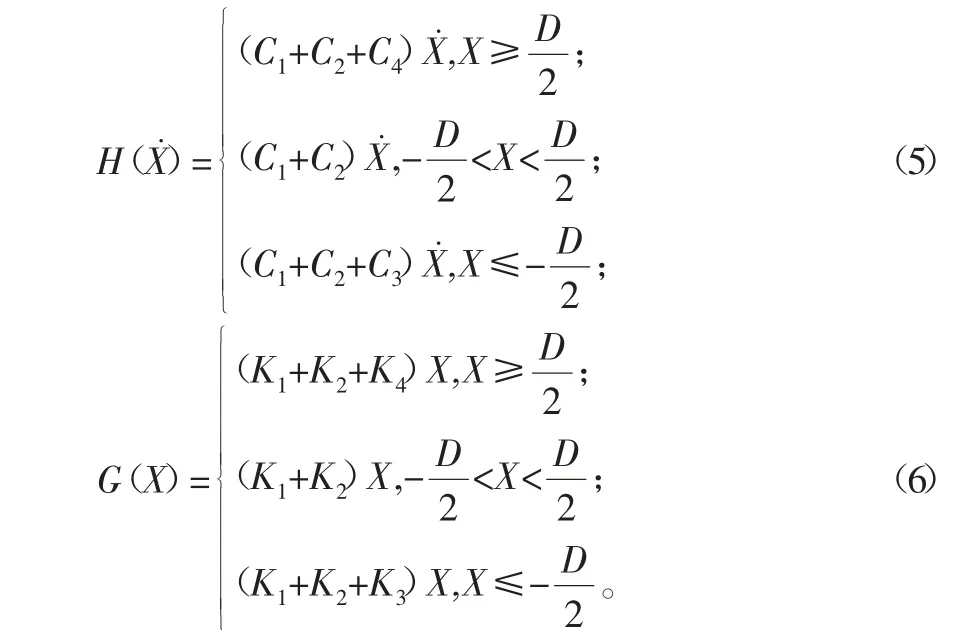
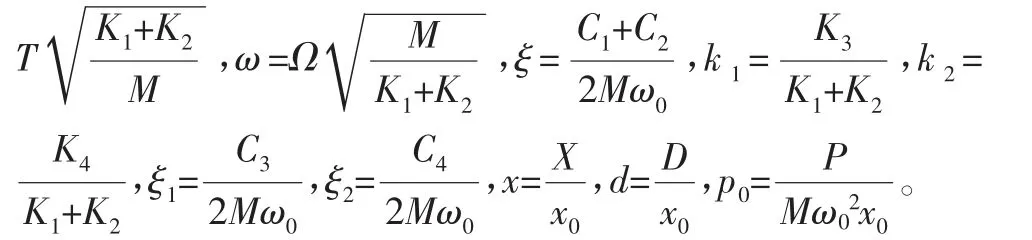
无量纲处理后弹性振动系统运动的方程为

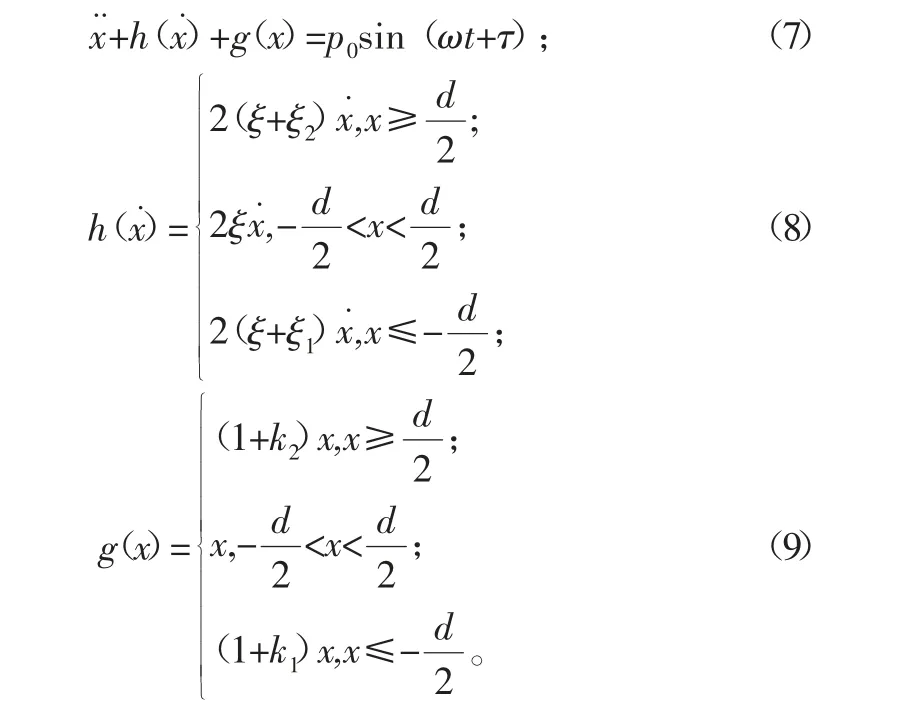
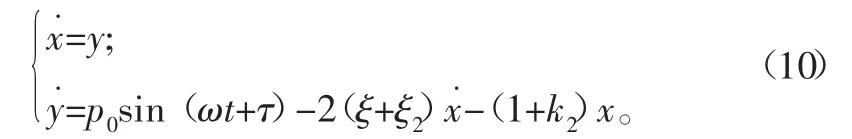
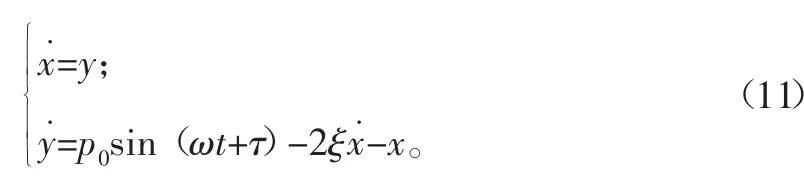
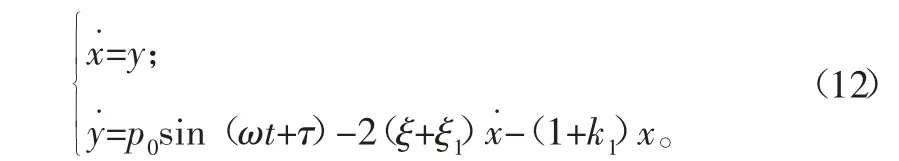
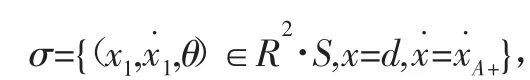
2 刚性碰撞对端门振动系统的影响

为了更好地阐述系统运动的规律及说明碰撞产生噪声的机理，选取系统参数：ξ=1.0,d=0.2,R=0.7,p0=2.0,设定初始值：x1=x˙1=0，以σ作为Poincaré截面，激振频率ω为分岔参数，端门系统随着激振频率的变化呈现出不同碰撞运动，系统全局分岔如图4所示。当激振频率ω在0.2～1.3范围内时系统运动呈现出1-N多周期运动，在此范围内，系统碰撞运动速度主要在“0”附近，表现出低速颤振碰撞，如在激振频率ω=0.5处的相图呈现了在一个周期力下质块与约束面发生了多次碰撞的运动现象，如图5（a）所示；当激振频率ω在1.8～2.1范围内时系统运动呈现出1-2周期运动，此时反映出在一个激励周期内滑道与导轨发生了两次碰撞；当激振频率在2.6～3.4范围内运动时呈现出混沌运动，此时反映出滑道与导轨之间碰撞出现混沌运动，碰撞振动最为激烈，如激振频率ω=3.0展示出的相图如图5（b）所示；当激振频率在3.5～6.4范围内运动时呈现出1-1周期运动，此时反映了系统在1个周期内滑道与导轨只碰撞一次，如激振频率ω=4.5展示的相图如图5（c）所示；当激振频率在6.5～8.0范围内运动时出现1-0周期运动，如激振频率ω=7.0展示的相图如图5（d）所示，此时反映了系统在1个周期内运动，滑道与导轨之间没有发生相互碰撞，无碰撞就不会产生碰撞声响，此为系统运动最优解。

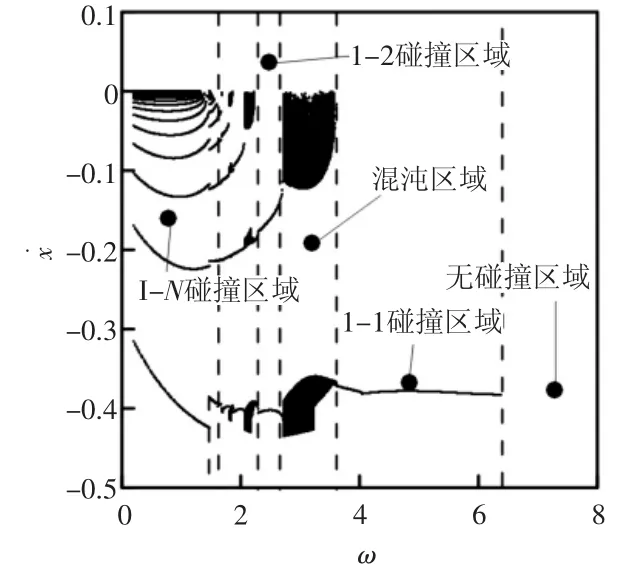
图4 刚性碰撞系统全局分岔图

3 弹性碰撞对端门振动系统的影响

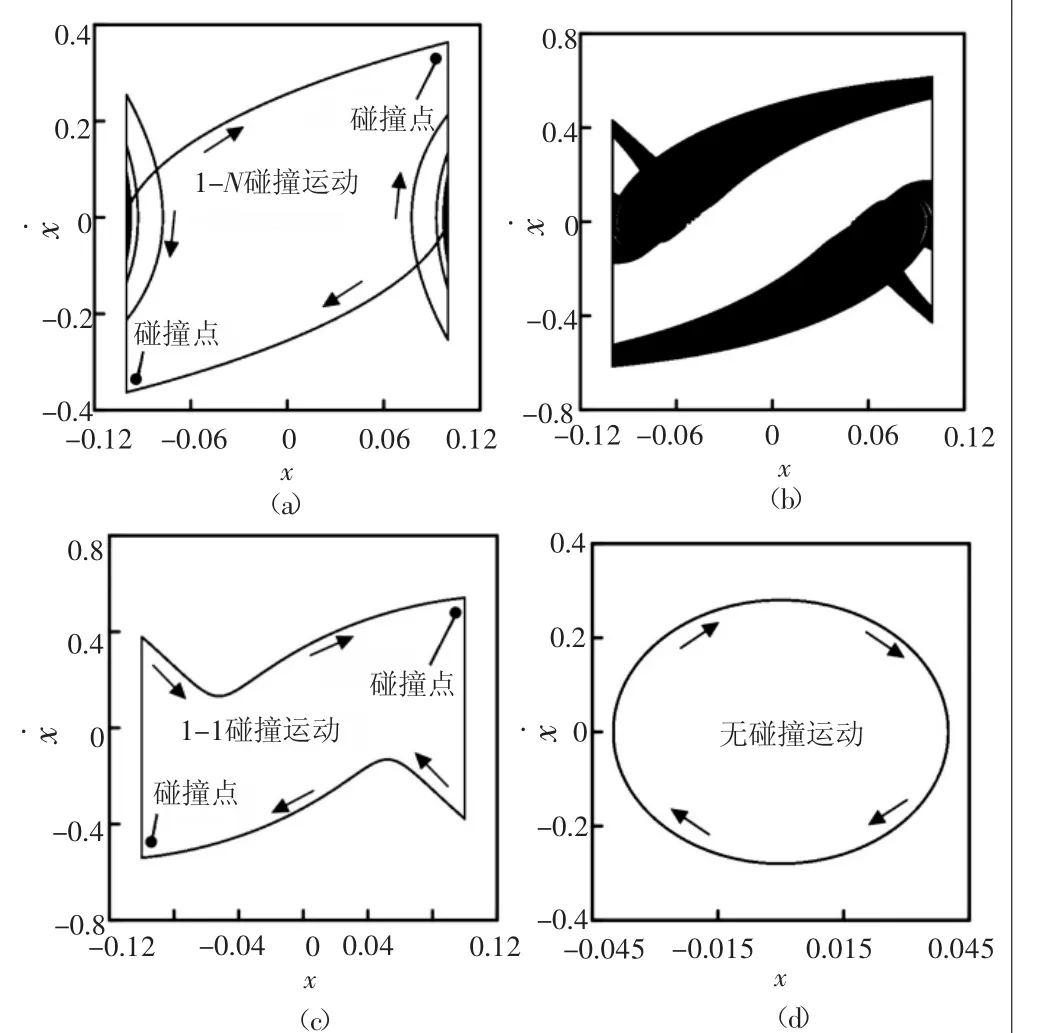
图5 刚性碰撞振动相图

选取系统参数：ξ=1.0,ξ1=0.5,ξ2=0.5,d=0.2,R=0.1,k1=1.0,k2=1.0,设定初始值：x1=x˙1=0，以σ作为Poincaré截面，激振频率ω为分岔参数，系统全局分岔如图6所示。结合分岔图与相平面图说明弹性碰撞运动对噪声的影响。选取激振频率ω=2.0, 弹性碰撞振动系统稳定在相平面运动轨迹如实心箭头所示，左右两侧为约束面，当质块运动到左侧与约束面发生第一次碰撞，经过碰撞后速度发生阶跃改变，在周期激励的作用下质块与左侧约束面接着发生第二次碰撞，在此激振力作用下，质块与左侧约束面发生两次碰撞，按照对称的约束，同样质块与右侧约束面发生两次碰撞，碰撞的次数越多，因碰撞发出声响的次数越多，系统运动相图如图7（a）所示；随激振频率增加到ω=2.5时，质块与左右约束面各发生一次碰撞，经过碰撞后质块速度减弱，当第二次与约束面接触时发生了擦边运动，弹性碰撞振动系统运动相图如图7（b）所示；当激振频率增加到ω=3.0时，质块与左右约束面各发生一次碰撞后，随后进入了滑动运动，弹性振动系统运动相图如图7（c）所示；当激振频率增加到ω=3.25时，质块在相平面稳定运动轨迹如实心箭头所示，质块与约束面无碰撞发生，表示质块不会与约束面碰撞产生声响，弹性碰撞振动系统运动相图如图7（d）所示。在车辆系统运动中，尽量能够避免多次碰撞产生的高频次声响，降低或避免端门滑道与导轨之间的相互碰撞，消除噪声提高舒适性。

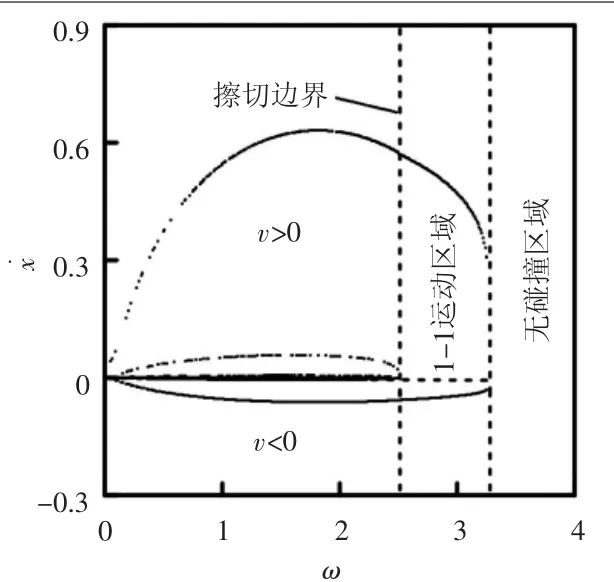
图6 弹性碰撞系统全局分岔图

4 结 论

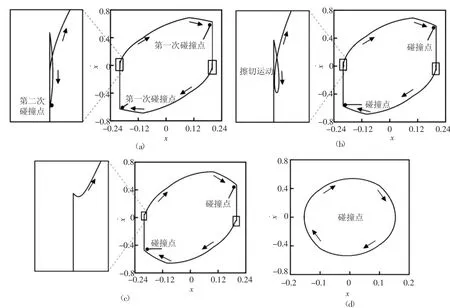
图7 弹性碰撞振动运动相图

本文以车辆端门系统为模型建立两种不同类型的单自由度含间隙的碰撞振动系统动力学模型，采用数值仿真，结合分岔图与相平面图解释碰撞与噪声之间的联系。通过对比分析两种系统运动特性，刚性碰撞运动系统运动情况复杂，产生的混沌运动、多周期运动可以反映出质块与约束面之间的碰撞次数，碰撞次数越频繁从而产生声响的频次更高，当系统运动处于混动运动状态下，将会是高频次的碰撞噪声，另外刚性碰撞系统运动产生碰撞振动的周期激振频率范围更宽，更容易产生复杂碰撞声响。弹性碰撞系统相对于刚性系统运动情况，非线性碰撞振动运动稳定性更好，发生碰撞运动的周期激励频率范围窄，因碰撞产生的声响频次降低，从而更有利于改善端门下滑道与导轨之间因碰撞产生的噪声。