谈儿童数学教育视角下“模型思想”建立的策略
□张秋爽
数学有三大基本思想:抽象思想、推理思想和模型思想。很多教师感到困惑:模型思想到底是什么?数学建模、数学模型和模型思想三者的关系是什么?如何在教学中进行实践和有意识地融入模型思想?
一、合理把握小学数学模型思想的定位
《义务教育数学课程标准(2011 年版)》指出:“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。建立和求解模型的过程包括:从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律,求出结果并讨论结果的意义。这些内容的学习有助于学生初步形成模型思想,提高学习数学的兴趣和应用意识。”
数学模型方法是指将具体的数学问题情境化,建立相应的数学模型,并解决问题的一种思想方法;模型思想是模型方法的理论升华,它强调对实际问题情境的抽象和概括,即把实际问题抽象简化为由各种数学符号组成的普通表达式、公式、运算法则、已知定理等数学模型;数学建模是一个过程,从具体的情境出发,发现数学问题,发现规律,建立数学模型,进一步验证和完善数学模型,最后应用数学模型。
所以教师在教学中要立足学生实际,让学生参与建模的全过程,进一步促进学生对概念的理解,提高学生解决问题的能力。
二、数学模型思想建立的策略
(一)挖掘可以渗透模型思想的素材,做到有意识
小学数学教材中有很多内容都可以渗透模型思想。张奠宙先生说:“广义地讲,数学中各种基本概念和基本算法都可以叫作数学模型,加、减、乘、除都有各自的现实原型,它们都是以各自相应的现实原型作为背景抽象出来的。”因此,作为教师要根据教学内容有意识地挖掘模型思想,并在教学实践中以恰当的方式加以落实,而不仅仅局限于让学生记忆概念、掌握解题方法,更应提高学生运用所学知识方法解决问题的能力,培养学生的应用意识和创新意识,增强他们用数学的思维来观察世界和解决问题的能力。
如十进制计数法是表示整数和小数的基本模型;整数四则运算是数学运算的基本模型,其基础是运算意义和位值思想;常见的量是表述数量单位的基本模型,其核心是度量,体现的是计量单位和个数之间累加的结果;平均分派物品的数学模型是分数,比、分数和除法的模型就是“份”。
小学阶段有两个基本的数量关系,也是两个典型的模型“路程=速度×时间”“总价=单价×数量”,它们的基础都是乘法意义和四则运算之间的关系。
用字母表示数是代数学的本质,也是代数学的基本模型。天平从本质上说是等量关系的“直观模型”,方程是表示一类等量关系的模型;正、反比例是表示一类具有变量关系的模型。
点、线、面、体是几何图形的基本模型,认识图形从图形的大小、形状、位置和方向四个方面进行;刻画图形有两个维度,一个是特征的维度,一个是度量的维度。
图形位置的模型是维度和坐标系,前、后、左、右、上、下是一年级学习表示位置的词语。一维空间的刻画需要三对词语中的一对,如前、后;二维空间的刻画需要三对词语中的两对,如前、后、左、右;三维空间的刻画需要三对词语。学生借助坐标轴和方向标,辨别东、南、西、北、东南、东北、西南、西北八个基本方位。在小学高年级,学习在方格纸上用数对表示位置,这实际上就是解析几何的模型;方格纸和数对,从本质上说是表示事物数量、位置、大小和数量关系的直观模型。
统计图表是收集和整理数据的工具,是表述数据分布情况的模型,统计量是分析和描述数据特征的模型,数据统计包括数据的收集、整理、分析和决策全过程。平均数是小学阶段统计量数学模型学习的开始。
烙饼问题、沏茶问题是对策论问题,田忌赛马问题属于运筹学问题,其模型是“做事情的顺序问题”;鸡兔同笼问题直接体现了假设和方程的思想;植树问题讨论的是“点—间隔”之间的关系。“植树问题”“路灯问题”“排队问题”“锯木问题”“爬楼问题”“敲钟问题”等都有着相同的数学结构,可以归为同一个数学模型,也就是间隔问题,即点和间隔依次重复出现,而且间隔长度不变。凡是属于这样的情况就是植树问题。单循环赛问题、握手问题就是数线段的模型;七桥问题就是“一笔画”问题的模型等。
不论是概念的学习、规律的探索,还是实际问题中解决问题策略的习得,抑或法则的得出、图形的抽象、知识的应用、数据的分析等内容,都有数学模型。换句话说,数与代数、图形与几何、统计与概率、综合与实践四个领域都有数学模型,而综合与实践更符合数学建模的过程,都要让学生在情境中参与,在实际操作中探索和经历模型的建立过程,有意识做好数学模型思想的融入与渗透,使学生知其然又知其所以然。
(二)参与数学建模的全过程,做到有感悟
一般情况下,学生参与的数学建模要经历创设情境—提出假设—建立模型—求解模型—验证模型—应用模型的全过程。吴正宪老师在教学乘法《乘法分配律》一课时,围绕三个核心问题展开教学。
问题1:如何从现实中激活模型的生活化意义?
教师给学生提供多个生活原型:求红花和黄花一共有多少朵?求种花的总面积是多少平方米?求客厅瓷砖的总面积是多少平方米?
问题2:如何从例证中体验模型的抽象化意义?
教师让学生列举多道等式,从乘法意义出发,体验模型的抽象化意义。
一般传统的课堂中,教师往往仅通过一个实际问题引出等式,而且出示实际问题的目的仅仅是为了让学生得到等式,便于学生进行模仿;但是“从现实生活或具体情境中抽象出数学问题”才是真实数学建模过程的首要环节。吴正宪老师的课堂从具体情境出发,给出了两个例子,她不急于让学生得出规律,而是借助情境和现实,拉长了学生对等式生活意义的体验过程,学生在充分的体验中激活了已有生活经验,对于等式中间蕴藏的规律在头脑中越来越清晰。在初步形成猜想后,下面的举例其实就是学生对其猜想的初步验证。
问题3:如何表征才能凸显模型的形式化意义?
教师选择学生中出现的典型的五种想法,有序地呈现出来。


学生通过不同的表征方法,建构模型的形式化意义。教师有层次地展示学生作品,让每个学生都能在黑板上找到自己的影子并积极地参与讨论,不断澄清认知的偏差,在自我否定、补充完善中,抽象出数学模型,感悟数学建模的过程。
听完吴正宪老师的课,笔者豁然开朗。教师上课一般只进行到第二个核心问题,新课就结束了,教师会留出更多的时间让学生大量地做习题,以巩固基础知识和基本技能。通过对比,我们发现,让学生经历模型建立的全过程,有利于学生对数学的进一步理解,探究问题中隐含的数学关系。
(三)在解决问题中应用模型,做到善提取、巧对接
数学模型的本质是从现实数学问题或现象中抽象出普适性的数学模型,进而应用数学模型解决实际问题。
学生在学习了线段、射线和直线之后,开始学习数线段问题。通过分类,可以得出图1中一共有6条线段“AB、BC、CD、AC、BD和AD”,既可以连线,也可以计算,算式:1+2+3=6。

图1
而数角和数三角形都属于同一个数学模型,都是先数出有几个基本图形,然后从1开始依次加到几。图2一共有6个角,图3一共有6个三角形。

图2
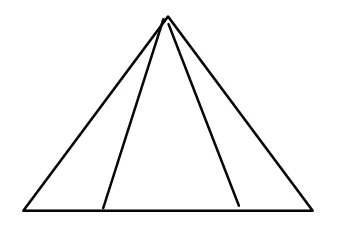
图3
当学生把数线段、数角和数三角形都看成具有相同结构的模型之后,还需要到现实生活中应用模型解决问题;其中的桥梁就是学生能面对新情境新问题对接所学概念、所建立的模型,从脑中提取出来。只要善提取、巧对接就解决了90%的问题。
面对数图形这类问题,现实生活中的情境还有:
(1)鼹鼠钻洞一共有( )条路线。

(2)有4 个好朋友寒假聚会,每个人要握一次手,一共需要握几次?
(3)有1,2,3,4 四个数,从中挑两个数作为乘法算式的两个因数,可以得到几个不同的积?
(4)有4支篮球队,要进行单循环赛,一共需要赛几次?……
其中鼹鼠钻洞的4 个洞口,抽象成4 个点,洞与洞相接的地方抽象成线,这样就变成了数线段问题。我们要求学生在解决问题时能写一写、画一画,就是想让他们把实际问题转化成数学模型。这四个问题,其中鼹鼠钻洞的4 个洞口、4 个好朋友、4 个数和4 支球队就是线段上的4 个端点;而所求问题鼹鼠钻洞的路线条数、握手的次数、几个不同的积和单循环赛的场次就是数线段模型,都是用1+2+3=6;这里的“3”就是三条基本线段,“2”是指两条相邻的线段组成的比较长的线段有2 条;“1”是指三条基本线段组成的一条最长的线段。
三、课堂教学中建立模型思想的建议
模型思想的建立需要一个循环往复的过程,需要从大量的问题情境或生活实例(具体形象、旧知识)中抽象出概念、法则、运算定律,再用自己的方式表达,最后用自己的方式解读。这也是一个建构和解构的过程,这两个过程缺一不可,共同承担学生建立模型思想的全过程。
教材中有很多内容属于模型思想,如植树问题、鸡兔同笼及一些基本的数量关系、函数等,建议大家进一步挖掘,做到前有孕伏,后有照应,加强学生对数学概念的理解,提升他们思考和做事的能力,尤其是在新情境下能够解决富有挑战性的问题。
教学中要让学生感悟模型无处不在,我们应从低年级起,恰到好处地结合日常教学对学生进行模型意识的渗透,体会建立模型、研究模型、应用模型是数学的本质。

