考虑径向温差的架空输电导线的动态增容分析

李军辉 贾思棋 杜冬梅 丁亮亮 何青 刘彬

摘   要：为提高输电线路输送能力和输电导线的动态增容，对输电线的径向温升现象进行研究分析. 以架空输电线为例，首先基于热平衡方程计算导线温度理论值，然后通过建立输电线温度场电磁耦合有限元绞合模型，计算输电线径向温度分布规律，研究不同因素的影响，最后结合温度场的分析结果，分析输电导线动态增容的效果，根据导线的温度分布计算最小的载流量. 结果表明：输电线的径向温度分布不均匀，内部温度高，表面温度低;输电导线温度受到载流量、风速、环境温度及时间变化的影响，径向温差一般可达0.58～4.53 ℃，因此研究架空导线的径向温差，根据导线的温度分布计算保证安全运行的最小载流量，有利于提高输电导线的动态增容，保证线路的运行安全.

关键词：输电导线;温度场;动态增容;有限元分析

中图分类号：TM751                           文獻标志码：A

Abstract：In order to improve the transmission capacity and the dynamic capacity increase of transmission line， the radial temperature rise phenomenon of transmission line is studied and analyzed. In this paper， the overhead transmission line is taken as an example. Firstly， the theoretical value of the conductor temperature is calculated based on the heat balance equation. Then， the electromagnetic coupling finite element stranding model of the transmission line temperature field is established to calculate the radial temperature distribution of the transmission line and study the influence of different factors on it. Finally， the effect of dynamic capacity expansion of the transmission line is analyzed based on the analysis results of the temperature field， and the minimum current carrying capacity is calculated according to the temperature distribution of the conductor. The results show that the radial temperature distribution of the transmission line is not uniform. The internal temperature is high and the surface temperature is low; the temperature of the transmission line is affected by  different current， wind speed， ambient temperature and time. The radial temperature difference can generally reach 0.58～4.53℃， so the radial temperature difference of the overhead conductor is studied. According to the temperature distribution of the wire， the minimum current carrying capacity is calculated， which is beneficial to improve the dynamic capacity of the transmission line so as to ensure the safe operation of the line.

Key words：transmission lines;temperature field;dynamic capacity;finite element analysis、

近年来，随着我国国民经济的高速发展，用电量不断增加，对架空输电导线的输电能力要求越来越高. 提高输电能力通常是架设新电路，或者升级改造电网，利用导线动态增容技术挖掘现有线路的输送潜力，投资小、见效快[1-2].

目前，研究架空输电导线运行温度以及动态增容的方法，大多采用以热平衡方程为基础的数值计算方法[3-6]和有限元分析法. ICE1597—1995[7]、摩尔根公式法、IEEE738标准[8]等均采用数值计算法. 林玉章[9]基于热平衡方程，以我国设计规范[10]为准，引入集肤效应系数以及铁损系数更精确地计算交直流电阻比，提高了导线温度计算的准确性;肖凯等[11]根据二维热传导控制方程，分析了输电导线的热量来源及散热量的问题，针对输电导线进行温度场的求解以及径向温差的计算，验证了径向温差的存在且不可忽略. 数值计算法并未考虑输电导线温度分布不均匀、各层温度并不等同的问题，对导线运行时的温度及载流量难以做到更准确的计算.

为了解决上述问题，赵成运等[1]通过建立架空输电导线模型，针对几种不同类型的导线进行温度场分析，环境温度一定时，分析输电导线温度、载流量、风速三者的关系;苏超等[12]在赵成运等[1]的基础上，建立了JL/LB1A-300/50钢芯铝绞线有限元模型，计算了不同气象环境条件下输电导线的温度场及径向温差;张世龙[13]认为输电导线温度分布并不均匀，数值计算预测的导线温度有一定的局限性，提出了基于有限元模型，计算瞬态导线温度的数值方法;刘刚等[14]通过对导线截面磁场及温度分布进行迭代计算，建立了有限元模型并搭建了实验台进行导线温度的测定，验证了有限元仿真结果的准确性. 上述 研究，在建立输电导线模型时分别作了不同程度的简化，均未考虑导线的空隙分布及绞合状态会影响导线温度分布这一问题.

动态增容技术是指在输电线路上安装一定的在线监测装置对导线状态（导线温度、张力等）以及气象参数（环境温度、光照强度、风速等）进行检测[15]. 张启平等[16]根据风速、环境温度、光照强度等参数，采用IEEE数值计算法确定输电导线载流量，进行动态增容的研究，并未考虑径向温差的存在;严有祥

等[17]通过将光纤测温与护层电流检测结合，对导线温度载流量进行了计算，但仅考虑了导线表面温度，而导线在运行状态下温度分布并不均匀，仅测量导线的表面温度有一定的局限性.

基于以上背景，本文以架空输电导线为例，基于热平衡方程介绍载流量以及复合散热系数的计算方法，以LGJ240/30为例，建立架空输电导线三维实体绞合有限元模型，与IEEE的理论计算值进行比较，通过电磁-热耦合有限元模型研究输电导线径向温度分布规律以及不同因素的影响，最后结合温度场的分析结果，分析输电导线动态增容的效果，根据导线的温度分布计算最小载流量，以保证线路的运行安全.

1   输电导线温度场计算原理

1.1   热平衡方程

架空输电导线因暴露在空气中，散热量和吸热量均会受到外界环境的影响，其散热主要有对流散热、辐射散热、电流发热以及日照吸热4部分组成[18]，如果风速增大，会增加导线与外界环境的热交换，从而增大输电导线的散热量. 为了更直观地表示输电导线的吸热和散热量与各因素之间的关系，导线温度影响因素示意图如图1所示. 其中实线表示环境温度、日照、电流和风速直接影响导线温度，进一步也会影响导线弧垂;而虚线表示日照对环境温度产生影响，环境温度对风速产生影响.

根据热平衡方程，导线载流量为[19]：

式中：I为导线允许载流量，A;qc为单位长度导线的对流散热功率，W/m;qr为单位长度导线的辐射散热功率，W/m;qs为单位长度导线的日照吸热功率，W/m;Rac为最高允许工作温度下导线的交流电阻，Ω/m.

对流散热由自然对流散热、强制对流散热组成. 自然对流散热指在没有外部作用力的情况下，空气和导线之间通过温度差使空气发生流动，从而发生的传热;强制对流散热指在外部作用力下使空氣流动，带走导线周围的热量，从而降低导线温度.自然对流的冷却能力较差，可以等价为风速0 m/s的强制对流，对流散热量为：

1.3   复合散热系数计算

对流散热（qc）和辐射散热（qr）是钢芯铝导线最主要的两种散热方式，根据体积散热率不变的原则[21]，可确定导线表面的复合散热系数α，即：

α =     （19）

式中：A为单位长度绞线的侧表面积，m2.

2   钢芯铝绞线模型

2.1   导线模型

钢芯铝绞线是输电架空导线中最常见的导线，外部由单层或多层铝股线绞合在钢芯周围，既保证了良好的导电能力，又保证了导线的强度.

选取LGJ-240/30型架空导线进行有限元建模分析，其几何参数如表1所示[22].

表1   导线LGJ-240/30 几何参数

Tab.1   Wire LGJ-240/30 geometric parameters

[层 股数 股线直径/mm 节径比 节距/mm 捻角/（°） 1 1 2.4 — — — 2 6 2.4 20 157.5 5.7 3 9 3.6 15 181.2 10.5 4 15 3.6 14 244.5 12.4 ]

注：层1和2为钢芯;层3和4为铝股.

根据几何参数对其进行建模，并将基本参数设置[23]为：直流电阻Rdc = 0.118 1 Ω/km，铝绞线的电阻率ρa =2.8×10-8 Ω·m，钢芯的电阻率ρs =20×10-8Ω·m，铝线的导热系数ka = 237 W/（m·K），钢芯的导热系数ks = 80 W/（m·K），空气的导热系数由导线的平均温度以及环境温度确定，光照强度S=1 000 W/m2. 划分单元时，采用三角形网格单元对导线实体进行网格划分，导线有限元模型见图2.

[0.000][0.013][0.025][0.038][0.050（m）]

（a）整体

[0.01][0][0.005][0.015][0.02（m）]

（b）横截面

图2   钢芯铝绞线的有限元模型

Fig.2   Finite element model of steel-cored

aluminum stranded wire

2.2   验证

以LGJ-240/30型号导线为例验证有限元模型. 环境温度为20 ℃，风速为0 m/s，载流量为400 A时，对A、B、C、D、E共5组不同数量的网格进行有限元计算，做网格无关性检验，检验结果如表2所示.

表2   导线网格无关性检验结果

Tab.2   Mesh independence test result of wire

[组 网格数量/个 计算值/℃ 理论值/℃ 偏差/% A 223 238 59.56 62.22 -4.28 B 258 794 60.75 62.22 -2.36 C 322 550 61.23 62.22 -1.59 D 440 326 61.88 62.22 -0.55 E 453 316 61.88 62.22 -0.55 ]

由表2可以看出，当网格数量低于440 326时，检测结果与网格数量高于440 326时有一定偏差;网格数量高于440 326时，检测结果基本趋于一致. 网格数量越多，计算周期越长，因此在保证精度的前提下，认为D组网格数量满足极端低温环境下导线温度需求，网格划分示意图如图2所示.

风速为0 m/s，载流量单位步长取50 A，变化范围在250～450 A之间，分析导线的温度分布规律，并将计算结果与IEEE理论计算结果进行对比，对比结果如表3所示.

由表3可知，风速为0 m/s时，数值模拟结果与理论计算值误差较小，最大误差仅为7.90%，该误差在工程允许范围内，说明本文建立的导线温度场有限元模型是正确的. 另外，与理论计算方法相比，有限元模型考虑了导线内空气间隙、股间接触和对流散热条件，更真实地反映了导线的径向温度分布规律.

3   计算结果与分析

3.1   架空导线径向温度场分析

3.1.1   自然对流条件下导线的径向温度场分析

风速为0 m/s，载流量单位步长取50 A，变化范围在250～450 A之间，分析导线的径向温度分布情况. 以载流量300～400 A为例，对自然对流条件下导线径向温度场进行分析.

由图3可知，导线最高温度出现在内层铝线处，内部钢芯温度次之，外层铝股温度最低. 主要原因有：1） 铝的单位体积发热率远大于钢的发热率，所以铝股的热量较高，且铝股又把一部分热量传给内部钢芯; 2） 内部钢芯远离空气对流边界，导线内又有空气间隙的存在，因此散热较慢，温度较高;3） 虽然铝股产生更多的热量，但外层铝股却和空气直接进行热量交换，因此散热最多，温度最低.

3.1.2   强制对流条件下导线的径向温度场分析

风速为0.5 m/s，载流量单位步长取50 A，变化范围在250～450 A之间，分析导线的径向温度分布情况. 以载流量300～400 A为例，对强制对流條件下导线径向温度场进行分析.

由图4可知，导线的径向温度分布规律在有风条件和无风条件下基本一致，中心温度高，表面温度低. 载流量一定时，强制对流下的导线温度低于自然对流下的导线温度，并且，导线的径向温度分布是不均匀的，因为空气间隙改变了导线的散热路径.

3.1.3   导线各层温度分布分析

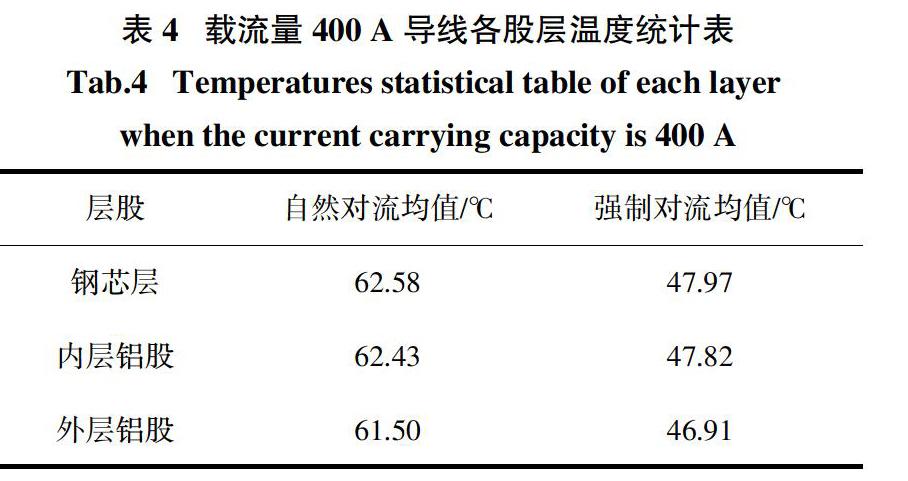
导线各层温度分布遵循一定规律，但各层股线的接触情况及大小存在差异，导致导线各层股线温度分布不均匀. 为了解导线各层股线温度分布规律，以风速为0 m/s，载流量为400 A为例，通过计算各股层间温度均值和温度方差，对其在自然对流和强制对流条件下各股层温度进行对比分析.

由表4可知钢芯层的平均温度最高，温度变化很小，可以用相同的温度表示;内层铝股的平均温度接近钢芯层的平均温度，但易受绞合线之间实际接触条件的影响，温度变化量明显增大;外层铝股的平均温度最低，被绞合线之间实际接触条件和外界对流情况联合影响，温度方差最大，说明外层铝股的温度变化最大.

3.2   导线径向温度场的影响因素

3.2.1   载流量

本文选取工况为常温（环境温度为20 ℃），光照强度为1 000 W/m2，风速为0 m/s，载流量从250～450 A范围内以50 A的步长变化，分析载流量对导线径向温度场的影响.

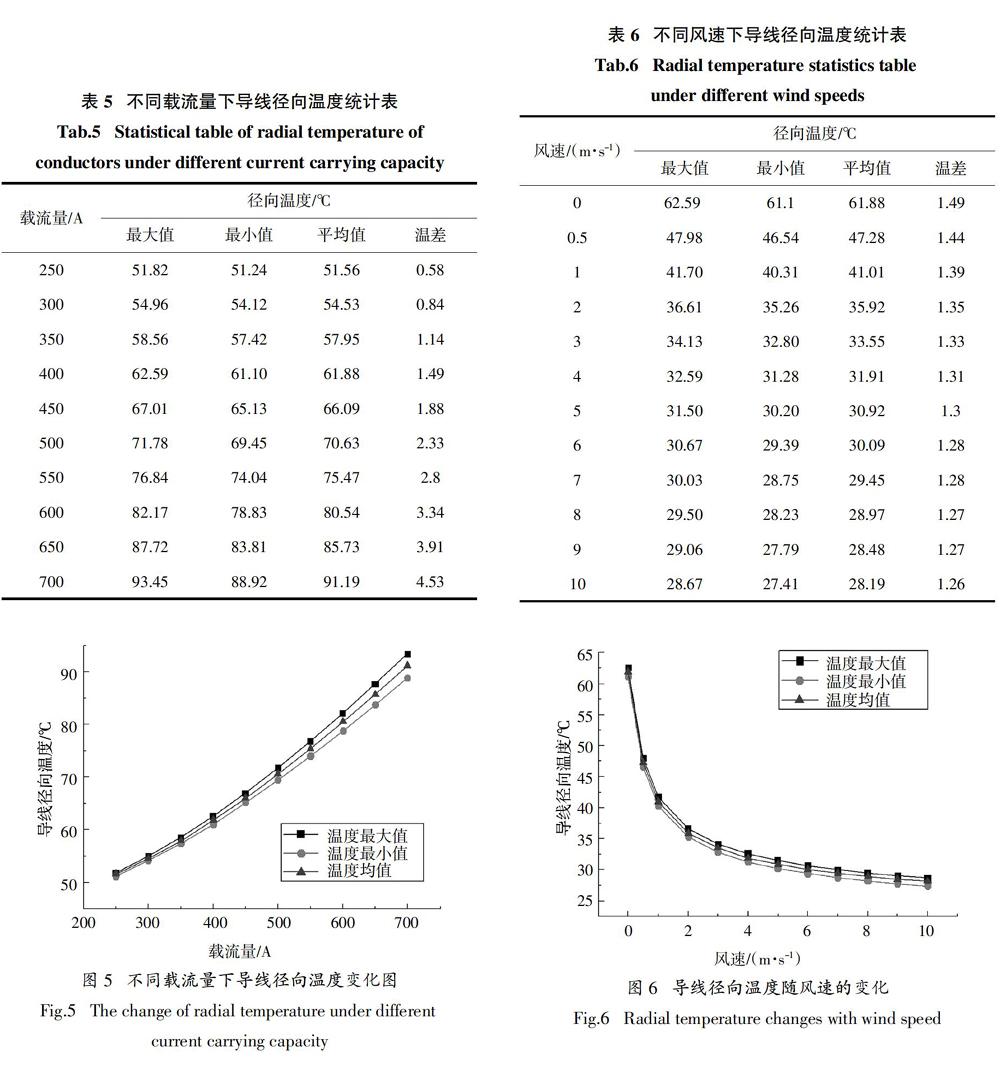
由表5及图5可知，风速为0 m/s时，导线的径向温差随载流量的增加而增大，温差从0.58 ℃增大到4.53 ℃. 另外，载流量越大，导线的径向温度变化量越大.

3.2.2   风速

本文选取工况为常温（环境温度为20 ℃），光照强度为1 000 W/m2，载流量为400 A，风速单位步长取1 m/s，范围在0、0.5 m/s、1～10m/s之间，分析风速对导线径向温度场的影响.

由表6及图6可知，当导线的载流量不变时，导线径向温度受环境温度影响较大. 风速为0～5 m/s时，温度迅速变化，温度下降了30.96 ℃;风速为5～10 m/s时，温度下降平缓，温度下降了2.73 ℃. 特别是风速为0.5 m/s时，温度的变化最快.

3.2.3   环境温度

风速为0 m/s时，光照强度取1 000 W/m2，载流量取400 A，环境温度的单位步长为10 ℃，在-20～20 ℃之间变化，分析环境温度对导线径向温度场的影响.

由表7及图7可知，环境温度与导线温度之间的关系近似呈线性. 环境温度每升高1 ℃，导线径向温度升高约0.94 ℃. 环境温度的升高，提高了导线内空气的导热性，导线内部的热量可以更好地与外界空气流通，因此导线的温升略小于1 ℃.

3.2.4   时间

风速为0 m/s时，载流量取400 A，环境温度和光照强度按北京某年夏至日气温和光照强度取值，如图8所示. 分析时刻变化对导线径向温度场的影响如表8及图9所示.

由表8、图9可知，导线径向温度随时间的变化呈先增加后减小的趋势，在13：00左右达到最大值. 是因为一天中光照强度呈正态分布，但是环境温度却在14：00左右达到最大值，因此一天内导线温度不再呈正态分布.

3.3   基于温度场的导线载流量分析

3.3.1   导线径向温差对载流量计算的影响

为了讨论导线径向温差对载流量计算的影响，本文以表5即不同载流量下导线径向温度的变化为例，分析径向温差对导线载流量的影响. 分别以导线的温度最大值和温度最小值，计算得到导线允许的载流量如表9所示.

表9   导线径向温度最大值及最小值时的载流量

Tab.9   Current carrying capacity at maximum

and minimum radial temperature

[载流量/A 径向温差/℃ Imax /A Imin /A （Imax - Imin） /A 250 3.12 275.27 266.63 8.64 300 3.80 318.04 307.17 10.87 350 4.54 360.99 347.96 13.03 400 5.33 403.75 388.48 15.27 450 6.20 445.99 428.53 17.46 ]

由表9可知，由导线温度最小值（外层铝股处）和温度最大值（内层铝股处）计算导线允许载流量差值可达8～17 A，约占导线本身载流量的3.46%～3.88%. 在实际线路中，导线温度在线监测多测量的是表面温度，因此以导线的表面温度来调整载流量是不安全的.

3.3.2   环境条件对载流量计算的影响

环境温度为20 ℃、光照强度为1 000 W/m2的条件下，当导线温度为70 ℃和80 ℃，风速变化时对应的导线载流量如表10所示. 其中，70 ℃代表的是我国电网安全运行时的电流阈值，80 ℃代表了电网故障时的电流阈值.

3.4   基于温度场的导线动态增容

文献[16]选择500 kV瓶武5905线作为实验电路，设立了环境温度、日照强度、风速3个工况进行实时监测. 假设导线允许运行温度不变，根据实时测量线路的实际风速、日照强度以及环境温度来确定导线的载流量，充分挖掘导线的输送容量.

根据文献[16]夏季测点数据，假设导线允许运行温度为70 ℃，分别选取最高环境温度、最高光照强度、自然对流情况下最高环境温度和最高光照强度4种情况进行分析计算，这4种情况的氣候参数几乎为测点中最恶劣的，此时运行的导线载流量最小. 选取光照强度为1 000 W/m2，风速为0 m/s，环境温度为40 ℃作为载流量理论值进行计算，如表12所示.

由表12可知，4种工况中，载流量最大值和最小值相差约11 ～100 A，载流量最小值相对理论值增容率约53.62%～203.60%. 由于理论值计算采用的环境参数仅为我国最恶劣环境计算参数，因此，根据实际输电线路环境参数确定载流量，是提高输电线路输送容量的有效方法. 现行动态增容方法主要针对导线表面温度进行检测，但导线同层温度分布并不均匀，因此仅采用导线表面温度进行监测并不完全可靠. 考虑径向温差可以更准确地计算输电导线的最小载流量，在保证安全运行的状态下，提高导线输送容量.

4   结   论

1）与IEEE计算方法相比，建立导线三维实体模型，进行有限元分析，能更准确地反映导线内部的气隙和接触，了解径向温度分布规律.

2）考虑到导线由不同金属材料组成且内部存在空气间隙等复杂情况，对流条件下的径向温度分布不均匀，中心温度高，表面温度低;强制对流条件对导线径向温度分布影响不大，但增加了导线的散热，使导线整体温度显著降低.

3）通过对导线各层温度分析可知，钢芯层的平均温度最高，温度变化很小，可用相同的温度表示;内层铝股的平均温度接近钢芯层的平均温度，但容易受到绞合线之间实际接触条件的影响，温度变化量明显增大;外层铝股的平均温度最低，受绞合线之间实际接触条件和外界对流情况的联合影响，温度方差最大，说明外层铝股的温度的变化最大.

4）以LGJ240/30型导线为例，根据有限元仿真分析，得到导线温度最大值和最小值，分别进行载流量计算，差值可达8～17 A，占导线本身载流量的3.46%～3.88%. 在实际线路当中，导线温度在线监测多测量的是表面温度，因此以导线的表面温度来调整载流量是不安全的.

5）导线温度受载流量、风速、环境温度以及时间变化不同程度的影响，径向温差一般为0.58～1.88 ℃. 当风速恒定时，导线的径向温差随载流量的增大而逐渐增大;当载流量恒定时，导线的温度随着风速的增大而快速下降;环境温度与导线温度之间的关系近似为线性的，环境温度升高1 ℃，导线温度约升高0.94 ℃.

6）环境条件对导线允许的载流量有显著的影响. 风速为0.5 m/s比风速为0 m/s时，载流量提升约121～170 A，增加约20.29%～36.08%，因此风速对导线允许载流量的影响较大;当环境温度从20 ℃变为-20 ℃时，载流量减少约42.15%～55.05%，因此环境温度对导线载流量的影响是不能忽视的.

7）根据实际输电线路环境参数确定载流量，在工况条件较为恶劣时，载流量最大值与最小值相差11 ～100 A，载流量最小值相对理论值增容率约为53.62%～203.60%. 相比静态计算而言，考虑径向温差的输电导线动态增容可更准确地计算导线的最小载流量，有效提高输送容量.

参考文献

[1]    赵成运，郑良华，田春光，等. 66 kV架空输电线路导线温度场的数值计算分析[J]. 吉林电力，2007，35（5）：5—8.ZHAO C Y，ZHENG L H，TIAN C G，et al. Numerical calculation on conductor temperature field of 66 kV overhead transmission lines [J]. Jilin Electric Power，2007，35（5）：5—8. （In Chinese）

[2]    杜运兴，卢心龙，聂逸悠. 线路覆冰分层脱落动力响应的研究[J]. 湖南大学学报（自然科学版），2017，44（7）：109—115. DU Y X，LU X L，NIE Y Y. Research on dynamic response of layer shedding in line system [J]. Journal of Hunan University（Natural Sciences），2017，44（7）：109—115. （In Chinese）

[3]    何青，李军辉，张暕，等. 分裂导线覆冰的数值分析与实验研究[J]. 中南大学学报（自然科学版），2019，50（6）：1485—1491.HE Q，LI J H，ZHANG J，et al. Numerical analysis and experiment of icing condition of bundled conductors [J]. Journal of Central South University（Science and Technology），2019，50（6）：1485—1491. （In Chinese）

[4]    LIU G，LI Y，QI K，et al. Sag calculation difference caused by temperature difference between the steel core and outer surface of overhead transmission lines [C]// 2016 Australasian Universities Power Engineering Conference （AUPEC）. Brisbane，Australia：IEEE，2016：1—5.

[5]    ZE?CZAK M. Approximate relationships for calculation of current-carrying capacity of overhead power transmission lines in different weather conditions[C]// 2017 Progress in Applied Electrical Engineering （PAEE）. Koscielisko，Poland：IEEE，2017：1—5.

[6]    趙喆. 高压架空输电线路动态增容风险评估研究[D]. 南京：南京理工大学自动化学院，2017：21-36.ZHAO Z. Researches on risk calculation for dynamic capacity increase of overhead lines [D]. Nanjing：College of Automation，Nanjing University of Science And Technology，2017：21—36. （In Chinese）

[7]   IEC 1597—1995 Overhead electrical conductors-Calculation methods for stranded bare conductors [S]. Suisse：Bureau Central de la Commission Electrotechnique Internationale，1995：1—85.

[8]  IEEE 738—1993 IEEE Standard for calculating the current-temperature relationship of bare overhead conductors [S]. New York：The Institute of Electrical and Electronics Engineers，Inc，1993：1—56.

[9]    林玉章. 高压架空输电线路载流量和温度计算[J]. 南方电网技术，2012，6（4）：23—27.LIN Y Z. The calculation of current carrying capacity and temperature of high voltage overhead lines [J]. Southern Power System Technology，2012，6（4）：23—27. （In Chinese）

[10]  GB 50545—2010 110 kV～750 kV架空输电线路设计规范[S]. 北京：中国计划出版社，2010：15—23.GB 50545—2010  code of design of 110 kV～750 kV overhead transmission line[S]. Beijing：China Planning Press，2010：15—23. （In Chinese）

[11] 肖凯，刘永斗，李鹏云. 架空导线径向温度场的数值模拟[J]. 武汉理工大学学报，2015，37（4）：65—70.XIAO K，LIU Y D，LI P Y. Numerical simulation of radial temperature field of overhead conductors [J]. Journal of Wuhan University of Technology，2015，37（4）：65—70. （In Chinese）

[12]  苏超，武小梅，谢海波. 架空输电线路温度和最大允许载流量计算[J]. 宁夏电力，2016（6）：1—6，13.SU C，WU X M，XIE H B. Calculation of temperature and maximum allowable load flow of overhead transmission lines [J]. NingXia Electric Power，2016（6）：1—6，13. （In Chinese）

[13]  张世龙. 输电导线截面不均匀温度场的有限元模拟[J]. 电力学报，2018，33（6）：64—72.ZHANG S L. ERM simulation on heterogeneous temperature field of transmission lines [J]. Journal of Electric Power，2018，33（6）：64—72. （In Chinese）

[14]  刘刚，李炀，陈垣，等. 基于电磁-热耦合模型的架空导线温度分布和径向温差的计算与实验验证[J]. 电力系统保护与控制，2018，46（7）：7—13.LIU G，LI Y，CHEN Y，et al. Calculation and experimental verification of temperature distribution and radial temperature of overhead transmission line based on electromagnetic-thermal coupling fields [J]. Power System Protection and Control，2018，46（7）：7—13. （In Chinese）

[15]  韩晓燕. 增容技术在电网系统中的应用及现状简析[J]. 时代汽车，2018（10）：188—189.HAN X Y. Brief analysis of application and status quo of compatibilization technology in power grid system [J]. Auto Time，2018（10）：188—189. （In Chinese）

[16]  張启平，钱之银. 输电线路实时动态增容的可行性研究[J]. 电网技术，2005，29（19）：18—21.ZHANG Q P，QIAN Z Y. Study on real-time dynamic capacity- increase of transmission line [J]. Power System Technology，2005，29（19）：18—21. （In Chinese）

[17]  严有祥，朱婷，王蕾，等. 新型输电电缆动态增容系统设计与应用[J]. 电力系统及其自动化学报，2018，30（8）：133—139.YAN Y X，ZHU T，WANG L，et al. Design and application of new type dynamic capacity enlargement system for transmission cable [J]. Proceedings of the CSU-EPSA， 2018，30（8）： 133—139. （In Chinese）

[18]  高琦. 架空导线温度场的数值模拟与分析[D]. 北京：华北电力大学能源动力与机械工程学院，2017：33-34.GAO Q. Numerical simulation and analysis of temperature field of overhead conductors [D]. Beijing：School of Engergy Power and Machanical Engineering，North China Electric Power University，2017：33—34. （In Chinese）

[19]  徐建坤. 架空导线微风振动强化换热效应及疲劳寿命分析[D]. 郑州：郑州大学土木工程学院，2019：89—95.XU J K. Enhanced heat transfer effect and fatigue life analysis of overhead conductor under Aeolian vibration [D]. Zhengzhou：College of Civil Engineering，Zhengzhou University，2019：89—95. （In Chinese）

[20]  戈东方. 电力工程电气设计手册[M]. 北京：中国电力出版社，1989：20-27.GE D F. Electrical engineering electrical design handbook [M]. Beijing：China Electric Power Press，1989：20—27. （In Chinese）

[21]  黄新波，崔运涛，朱永灿，等. 输电导线冰棱覆冰表面换热系数分析[J]. 高电压技术，2019，45（6）：1975—1981.HUANG X B，CUI Y T，ZHU Y C，et al. Analysis of the surface convective heat transfer coefficient of icicle on transmission lines [J]. High Voltage Engineering， 2019， 45（6）： 1975—1981. （In Chinese）

[22]  GB 1179—2008圆线同心绞架空导线[S].北京：中国标准出版社，2008：1—40.GB 1179—2008 round wire concentric stranded overhead conductor [S]. Beijing：Standards Press of China，2008：1—40. （In Chinese）

[23]  刘红军，周佳林，赵亚新. 基于断线作用的输电塔线体系动力效应影响分析[J]. 湖南大学学报（自然科学版），2018，45（3）：62—71.LIU H J，ZHOU J L，ZHAO Y X. Analysis on dynamic effect of transmission line system based on wire breakage [J]. Journal of Hunan University（Natural Sciences），2018，45（3）：62—71. （In Chinese）