渗流区简化方法对闸基渗流计算结果的影响分析

丁秀英，余晗硕

（1.黄河水利职业技术学院，河南 开封 475004；2.南水北调中线干线工程建设管理局，北京 100038）

0 引言

《水闸设计规范》（SL265-2016）规定，土基上水闸基底渗透压力计算可采用改进阻力系数法或流网法［1］。 改进阻力系数法是在阻力系数法、独立函数法、分段法等基础上发展起来的，具有较高精度的近似流体力学的方法，被广泛应用。在应用改进阻力系数法进行水闸防渗计算时， 闸基地下轮廓线的简化给部分工程技术人员带来一定的困惑。 笔者试以河南省郏县梁庄拦河闸为例， 对闸基地下轮廓线不同简化方法的渗流计算结果进行对比分析， 以期供相关技术人员参考。

1 工程概况

梁庄拦河闸是20 世纪70 年代建造的， 原为5孔水力自控翻板闸门， 主要任务以灌溉为主。 枯水期，关闭闸门，可以抬高闸上游水位，增加河道拦蓄水量，补充地下水，利于灌溉；汛期，打开闸门，可以保证安全下泄上游洪水。 2012 年，有关部门对该闸进行安全鉴定， 发现其泄洪能力已不能满足防洪要求，需对其进行除险加固。2014 年，相关单位对梁庄拦河闸进行了重建。 重建后的梁庄拦河闸采用平板钢闸门，为Ⅲ等工程，永久的主要建筑物工程等级为3 级，设计洪水标准为20 年一遇，最大过闸流量为950 m3／s，枯水期正常蓄水位为103.37 m，拦蓄水量为20 万m3，设计灌溉面积为2 500 亩。 该闸闸址处，地震动峰值加速度为0.05 g，地震设计烈度为Ⅵ度。经技术、经济指标综合比选后，拟定除险加固的具体方案为：新建拦河闸共有7 孔，闸室分三联，其中边联为2孔、中联为3 孔。 闸门尺寸（宽×高）为5.5 m×4.0 m。 闸室段长为15 m，底板顶面高程为99.87 m，底板厚1.5 m，上、下游齿墙宽、深均设为1.5 m，板桩长为5 m。 上下游水位差ΔH＝3.5 m。闸室铺盖段长为20 m，采用混凝土结构，上、下游均设置浅齿墙，齿墙宽、深均设为0.5 m。 消力池底板厚度拟定为1.2 m， 下设导渗反滤层。 梁庄拦河闸防渗布置如图1 所示。

2 闸基地下轮廓线的简化

根据图1 可计算出该水闸闸基地下轮廓线的垂直投影长度S0＝8 m，水平投影长度L0＝35 m。

2.1 简化方法一

图1 水闸防渗布置图（单位：m）Fig.1 Sluice impermeable layout （Unit：m）

对闸基地下轮廓线的内部倾斜段简化后， 将其分为14 段，如图2 所示，分段名称和编号如表1 所示。 经计算得知， 地下轮廓线各段长度分别为：L1＝0.8 m、L2＝0.5 m、L3＝0.5 m、L4＝18 m、L5＝0.5 m、L6＝0.5 m、L7＝5.2 m、L8＝3.0 m、L9＝1.5 m、L10＝1.5 m、L11＝9.0 m、L12＝1.5 m、L13＝1.5 m、L14＝1.5 m。

图2 简化方法一闸基地下轮廓线简化图（单位：m）Fig.2 Simplified outline of sluice base underground configuration of method No.1 （Unit：m）

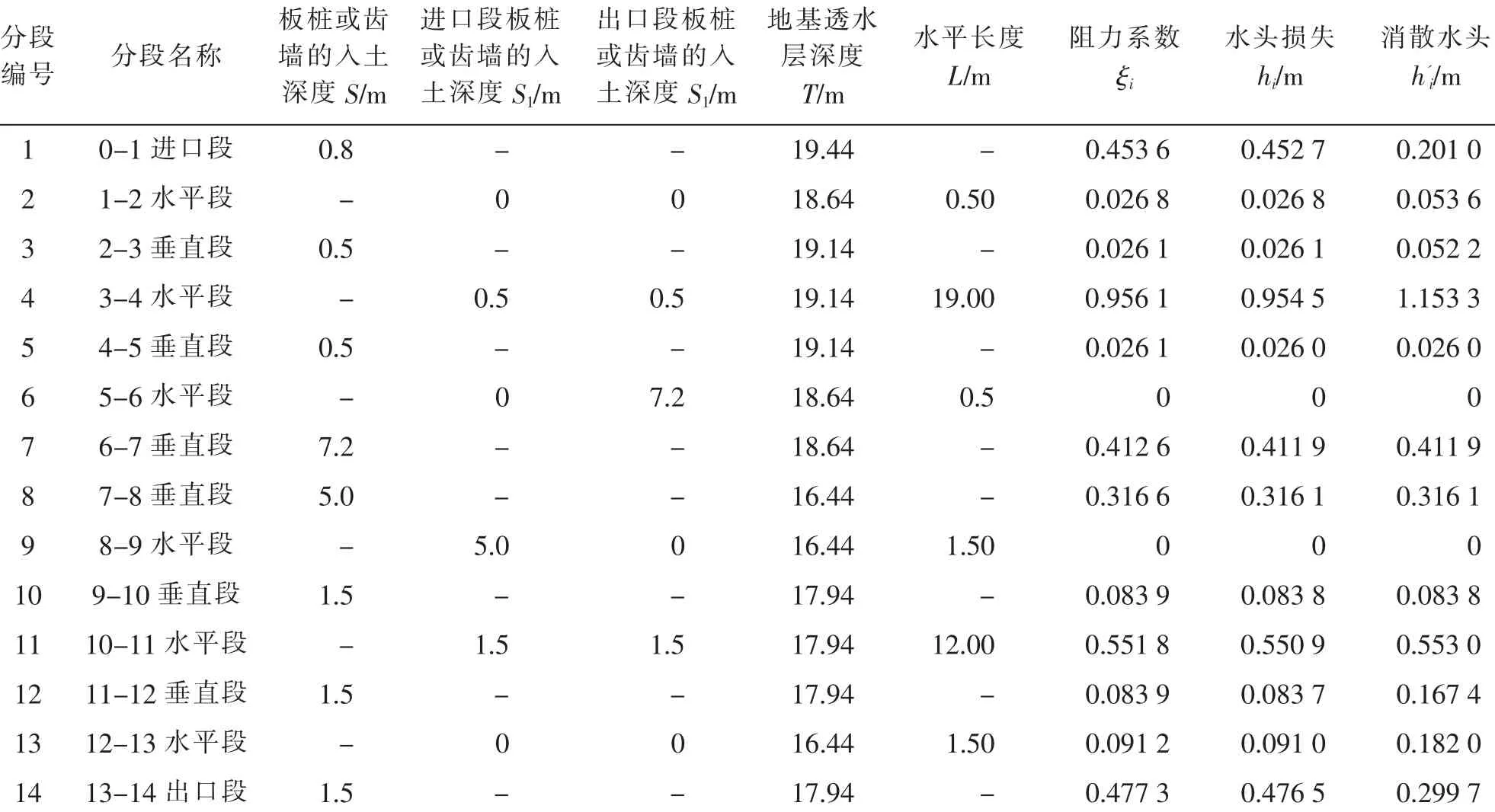
表1 简化方法一各段渗透压力水头损失Tab.1 Seepage pressure water head loss of each section of simplified method No.1

因L0/S0＜5，所以土基上水闸的有效深度Te按公式（1）计算［2］。

式中：Te为水闸的有效深度，m；L0为地下轮廓的水平投影长度，m；S0为地下轮廓的垂直投影长度，m。

经计算，Te＝19.44 m。 因T实际＝20 m＞19.44 m，所以，地基透水层计算深度取19.44 m。

地基透水层计算深度确定后， 计算各段的阻力系数。

（1）进、出口段阻力系数。进、出口段的阻力系数可用式（2）计算［3］。

式中：ξ1为进、 出口段的阻力系数；S 为板桩或齿墙的入土深度，m，此处取0.80；T 为地基透水层计算深度值，m。

（2）水平段的阻力系数。水平段的阻力系数可按式（3）计算［4］。

式中：ξ2为水平段的阻力系数；Lx为水平段长度，m；S1、S2分别为进、 出口段板桩或齿墙的入土深度，m，此处均为0；T 为地基透水层计算深度，m。

（3）垂直段的阻力系数计算。垂直段的阻力系数可用式（4）计算［5-6］。

式中：ξy为内部垂直段的阻力系数；S 为板桩或齿墙的入土深度，m；T 为地基透水层计算深度，m。

经计算，各段的阻力系数如表1 所示。 进、出口段阻力系数修正如表2 所示。

2.2 简化方法二

对闸基地下轮廓线的内部倾斜段和闸底板上游齿墙进行简化， 并将地下轮廓线分为12 个典型流段，如图3 所示，分段名称和编号如表3 所示。 地下轮廓线各段长度分别为：L1＝0.8 m、L2＝0.5 m、L3＝0.5 m、L4＝18 m、L5＝0.5 m、L3＝0.5 m、L7＝5.2 m、L8＝3.0 m、L9＝12.0 m、L10＝1.5 m、L11＝1.5 m、L12＝1.5 m。 各段渗透压力水头损失计算方法同前，计算结果如表3 和表4 所示。

表2 简化方法一进、出口段的水头损失修正表Tab.2 Water head loss correction of inlet and outlet sections of simplified method No.1

图3 简化方法二闸基地下轮廓线简化图（单位：m）Fig.3 Simplified outline of sluice base underground configuration of method No.2 （Unit：m）

表3 简化方法二各段渗透压力水头损失Tab.3 Seepage pressure water head loss of each section of simplified method No.2

表4 简化方法二进、出口段的水头损失修正表Tab.4 Water head loss correction of inlet and outlet sections of simplified method No.2

2.3 简化方法三

将闸基地下轮廓线的内部倾斜段和闸底板上游齿墙简化后， 将地下轮廓线分为10 个典型流段，如图4 所示， 分段名称和编号如表5 所示。 经计算可知， 地下轮廓线各段长度分别为：L1＝0.8 m、L2＝0.5 m、L3＝0.5 m、L4＝19 m、L5＝5.2 m、L6＝3.0 m、L7＝12.0 m、L8＝1.5 m、L9＝1.5 m、L10＝1.5 m。 各段渗透压力水头损失计算方法同前，计算结果如表5 和表6 所示。

图4 简化方法三闸基地下轮廓线简化图（单位：m）Fig.4 Simplified outline of sluice base underground configuration of method No.3 （Unit：m）

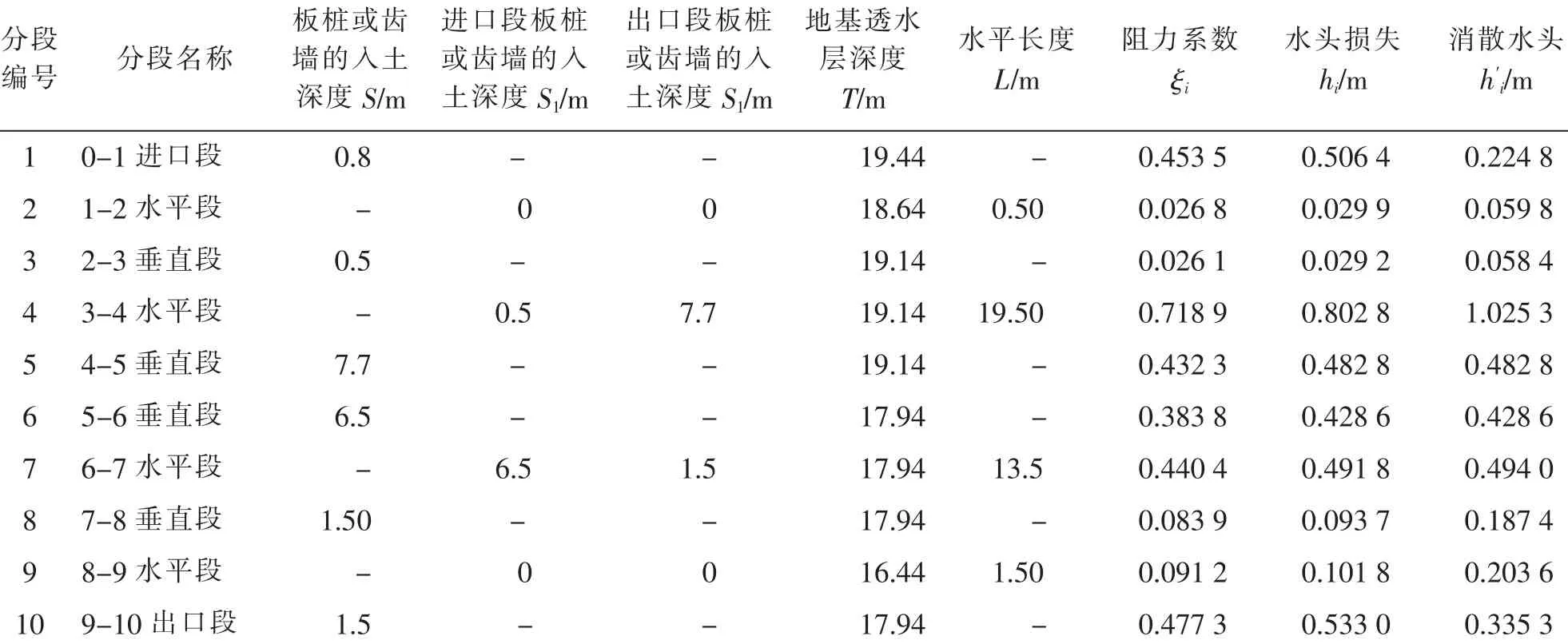
表5 简化方法三各段渗透压力水头损失Tab.5 Seepage pressure water head loss of each section of simplified method No.3

表6 简化方法三进、出口段的水头损失修正表Tab.6 Water head loss correction of inlet and outlet sections of simplified method No.3

2.4 三种简化方法的比较

针对上述三种简化方法，用式（5）计算闸基渗流各段的渗透压力和坡降，结果如表7 所示。

式中：J 为渗透压力坡降；L 为水平长度，m；h′i为消散水头值，m。

表7 三种简化方法各段水力坡降值对比情况Tab.7 Hydraulic slope value comparison of each section of three division methods

由表7 可以看出， 简化方法一划分的段数较多（14 段），与工程实际吻合度较高，计算结果较准确，但计算相对复杂。 简化方法二划分了12 段，与实际地基情况有差别，与简化方法一相比，其内部垂直段7-8 段和水平段10-11 段的水力坡降分别减少了16.129 0%和37.785 0%， 其余9 段的水力坡降增加了3.731 3%～3.874 7%。 简化方法三划分了10 段，计算也更简单了，但简化变形较大，与实际情况差别较大，其中内部垂直段7-8 段、内部水平段3-4 段、水平段10-11 段的水力坡降分别减少了9.677 4%、15.756 6%、32.899 0%，垂直段6-7 段的水力坡降增加了6.944 4%，其他6 段的水力坡降增加值均大于11.567 2%。

3 结语

利用改进阻力系数法进行水闸基底和侧向渗流计算时，地下轮廓线和绕渗轮廓线可适当简化，但不宜过分简化， 尤其是闸底板上游齿墙和铺盖下游侧齿墙部分的划分不易简化。否则，将对水力坡降的计算结果影响很大，从而使计算数据失真，以致造成水闸渗流稳定分析判断错误。