基于EEMD-LSTM 的区域能源短期负荷预测

（上海电力大学 自动化工程学院，上海 200090）

0 引言

随着全球能源需求的不断增长，化石能源日益短缺[1]。为缓解能源危机，减小环境污染带来的影响，新能源发电越来越受关注。2011 年，美国学者杰里米·里夫金（Jeremy Rifkin）在其著作《第三次工业革命》中，以新能源技术和信息技术的深入结合为特征，首次提出能源互联网的概念[2]。能源互联网包括广域能源互联网和区域能源互联网，广域能源互联网一般承担远距离的大型输电，连接两地大型能源基地；区域能源互联网作为能源互联网的重要表现形式，主要进行近距离输配电，多用于经济开发区、工业园区、电动汽车充放电等[3]。能源互联网主要由天然气、风电、光伏、储能提供电热，因此推进了多种能源形式协同运行，通过燃气内燃机、燃气轮机、风光发电以及生物质能发电，实现了能源的梯级利用和优势互补，符合“融合”“统一”“高效”“清洁”的理念[4]。能源互联网以其强大的耦合性为可再生能源产业发展提供保障，同时也成为智能电网的重要组成部分。

针对电网的可靠运行问题，很多学者进行了相关研究。文献[5]介绍了神经网络的特点，说明了能够有效处理电力短期负荷预测数据的非线性变化问题。文献[6]能够达到较高的精度，但其优化寻优算法考虑的因素较多，模型复杂，训练时间长，给实际应用带来困难。文献[7-8]采用人工神经网络对负荷参数模型进行预测，但是精度不够理想。文献[9]采用改进的遗传算法搜索全局最优值，以优化极限学习机算法等建立负荷预测的模型，预测结果基本可以满足精度要求，但预测模型考虑了较多因素，模型构建复杂。文献[10]对配电网进行负荷预测，并对不同层数的神经网络模型进行了对比，结果显示对于差异性较大的模型尚不能达到最优效果。文献[11-12]阐述深度学习在电力负荷预测中的应用，列举了常用的深度学习算法，对比分析之后验证出LSTM（长短期记忆神经网络）算法具有较高的精度，能够较好地预测负荷的短期功率，因此本文算例分析中采用LSTM 算法进行建模。文献[13]提出了一种改进的最小二乘向量机负荷预测模型，但模型预测结果依然存在较大误差，无法保证整体相对平稳的预测精度。

与大电网相比，区域能源互联网负荷随机性很强，历史负荷曲线相似度低，基本没有规律可循；并且用户容量有限，各用户间负荷特征不够明显。本文算例分析中采用EEMD（集合经验模态分解）方法对原始数据进行分解，能够有效避免模态混叠现象[14]；同时基于LSTM 较精准的预测效果，利用LSTM 对EEMD 方法得到的每个分量分别进行预测，以获得更好的预测结果。

1 EEMD 方法

EEMD 由EMD（经验模态分解）加入白噪声后改进得出。对于非平稳数据，不需要考虑其他因素影响，可以使用EMD 方法得到一组能够表现信号特征的数据。与小波变换等方法相比，这种方法是直观的和自适应的。因为分解是基于信号序列时间尺度的局部特征，而EEMD 作为一种白噪声辅助分析方法，在原始信号中加入多组随机的白噪声信号，能够更有效地降低原始序列的波动性，其分解过程如图1 所示。利用EEMD 方法可以将能源互联网负荷序列分解成数个相对平稳的分量。相比于小波分析，EEMD 不需要对信号进行预先分析和研究，而是直接进行分解。

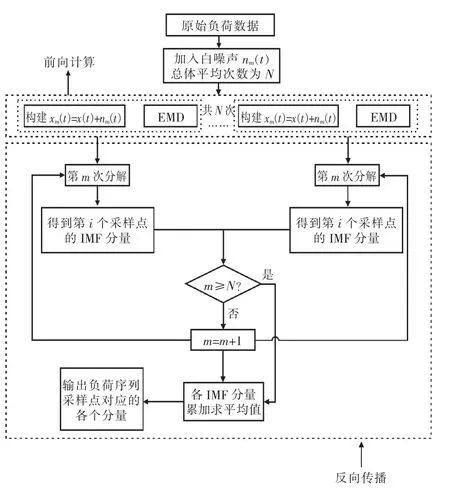
图1 EEMD 过程

在本次模型建立中，将能源互联网原始负荷序列x（t）中加入随机白噪声序列nm（t），得到加入噪声信号后的待处理序列：

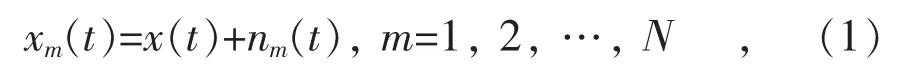
式中：N 为EMD 总体平均次数。

运用EMD 方法加入100 组有差别的随机白噪声序列，标准差取0.2。将区域能源互联网原始负荷序列分解一次之后再加入均方根相等的白噪声序列，经过N 次EMD，使信号重构达到较好的效果。通过此次分解，原始数据68 个典型日的采样点共得到了7 个IMF 分量和1 个剩余分量，也就是区域能源互联网原始负荷序列的EEMD结果。EEMD 能够克服基函数无自适应的问题，把时间序列分解成若干个IMF 分量和残余项R（t），即某个时刻采样点的数值等于对应的各个IMF分量与残余项相加。

2 LSTM 算法

为了解决RNN（循环神经网络）在处理长期依赖性时产生的梯度消失问题，提出了在RNN 基础上的改进算法LSTM，该算法在每个隐藏层中引入栅极和存储单元的概念。一个LSTM 内存块主要由输入门、遗忘门、输出门和自连接存储单元4 个部分组成。输入门控制对存储单元的激活输入，能够学习如何过滤和输出到连续网络的激活单元。遗忘门帮助网络忘记过去的输入数据并重新设置记忆细胞，由sigmoid 单元将权重设置为0 和1 之间的值：当权重为0 时，表示将上一状态的信息全部舍弃；当权重为1 时，表示将上一状态的信息全部保留。此外，应用乘法门使存储单元可以长时间访问和存储信息，每个单元中都包含存储前一时刻信息的记忆细胞。因此，LSTM 作为一种深度神经网络，具有更多的隐藏层，增加了计算的精度优势。LSTM 的典型结构如图2 所示，单个LSTM 神经元的预测结构如图3 所示。LSTM 记忆细胞的运算过程为：

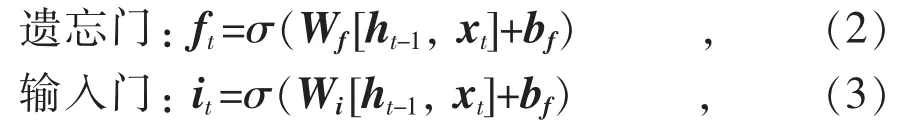
候选时刻记忆单元状态：

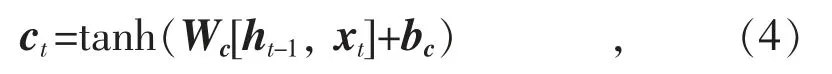
当前时刻记忆单元状态：

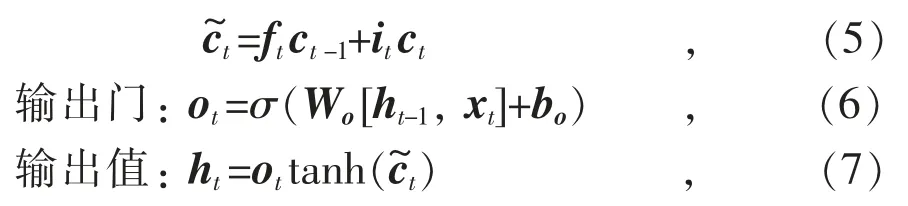
式中：Wf，Wi，Wc，Wo分别为遗忘门、输入门、细胞状态、输出 门的权重矩阵；bf，bi，bc，bo分别为对应的偏置矢量；xt为输入值；σ 为sigmoid函数；下标t 表示当前时刻，t-1 表示前一时刻。

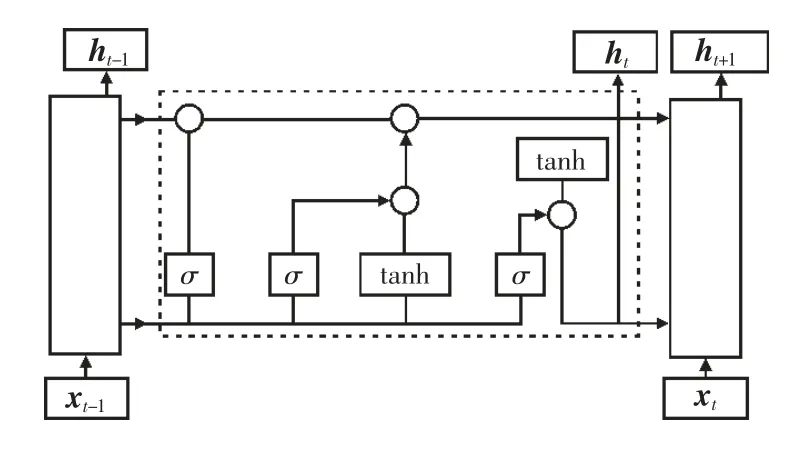
图2 LSTM 典型结构

从图3 中可以看出，LSTM 包括各个向量的交互，使得结构相比于单一的神经网络具有更多的层级。图中“＋”表示矩阵相加，“×”表示矩阵相乘。在进行负荷预测时，结合当前时刻的负荷输入值与前一时刻的负荷输出值赋予不同的权重矩阵和偏置矢量，使用tanh 函数和sigmoid 单元进行细胞状态的更新。本次试验设置隐藏层数为2，采用前48 个时刻预测后24 个时刻，训练集和测试集设置比例为7：3。首先利用EEMD 方法对原始负荷数据进行分解，得出一组具有不同特征的分量；然后将分解后的各个分量分别送入LSTM 进行预测；最后将各个分量值累加，得到预测结果。

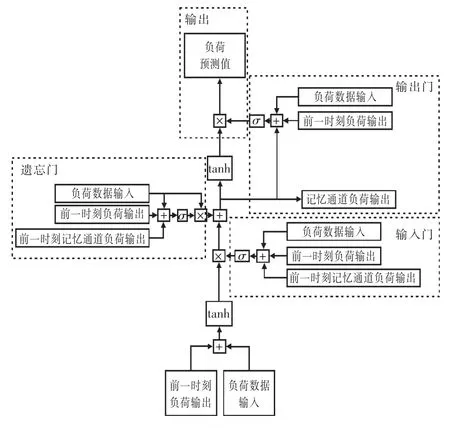
图3 单个LSTM 神经元的预测结构

3 基于EEMD-LSTM 的预测模型建立

本文提出基于EEMD-LSTM 的区域能源互联网系统日前小时负荷预测模型，对应流程如图4所示。对于历史区域能源互联网小时出力序列，首先采用EEMD 方法分解得到一组分量，每个分量数据归一化到[0，1]范围内，然后建立对应的LSTM 模型进行预测，将结果进行反归一化，并叠加各个分量即日前区域能源互联网系统小时负荷预测值，最后将输出的预测结果与原始负荷数据进行对比，并进行误差分析。

为了更直观地对比预测结果，本次算例选用预测结果误差分析常用的APE（相对百分比误差，量符号为EAP）进行作图分析，对比各个算法的误差结果。使用MAPE（平均绝对百分比误差，量符号为EMAP）、MSE（均方误差，量符号为EMS）和RMSE（均方根误差，量符号为ERMS）分别对预测结果进行评估，各个误差的表达式分别为：

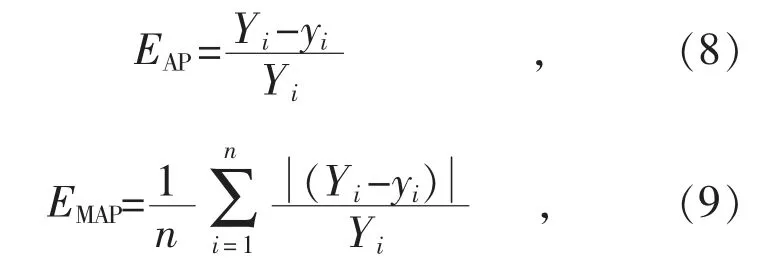
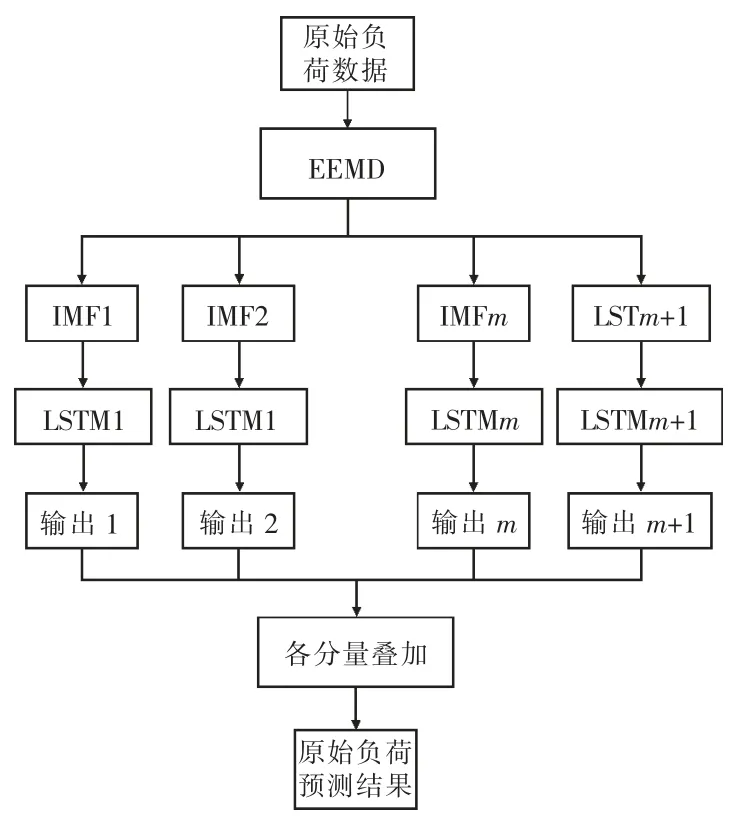
图4 EEMD-LSTM 流程

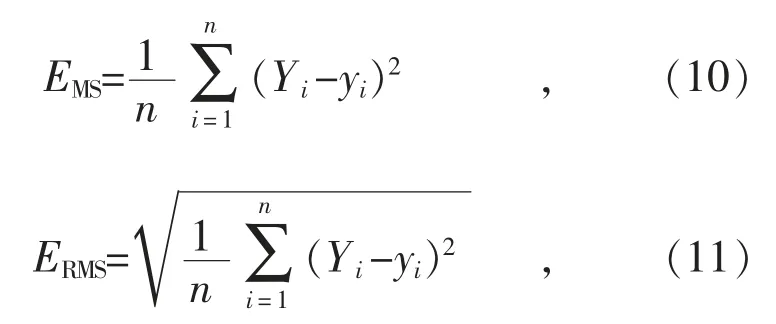
式中：n 为数据总个数；Yi为第i 个实际值；yi为第i 个预测值。

4 算例分析

本文以某区域能源互联网系统各单元总负荷数据为研究对象，选取2017 年1 月1 日00：00 至2017 年3 月9 日24：00，共计68 个典型日，采样时间间隔为1 h，共计1 632 个点。LSTM 的迭代次数设置为100 次，隐藏层数为2，训练集和测试集设置比例为7：3。寻找最优的预测模型之后，把预测样本作为输入值代入最优模型中并得到2017 年3 月9 日的预测值。采用EEMD 方法对原始负荷序列进行分解，结果如图5 所示。

通过图5 各个分量图可以更直观地看出，所有IMF 分量均反映出频率从高到低的不同尺度的系统负荷序列波动特性。IMF1 的平均振幅小，在所有分量中频率最高，并且规律性不明显，可以判断为负荷序列中的随机分量；IMF2—IMF4具有较好的规律性，周期性较为明显，而且曲线的幅值随着时间的推移有所增长，可以反映出负荷序列的局部波动情况，因此这些IMF 分量可判定为负荷序列的细节分量；其余的IMF 分量和余量R（t）的平均振幅大，具有很好的周期性和规律性，尤其是余项反映了负荷曲线的全局变化趋势，因此IMF5—IMF7 以及余量R（t）为负荷序列的趋势分量。

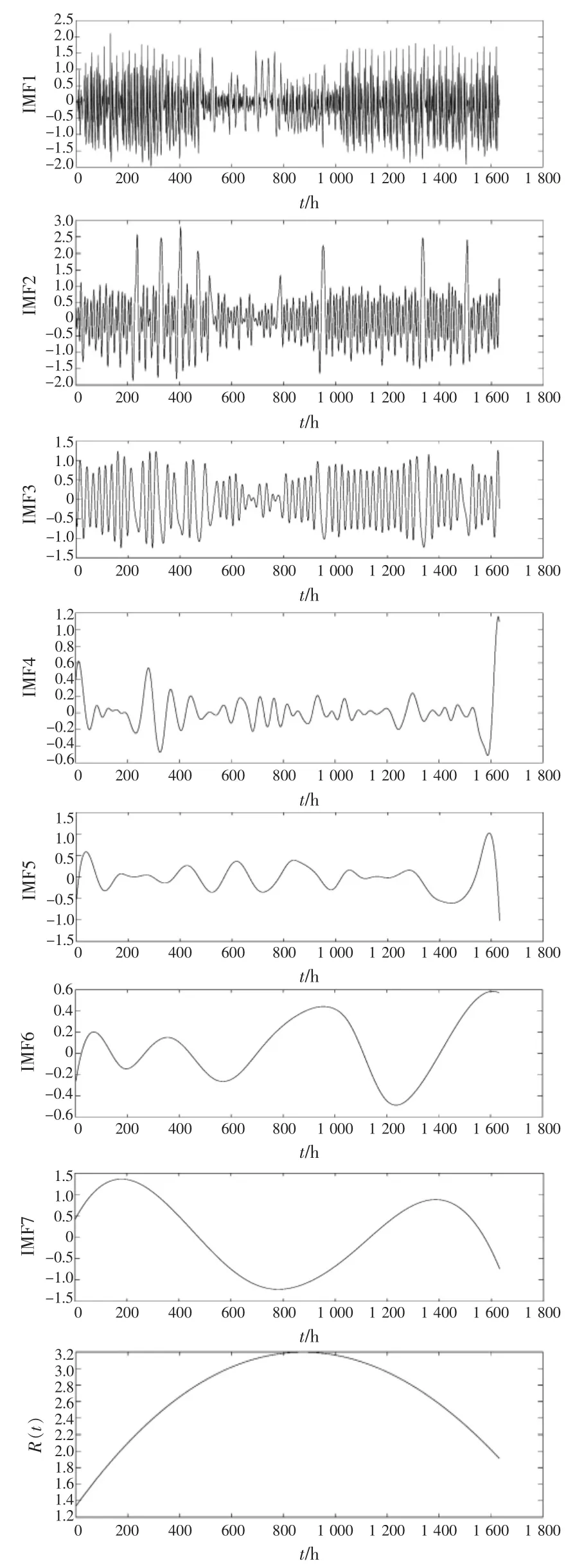
图5 原始负荷数据的EEMD 结果

为了验证本文预测模型的可行性，选取了另外3 种模型与其进行对比，其中一个模型采用单一的LSTM，另一个模型采用EMD-LSTM 算法，最后一个为其他的单一神经网络模型——Elman神经网络。选取2017-01-01 T 00：00—03-09 T 24：00 期间，时间间隔1 h 的采样点，共计1 632个点。对后24 个采样点进行预测，即对3 月9 日00：00 —24：00 采样点数据进行对比分析。预测结果如图6 所示，预测相对误差如图7 所示，预测误差数据对比见表1。

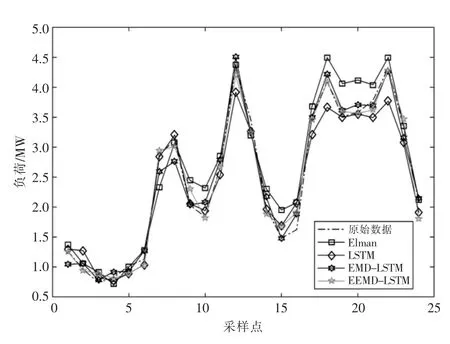
图6 系统3 月9 日负荷预测结果（采样间隔1 h）

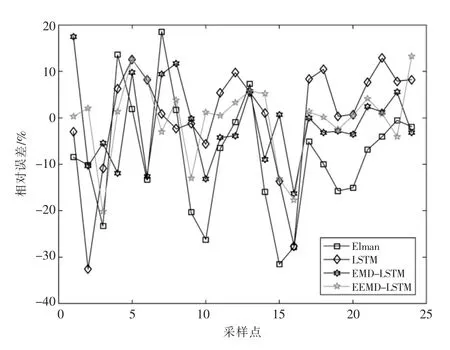
图7 系统3 月9 日负荷预测相对误差对比（采样间隔1 h）

由图7 可以看出，EEMD-LSTM 算法的相对误差波动性较小。由表1 可以看出，采用EEMDLSTM 模型的预测精度最高，其MAPE 和MSE 比其他模型的值都要小，验证了LSTM 算法的可行性，同时证明了EEMD 方法能降低原始序列的非平稳性对预测精度的影响。

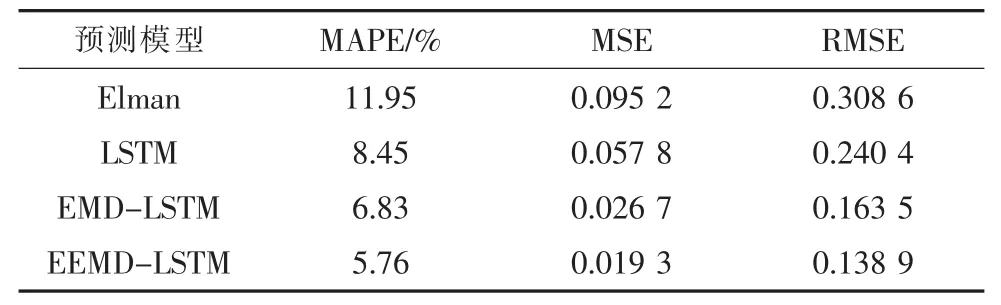
表1 系统负荷预测误差数据对比（采样间隔1 h）

由表1 可以看出，单一神经网络进行比较时，LSTM 的预测精度比Elman 要高，加入白噪声运用EEMD 方法进行原始负荷数据分解后，能够克服EMD 方法分解的不足，预测精度有明显提高。从整体来看，基于EEMD-LSTM 算法的预测结果很少出现相对误差极大的点。而另外两种模型的预测结果中，往往会出现较多相对误差极大的“失真点”。采用MAPE，MSE 和RMSE 作为评价指标，算例分析得出的值越小，说明模型的预测精度越高。

为了验证本文提出算法的有效性和适用性，使用间隔15 min 采样点进行预测对比。现仍采用2017-01-01 T 00：00—03-09 T 24：00 期间，时间间隔为15 min 的采样点，共计6 528 个点。对后24 个采样点进行预测，即对3 月9 日19：00—24：00采样点数据进行对比分析。预测结果如图8 所示，为便于与前例对比分析，误差预测结果如图9 所示，预测误差数据对比见表2。

由表1 和表2 对比分析可以得出，数据量由1 632 个采样点增大到6 528 个采样点时，EEMDLSTM 构造的预测模型的精度最高。同时，验证了在单一算法中LSTM 相对于Elman 的优越性。在组合预测中，EEMD-LSTM 能够比EMD-LSTM取得更好的效果，算法对比表明了EEMD-LSTM的优越性。

使用同时段的数据，采样时间间隔15 min，共计6 528 个采样点，预测3 月9 日全天的负荷预测值，结果如图10 所示。训练集与测试集比例不变，将迭代次数增加至150 次，EEMD-LSTM模型的MAPE 维持在3.5%左右，进一步验证了数据量增大时EEMD-LSTM 算法的优越性。由于预测点增多，需要扩大预测的维度及增加迭代次数。当需要预测的点增加时，精度会有所下降，计算时间也会增长。但相比于原始数据采样点较少时的预测结果来说，当数据量增大时，EEMDLSTM 的预测结果能够达到更精准的效果。

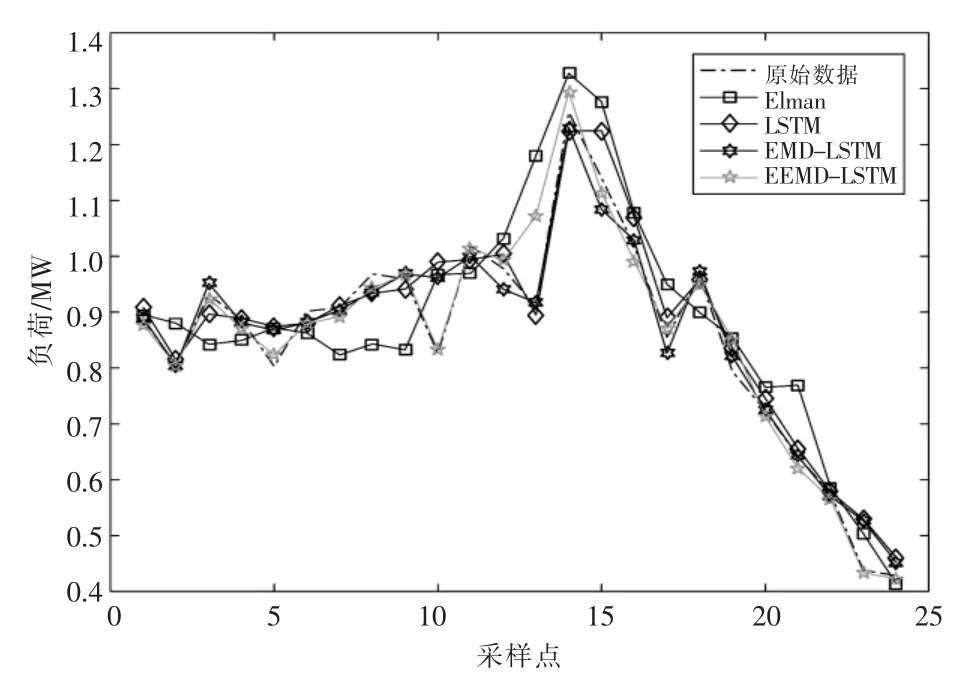
图8 系统3 月9 日19:00—24:00 负荷预测结果（采样间隔15 min）

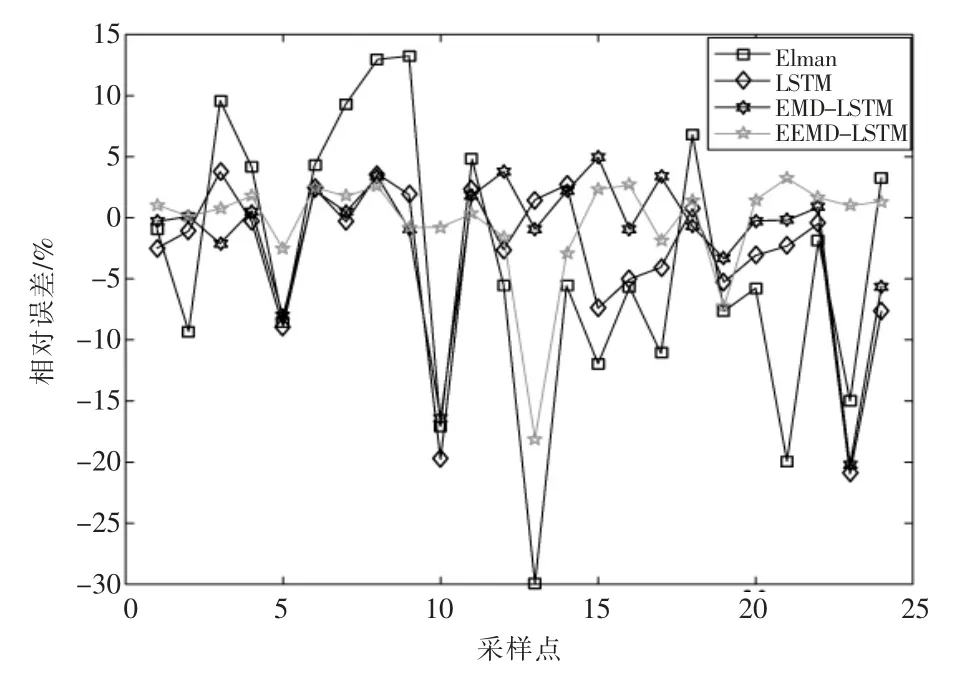
图9 系统3 月9 日19:00—24:00 负荷预测相对误差对比（采样间隔15 min）

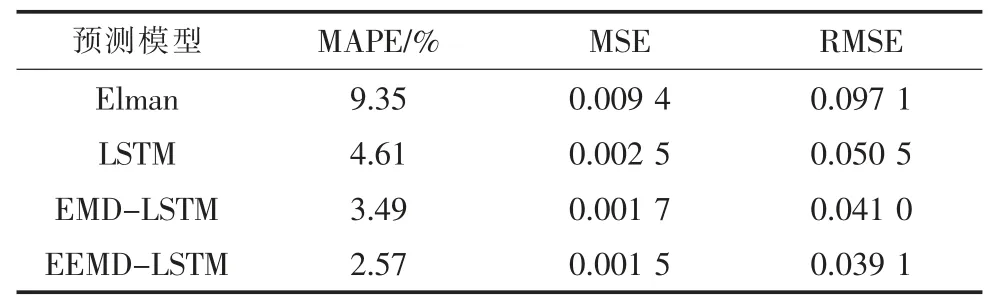
表2 预测误差数据对比（采样间隔15 min）

5 结语

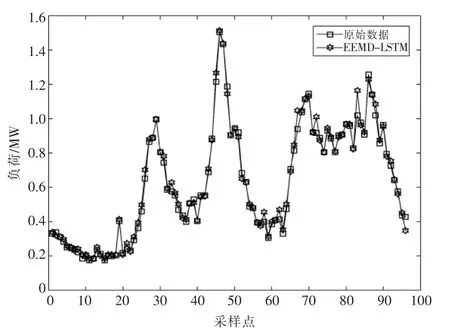
图10 系统3 月9 日全天负荷预测结果（采样间隔15 min）

针对区域能源互联网发电短期负荷功率预测的准确性问题，本文提出了一种基于EEMDLSTM 算法的区域能源互联网系统小时负荷预测模型。EEMD-LSTM 模型能够有效克服原始信号中的不确定因素，并且利用LSTM 存储单元长时间学习和保留电力负荷历史数据中的有用信息，并使用遗忘门将无用信息去除，然后将EEMD 得出的每一个分量送入LSTM 算法中进行预测，对结果进行叠加处理后得出最终的预测结果。

为便于对比分析，本文使用传统的Elman 算法、单一的LSTM 算法以及EMD-LSTM 构建模型，使用相同的数据采样点建模，对比各个模型预测结果曲线的拟合情况，并对结果进行了误差分析。针对区域能源互联网系统短期负荷序列的无规律波动特性，与EMD 相比，EEMD 能更有效地降低对预测结果的影响，EEMD-LSTM 能够更准确地对负荷进行预测。当需要预测的数据增多时，预测模型的运算时间会稍有延长。当原始数据量增大而需要预测的采样点不增加时，EEMD-LSTM 体现出了精度更高的优越性。因此，EEMD-LSTM 基本能够满足区域能源互联网短期负荷预测的要求，为能源互联网电力系统的平稳运行提供一定参考。