有限信息下基于深度学习模型的小型分布式光伏电站功率预测

甄 皓

华北电力大学经济与管理学院

0 引言

可再生能源的利用是应对中国环境和能源问题的重要措施。中国在《能源发展战略行动计划（2014-2020）》《可再生能源中长期发展规划（2007-2020）》中指出，在2020年实现非化石能源占一次能源消费比重达到15%。然而，可再生能源整合进电网的主要挑战在于可再生能源的间歇性、不稳定性。为了可靠地利用可再生能源、保障电网平衡、实时调度，不同时间范围内的可再生能源功率预测十分重要。

针对光伏功率预测，大多数文章都通过间接太阳辐照度等气象信息来预测光伏功率。一方面，全球水平辐照度预测往往与温度预测相结合，通过物理模型来预测光伏功率输出。另一方面，越来越多的学者提出了人工神经网络模型（Artificial Neural Networks, ANN）[1，2]、支持向量机（Support Vector Machine, SVM）等机器学习模型[3，4]来预测光伏电站输出。具体来讲，用于功率预测模型的输入数据往往涉及到小型气象站监测的气象数据，一般包括全球水平辐射、温度、漫射辐射水平、风速等。采用物理模型或者机器学习方法，都涉及到一段时间内当地气象数据的获取和利用。

一部分学者对有限气象信息条件下的光伏功率预测进行了研究。Cai Tao等人提出了一种神经网络预测模型，解决了无辐照量数据情况下的光伏功率预测问题[5]。Gianni Bianchini等人通过PVUSA参数模型，分别利用云量信息和光伏功率历史数据[6]、以及温度预测及光伏功率历史数据等[7]解决了无辐照量和温度信息下的光伏功率预测问题。然而，这些方法都假定可以得到有关光伏电站所在站点云覆盖指数或历史温度，对很多分布式小型光伏电站均不能适用。

在实际情况中，往往既没有准确的电站物理模型，也没有直接的太阳辐照度，或者其它气象信息（比如温度、相对湿度）的测量。基于气象数据的功率预测需要在站内安装一系列的测试设备，包括湿度、云量、雨量等传感器，建立分布式光伏电站气象数据采集系统并配备小型气象站。大型的光伏电站因规模大可以搭建气象站，成百上千个小型独立运营的分布式光伏电站，以及小型微网中的屋顶光伏电站等，往往不具备这种条件。如何在缺少气象信息的条件下，利用有限的历史数据准确预测分布式光伏电站功率具有重大的意义。

仅利用历史数据的光伏功率线性预测模型，比如：模糊理论，灰色理论，马尔可夫链（MC），自回归移动平均( Auto Regressive Moving Average，ARMA) 模型和自回归综合移动平均( Auto Regressive Integrated Moving Average，ARIMA)模型等，由于光伏出力数据的非线性，往往不能做到准确预测。计算机硬件和软件以及大数据技术的不断改进，深度学习网络已经得到关注和发展，深度学习模型具有有效提取高维复杂非线性特征的能力，并具有从输入到输出直接映射的能力。至今，人们已经提出了多种深度神经网络模型来预测光伏功率，包括循环神经网络( Recurrent Neural Network，RNN)、卷积神经网络(CNN)等。崔承刚等人[8]基于气象信息及电站信息等特征值，利用LSTM 模型对光伏电站功率进行了预测。简献忠等人[9]通过CNN-LSTM 混合模型对短期光伏电站功率输出进行预测，结论表明所提模型的性能良好。但深度学习模型进行光伏功率预测大多针对气象信息齐全的大型光伏电站，对缺乏气象信息的小型分布式光伏电站研究较少。

本文针对解决无气象站配备的小型分布式光伏电站，在无法测量气象变量（即太阳辐照度、温度、相对湿度等）的情况下，提出了一种仅基于区域内光伏电站历史功率数据的双层LSTM深度学习模型，来预测分布式光伏电站的功率。为取得最佳的预测效果，对LSTM 模型的层数及超参数对其预测效果的影响进行了分析。此外，为验证该模型的准确性，利用澳大利亚爱丽丝泉地区的分布式光伏电站的数据进行实例验证，并与使用气象数据进行预测的模型效果进行了对比。结果表明，在有限信息条件下，借助区域内光伏电站历史功率数据进行光伏功率预测的效果良好，适用于无气象站情景下的光伏功率预测。

1 基于深度学习的长短期记忆模型

长短期记忆模型（Long Short-Term Memory，LSTM）是Hochreiter＆Schmidhuber[10]提出的一种递归神经网络。它的内部存储单元和门机制克服了传统递归神经网络（RNN）训练中的梯度消失和梯度爆炸问题，将时间序列中的延迟事件保存下来，并在后续训练中进行提取，因此特别出力时间序列预测问题。为了使子模块保存长期记忆，LSTM 引进了核心结构“遗忘门”和“输入门”。遗忘门可以让循环神经网络遗忘无用的信息，输入门可以输入补充最新的记忆，两者的密切配合决定了信息的遗忘与保留。LSTM 门机制包括遗忘门、输入门、更新门和输出门。LSTM 模型的核心计算公式如下：

图1 LSTM 内部结构

基于梯度的优化算法有随机梯度下降（Stochastic Gradient Descent，SGD）、AdaGrad、RMSProp、Adam 等算法。Adam 算法是由Diederik Kingma 和Jimmy Ba 在2015 年中提出[12]，该算法是随机梯度下降算法的拓展，它能有效地基于训练数据迭代更新神经网络权重，近年来广泛应用于深度学习中，因此本文采用Adam算法。

LSTM 模型具体的构建与实现分为3个步骤。

1)获取所需数据集，对原始数据进行清洗和处理，并对训练集和验证集进行划分。

2)确定用于LSTM 模型的输入向量及输出，确定LSTM 模型的架构及具体参数，完成模型的构建。

3)利用实验数据对模型进行检验和修改，进行预测。

2 算例分析

本文为了验证所提出的模型，使用了从澳大利亚Alice Springs［51］的DKASC 的发电数据，该地区位于澳大利亚中部，南纬23°42′，东经133°52′，海拔545m。实际五个光伏系统收集的数据，五个光伏系统均采用固定式单晶硅组件[13]。五个电站每5 分钟记录一次从DKASC 收集的数据。五个电站信息如表1所示。

(1)路堤表面工后沉降曲线大致呈“勺”形，处理前，工后沉降最大值为6.7 cm，地基处理后，工后沉降值减小至2.2 cm。原因在于地基处理使地表沉降明显减小，路堤表面工后沉降也随之减小。

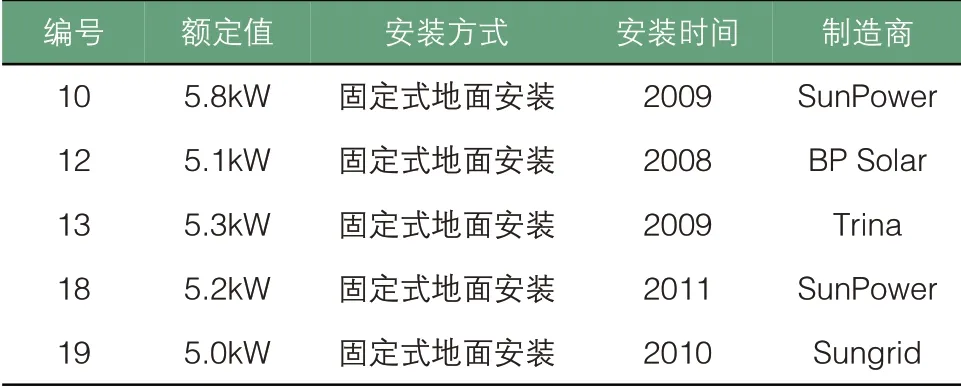
表1 五个光伏电站信息

2.1 相关性分析

如何选取合适的输入量作为光伏功率预测模型的训练数据，是建立功率预测模型的重要环节。De Giorgi 等人[14]对不同输入向量对光伏功率预测模型性能的影响进行了研究，他们设计了三种类型的向量，即向量1 包含历史PV 输出数据，向量2 包含太阳辐照度值，向量3 包含光伏组件温度。研究结果表明，三种不同向量情况下，预测误差分别为12.57%、12.60%和10.91%。Liu等人[15]对历史PV输出数据、当日天气数据、历史气溶胶指数（AI）、历史风速、天气和湿度数据等作为PV 输出预测模型的输入进行了研究，结果表明，PV输出预测模型的性能随输入变量的变化而变化。因此，合适的输入对提高光伏功率预测的准确性和模型性能，尤其在降低模型计算复杂性和计算成本方面起着至关重要的作用。如果预测模型输入的选择不当，将导致预测模型的误差增加。

光伏电站的输出功率（P）与整体水平辐射量（GHR）、水平扩散辐射（DHR）、环境温度（T）、风速（WS）和相对湿度（RH）等相关。本文对临近电站的历史输出、气象因素等分布式光伏电站的功率输出相关性进行了分析，对原始数据与各个变量之间相关性进行了直观描述，后选取2016 年一年的数据计算了各个变量（xi）与分布式光伏电站功率P之间的皮尔逊相关系数r，计算公式如下

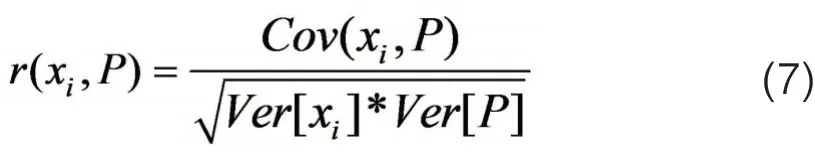
图2 变量与光伏功率输出变化

原始PV功率序列和相关的气象因素变化如图2所示，可以直观理解所选变量与光伏电站输出之间的关系。所选输入变量的范围和Pearson相关系数r如表2所示。相邻电站的历史功率数据既体现了时间和季节变化趋势，也由于处在同一地区，反映了相关气象信息的影响。根据分析可得，与10号光伏电站相关性最高的因素从高到低排序为12、13、19、18号光伏电站，整体辐射水平、漫射辐射水平、风速、温度、相对湿度，同一地区临近的光伏电站出力数据整体相关性大于气象数据的相关性。

2.2 数据处理

1）数据标准化

本文标准化采用了min-max标准化方法，它默认将每种特征的值都归一化到[0，1]之间。首先调用sklearn.preprocessing 中的MinMaxScaler 对数据进行归一化处理，将每种特征的值都归一化到[0，1]之间，其转换公式如下

2）训练测试集划分

本文对2015年1月1日到2018年12月31日4年的数据进行模型训练和验证。该数据集每5分钟一个数据点，每天288个数据点，一共420 126条数据。本文将2015 年1 月1 日至2017 年10 月20 日294 088条数据用作训练数据集，将2015年6月1日至2016 年6 月12 日126 036 条数据用作测试数据集，训练数据与测试数据之间比例为7:3。

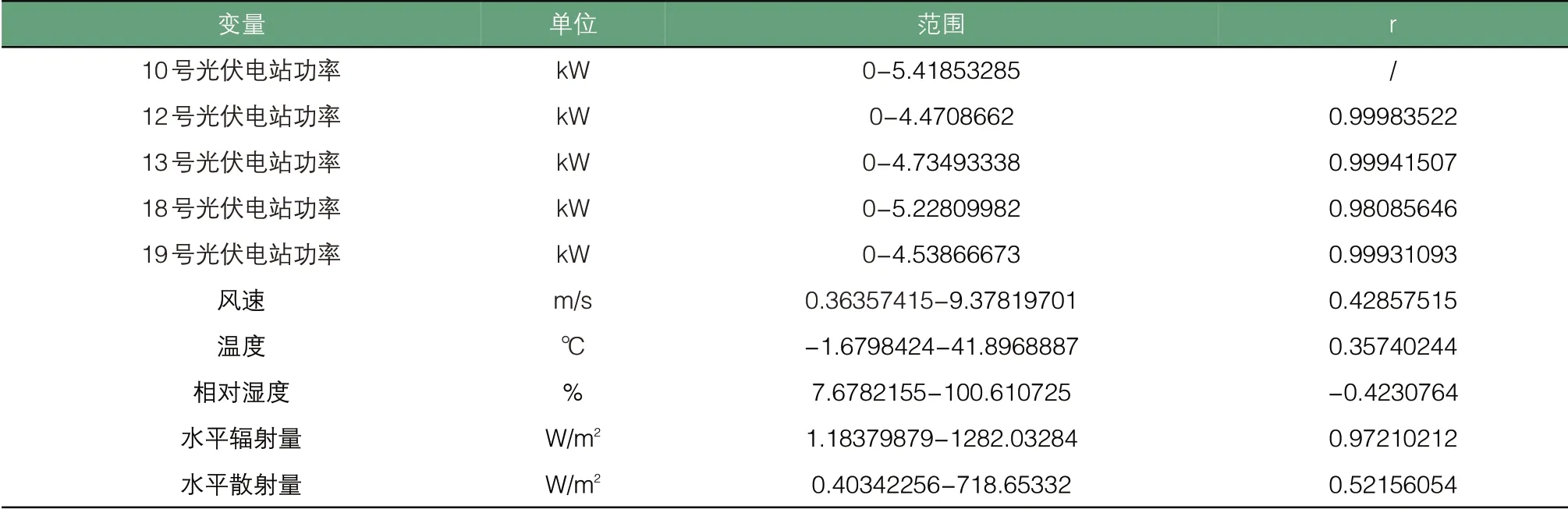
表2 变量范围以及皮尔逊相关系数

3）误差评估

本文采用均方根误差（Root Mean Square Error, RMSE）进行LSTM 预测模型性能评估[48]，评价指标的定义如下

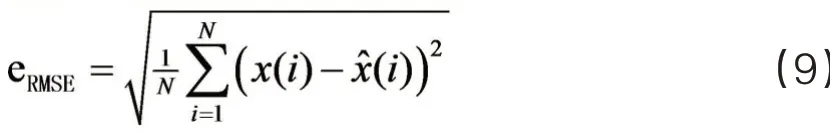
2.3 模型验证

本文结合澳大利亚Alice Springs的DKASC发电数据，应用LSTM 预测模型进行实验验证。主要包含以下内容。

1）LSTM网络层的选取及超参数影响分析

改变隐藏层层数，通过实验预测结果确定合适的网络层数。一般来讲，隐藏层越多，LSTM模型数据处理能力和学习能力越好，但神经元的增加会增加模型复杂度从而降低训练速度。首先，将LSTM模型设置不同的隐藏层层数，通过训练集对网络进行训练，用测试集进行验证得到不同隐藏层层数下网络的预测效果，如表3 所示。根据模型在不同隐藏层层数下的均方根误差，选择LSTM 网络结构隐藏层层数为两层。

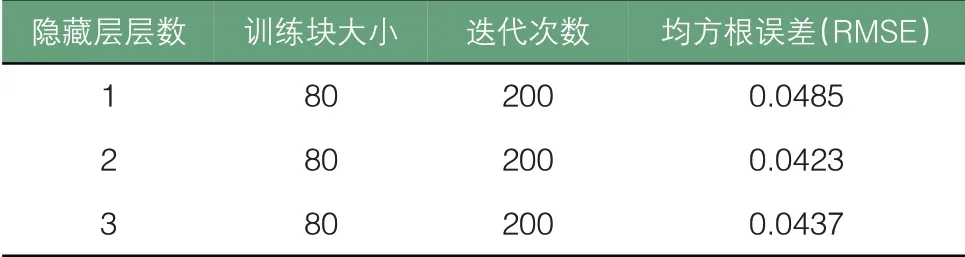
表3 不同隐藏层层数的光伏功率预测结果

选取隐藏层层数后，本文对超参数训练块大小（Batch Size）、对LSTM 模型预测效果影响进行了分析。训练块大小表示输入矩阵的大小。在神经网络训练过程中，合理范围内增大训练块大小，可以更有效地利用内存，处理数据速度也会得到提升。训练块越大，下降方向可以更加容易确定，训练震荡会稳定在合理范围内。但若盲目增大训练块大小，内存容量会被迅速占用，造成数据溢出，程序崩溃。不同训练块大小训练效果对比如表4 所示。由表4 可知，当训练块大小在80 左右时，训练效果最好。

表4 训练块大小对光伏功率预测效果影响分析

2）基于邻近电站历史数据的分布式光伏功率预测性能实证及比较

根据上文分析结果，建立双层LSTM 分布式光伏功率预测模型，第一层为4个输入单元，128个输出单元，第二层为128个输入单元，一个输出单元。训练块大小设为80，学习率通过keras 提供的回调函数学习率调节器（Learning Rate Scheduler）动态调整，步长为1，优化器采用Adam 算法。根据3.1节相关性分析结果，在缺少气象数据的条件下，选取12、13、18、19 号光伏电站的历史功率数据对10号分布式电站进行功率预测，即通过P12(t-1)、P13(t-1)、P18(t-1)、P19(t-1)来预测P12(t)。验证无大型气象站下的小型分布式光伏电站通过临近光伏电站历史数据预测功率的准确性。

此外，本文也使用LSTM 模型进行了基于气象信息的分布式光伏电站功率预测，以对比验证缺乏小型气象站的分布式光伏电站，充分利用邻近电站历史功率数据进行准确功率预测的性能。用于对比的模型输入向量包括风速（Wind Speed）、温度(Weather Temperature)、相对湿度(Weather Relative Humidity)、水平辐射量(Global Horizontal Radiation)、水平散射量(Diffuse Horizontal Radiation)五个变量。该模型也采用双层LSTM 模型，第一层为5个输入单元，128个输出单元，第二层为128个输入单元，一个输出单元，并为了更好的预测效果，在LSTM模型中引入dropout机制。

基于邻近电站历史数据的分布式光伏功率预测结果如图5 所示，基于气象信息的LSTM 分布式光伏功率预测如图6 所示，两个模型的预测效果如表5所示。根据预测结果基于气象信息的LSTM分布式光伏功率预测的均方误差为0.0477，而基于邻近电站历史数据的分布式光伏功率预测均误差为0.0439，这表明在小型分布式光伏电站缺乏气象站的条件下，通过临近光伏电站历史功率数据来预测光伏功率的均方误差更小，效果良好。

图5 基于历史数据的未来三天的光伏功率预测

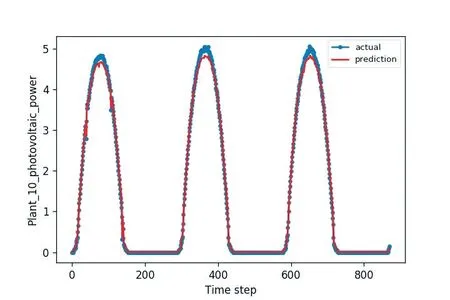
图6 基于气象信息的LSTM分布式光伏功率预测

表5 不同输入向量下的分布式光伏功率预测

3 结论

本文针对无气象站配备的小型分布式光伏电站功率预测问题，提出了一种仅基于区域内光伏电站历史功率数据的双层LSTM深度学习模型。本文通过对邻近光伏电站的历史数据、辐照度、相对湿度等变量与所研究的光伏电站功率输出进行了相关性分析，证明了相邻电站历史数据作为输入向量的合理性，通过对LSTM 模型的层数及超参数的影响分析，选取合适的层数及超参数构建了LSTM 模型。同时，为验证该模型的准确性，利用澳大利亚爱丽丝泉地区的分布式光伏电站的数据进行实例验证，并与使用气象数据进行预测的模型效果进行了对比。结果表明，在有限信息情景下，借助区域内光伏电站历史功率数据进行光伏功率预测的效果良好，均方根误差为0.0477，适用于无气象站情景下的分布式光伏功率预测。