板式表面张力贮箱导流板的理论计算与试验验证

邱中华,刘志杰,朱文杰,黄立钠,陈志坚

(1.上海空间推进研究所,上海 201112;2.上海空间发动机工程技术研究中心,上海 201112)

0 引言

表面张力贮箱依靠推进剂管理装置Propellant Manage Devices(PMD)蓄留和传输推进剂,PMD由表面张力元件组成。按工作方式,表面张力元件可以分为基于隔板形成楔角的开放式结构(包含导流板[1]、楔形海绵体[2]、贮液槽装置[3]等)和基于毛细网表面张力压差的封闭式结构(包含气泡陷阱[3-4]、启动篮[5]、复合通道[6]、筛网收集器[7]等)。板式表面张力贮箱(以下简称“板式贮箱”)的PMD构成以开放式表面张力元件为主,通常包括导流板与出口附近的蓄液器。

板式贮箱因为结构简单、零组件少、工艺性好、造价低、扩展性好等优点,在国外得到了大量应用。然而,由于地面环境不是微重力环境,板式贮箱不方便直接进行地面验证,其设计主要依赖于理论计算或仿真计算。

本文首先研究了微重力环境下导流板进行液体驱动的原理,然后据此原理进行了导流板的理论计算,之后进行了中性浮力试验,并将试验结果与理论计算的结果进行了对比。

1 导流板液体传输原理

在失重状态下,液体推进剂之间的主要作用力是分子引力,对于液位表面,则表现为表面张力。导流板就是依据导流板金属分子与液体分子的引力原理设计的。导流板是一种靠近贮箱内壁的结构,区别于传统筛网式PMD建立封闭的流动通道,导流板建立开放的流动通道,推进剂沿着通道流动。传统液体推进剂具有较好的浸润性,趋向于吸附在金属结构的夹角处,在导流板与贮箱壁交线周围形成液带。图1为沿着斜坡上导流板内液体流动的示意图[1]。

根据Laplace方程,如果Rup>Rdown,会驱动液体向下游流动,驱动压差

(1)

式中：σ为液体的表面张力系数;Rup为上游液带表面的主曲率半径;Rdown为下游液带表面的主曲率半径,另一主曲率半径均可认为是无穷大。

考虑液体沿导流板的定常流动,将导流板简化为一维流动区域,液体应满足如下的控制方程：

1)连续性方程

(2)

2)动量方程

-Adp-τwsdx-ρAadz=ρAudu

(3)

3)气液界面状态方程

(4)

式中:x为沿导流板流动的路径长度；u为液体的流动速度；A为流动截面积；Q为体积流量；p为液体的静压力；τw为液体沿壁面流动的黏性剪阻力；s为润湿周边长度；a为加速度大小；z为沿加速度方向的液位高度坐标；R为液体表面的主曲率半径(另一曲率半径为无穷大)；ρ为液体的密度。

液体沿导流板的流动一般为层流,可认为

(5)

将式(2)～式(5)进行整理可得

(6)

2 导流板液体传输能力理论计算

导流板的截面可取为很多形状,比如单竖片式、双竖片式、三折横片式、复杂式等,目前应用最为广泛的就是单竖片式[8-9],因为几种结构的液体供应能力差别不大,而单竖片式的结构最为简单,工艺性最好[10-11]。单竖片式的截面形状如图2所示。

图2 单竖片式导流板截面形状Fig.2 Simple vane cross section

根据图2可以得到s，A与R的关系,针对贮箱内导流板的设置,可以得到dz/dx的值,应用四阶Runge-Kutta法,可对式(6)进行求解。

下面使用该方法对一种经典原理型板式贮箱内的导流板[1]液体流动特性进行计算。该原理型贮箱为球柱形结构,PMD主要为导流板结构,带中心柱,贮箱形状如图3所示。贮箱的内径为φ762 mm,柱段长度为381 mm,导流板宽度为51 mm。考虑侧向加速度大小为a=0.000 5g,贮箱总流量为Q=5 ml/s,主要由侧面的一根导流板与中心柱供应,液体介质为肼推进剂,这与卫星在进行位保动作时的小推力工作状态相对应。主液池见图中左侧。因为带有中心柱结构,所以液体供应的通道可认为有2条:一条是沿图中A→B→F到达液口;另一条是沿图中A→C→D→E到达液口。

图3 原理型板式贮箱示意图Fig.3 A schematic diagram of vane type tank

计算时,取液口处E点的x坐标为xE=0,x坐标的取向沿中心柱进行,即中心柱顶端xD=1 143 mm,贮箱柱段中间部位xA=1 932 mm(381×3+381π/2+381/2=1 932),最终计算的终点F点(与E点重合)坐标为xF=2 721 mm(381×3+381π+381=2 721)。

计算结果如图4所示。图中不同的曲线代表不同的初始主曲率半径。初始的主曲率半径指流动源头(主液池)处的主曲率半径。对图3而言,即为A处的主曲率半径。

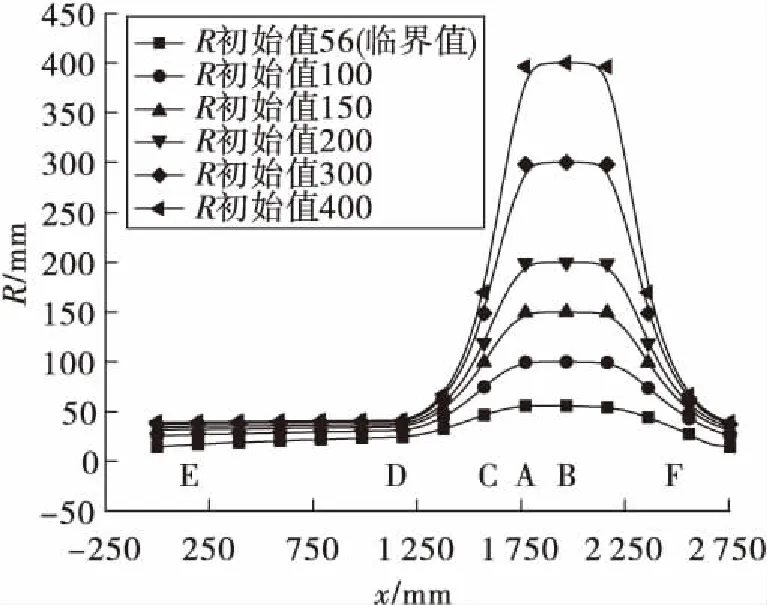
图4 原理型贮箱导流板理论计算结果 Fig.4 Theoretical calculation result of a vane ina principle vane type tank

可见,在侧向加速度的条件下,液池内液体沿2条路径流向液口时,液面处的主曲率半径均逐渐减小。随着贮箱内推进剂剩余量的减少,可以提供的初始主曲率半径减小,导致液体流通路径的主曲率半径均减小,最终达到液体供应的临界点。这与实际的液体供应情况是一致的。不同的液体剩余量对应不同的R初始值,当R初始值达到56 mm时,达到了临界供应的情况,当初始主曲率半径小于该值时,无法保证液体供应到液口处。

理论计算方法能否应用到实际的工程设计中,还要考虑理论计算方法与实际试验结果的一致性。

3 针对导流板的中性浮力试验

地面环境不是微重力环境,重力是决定液体流动的主要因素,分子引力对液体作用的影响显现不出来。因此,采用导流板结构的板式贮箱在地面进行性能试验比较困难[12]。目前常用的试验有落塔试验、抛物线飞行、空间搭载试验、中性浮力试验等[13-14]。各种方法均有其适用性与限制条件。考虑到中性浮力试验观察时间不受限制的优点,采用中性浮力试验[15-16]进行导流板在微重力条件下液体蓄留特性的试验验证。

3.1 应用于表面张力贮箱的中性浮力试验原理

中性浮力试验的基本原理是用浮力抵消重力,广泛应用于航天员微重力环境的适应性训练。

中性浮力试验设备应用于表面张力贮箱时,利用相似准则达到对微重力工况的模拟[17-18]。通常利用一种液体模拟推进剂液体,另一种液体模拟增压气体。为了模拟微重力工况,需要两种液体的密度接近,且不相溶。另外,还要考虑液体推进剂与PMD材料的浸润性,通常液体推进剂与PMD具有较好的浸润性,而增压气体与PMD不浸润[19-20]。考虑到液体密度是温度的函数,因此中性浮力试验作为表面张力贮箱模拟试验时,对温度要求较高。

中性浮力试验应用于液体微重力条件下的液位分布时,目前主要进行静平衡状态的稳态试验,需要考虑重力与表面张力的相似性,还要考虑几何相似。几何相似除了指定几何比尺外,还要考虑接触角的一致性。重力与表面张力的相似用密度差

(7)

式中l为几何尺寸。应用相似准则时,主要涉及到4种介质：实际推进剂、实际增压气体、模拟推进剂的液体及模拟增压气体的液体。

在地面环境下,a′=g,g=9.8 m/s2,根据BOND数相等,可得

(8)

如果几何尺寸没有缩比,则上式可简化为

(9)

式中：下标l为推进剂液体;下标g为增压气体;上标′为模型参数。由式(8)和式 (9)可知,模拟的微重力加速度主要取决于如下几个量：2种模拟介质的密度、推进剂的密度、模拟推进剂的液体的表面张力系数及推进剂的表面张力系数。考虑到介质参数随温度的变化,要求中性浮力试验过程中对温度的控制较为精确。实际推进剂与贮箱壁面是浸润的,实际增压气体与壁面是不浸润的,为了模拟该接触角特性,需要采用与模拟增压气体的介质不浸润的材料制作贮箱壳体。本试验用水模拟增压气体氦气,采用超薄F46贮箱壳体,用二苯甲烷模拟推进剂肼,两者的密度随温度变化关系如图5所示。

图5 两种介质的密度关系Fig.5 Density relationship of two medium

现将模拟条件设定为：推进剂肼,增压气体氦气,推进剂温度20 ℃。可得模拟的重力加速度大小与温度的对应关系如表1所示。

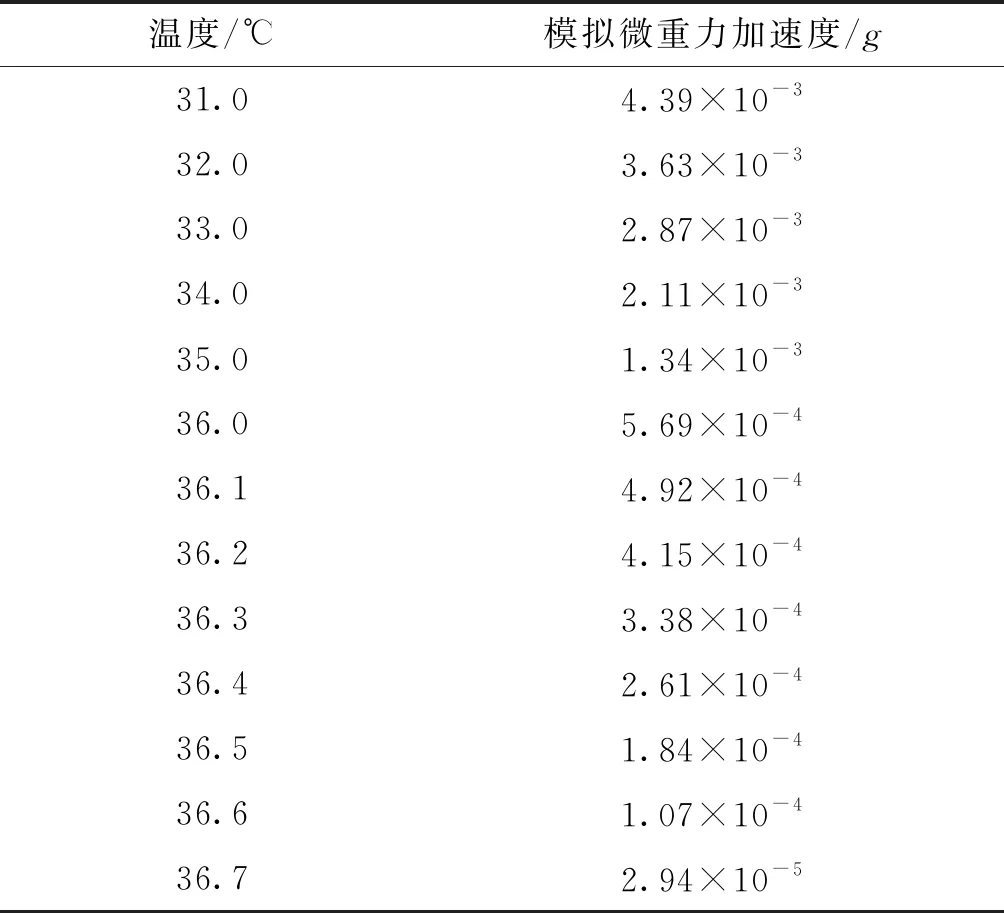
表1 模拟的加速度值与温度的关系

3.2 中性浮力试验结果

中性浮力试验用贮箱为直径φ200系列的透明贮箱,分为球形与球柱形2种,2种贮箱对应的导流板结构如图6所示。

分别进行了多种温度工况的中性浮力静平衡试验,试验结果如下所示。

图6 试验用导流板结构形式Fig.6 Vane structure for the experiment

1)球形贮箱,轴向加速度0.027 5 m/s2。

试验平衡温度33.085 ℃,不考虑几何缩比,根据式(9)计算可以得到对应的加速度值0.027 5 m/s2。试验实物如图7所示(为了便于观察,二苯甲烷添加了微量的染色剂)。

图7 中性浮力试验贮箱实物图(0.027 5 m/s2)Fig.7 The tank used in buoyancy experiment(0.027 5 m/s2)

根据液位宽度b(指在导流板外侧测量的液位横向宽度,如图8所示)的实测值与导流板高度,计算得到了对应位置(对应于计算位置坐标x处)的液位的主曲率半径R,如表2所示。

表2 试验数据表

根据已知的x坐标与主曲率半径R值,可得到R的拟合曲线,同时根据理论计算方法可以得到R的变化规律(理论计算时各量的关系如图8所示),两者的对比如图9所示。图9中给出了一种试验曲线与两种计算曲线,2种计算曲线对应不同的加速度值。

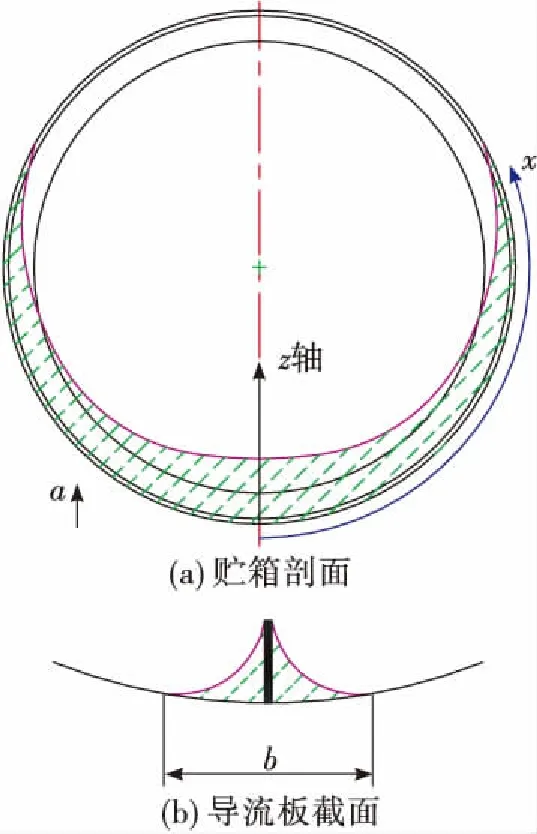
图8 理论计算各物理量关系示意图 Fig.8 The relationship of parameters for thecalculation

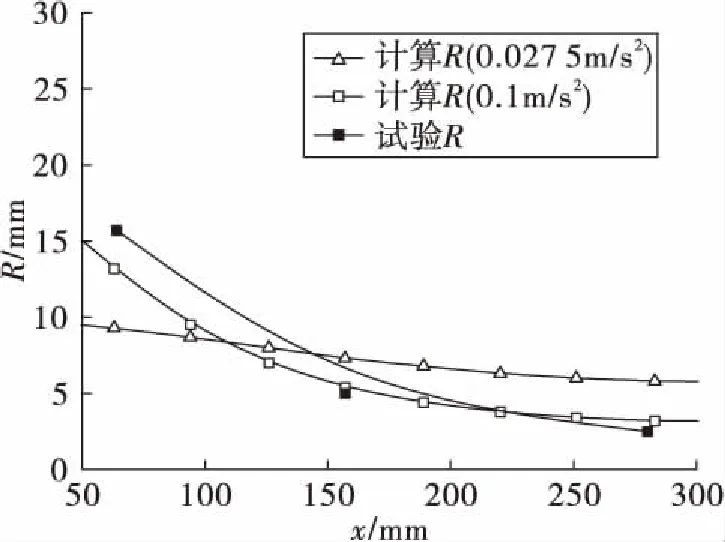
图9 试验结果与计算结果对比(0.027 5 m/s2) Fig.9 Contrast of experiment and calculationresults (0.027 5 m/s2)

2)球形贮箱,轴向加速度0.007 m/s2。

试验平衡温度35.8 ℃,根据式(9)可求得对应的加速度值0.007 m/s2。试验实物如图10所示。

试验结果与计算结果对比如图11所示。图11给出了一种试验曲线与两种计算曲线,两种计算曲线对应不同的加速度值。

图10 中性浮力试验贮箱实物图(0.007 m/s2)Fig.10 The tank used in buoyancy experiment (0.007 m/s2)

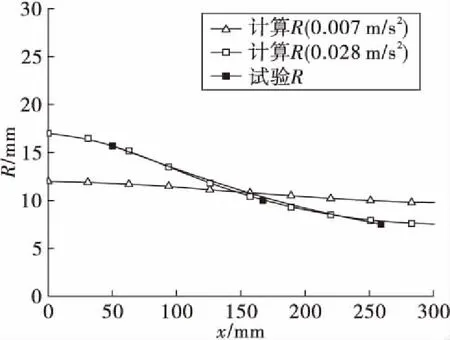
图11 试验结果与计算结果对比(0.007 m/s2) Fig.11 Contrast of experiment and calculationresults (0.007 m/s2)

3)球形贮箱,轴向加速度0.036 7 m/s2。

试验平衡温度31.855 ℃,根据式(9)可求得对应的加速度值0.036 7 m/s2。试验实物如图12所示。

图12 中性浮力试验贮箱实物图(0.036 7 m/s2)Fig.12 The tank used in buoyancy experiment (0.036 7 m/s2)

试验结果与计算结果对比如图13所示。图13给出了一种试验曲线与2种计算曲线,2种计算曲线对应不同的加速度值。

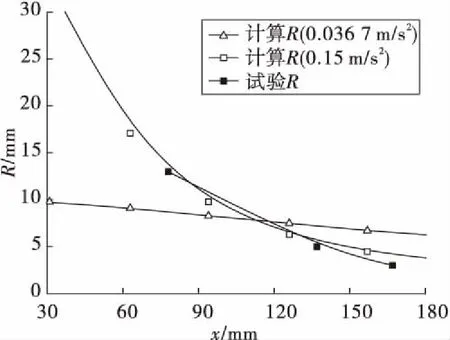
图13 试验结果与计算结果对比(0.036 7 m/s2) Fig.13 Contrast of experiment and calculationresults (0.036 7 m/s2)

4)球柱形贮箱,轴向加速度0.039 4 m/s2。

试验平衡温度31.49 ℃,根据式(9)可求得对应的加速度值0.039 4 m/s2。试验实物如图14所示。

图14 中性浮力试验贮箱实物图(0.039 4 m/s2) Fig.14 The tank used in buoyancy experiment (0.039 4 m/s2)

试验结果与计算结果对比如图15所示。图15中给出了一种试验曲线与2种计算曲线,2种计算曲线对应不同的加速度值。

5)球柱形贮箱,侧向加速度0.040 4 m/s2。

试验平衡温度31.35 ℃,根据式(9)可求得对应的加速度值0.040 4 m/s2。试验实物如图16所示。

图15 试验结果与计算结果对比(0.039 4 m/s2) Fig.15 Contrast of experiment and calculationresults (0.039 4 m/s2)

图16 中性浮力试验贮箱实物图(0.040 4 m/s2侧向)Fig.16 The tank used in buoyancy experiment (0.040 4 m/s2 lateral)

试验结果与计算结果对比如图17所示。图中给出了一种试验曲线与2种计算曲线,2种计算曲线对应不同的加速度值。

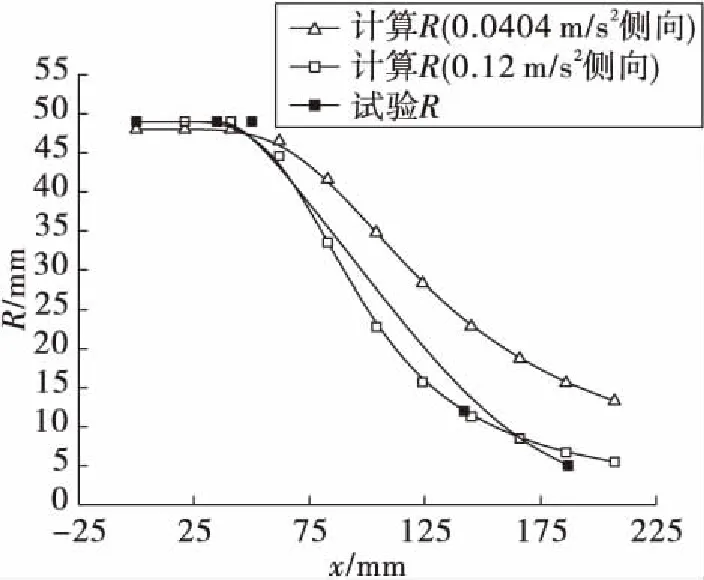
图17 试验结果与计算结果对比(0.040 4 m/s2侧向) Fig.17 Contrast of experiment and calculationresults (0.040 4 m/s2 lateral)

3.3 中性浮力试验分析

通过多种微重力工况的静平衡中性浮力试验,得到了试验曲线与计算曲线的对比关系。根据上述各条曲线的对比可以发现,中性浮力试验的结果与计算程序的结果具有一定的偏差,但对微重力加速度取一定的系数后,试验结果与计算程度结果的一致性较好。文中所列曲线的系数统计如表3所示。

表3 试验结果统计表

板式表面张力贮箱中的导流板结构通常应用于10-2～10-4m/s2微重力加速度下,而上表所列加速度已经达到了10-1m/s2,是因为本次计算针对直径200 mm的贮箱。根据相似准则,中性浮力试验基于Bond数相等,根据式(7),200 mm贮箱直径下10-1m/s2时的导流板蓄留能力相当于1 000 mm贮箱直径下4×10-3m/s2时的导流板蓄留能力。

可见,对试验结果对应的加速度取3～4倍系数后,试验结果与计算结果的一致较好。关于3～4倍系数,可以从如下2个方面理解：①理论计算有一定的简化;②中性浮力试验是相似试验,主要考虑了Bond数相似,无法考虑其它的相似条件。基于上述两方面的原因,造成了该系数的存在。

4 工程可用的导流板计算方法

本文针对板式贮箱导流板不便进行地面验证的问题,一方面建立了一种理论计算方法,另一方面利用中性浮力试验进行了地面验证。通过计算结果与试验结果的对比,发现设置一定的系数后,2种结果的一致性较好。考虑到中性浮力试验的特点,本文所述3～4倍系数是偏保守的。从工程保守的角度,可以认为,对理论加速度值取3倍系数后,可用于导流板的工程设计与计算。

基于上述认识,编制了一套适用于导流板计算的工程软件,可直接用于导流板的设计,软件界面如图18所示。

图18 软件界面Fig.18 The software interface

5 结语

1)针对板式贮箱导流板不便进行地面验证的问题,进行了理论计算研究与中性浮力试验研究,通过计算结果与试验结果的对比迭代,形成了一种经过修正的导流板液体传输能力计算方法。

2)将导流板液体传输能力计算方法进行了程序化,形成了一种工程可用的便捷的导流板计算软件。

3)通过本文研究,促进了板式表面张力贮箱设计技术的发展,加深了从业人员对于导流板性能的认识。