广义α-双链对角占优矩阵线性互补问题误差界的最优值

李 艳 艳

(文山学院 数学学院, 云南 文山 663099)

线性互补问题(Lcp(A,q))在最优停步问题、市场均衡问题、自由边界问题等力学、经济、金融等领域中都有一定的应用,详见文献[1-3].它的模型是指求x∈Rn,满足x≥0,Ax+q≥0,(Ax+q)Tx=0,其中A是实矩阵,q是实向量.

1 预备知识

定义1[9]设A=(aij)∈Rn,n,若存在α∈[0,1],使得∀i≠j(i,j∈N),有

成立,则称A是广义α-双链对角占优矩阵.

引理1[9]设A=(aij)∈Rn,n为广义α-双链对角占优矩阵,则存在正对角矩阵X=diag(x1,x2,…,xn),xi>0,使得AX是严格对角占优矩阵,并且A为H矩阵.

引理2[10]设A=(aij)∈Rn,n是H矩阵且主对角元素全为正,即存在正对角矩阵X=diag(x1,x2,…,xn)(xi>0,i∈N),使得AX是严格对角占优矩阵,则

2 证 明

定理1 设A是广义α-双链对角占优矩阵,且aii>0,对∀i∈N,令Δ-(A)≠∅,则存在正对角矩阵X=diag(x1,x2,…,xn),其中,

使得AX是严格对角占优矩阵.

证明 设

由定义知,vj>ui,则一定存在一个正数η,使得

取正对角矩阵X=diag(x1,x2,…,xn),当i∈Δ+(A)时,xi=η,当j∈Δ-(A)时,xj=1,令Q=AX=(qij),易证qii-ri(Q)>0,i∈N,所以AX是严格对角占优矩阵.

定理2 设矩阵A=(aij)∈Rn,n是广义α-双链对角占优矩阵,则存在正对角矩阵X=diag(x1,x2,…,xn),使AX是严格对角占优矩阵,其中:

且若ε>1,则

若ε<1,则

证明 由引理1知,AX是主对角元素为正的严格对角占优矩阵,对∀d∈[0,1]n,(I-D+DA)X也是主对角元素为正的严格对角占优矩阵,于是

当ε>1时,

当ε<1时,

定理证毕.

下面通过定理3和定理4对定理2做进一步详细的最优值分析.

定理3 设矩阵A,D,X为定理2所定义,

证明 令

因为f′(ε)<0,则f(ε)在区间上是单调递减函数,故

因为f′(ε)>0,f(ε)在区间上是单调递增函数,故

定理证毕.

定理4 设矩阵A,D,X为定理1所定义,

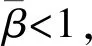
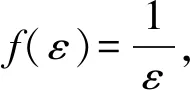
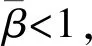
因为f′(ε)>0,f(ε)在区间上是单调递增函数, 故

定理证毕.

3 结 论

本文得到了H矩阵的新子类广义α-双链对角占优矩阵线性互补问题的误差界,并通过对函数单调性的详细分析,得到了该类矩阵误差界的最优值.该最优值的最大优点是只与矩阵元素有关,便于计算.