基于Bessel-Legendre不等式的连续广义时滞系统容许性条件
于姗姗, 孙 欣
(沈阳师范大学 数学与系统科学学院, 辽宁 沈阳 110034)
广义系统,又称奇异系统、广义状态空间、微分代数系统或半状态系统等.广义系统是一类比正常系统更具广泛形式的动力系统,广义系统在航天工程、电路网络、网络控制、电力系统和无损传输线等领域有着广泛的应用[1-11].在许多动态系统中,时滞的存在往往会导致系统性能变差、振荡甚至不稳定. 对时滞系统稳定性的研究引起了众多学者的广泛关注,并取得大量研究成果.
近年来,很多学者研究了广义时滞系统的容许性问题. 一般地,广义时滞系统的容许性分析都是以充分性条件形式给出. 根据容许性条件是否依赖于时滞,又分为时滞依赖型和时滞独立型容许性条件. 对于时滞依赖型的容许性条件,系统所允许的时滞越大,条件的保守性就越小.针对广义时滞系统容许性问题,构造一个合适的Lyapunov-Krasovskii泛函(简称L-K泛函)对于推导更小的保守性条件尤为重要,人们在构造L-K泛函上做了很多工作. 如采用参数化L-K泛函[2]、增广的L-K泛函[3-5]和引入三重积分项[3-4]等.
另一方面,能否获得更小保守性的容许性条件与怎样处理L-K泛函中求导后的积分项密切相关.在处理L-K泛函中求导后的积分项上,积分不等式被广泛应用于时滞系统[12-16],通过积分不等式对L-K泛函中求导后的积分项的处理,可以方便地将L-K泛函求导后的积分项转化为线性矩阵不等式(简称LMI),并用MATLAB中LMI工具箱求解.例如,Jensen不等式[12]和Wirtinger不等式[13]被用来处理L-K泛函求导后的积分项. 此外,Jensen不等式和Wirtinger不等式也被应用于广义时滞系统的容许性分析[4-5].
文献[14-15]中提出Bessel-Legendre不等式(简称B-L不等式),B-L不等式相比Jensen不等式和Wirtinger不等式对积分项的放大程度更小,更接近被放大积分项的真值,具体说明可见文献[15].B-L不等式被用于时滞系统[16]. 然而,如果将B-L不等式应用连续广义时滞系统,最后容许性条件难以表示成可解的LMI形式,所以对于广义时滞系统,并没有发现B-L不等式的应用.
本文针对连续广义时滞系统,建立了一个新构造的增广的L-K泛函并结合B-L不等式,获得以LMI形式表示的保守性更小的容许性条件.通过数值算例说明所用方法的有效性.
Rn表示n维欧几里得空间;Rm×n代表m×n实矩阵;X>0(或X≥0)表示X是正定(或半正定)矩阵,X>Y(或X≥Y)表示X-Y是正定(或半正定)矩阵;‖x‖表示向量x的欧几里得范数;I代表适维的单位矩阵;缩写diag{…}代表块对角矩阵;上标“T”代表矩阵的转置;符号“*”表示矩阵中的对称项;sym{Z}代表Z+ZT是矩阵Z与矩阵Z转置之和.
1 问题描述
考虑如下连续广义时滞系统:
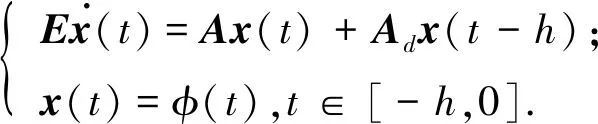
(1)
其中,x(t)∈Rn为系统状态向量,Rn是定义在实数域上的n维向量空间,参数h>0表示定常时滞,φ(t)∈R是连续的向量值初始函数. 矩阵E∈Rn×n且rank(E)=r≤n.A,Ad为已知适当维数的常数矩阵.
定义1[1]若det(sE-A)≠0,则称矩阵对(E,A)是正则的;若deg(det(sE-A))=rank(E),则称矩阵对(E,A)是无脉冲的;若det(sE-A)=0的根全部具有负实部,则称矩阵对(E,A)是稳定的;若矩阵对(E,A)是正则,无脉冲,稳定的, 则称为容许的.
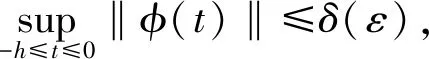
引理1[15](三阶B-L不等式)对于矩阵W∈Rn×n,W>0,参数b>a,向量函数x:[a,b]→Rn, 则以下不等式成立:
其中
引理2[15](四阶B-L积分不等式)对于矩阵W∈Rn×n,W>0,参数b>a,向量函数x:[a,b]→Rn,则以下积分不等式成立:
其中,
2 主要结果
定理1 对于给定的参数h>0,连续广义时滞系统(1)是容许的. 若存在正定矩阵,P=(Pij)∈R5n×5n(i,j=1,2,…,5.),Pij∈Rn×n,正定矩阵Q,W,S和任意矩阵Z,L∈Rn×(n-r)为列满秩常数矩阵,且ETL=0,满足下面线性矩阵不等式:
其中:
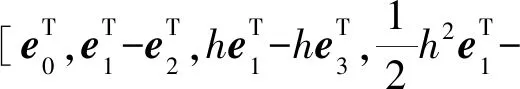
Γ3=-he3+2he4;
Γ4=he3-6he4+12he5;
证明 证明分为2部分,先证明正则性,无脉冲性;再证明稳定性.首先证明系统(1)是正则,无脉冲的.式(2)可以写成
Φ=Φ1+Φ2<0.
(3)
其中:
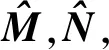
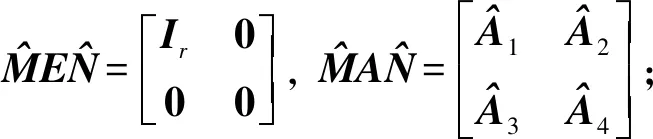
(5)
(6)
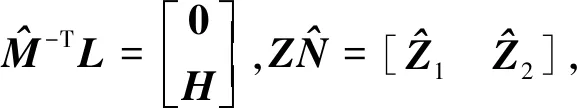
(7)
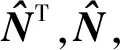
则有
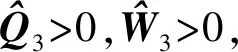

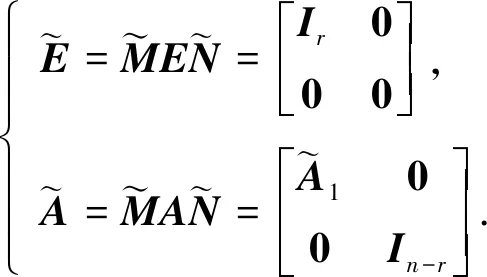
(8)
定义
又
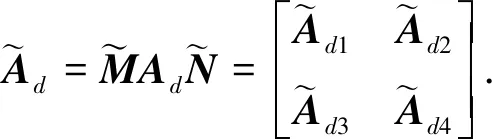
(11)

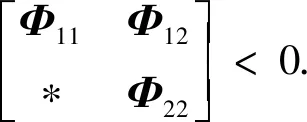
(12)
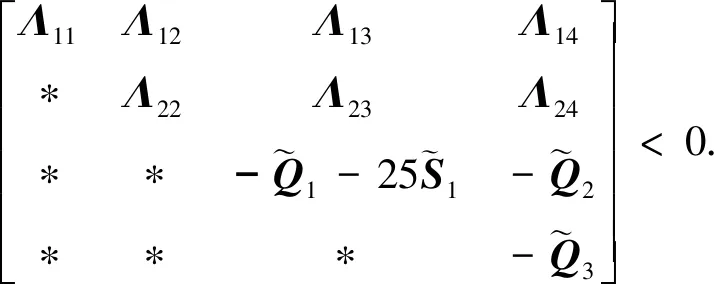
(13)
其中:
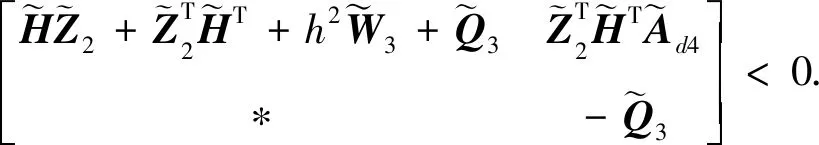
(14)

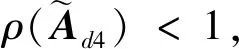
(15)
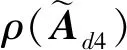
利用式(8)和式(11),系统(1)可以写成
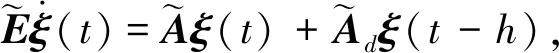
(16)
即
其中:
由奇异系统受限等价变换可知,系统(1)与系统(16)在稳定性上是等价的. 为系统(16)选择如下形式的L-K泛函:
其中:
沿着系统(16)关于t对V(ξ(t))求导数,得
(21)
从而
从而
(22)
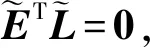
(23)
由式(17),式(18)和式(21)~式(23),整理得
其中:
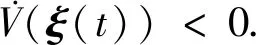
利用式(15),下面的证明步骤类似于文献[7]中引理2.2和文献[6]中定理1,可得出系统(1)是稳定的,因此系统(1)是容许的. 证毕.
注释1 通过引入积分项
将η(t)增维,得到增广的L-K泛函V1(ξ(t)),这样更有利于使用三阶B-L不等式及四阶B-L积分不等式.否则,直接应用B-L不等式可能造成LMI无解.
注释2 利用保守性较小的三阶B-L不等式及四阶B-L积分不等式处理泛函求导后的积分项,得到了连续广义时滞系统容许性条件. 正是由于利用了这些新技术,本文得到的容许性条件比现有文献中的结果具有更小的保守性.
3 数值算例
例1 考虑如下连续广义时滞系统[2]:
其中c为参数,通过MATLAB的LMI工具箱求解,表1分别列出文献[2,8-9,4-5]及定理1算出系统允许最大时滞hmax. 说明本文所用的方法具有更小的保守性.

表1 系统允许最大时滞hmaxTable 1 The maximal allowable delays hmax for system
注: N为时滞分割的区间数目.
4 结 论
本文研究了连续广义时滞系统的容许性条件.通过构造新的含有增广向量的L-K泛函,结合保守性较低的B-L不等式处理技巧,得到新的连续广义时滞系统的容许性条件.最后,通过MATLAB中LMI工具箱求解,对数值例子进行计算,与现有结果进行比较,说明了本文采用方法的有效性和优越性.

