抓毛织物表面质量的视觉检测方法

魏哲 李安然 罗文量 付子强 李博 王旭

摘 要：针对抓毛织物表面质量的量化检测问题，提出一种基于计算机视觉的抓毛织物表面质量检测方法。采用切向背光法获取抓毛织物的轮廓图像，根据绒毛区域的灰度直方图特征，对绒毛区域进行分割，再利用形态学算法对绒毛区域内出现的空洞进行填充，从而得到完整的绒毛区域。通過Freeman编码提取绒毛区域的两侧边缘坐标，利用最小二乘算法拟合绒毛下边缘得到绒毛厚度基准线并建立绒毛厚度模型。同时采用统计直方图构建绒毛分布状态参数模型。结果表明：该方法对织物的颜色、底布的纹理不敏感，可以实现对抓毛织物表面质量进行综合量化评定。

关键词：抓毛织物;视觉检测;最小二乘拟合;统计直方图

Abstract：Aiming at the problem of quantitative detection of surface quality of fluff fabric， a method based on computer vision for detecting the surface quality of fluff fabric was proposed. The tangential backlight method was used to obtain the contour image of the fluff fabric. According to the gray histogram feature of the fluff region， the fluff region was segmented， and then the morphological algorithm was used to fill the voids in the fluff region. Thus， a complete Fluff area was obtained. The edge coordinates of the two sides of the fluff region were extracted by Freeman coding， and the lower edge of the fluff was fitted by the least squares algorithm to obtain the fluff thickness reference line. As well， the fluff thickness model was established. At the same time， the statistical histogram was adopted to construct the parameter model of fluff distribution state. The experimental results show that the method is not sensitive to the color of the fabric and the texture of the base fabric， and the surface quality of the fluff fabric can be comprehensively evaluated by this method.

Key words：fluff fabric; visual inspection; least square fitting; statistical histogram

抓毛工艺是织物的后整理工序，包裹有针布的辊子在锡林上呈圆周分布，织物紧贴在辊子表面，二者之间产生相对运动，同时辊子既有自转又绕着锡林进行公转，在织物的表面形成柔软、致密的绒毛[1]。织物抓毛工艺是一个动态的物理变化过程，针布上针的状态、织物的张力、辊子的转速等工艺参数都将影响到抓毛产品的风格和质量[2-4]。目前，对织物表面的绒毛状态检测主要采用人为经验的主观评判，该方法检测效率低，且检测结果容易受到外界因素的影响。

随着机器视觉技术、信息技术、人工智能等在纺织服装领域应用的深入开展，基于机器视觉的织物表面质量检测已成为质检的重要方向。织物疵点的识别与分类中，通过视觉系统获取织物表面信息，采用结构方法、统计学方法、频谱分析方法、深度学习等提取织物疵点典型特征，构建织物疵点数据库，实现了典型疵点的识别与分类，提高了白坯布等织物表面疵点智能化识别分类[5-8]。织物表面的起毛起球量化测量中，在分析了起毛起球成因的基础上，通过在空间域、频域的变换对各种原因的起毛起球进行图像预处理、分割、特征提取，构建神经网络等识别与分类模型，对起毛起球进行等级评估[9-12]。杨松林等[13]对牛仔布表面绒毛采用0.7～4.5倍放大镜头的视觉系统采集图像，通过建立牛仔布表面绒毛率的数学模型，对采样宽度为2～10 mm内的牛仔布表面绒毛率进行测量。该方法的采样长度较小，不能全面反映整幅牛仔布表面的绒毛状态。

为了对抓毛工艺后的织物表面绒毛质量进行量化、客观评定，实现自动化检测，本文提出了面向抓毛工艺织物表面绒毛质量评定的视觉检测方法。通过对抓毛织物表面绒毛轮廓图像提取出绒毛区域的边缘特征，构建表征绒毛质量评定的绒毛厚度和绒毛分布程度两个量化评定参数模型，实现绒毛质量 的量化及客观评定。

1 织物表面绒毛图像的边缘特征提取

1.1 绒毛轮廓图像的获取

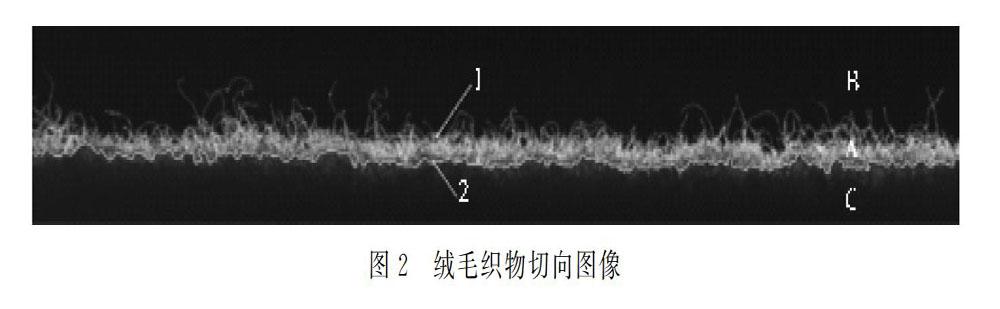
如图1所示，相机1的光轴Z与辊子4的轴向外轮廓（虚线除）相切，被测织物随传送装置运动，当运动到拍摄位置（虚线处）时，得到的绒毛轮廓图像如图2所示。

由图2可知，图2中A区域为织物表面由抓毛工艺形成的绒毛区域，B和C区域为背景区域和织物底布区域。

1.2 绒毛区域的边缘特征提取

绒毛区域从织物底布开始到绒毛顶端为止，该区域是检测抓毛工艺质量评定的部分。对绒毛图像进行预处理，增强绒毛区域的对比度，突出绒毛区域的特征，提高图像的质量。根据绒毛图像的灰度直方图分布具有峰谷的特征，对绒毛区域进行最大类间方差法的分割处理。二值化后的绒毛区域还存在空洞和断点区域，对此采用形态学开闭运算进行填充[14-15]，得到完整的绒毛区域如图3所示。

绒毛区域的边缘是绒毛区域与背景区域和织物底布区域的分界，为了评定绒毛质量，本文采用Freeman编码提取绒毛区域的边缘特征，其计算过程为：

a）将图像轮廓边缘标记为M×N，并生成（M+2，N+2）的0矩阵，用以包围边缘轮廓，形成8邻域图像;

b）寻找第一个像素为1的坐标，建立首个搜索方向的起点，然后对其余7个方向进行搜索，寻找下一个像素为1的坐标，全局搜索，并记录当前的坐标;

c）当其余7个方向均为0时，则停止计算，并返回坐标值。

通过Freeman编码算法提取绒毛区域的边缘特征如图2中曲线1和曲线2所示，边缘曲线1为织物底布与绒毛区域之间的边缘，边缘曲线2为绒毛区域与背景之间的边缘，所提取的绒毛区域边缘与实际绒毛区域基本相吻合。

2 绒毛质量评定参数模型

抓毛工艺生成的绒毛密实，表面整齐，为了对绒毛表面质量进行量化，本研究将图2中的绒毛区域边缘轮廓曲线由图像坐标变换到如图4所示的直角坐标中。在直角坐标中建立绒毛厚度参数模型和绒毛分布状态参数模型，对绒毛表面质量进行量化来综合评定。

2.1 绒毛厚度参数模型

绒毛與织物相连接的边缘是绒毛区域开始的地方，通过将绒毛与底布的边缘f（x）进行最小二乘法拟合后，将这条拟合线作为评定绒毛厚度的基准线。设图像坐标系为xoy，采用最小二乘法对厚度基准进行拟合[16]得到厚度基准线方程为：

根据绒毛区域与织物底布边缘拟合得到的厚度基准线如图4中的点划线所示。绒毛厚度可定义为绒毛上边缘轮廓g（x）上各点到最小二乘拟合的基准线距离的绝对值的平均值，其表达式（2）为：

由式（2）可知，ra越大则抓毛生成的绒毛厚度越厚，反之则越薄。

2.2 绒毛分布状态参数模型

绒毛在水平方向的分布状态为绒毛区域与背景的边缘为绒毛上边缘轮廓g（x）的分布特征，表征了绒毛表面的分布情况。以绒毛轮廓g（x）的最小二乘中线为基准线，绒毛上边缘轮廓各点接近基准线的点数越多，则绒毛分布越均匀;反之分布程度越差。以基准线为零点，将绒毛上边缘轮廓上接近基准线的点数的概率定义为绒毛分布的程度，其表达式（3）为：

式中：n为绒毛轮廓点的上限，g（n）表示范围内的灰度总点数，S（k）表示值为k的点数。

采用统计直方图对靠近原点的绒毛轮廓分布概率进行统计，定量地分析绒毛分布程度。图4中绒毛轮廓曲线的统计直方图如图5所示，靠近拟合中线的点数最为集中，其概率最高，则表征绒毛分布程度较好，分布较为均匀。

3 数据分析

3.1 试验参数

为了验证本文方法的精度和稳定性，采用如图6所示的3种不同颜色、不同织物底布的抓毛织物进行试验。

在图1的检测系统中进行试验，系统的织物传送速度控制在0～50 m/min，绒毛织物图像采集装置为分辨率1 024×1 024、帧率59 fps的AVT GE1050工业相机;根据视场配置f=8 mm的Computar镜头，带磨砂散射的条形LED的光源提供稳定照度。相机安装的物距为300 mm，采集绒毛织物的幅宽范围为500～800 mm，视觉系统的标定参数为K=0.358 mm/pixel。

3.2 织物轮廓边缘提取

在织物运动速度为20 m/min，采样幅宽为500 mm，通过本文轮廓边缘提取算法得到在直角坐标中的绒毛区域边缘轮廓曲线如图7所示，图7中曲线反映了绒毛区域在厚度和水平方向的分布状态。

3.3 绒毛质量评定参数分析

3.3.1 厚度参数分析

对绒毛区域与织物底布边缘建立厚度参数的基准中线，如图7中的虚线所示，通过式（2）得到的绒毛区域厚度平均值及最大厚度值如表1所示。

由表1可知，平均厚度能够反映出绒毛织物在厚度方向的状态，最大高度体现了绒毛自然状态下的长度状态，但是这两个参数不能客观表达水平方向的分布状态。

3.3.2 绒毛分布状态参数分析

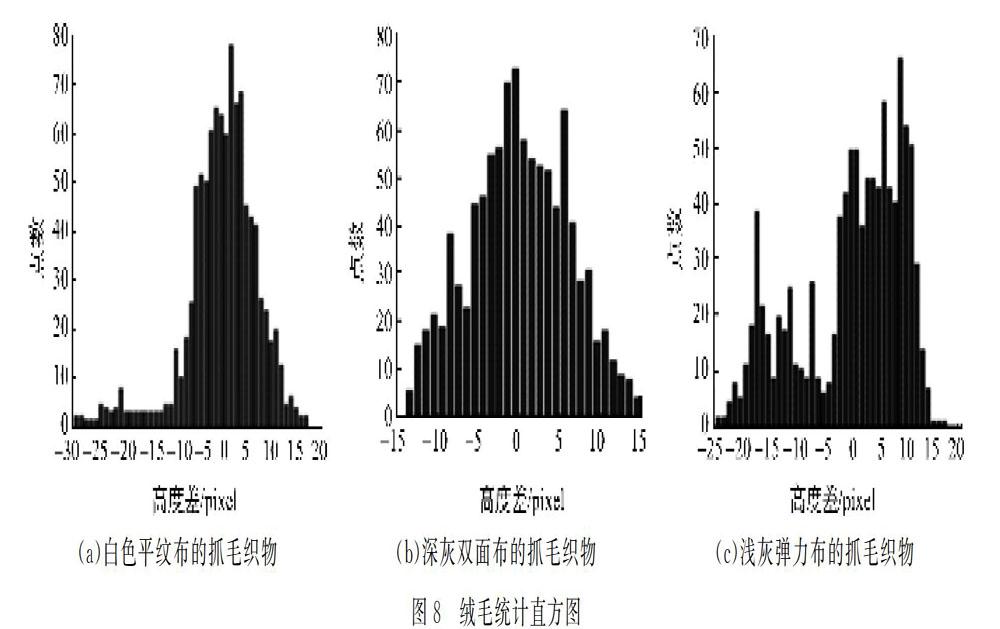
为了综合评定绒毛织物表面状态，还需考虑绒毛在水平方向上的分布状态，对3组织物的绒毛轮廓采用统计直方图进行概率统计，其结果如图8所示，绒毛分布状态如表1所示。

由图8可知，图8（a）和图8（b）中靠近原点的概率最高，其曲线变化小，分布较为均匀;图8（c）中靠近原点的概率最低，其曲线变化大，分布状态较差。从统计直方图能够比较形象地反映出绒毛轮廓在水平方向的状态。通过统计直方图可以对平均厚度接近的绒毛表面进行综合量化评定。

综合利用绒毛平均厚度、最大厚度和绒毛分布状态等参数对抓毛织物表面质量进行量化评定，评定参数对于织物颜色不敏感，织物底布的不同类型对评定结果影响较小。

4 结 论

a） 构建了视觉检测系统的试验平台，开发了抓毛织物表面质量的视觉检测算法，具有客观、量化、准确的对抓毛织物质量进行评定。

b）采用切向背光法的成像原理获取绒毛轮廓图像，以最大类间方差法有效地分割出绒毛区域，在此基础上采用Freeman编码提取绒毛区域的两侧边缘特征。

c） 建立了评定绒毛质量的厚度参数模型和绒毛分布状态参数模型，分别在厚度方向和水平方向综合评定绒毛质量。在构建的试验平台中对3种不同颜色和底布的抓毛织物进行了方法的验证，结果表明，本文方法可以有效地对抓毛织物表面质量进行综合的量化评定。

参考文献：

[1] 孙菲菲，徐平华，丁雪梅.服装风格客观评价的研究现状与不足[J].上海纺织科技，2017，45（10）：1-4.

[2] 陈慧.毛纺面料特性对服装设计的影响[J].毛纺科技，2016（8）：48-50.

[3] MAK K L， PENG P， YIU K F C. Fabric defect detection using multi-level tuned-matched Gabor filter[J]. Journal of Industrial and Management Optimization，2012，8（2）：325-341.

[4] JING J F. ZHANG H H， LI P F， et al. Fabric defect detection using Gabor filters and defect classification based on LBP and Tamura method[J]. Journal of the Textile Institute， 2013，104（1）：18-27.

[5] 李春雷，高广帅，刘洲峰，等.应用方向梯度直方图和低秩分解的织物疵点检测算法[J].纺织学报，2017，38（3）：149-154.

[6] 杨曼，李仁忠，刘阳阳，等.基于改进迭代匹配滤波的织物疵点检测[J].西安工程大学学报，2017，31（3）：383-389.

[7] 何峰，周亚同，赵翔宇，等.纹理织物疵点窗口跳步形态学法检测[J].纺织学报，2017，38（10）：124-131.

[8] KIM S M， PPAR CK. Evaluation of fabric pilling using hybrid imaging methods[J]. Fibers and Polymers， 2006，7（1）：71-89.

[9] 宋玉玲，孙淑娟，杜平凡，等.针织用腈纶仿羊绒纱的抗起毛起球性[J].现代纺织技术，2018，26（6）：39-42..

[10] 周圆圆，潘如如，高卫东，等.基于标准样照与图像分析的织物起毛起球评等方法[J].纺织学报，2010，31（10）：29-33.

[11] 马浩，景军锋，李鹏飞.基于机器视觉的管纱毛羽检测[J].西安工程大学学报，2017，31（3）：377-382.

[12] 张婉婉，景军锋，苏泽斌，等.纱线条干均匀度检测算法研究[J].西安工程大学学报，2017，31（1）：58-64.

[13] 杨松林，马帅，丁朝鹏，等. 应用机器视觉的织物表面绒毛率测试系统[J]. 纺织学报，2017，38（6）：118-123.

[14] 何立风，刘艳玲，钟岩，等.一种高效的视频背景提取方法[J].微电子学与计算机，2019，36（2）：57-61，67.

[15] SELVER M A， AVAR V， ZDEMIR H. Textural fabric defect detection using statistical texture transformations and gradient search[J]. Journal of the Textile Institute Proceedings & Abstracts， 2014， 105（9）：998-1007.

[16] 尤中桐，王太勇，劉清建，等.一种基于最小二乘法的离散点螺旋线式拟合算法[J].中国机械工程，2018，29（20）：2502-2506，2514.