发展直观思维 解决数学问题

张永国 张建芬

(1.邢台学院，河北 邢台 054000；2.邢台第七中学，河北 邢台 054000)

0 引言

数学作为一门自然科学，其产生和发展与“问题”有着千丝万缕的联系，也是科学构成的坚实基石。问题是数学的核心，发现问题是学习数学的基本，选择合适的方法分析问题是判定数学学习有效性的途径，而最终解决问题是数学学习的根本。数学学习的过程，就是这样认知的一个过程。根据学生年龄和思维水平的特点，选择适当的数学方法，可以帮助学生巩固、拓展知识和技能，发展实践能力，激发学生的探究和创新精神，为终身学习和工作，奠定良好的基础。选择怎样的方法，怎么推进方法的进行，所选方法有何意义，是本文研究的重点。

1 直观思维的理论和意义

在实际的数学教学中，围绕“问题解决”的理念，逐步开展卓有成效的实践。1988年第六届国际数学教育会议上，问题解决被正式列为大会的研究课题之一，并将提出问题解决、模型化及应用，列为学生数学课程的一部分。提高学生问题解决的能力，逐渐成为本国数学教育的目标之一，也成为世界各国数学教育的热点问题之一。直观和直观思维是解决数学问题的一种有效方法，已经被很多学者所证实。

1.1 直观思维的内涵及意义

直觉没有固定的概念，一般分为预期性直觉和确定性直觉。预期性直觉已经被心理学家所研究，0.Selz (1922)已经用到了预期直觉这个词语，Bruner (1965，p.55-68)和 Wescott (1968)也用到了直觉和直觉思维。应用直觉词语时，经常理解为“直觉理解、直觉解释、直觉现象”。直觉是一种心理现象，是指在没有任何推论或感觉经验的情况下获得知识的能力。从数学教育的观点来看有多种见解，其一认为不进行直观思维分析、比较、综合等逻辑手段，而直接结论的思考方式。另外，直观的思考是没有形式上的证明和类似外部正当化要求，而是直接被接受的认知形态。

1.2 直观思维在数学教育中的影响

Hersh(1998，p.61)认为，数学实践中，直觉无处不在。Raymond Wilder (1984).没有直觉,数学没有创造性,但直觉依赖于知识组成的增长。

数学思维存在着诸如公理、定义、证明等类似形式的逻辑性思维，还有一般化、抽象化、类推、归纳等非形式性的直观性思维。数学的思维活动，认识数学的事实是直观的，最后是逻辑思维起作用，这个过程是螺旋式的。

直观和逻辑尽管有形式上的区分，但在解决问题的过程中，却发挥着互补的作用。Poincaré(1905)说：“逻辑科学不是唯一的科学，逻辑上不充分的，还要有直觉补充和解读的作用”。

2 运用直观思维，解决数学问题

2.1 课堂教学，提示引导

讲授式是课堂中普遍使用的一种教学方法，可以使学生准确、系统地掌握教学内容，但又限制了学生主动性作用的发挥和学生思维能力的发展。教育工作者一直积极提倡自主发现问题、合作分析问题、探究解决问题的学习模式，并注重学生思维能力，特别是直观思维能力的培养。在数学问题中，类似一些函数的极值问题，不等式中的不等关系，还有空间模型的转化问题等。

例1f(x)=x2+ax+b在[0，1]的最大值为M，最小值为N，求M-N的值(与a,b的关系)。

从函数的最值求法来看，需要分析a,b值和0,1的关系，然后分情况讨论求值，过程很复杂。如果在课堂上引导学生直观观察函数值的变化与a,b的关系可知，a影响函数图像的左右平移，b影响函数图像的上下平移，也就是函数值的大小，而最值的差应与a有关，与b无关。本题也可通过观察引入特殊值验证。

2.2 以直观思维为手段，发展多种思维方法

分析数学问题的过程中，整体思想是一种重要的方法，学生通过直观思维方法，把握问题的组成和结构，揭示问题的内在本质。课堂教学，解决数学问题时，教师要引导学生宏观上把握，细节上分析，始终以问题的基本框架为中心，用直观思维的方法去培养整体的思路和方法。

数学问题中，数形结合思想贯穿始终，且能很好地发挥互补作用。数形结合可以使问题形象化，运用联想、推理等手段，引导学生的直观思维的开发，且直观思维也加深了学生对数形结合思想的认识。

数学问题来源于生活，在课堂教学活动中，教师可以把数学问题和生活实际联系起来，通过直观的观察，合理的想象，构建概念的基本模型，同时又可以加深概念的深层次理解。

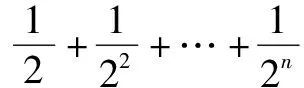
这是初中的一道习题，如果放到高中等比数列求和中，一目了然，通过等比数列求和公式可得，但在初中数学中如何解决呢？可通过直观观察，借助数形结合完成求值。

直观思维与数形结合，完美解决了一类数学问题，既高效又准确。

2.3 直观性思维，是模型的构造为内在基础

直观思维最重要的特征，是不经逻辑推理，可以确立结论。所以在培养直观思维的过程中，根据问题的特征可以建立模型思想，比如函数模型、三角函数模型、方程模型、不等式模型等，提高问题解决的效率。

例3 证明不等式lnx0)。

分析：此不等式的证明可以直观考虑函数图形之间的关系。从问题形式来看，可构造函数模型，利用函数导数的性质(函数一阶导数的增减性)求出不等关系。

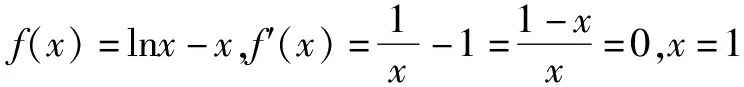
3 如何培养直观思维，解决数学问题

3.1 发展图式思维，有效解决问题

思维是人脑借助语言对事物的概括和间接的过程，用来探索与发现事物的内部本质联系和规律性。而图式，作为一种直观的思维方式，在处理问题的过程中，发挥着重大作用。哲学家和心理学家认为，图式是一种用来感知世界的事物，是一种天生的逻辑思维方式和行为模式。康德用图式来描述物体的概念，解释真实世界中对象与理解之间的联系。Rumelhart(1980年)，把图式描述为“认知的积木”。Rumelhart和Norman(1985年)的特点如下：

(1)图式有变量的。

(2)图式可以被嵌入。

(3)图式表现在各个层次的知识范畴。

(4)图式代表知识而非定义。

(5)图式是一种主动识别功能，目的在于处理的数据并评估。

数学问题的基本运算模式是加减乘除，图式可以根据其特点巧妙地处理一些复杂的问题。Nesher和Hershkovitz(1994)发现所有的问题都可以通过以下3种基本模式解决。

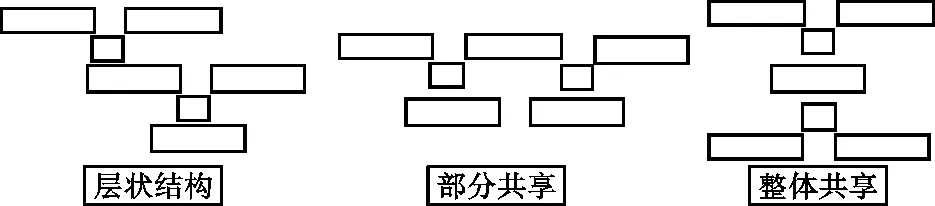
图1 3种基本模式解决

用这种图式分析，解决问题的方法，可以有效解决不同难度的数学问题，对培养学生的直观思维能力，有很大的帮助。同时也发现用这种方法解决问题比普通的解决方法更有效，详见Hershkovitz(1996)和Nesher(1998)。当然也可把这3种模式推广到多层级形式。

3.2 根据不同的发展阶段，选择合适的教学方式

小学阶段的数学中,建立与学生初级直觉联系，有2种方法：首先,应鼓励学生用自己的方式发现数学程序的过程,而不是由教师的直接教授，这应是最有效的解决方案。这种方法可用于学习形式数学算法,如增加分数和乘法数字；还可用于较少算法问题的求解情境,如程序过程的发现,数值的相对大小(偶)数的相对大小的确定。第二,可以重新设计学校的教学,以便通过使用教学工具来促进知识的联系，允许学生把数学的抽象概念和数字化的抽象概念具体化,并以此为基础,建立抽象数学基础。

在中学阶段，这2种教育策略(即发现学习和使用手法)似乎更难实形成自我生成数学的过程和规则，因为出现复杂的符号和方程式，而这些符号对于学习更高级的代数更有用。因而在学习过程中，要遵循循序渐进的过程，发现数学方法的价值不在于知识本身，而是形成思维的过程。

总之，在实际的数学学习中，直觉和洞察力是并存的，也是发挥学生主动性，培养学生创造力的重要组成部分。因此，如何在数学教育中融入直觉思维，是每个教育者所关心和关注的。