利用数学思想方法解决方程类问题

文吴 叶

一、整体思想

整体思想方法在解方程（组）等方面有广泛的应用，整体代入、整体运算、整体设元、整体处理等都是整体思想方法在解数学问题中的具体体现。

例1 阅读下面的材料，解决问题：

解方程x4-5x2+4=0。这是一个一元四次方程，根据该方程的特点，它的解法通常是：

设x2=y，那么x4=y2，于是原方程可变为y2-5y+4=0，解得y1=1，y2=4。

当y=1时，x2=1，∴x=±1；

当y=4时，x2=4，∴x=±2；

∴原方程有四个根：x1=1，x2=-1，x3=2，x4=-2。

请参照例题，解方程（x2+x）2-4·（x2+x）-12=0。

【分析】根据阅读材料中的例子和换元法可以解答本题。

解：设x2+x=y，原方程可变为y2-4y-12=0，解得y1=6，y2=-2。当y=6 时，x2+x=6，得x1=-3，x2=2；当y=-2 时，x2+x=-2，得方程x2+x+2=0，∵Δ=b2-4ac=12-4×2=-7＜0，此时方程无实根。所以原方程有两个根：x1=-3，x2=2。

【点评】本题考查用换元法解一元二次方程，解答本题的关键是读懂材料，明确题意。

二、转化思想

解一元一次方程，根据等式的基本性质，把方程转化为x=a的形式；解二元一次方程组，是把它转化为一元一次方程来解；类似地，解三元一次方程组，是把它转化为二元一次方程组来解；解一元二次方程，是把它转化为两个一元一次方程来解。各类方程的解法不尽相同，但是它们有一个共同的基本数学思想，那就是转化，把未知转化为已知。

例2 一元三次方程x3+x2-2x=0，可以通过因式分解把它转化为x（x2+x-2）=0，解方程x=0 和x2+x-2=0，可得方程x3+x2-2x=0的解。

（1）问题：方程x3+x2-2x=0的解是x1=0，x2=，x3=；

【分析】（1）把左边的多项式进行因式分解，就达到了转化的目的，然后求解；

（2）对方程两边进行平方，就能把无理方程转化为整式方程，但要注意，由于出现了二次根号，所以要进行验根。

解：（1）x3+x2-2x=0，x（x2+x-2）=0，

x（x+2）（x-1）=0，所以x=0 或x+2=0 或x-1=0，∴x1=0，x2=-2，x3=1。

即x2-2x-3=0，（x-3）（x+1）=0，∴x-3=0或x+1=0，∴x1=3，x2=-1。

当x=-1 时所以-1 不是原方程的解。所以方程的解是x=3。

【点评】本题表面上看是考查一元二次方程的解法，实际上主要考查转化的思想方法。特别注意，我们在遇到解无理方程时需要验根。

三、分类思想

分类讨论思想是中学阶段必须掌握的重要思想方法，在中考中经常会出现带有这种思想的考题。

例3 已知用2辆A型车和1辆B型车载满货物一次可运货10 吨；用1辆A型车和2 辆B型车载满货物一次可运货11 吨。某物流公司现有31 吨货物，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满货物。

根据以上信息，解答下列问题：

（1）1 辆A型车和1 辆B型车都载满货物一次可分别运货多少吨？

（2）请你帮该物流公司设计租车方案；

（3）若A型车每辆需租金100 元/次，B型车每辆需租金120 元/次。请选出最省钱的租车方案，并求出最少租车费。

【分析】（1）根据“用2 辆A型车和1 辆B型车载满货物一次可运货10吨”和“用1 辆A型车和2 辆B型车载满货物一次可运货11吨”可以分别列出方程，组成方程组后进行求解；

（2）由题意理解出：3a+4b=31，解此二元一次方程，求出其整数解，得到三种租车方案；

（3）根据（2）中所求方案，利用A型车每辆需租金100 元/次，B型车每辆需租金120 元/次，分别求出租车费用即可。

解：（1）设每辆A型车、B型车都装满货物一次可以分别运货x吨、y吨，依题意列方程组得：

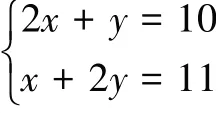
答：1 辆A型车装满货物一次可运3 吨，1 辆B型车装满货物一次可运4吨。

（2）结合题意和（1）得：3a+4b=∵a、b都是正整数或

答：有3 种租车方案。A型车9辆，B型车1 辆；A型车5 辆，B型车4辆；A型车1辆，B型车7辆。

（3）∵A型车每辆需租金100 元/次，B型车每辆需租金120 元/次，

∴方案一需租金：9×100+1×120=1020（元）；方案二需租金：5×100+4×120=980（元）；方案三需租金：1×100+7×120=940（元）。

∴最省钱的租车方案是方案三：A型车1 辆，B型车7 辆，最少租车费为940元。

【点评】本题主要考查了分类的思想方法，对可能出现的结果需要加以分类讨论，并归纳总结得出答案。

如果我们对数学进行简单的理解，那么数学就可以看成由显性的数学知识技能和隐性的数学思想方法两部分组成。对于方程这一板块来说也是如此。所以，学好方程这一板块的知识体系是基础和前提，利用方程这一板块的数学思想方法来解决问题是关键和目标。