《最短路径问题》一课的教学与思考

孙伟 蒋广权

《最短路径问题》这节课的主要内容是利用轴对称研究某些最短路径问题。怎样才能激发学生的学习兴趣，激活思维呢？

一、 创设情境，感知数学思想

活动1 展示问题1： 如图1，我快递公司每天要派快递员从北雅出发前往开福一中送货，途经一条笔直的芙蓉北路。想在芙蓉北路上建一个中转站，建在什么地方，可使路径最短？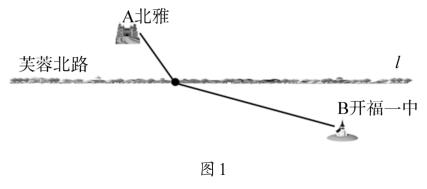

师生活动： 学生尝试将A，B两地抽象为两个点，将芙蓉北路抽象为一条直线，并相互补充，最后师生达成共识——已知： 一条直线l和直线异侧两点A、B。求作： 直线l上一点C，使得AC+CB最小。

点评： 情境设计为学生创设了轻松愉悦的课堂氛围，激活了学生思维；将实际问题抽象为数学问题，为学生探究新知搭建了台阶。

二、 探究新知，体会数学思想

活动2 出示课件： 如图2，快递公司想在芙蓉北路上建一个中转站，快递员每天从中转站出发前往北雅、长雅两地，请问中转站建在什么地方，可使路径最短？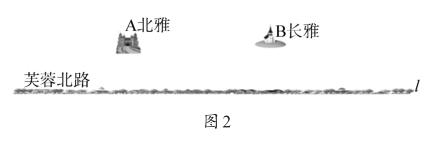

师生活动： 达成共识——已知： 一条直线l和直线同侧两点A、B。求作： 直线l上一点C，使得AC+CB最小。

师生讨论： 是否存在这样的点C？有多少个这样的点？教师引导学生使用几何画板验证。追问： 如果不用几何画板，有没有办法找到这个点？如果有，怎么找？教师引导学生通过轴对称的知识将同侧问题转化为异侧问题来解决，学生动手操作。再次追问： 我们可以用什么知识来解释它的正确性？

点评： 教师的二次追问，将新的问题转化为原来熟知的问题，巧妙地将转化数学思想内化在学生心中。

三、 巩固练习，强化数学思想

活动3 出示课件： 如图6（图略），在等边△ABC中，点E是线段AB的中点，AF是BC边上的高，在AF上求作一点P使得△BEP周长最小。

学生完成后，进行交流，师生点评。

点评： 学生又一次在探索问题中强化对转化数学思想的认识。

四、 探究拓展，深化数学思想

活动4 设置情境： 中欧班列线路规划将经过两个村庄A，B，两村庄之间有一条河，要在河上建设一座桥，使得列车在两村庄之间所走的路径AMNB最短，请问桥应该建在哪个位置？（假定河的两岸是平行的直线，桥要与河垂直。图略。）出示问题1： 从题目中能找到哪些已知条件？问题2： 如果不考虑路径最短，桥的选址有多少种情况？问题3： 能否直接看出桥MN的位置选在哪里，AM+MN+NB最小？问题4： 这个图与我们前面所讲的哪个图形类似，有什么共同点？ 能否转化成前面的问题？

师生活动： 学生独立思考，画图分析，组内交流作法，全班展示成果。

点评： 学生经过二次转化，首先要将生活问题转化为数学问题，其次，通过平移将复杂的最短路径问题转化为最原始的异侧最短路径问题。

五、 课堂小结，回归生活

活动5 课堂小结： 这节课我们解决了几个问题？主要用到了什么数学知识，体现了什么数学思想，你还有什么疑惑？

六、 教学反思

好的課题学习课，要有贴近学生生活的情境设置，应该指向社会生活，才能有效调动学生的积极性，更好地达成教学目标。数学学科的课题学习的目的在于使学生经历观察、猜想、验证、探究、推理、归纳等过程，培养学生发现问题解决问题的能力，提高数学核心素养。教学设计中，我们给予学生充分的时间进行探究，直至学生发现可以利用轴对称的方法将问题划归为已经解决过的问题。从实际上课的效果可以发现，不少学生逐步具备了化归的数学思想，比较顺利地解决了这个问题。

（作者单位：湖南省长沙市开福区周南秀峰学校）