联系熵方法在水资源承载力评价中的应用
金菊良 刘鑫 周戎星 崔毅 张浩宇 陈鹏飞


摘要:为准确描述联系熵的概念内涵和数学表达形式,反映联系熵的意义,采用联系数与信息熵、联系熵相结合分析的方法,提出了反映集对事件的内部不确定性状态和有序性发展的改进的联系熵,并通过安徽省水资源承载力评价实例与现有的联系熵计算方法进行对比分析,结果表明:改进的联系熵方法计算的各年份安徽省水资源承载力的等级评价结果与平均联系数评价、减法集对势、效应全偏联系数比较分析结果一致,相关系数非常接近1.0;改进的联系熵计算简便、适用性强、结果合理,可为集对事件的有序性发展提供新的判断方法。
关键词:水资源承载力评价;联系数;联系熵;有序性;安徽省
中图分类号:TV213
DOI:10.16152/j.cnki.xdxbzr.2020-03-015
The application of link entropy method in water resources
carrying capacity evaluation
JIN Juliang1,2, LIU Xin1,2, ZHOU Rongxing1,2, CUI Yi1,2,ZHANG Haoyu1,2, CHEN Pengfei1,2
Abstract: In order to describe the concept connotation and mathematical expression of link entropy more accurately, and reflect the meaning of link entropy, this paper uses the method of combination analysis of connection number, information entropy and link entropy, proposes the improved link entropy, which reflects the internal uncertain state and ordered development of the events of set pair, and through the comparative analysis of the water resources carrying capacity evaluation instance in Anhui Province and the existing link entropy calculation method, the results show that the improved method of link entropy to calculate each year level in Anhui Province of the water resources carrying capacity evaluation of the evaluation results, the average connection number, subtraction based set pair situation, and the effect full partial connection number all comparative analysis results are consistent, and their correlation coefficient is very close to 1.0. The improved method is simple, applicable and reasonable, and can provide a new method for judging the order of set pair events.
Key words: water resources carrying capacity evaluation; connection number; link entropy; order; Anhui Province
联系熵是由中国学者赵克勤[1]在集对分析的基础上提出的,它通过计算联系数的联系分量进一步导出,是联系数重要的伴随函数[2-6]。联系熵适用于度量事件发展的有序与无序、反映集对事件的内部混乱状态,可用于脆性复杂系统研究、风险及安全评价、教学测量与评价等领域。韦琦等[7]根据物理熵、信息熵、集对分析等理论提出脆性联系熵,建立了在复杂系统中的脆性仿真模型,当复杂系统达到临界熵值说明其崩溃,为复杂脆性系统研究分析提供了新思路。王莉等[8]将联系熵方法应用于煤矿安全-事故这一集对事件的预评价中,对指标等级标准值进行熵值计算划分等级,再对样本指标值进行熵值计算,为煤矿安全预评价等不确定性系统分析问题提供了新方法,为更多的安全预评价问题提供了计算简单且结果较为精确、可靠评价方法。郑岁华等[9]将联系熵应用于教学質量与评价中,依据熵与序的关系说明了学生的学习与教学过程的有序性密不可分,表明了联系熵方法用于教学测量与评价中有一定的可行性和适用性。目前,应用比较广泛的联系熵计算方法[8]在刻画联系熵的物理内涵方面尚未能明确反映同异反3个方面,为此,本文从联系熵的内涵出发,提出先计算联系数再计算隶属度最后应用到联系熵公式中,得到改进的联系熵计算公式,进而应用于安徽省水资源承载力评价中,并将该计算结果与已有的安徽省水资源评价方法进行对比分析。
1 联系熵的计算
1.1 信息熵
1864年德国物理学家克劳修斯(C1ausius)第一次提出熵的概念,即物体从外界吸收了热量,物体有ΔS的熵增。后来玻尔兹曼给出统计物理学热力学熵的表达式[7]:
式中,aij,bij,cij分别为样本i评价指标j联系数的同一度、差异度、对立度值,aij+bij+cij=1。wj为指标j的权重,uij是样本i评价指标j对应的联系数值。
聯系熵可通过同异反熵反应集对事件联系的程度,这里根据式(10)来确定各指标联系熵和等级联系熵。首先确定各等级临界值的标准联系熵以及评价指标值联系熵,若待评价指标值联系熵落入某标准联系熵区间,则判断待评价指标值即为该区域的评价等级。
3 实例分析
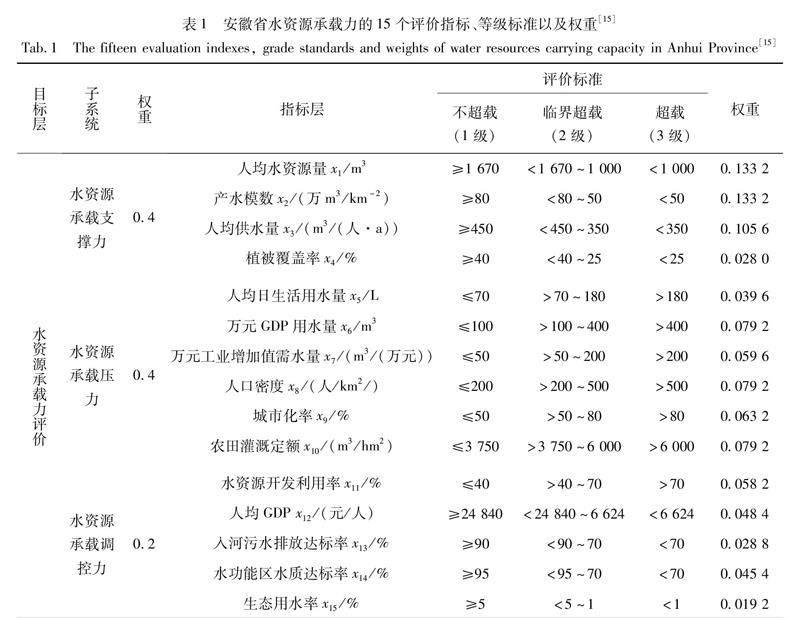
应用上节的步骤1~5对安徽省2005—2015年水资源承载力进行评价。参考文献[15]中给出的安徽省水资源承载力15个评价指标、等级标准以及权重见表1。
根据《安徽省水资源公报》《安徽省统计年鉴》收集的数据整理得到2005—2015年安徽省水资源承载力各评价指标的相关数据资料[27],采用上节所述的评价步骤1~3计算各年评价指标值联系数,为节省篇幅,现选部分年份的计算结果列于表2中。
由表2可通过步骤4~5进一步计算得到联系熵结果,见表3。
通过表1中等级标准数据可知表3中等级阈值s1和s2分别表示1.5级和2.5级。再对各年份联系熵进行线性内插划分具体等级,可得各年份联系熵及等级标准联系熵(见表4)。再将本文计算得到的2005—2015年安徽省水资源承载力评价结果与平均联系数评价[15]、减法集对势评价[3]、效应全偏联系数评价[4]的结果进行比较分析,如表4和图1所示。
由表4和图1可知:①联系熵值总体在减小,表明了安徽省2005—2015年水资源承载力状况在缓慢的波动中呈逐渐改善的趋势,这与图1中其他3种评价结果一致。②2005—2007年联系熵值较高,水资源承载力比较弱,2010,2014和2015年联系熵值较低,水资源承载力比较强,其余年水资源承载力一般。这说明水资源承载力具有波动性,这主要与指标“人均水资源量”“产水模数”具有波动性有关。联系熵评价结果与平均联系数评价结果的变化趋势相一致,并且两种方法的计算结果也比较接近,联系熵与减法集对势、效应全偏联系数的评价结果有明显的对称趋势,且在这3种方法下,安徽省水资源承载力强弱变化呈现出步调、幅度一致,表明联系熵评价与这些方法的评价结果相一致。
选取文献[4]和[15]中安徽省水资源承载力指标中4种具有代表性的评价指标,即人均水资源量x1、万元GDP用水量x6、万元工业增加值需水量x7和人均GDPx12,计算以上4种评价指标的联系熵评价等级、平均联系数评价等级、减法集对势、效应全偏联系数值进行比较分析,结果如图2所示。
由图2可知:①人均水资源量x1在2006年、2011年、2013年时往熵增的方向波动,在2010年、2015年往熵减的方向波动,同时与图1中这5年的变化是比较一致的,说明人均水资源量x1是这几年里导致全省水资源承载力变化状况明显的主要因素之一;可以看出联系熵评价在波动点处比平均联系数评价值表现明显,但总体与平均联系数评价、减法集对势、效应全偏联系数的结果变化趋势一致。②万元GDP用水量x6在2005—2015年联系熵评价等级在2.5以下且是熵值逐渐递减的过程,没有明显熵增与熵减之间的波动,且从2011年开始往后评价等级处在1.5到1.7之间且是随着时间逐渐往熵减的趋势(可载)方向发展,所以万元GDP用水量x6是改善全省水资源承载力的主要因素。③万元工业增加值需水量x7在2005—2009年的联系熵评价虽状况逐渐转好但等级均大于2.5,这对于图1中这5年联系熵评价等级均大于2.0是一致的。同时在2010—2015年万元工业增加值需水量x7联系熵评价等级逐渐熵减,并且整体在1.7级左右,这对于图1中这6年联系熵评价等级基本上小于于2.0是有影响的。说明万元工业增加值需水量x7也是改善全省水资源承载力的主要因素。④人均GDPx12在2005—2010年联系熵评价等级呈现逐渐熵减,在2009年前熵值均大于2.0,2009年后熵值均小于2.0,情况与万元工业增加值需水量x7的2011—2015年熵值变化比较相似,说明人均GDP x1也是改善全省水资源承载力的主要因素。⑤联系熵方法与平均联系数方法得出4种指标的计算结果比较一致,这两种方法的相关系数为0.96,0.96,0.98和0.99,很接近1,这说明了联系熵和平均联系数评价最开始都是通过计算指标值联系数的相似点。联系熵方法与减法集对势、效应全偏联系数得出的结果一致,这表明本文提出的联系熵的改进是符合实际的。
4 结 论
提出了联系熵计算的改进公式,将联系数与联系熵结合得更密切,更深刻地表达了联系熵的内涵,计算结果可反映事件的发展趋势。通过改进的联系熵在安徽省水资源承载力评价中的应用,验证了联系熵评价方法的合理性,在安徽省水资源承载力评价的应用结果表明:①改进的联系熵相比之前的联系熵计算含义表达得更清晰、合理,适用性更广。②在安徽省水资源承载力评价中的应用结果表明,联系熵与平均联系数评价等级的结果相一致,且在实例中联系熵比平均联系数评价呈现出安徽省水资源承载力更加明显变好的状况。③经过实例应用表明在2005—2015年改进的联系熵对其内涵的表征是准确的,计算结果符合实际情况,具有较强的可行性及适用性,为水资源承载力评价提供一定的方法参考,为集对事件的发展有序性判断提供了新途径。
参考文献:
[1]赵克勤.集对分析与熵的研究[J].浙江大学学报(社会科学版),1992,6(2):68-75.
ZHAO K Q. Study on set pair analysis and entropy[J].Journal of Zhejiang University (Social Science Edition),1992,6(2): 68-75.
[2]赵克勤.集对分析及其初步应用[M].杭州:浙江科学技术出版社,2000.
[3]金菊良,沈时兴,郦建强,等.基于联系数的区域水资源承载力评价与诊断分析方法[J].华北水利水电大学学报(自然科学版),2018,39(1):1-9.
JIN J L, SHEN S X, LI J Q, et al. Assessment and diagnosis analysis method for regional water resources carrying capacity based on connection number[J].Journal of North China University of Water Resources and Electric Power (Natural Science Edition),2018,39 (1):1-9.
[4]金菊良,張浩宇,宁少尉,等.效应全偏联系数及其在区域水资源承载力评价中的应用[J].华北水利水电大学学报(自然科学版),2019,40(1):1-8.
JIN J L, ZHANG H Y, NING S W, et al. Effect full partial connection number and its application in evaluation of regional water resources carrying capacity [J].Journal of North China University of Water Resources and Electric Power (Natural Science Edition),2019,40(1): 1-8.
[5]CHEN Y Q.Application of Set Pair Analysis in Water Resources carrying capacity Assessment [J]. Advanced Materials Research,2014,10(36):1065-1069.
[6]CUI Y, FENG P, JIN J L,et al.Water resources carrying capacity evaluation and diagnosis based on set pair analysis and improved the entropy weight method[J].Entropy,2018,20(5),359.
[7]韦琦,金鸿章,郭健.基于脆性联系熵的复杂系统崩溃致因研究[J].自动化技术与应用,2003,22(4):1-4.
WEI Q, JIN H Z, GUO J. Study on the collapse of complex system by using brittle link entropy[J].Automation Technology and Application, 2003,22 (4):1-4.
[8]王莉,田水承,王晓宁.联系熵在煤矿安全预评价中的应用[J].中国安全科学学报,2006,16(9):129-133.
WANG L, TIAN S C, WANG X N. Application of connection entropy in safety pre-evaluation of coalmine[J].Chinese Journal of safety science, 2006,16 (9):129-133.
[9]郑岁华,蒋云良.联系熵在教学测量与评价中的应用[J].湖州师范学院学报,2004,26(1):111-115.
ZHENG S H, JIANG Y L. Application of connection entropy in the teaching test and evaluation[J].Journal of Huzhou Normal University, 2004,26 (1): 111-115.
[10]金菊良,张浩宇,陈梦璐,等.基于灰色关联度和联系数耦合的水资源承载力评价和诊断研究[J].灾害学,2019,34(1):1-7.
JIN J L, ZHANG H Y, CHEN M L, et al. Evaluation and diagnosis of agricultural drought vulnerability based on grey correlation and connection number coupling[J].Journal of Catastrophology, 2019,34 (1): 1-7.
[11]SONG X M,KONG F Z,ZHAN C S.Assessment of water resources carrying capacity Tianjin in City of China[J]. Water Resources Management,2011,25(3).857-873.
[12]王友贞,施国庆,王德胜.区域水资源承载力评价指标体系的研究[J].自然资源学报,2005,20(4):597-604.
WANG Y Z, SHI G Q, WANG D S. Study on evaluation index of regional water resources carrying capacity[J].Journal of Natural Resources,2005,20(4):597-604.
[13]金菊良,沈时兴,陈梦璐,等.遗传层次分析法在区域水资源承载力评价指标体系筛选中的应用[J].华北水利水电大学学报(自然科学版),2019,40(2):1-6,15.
JIN J L, SHEN S X, CHEN M L, et al. Application of genetic analytic hierarchy process in screening in the evaluation index system of regional water resources carrying capacity[J].Journal of North China University of Water Resources and Electric Power (Natural Science Edition),2019,40 (2): 1-6,15.
[14]LIU Q Y, WANG M W,WANG X,et al.Land eco-security assessment based on the multi-dimensiona-l connection cloud model[J]. Sustainability,2018,10(6):2096.
[15]李辉,金菊良,吴成国,等.基于联系数的安徽省水资源承载力动态诊断评价研究[J].南水北调与水利科技,2018,16(1):42-49.
LI H, JIN J L, WU C G, et al. Dynamic evaluation and diagnostic analysis for water resources carrying capacity in Anhui Province based on connection number[J].South to North Water Diversion and Water Conservancy Technology,2018,16 (1):42-49.
[16]ZHOU R X,PAN Z W,JIN J L,et al.Forewarning model of regional water resources carrying cap-acity based on combination weights and entropy principles[J].Entropy,2017,19(11),574.
[17]金菊良,洪天求,王文圣.基于熵和FAHP的水资源可持续利用模糊综合评价模型[J].水力发电学报,2007,26(4):22-28.
JIN J L, HONG T Q, WANG W S. Entropy and FAHP based fuzzy comprehensive evaluation model of water resources sustaining utilization[J].Journal of Hydroelectric Engineering, 2007,26 (4): 22-28.
[18]景林艳.区域水资源承载能力的量化计算和综合评价研究[D].合肥:合肥工业大学,2007.
[19]范通达.水资源承载力评价及其在安徽省的应用研究[D].合肥:合肥工业大学,2007.
[20]陆君,舒荣军,李响,等.黄山市太平湖流域水资源承载力分析[J].复旦学报(自然科学版),2013,52(6):822-828.
LU J, SHU R J, LI X, et al. Analysis of water resources carrying capacity of Taiping Lake Basin, Huangshan City, Anhui Province[J].Journal of Fudan University (Natural Science),2013,52 (6): 822-828.
[21]刘童,杨晓华,宋帆.水资源承载力评价的Logistic集对分析模型及其应用[J].华北水利水电大学学报(自然科学版),2019,40(1):27-33.
LIU T, YANG X H, SONG F. Logistic set pair analysis model for water resources carrying assessment and its application[J].Journal of North China University of Water Resources and Electric Power (Natural Science Edition),2019,40 (1): 27-33.
[22]汪明武,金菊良.联系数理论与应用[M].北京:科学出版社,2017.
[23]金菊良,吴开亚,魏一鸣.基于联系数的流域水安全评价模型[J].水利学报,2008,39(4):401-409.
JIN J L, WU K Y, WEI Y M. Connection number based assessment model for watershed water security[J].Journal of Water Conservancy,2008,39 (4): 401-409.
[24]金菊良,董濤,郦建强,等.区域水资源承载力评价的风险矩阵方法[J].华北水利水电大学学报(自然科学版),2018,39(2):46-50.
JIN J L, DONG T, LI J Q, et al. Risk matrix method for evaluating regional water resources carrying capacity[J].Journal of North China University of Water Resources and Electric Power (Natural Science Edition),2018,39(2):46-50.
[25]陈守煜.水资源与防洪系统可变模糊集理论与方法[M].大连:大连理工大学出版社,2005.
[26]李辉,卞锦宇,周婷,等.基于联系数的区域水资源承载力诊断指标组合预测研究[J].华北水利水电大学学报(自然科学版),2018,39(3):18-23.
LI H, BIAN J Y, ZHOU T, et al. Combination forecast model based on connection number for diagnosis index of water resources carrying capacity[J].Journal of North China University of Water Resources and Electric Power (Natural Science Edition),2018,39(3):18-23.
[27]安徽省统计局, 国家统计局安徽调查总队.安徽统计年鉴(2001—2015版)[M].北京:中国统计出版社.
(编 辑 亢小玉)
收稿日期:2020-01-14
基金项目:国家重点研发计划资助项目(2018YFC0407206); 山东省重点研发计划资助项目(2017GSF20101); 国家自然科学基金资助项目(51709071)
作者简介:金菊良,男,江苏吴江人,博士,教授,从事水旱灾害研究。
通信作者:周戎星,女,安徽合肥人,讲师,从事水资源系统工程研究。

