基于直扩超宽带的超声波人体通信技术仿真

刘娇蛟 王倩倩 马碧云

(华南理工大学 电子与信息学院，广东 广州 510640)

无线终端的小型化、低功耗和低成本使人们对人体范围内的无线信息交换兴趣越来越大。因此，把体内、体表和人体周围的传感器、便携式终端等通过人体通信技术连接起来构成无线体域网(WBAN)[1]成为近年来的研究热点。其中，人体通信技术把人体作为信号的“传输线”[2]，是构建无线体域网的关键所在，在移动医疗和健康监护中有着重要的作用。利用该技术实现植入式人体通信可应用在个体化用药、基于植入体的原位监测、受控药物输送等方面；可以提供长时间连续、准确的生命体征监测；还可用于监测复杂身体部位的状况。例如，在神经末稍处的药物输送装置或神经刺激器可提供有效的治疗效果。

现有人体通信技术的研究面临不同的挑战[1]。其中射频通信技术[1，3]在人体通信应用中存在吸收率高、长期辐射危害大、RF波段拥挤等问题[4]；电容耦合人体通信[1，5]的发送端和接收端必须形成对地回路，不适合植入式人体通信；电流耦合型人体通信[1，5]由于受到通信频率的限制，其通信速度较低。相比之下，超声波自1960年应用于医疗以来，在已知的应用中未对人体产生副作用，并且在临床治疗和诊断中证明功率受限的超声波应用于人体是基本安全的[6]。此外，超声波无线能量传输系统应用于植入式医疗的研究也取得了进展[7]。

近年来，超声人体通信技术逐渐引起国内外学者的关注，但该技术面临的主要问题是：各种人体组织的密度不同，超声信号在传输中遇到不同组织产生的反射和散射会引起严重的多径效应。Santagati等[8]提出了超声波宽带(UsWB)技术，发射信号采用极短脉冲可以避免接收信号的直达波与多径信号混叠在一起，从而避免多径混叠造成接收端的误判；极短脉冲的低占空比可降低对人体有害的热效应和机械效应的影响。因此，理论上UsWB可安全有效地应用于体内通信。

为了实现体内多个节点之间的通信和组网，现有UsWB超声人体通信的方案中，每帧的时隙数量决定了体域网的节点接入数量，采用跳时(TH)模式难以维持节点数大于时隙个数的并发通信；简单地增加时隙数以达到增加接入节点数量的方法会导致通信速率降低。此外，UsWB中的发射节点采用在不同时隙中发射信号脉冲的方式，数据传输速率较低，而减少时隙个数会使得不同节点传输脉冲的冲突率增加，导致通信误码率(BER)增大。

鉴于UsWB在组网应用中存在的不足，本研究提出一种直扩超声波宽带(DS-UsWB)技术，采用直接序列扩频(DS)技术、信道编码和超宽带技术。相比之下，DS技术采用伪噪声(PN)序列来扩展信号，在相同误码率条件下可支持更多节点的并发通信；DS技术允许多个节点在同一时隙中传输脉冲，提高了通信的数据传输速率，如果结合信道编码可以进一步抵抗信道和多址干扰。

本研究通过人体信道的冲激响应模型分析超声人体通信的多径效应，从而确定发送信号脉冲的最小宽度，以克服多径效应造成的脉冲间干扰(IPI)。本研究还对DS-UsWB系统的信噪比、误码率和数据传输速率进行了理论推导。理论和仿真结果均表明，本研究提出的DS-UsWB技术比现有的UsWB技术具有更低的误码率和更高的数据传输速率。

1 人体信道分析

1.1 声波传输方程

声波在生物组织中传播时，声波的压力、密度、粒子速度等产生动态变化，这个变化遵循基于介质质量、动量、能量守恒的一系列耦合的一阶偏微分方程。当小幅度声波通过均匀无损的流体介质传输时，上述一阶方程可以表示为如下3个方程[9]。

动量守恒偏微分方程为

(1)

质量守恒偏微分方程为

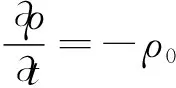
(2)

声波的压力和密度关系式为

(3)

其中，u为声粒子速度，p为声压，ρ为声密度，ρ0为周围介质密度，c0为等熵声速，t表示时间。由上述一阶方程组可以进一步导出声波的二阶波动方程：

(4)

超声波在吸收介质中传播时，设发送信号声压为p0，则传播距离为d的接收信号声压为[10]：

p(d)=p0e-αd

(5)

其中，幅度衰减系数α=α0fb[9]，单位为Np/cm，f是超声波信号的频率，α0(单位为Np/(m·MHzb))和b是超声波在组织中的衰减参数，b通常取值为1。

1.2 人体信道分析

超声波在人体组织中传播时，满足1.1中的三个一阶方程，传统的求解方法为数值法，如有限微分法。文献[11]采用k空间的伪谱法对声波的一阶方程组求解，Matlab的k-Wave[12]工具箱利用这一方法模拟声波在人体组织中的传播。伪谱法利用快速傅里叶变换降低了空间计算复杂度；k空间法在时域利用k空间传播算子方程组来近似时间导数，相比传统的数值法，减少了计算时间[12]。

在k-Wave中通过设置人体组织的形状和相应的参数(如声速、密度、衰减系数等)，建模人体的不同部位。利用圆柱体对三维人体手臂进行建模，手臂长度为20 cm，半径为5 cm，皮肤层厚度为3 mm，脂肪层厚度为7 mm，肌肉层厚度为22 mm，骨头半径为18 mm。图1为k-Wave仿真的手臂模型三视图截图，坐标轴表示手臂位置信息，k-Wave工具箱默认设置各个方向的中心位置为0 。图1中TX表示发送传感器的位置，RX表示接收传感器的位置。其中，人体组织的参数设置如表1所示。

在肌肉层相距15 cm位置处各放置一个发送传感器和接收传感器，发送信号采用狄克拉脉冲。图2为仿真过程中某一时刻超声波脉冲在手臂中的传播图，超声波不同声压值对应不同的灰度值，传播过程中声压的衰减规律符合式(5)。对接收传感器收到的时间序列进行归一化处理，可以得到手臂信道的归一化冲激响应，如图3所示，接收端收到的是多个脉冲的组合，且由于脉冲足够窄，脉冲间未产生混叠和干扰。

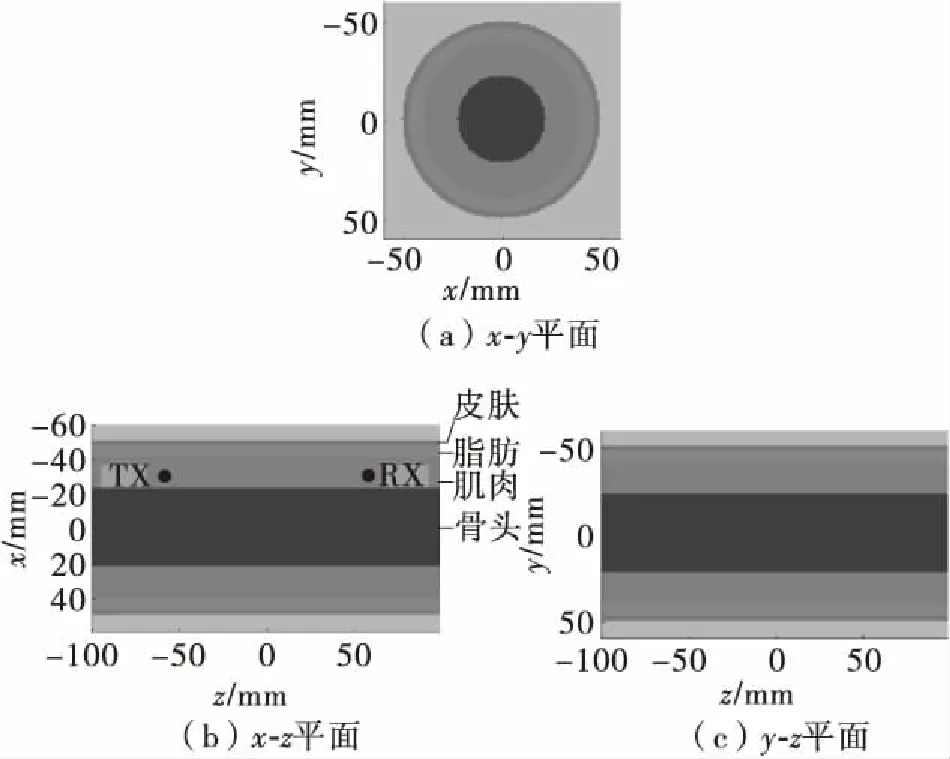
图1 三维手臂建模的声速分布图

Fig.1 Sound velocity distribution of 3D arm modeling

表1 组织参数[13]

图2 手臂中超声波脉冲传播

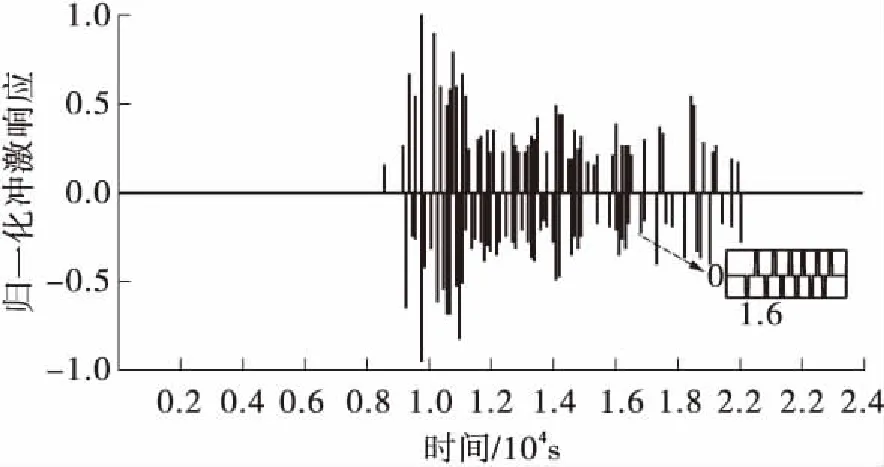
图3 三维手臂模型的归一化信道冲激响应

(6)

其中，δ表示狄拉克函数。人体通信的接收信号y(t)可以表示成信道冲激响应h(t)与发送信号x(t)的卷积，即y(t)=h(t)*x(t)。此外，人体信道冲激响应的建模方法同样适用于人体其他部位，可以得到对应的信道模型并进行特性分析。

分析图3可知，在手臂不同组织的分界面会产生反射和折射，导致接收端的归一化信道冲激响应不是单一脉冲，而是多个脉冲的组合，这就体现了人体信道的多径特性。如果发送的脉冲宽度足够短，通过人体信道的多路延时信号不会出现重叠，就可以在接收端分离出直达脉冲，有效避免了多径混叠造成的误判。因此，为了克服多径效应，需要对人体信道冲激响应的多径时延特性进行分析，确定发送脉冲的宽度。测量图3中相邻脉冲间的间隔，可以得到信道冲激响应的最小脉冲间隔为500 ns，因此当发送信号脉冲宽度小于500 ns，就可以避免多径脉冲信号重叠，有效克服脉冲间干扰(IPI)[14]。

2 系统结构原理

2.1 直扩超声波宽带系统架构

直扩超声波宽带(DS-UsWB)系统发射端架构如图4所示，待发送二进制序列g通过信道编码、扩频调制、二进制相移键控(BPSK)和脉冲成形后，经过超声波换能器发射超声波信号。

图4 直扩超声波宽带系统发射端

Fig.4 Transmitter end of direct-sequence ultrasonic wideband system

图4中脉冲形成器的输出s(t)可表示为

(7)

其中，Tc为发送脉冲的时隙宽度，脉冲宽度由体内多径脉冲信号的最小时延间隔决定，p(t)是高斯脉冲的二阶导数，是超宽带通信中最普遍采用的脉冲波形[14]：

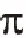
(8)

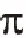
图5为DS-UsWB系统发送示例波形，发送g=1，正交扩展码SC={1，1，-1}，PN序列PN={1，-1，1，-1}。其中，帧长Nh=4，码长Ns=3，图中时隙宽度为Tc，帧时间长度为Ts，且Ts=NhTc。

图5 DS-UsWB系统发送示例

在接收端对第1条到达的路径信号进行判决。只要脉冲宽度小于第1条路径信号和第2条路径信号间的到达时间之差，多径分量就不会对第1条路径信号产生干扰。

2.2 理论性能分析

如果用Nh表示帧长，即每帧的时隙数。用Ns表示正交扩展码的码长，即正交扩展码的周期，为一个比特发送的帧数。采用DS-UsWB技术的系统通信数据传输速率(单位b/s)可以表示为[8]

(9)

可见，帧长和码长会对数据传输速率产生影响。如果不考虑功率控制策略[15]，接收端接收信号的信噪比(SNR)可以表示为

(10)

其中，Eb表示一个比特的信号能量，η表示一个时隙的体内平均噪声功率[8]。

在误码率分析时，首先考虑进行直接序列扩频(DS)发送超声波脉冲信号的系统，接收信号可表示为[16]

(11)

在接收端，DS系统SNRDS=Eb/(NhηTc)，系统采用BPSK调制和相关接收机，则DS系统的误码率Pe可表示为一个Q函数：

(12)

当K=0，没有干扰节点时，该误码率等同于BPSK的误码率。

信号进入DS系统前，采用正交扩展码进行信道编码，叠加信道编码的DS系统即为DS-UsWB系统，此时干扰节点只有与源节点使用相同的正交扩展码，才会对正在进行的通信产生干扰。当有K个干扰节点，正交扩展码长度为Ns时，DS-UsWB系统误码率表示为

(13)

上述分析表明，数据传输速率和误码率都受到帧长Nh和码长Ns的影响。因此，通过调整Nh和Ns可以同时改变数据传输速率和误码率。在通信中，数据传输速率越大，误码率越高，应根据误码率要求进行速率调整。

3 仿真分析

在k-Wave仿真中，发送节点和干扰节点的位置设置在距离接收节点15 cm处，且所有节点位于肌肉层，因此发送节点和干扰节点具有相同的信道特性。应用信道冲激响应h(t)，即式(6)，模拟人体信道进行多节点通信。所有节点使用相同的帧长Nh，系统发送端架构如图4所示，在接收端进行相关接收，仿真忽略同步误差，发送脉冲信号为高斯脉冲的二阶导数。

当系统中只有一对通信节点时，在帧长Nh不同的条件下，DS-UsWB系统误码率与信噪比的关系见图6。可以看出随着信噪比的增加，系统误码率下降，在Nh=4，Ns=1的条件下，信噪比为4 dB时就可以实现BER=10-4的误码率性能。在相同信噪比时，随着Nh的增加，系统误码率会进一步下降，可见调整Nh会对系统误码率产生显著影响。

图6 不同信噪比下的DS-UsWB系统仿真误码率

Fig.6 System simulation BER of DS-UsWB under different SNR

为了与现有UsWB系统的误码率性能进行比较，可以将误码率处理增益[17]表示为

(14)

其中，Pe(TH)是TH系统[8]的误码率，Pe(DS)是DS系统的误码率。误码率处理增益G>1 时，表明DS系统误码率小于相同条件下的TH系统误码率。在Matlab中仿真第2.2节中DS系统和DS-UsWB系统的理论误码率，并分别与现有UsWB技术的TH系统和UsWB系统进行对比，结果如图7和图8所示。

图7示出了TH系统和DS系统的误码率与帧长Nh的关系，可见系统误码率均随着Nh的增加而减小，误码率处理增益G随Nh增加而增加。当Nh=15，干扰节点个数K=3和K=6时，误码率处理增益分别为32和10，这表明在相同条件下，DS系统误码率优于TH系统。对于相同的误码率，DS系统的Nh更小，可达到更高的数据传输速率。

图7 不同帧长的系统误码率

图8 不同扩展码码长和不同帧长的误码率

Fig.8 BER of different frame length and different length of spreading code

当干扰节点个数K=3时，UsWB和DS-UsWB系统误码率与Nh和Ns的关系见图8。可见随着Ns增加，两个系统的误码率进一步降低，且在相同条件下，DS-UsWB的误码率比UsWB低。对于相同的误码率和Ns，DS-UsWB的帧长Nh明显小于UsWB，这表明DS-UsWB数据传输速率大于UsWB。例如，对于Ns=3，为了实现BER=10-3，DS-UsWB的Nh等于2，而UsWB的Nh等于15，因此，理论上DS-UsWB的数据传输速率此时是UsWB的7.5倍。

在Matlab中进行DS-UsWB多点通信仿真时，设置脉冲宽度为500 ns，设置扩展码长度Ns=10，干扰节点个数K=3，所有节点同时发送数据。图9对比了接收端测量的误码率和UsWB在相同条件下的误码率。仿真结果表明，相同帧长和码长条件下，DS-UsWB系统误码率优于UsWB。而为了实现BER=10-4，DS-UsWB的Nh等于4，UsWB的Nh等于8，因此相同误码率下，DS-UsWB速率更高。根据式(9)可以计算，此时DS-UsWB的数据传输速率为33 kb/s，可满足现有的多数体内通信速率要求，例如，植入在皮下的血糖监测仪和植入在腹部的胰岛素泵的数据传输速率为32 b/s，植入在胸腔的起搏器数据传输速率为0.5 kb/s[18]。

图9 不同帧长的系统仿真误码率

4 结语

本研究提出了一种用于人体通信的直扩超声波宽带(DS-UsWB)技术。采用k-Wave对人体信道建模，求出信道冲激响应，并分析体内通信的多径效应，得出DS-UsWB克服人体信道多径效应的脉冲宽度条件。分析多节点干扰和信道噪声干扰，得出系统误码率(BER)的理论表达式。理论和仿真结果表明，与现有超声波宽带(UsWB)技术相比，本研究提出的DS-UsWB技术可达到更低的误码率和更高的数据传输速率。今后的研究方向是通过搭建超声波人体通信的实验平台，利用物理仿真实验对DS-UsWB技术进行验证，并进一步研究数据链路层的媒体接入控制。