连续压机活动式机架变形与热力耦合特性研究∗
陈光伟 李艳娜 花 军 陈相宇 林送峰
(1.东北林业大学机电工程学院,哈尔滨 150040; 2.黑龙江大学生命科学学院,哈尔滨 150080)
1 连续压机高压段活动式机架结构分析
对于连续平压式热压机(以下简称连续压机),机架是其重要的构成部分之一。由于连续压机在长度方向需要拟合人造板生产的压力曲线,因而处于不同区段的机架其承载不同[1]。热压过程中不同区段板坯状态和内部蒸汽压力各不相同,对热压过程中温度和热量有着不同的要求[2]。热压压力及温度对人造板生产过程的影响相互制约、又相互依存,因此在生产过程的工艺调整时需要进行统一分析。但是在连续压机的高压段,该段内机架不仅所受的载荷最大,而且所处的环境温度也最高[3-4]。因此,综合考虑热力耦合效应对高压段机架所造成的影响,对连续压机的结构设计及生产中的合理使用都有实际意义。
本文分析热力耦合效应对连续压机高压段机架产生的影响,所针对的是一种可活动式机架,在CPS型压机机架基础上进行机架结构设计。如图1所示,设计的活动式机架主体结构由上、下横梁2、11与左、右两侧的立柱5构成,立柱与上下横梁间通过销柱12铰接。立柱上端安装主油缸1,主油缸下端与上横梁连接,上热压板4通过上隔热板3安装于上横梁的下边缘;下横梁的上边缘与支撑座9相连,支撑座中部安装5个差动油缸10,支撑座两侧与下隔热板8相连,差动油缸与下隔热板之上安装下热压板7。压机工作时,通过主油缸带动上横梁运动,调节上、下热压板之间的距离,通过差动油缸输出不同的支撑力使热压板弯曲变形,从而使板坯由中间向两侧排气;同时要求横梁具有较高的刚度,在对板坯6热压时变形量要小,以此保证上热压板的平直。

图1 活动式机架结构图Fig.1 Structure of movable frame
本文所设计的活动式机架采用多块框板组合而成,比一般的框式机架结构具有更好的横向刚度,同时解决了压机侧面空间的敞开问题,能提高生产精度及使用寿命,同时为维护、保养和修理工作带来方便。一般连续压机机架设计过程中,机架结构参数主要依靠经验确定[5],连续压机机架结构尺寸较大,结构参数选取合理与否决定制造成本的高低,合理选取结构参数可节省材料消耗,降低生产成本。
2 连续压机高压段活动式机架受力变形分析
2.1 活动式机架主要结构参数
根据人造板生产热压工艺可知,连续压机入口段因板坯压制产生的变形量大、反弹力大,因而所需压力最高,故也称之为高压段,采用连续压机生产纤维板或刨花板时,高压段的压力受原料树种、板坯含水率以及板材的压制密度与厚度等多种因素影响,通常情况下其最大面压不超过5 MPa[6];因此,在该活动式机架结构设计中取设计面压为5 MPa。
人造板生产中,板坯进入连续压机入口段(即高压段)后需要高温加热,以使热量快速向板坯内部传递,促使胶液流动与固化;但热压板的实际加热温度受板坯含水率、生产板材的厚度及胶种等影响[7]。从现实生产情况看,目前采用连续压机生产人造板时多采取高温加热板坯的方式,高压段用于加热热压板的导热油温度最高可达240 ℃左右,热压板、钢带的加热温度可达220~230 ℃[8];由此,在后续热效应分析中取热源温度为230 ℃。
该活动式机架设计加工幅宽为9英尺(2 750 mm)的人造板,因热压板边缘还需安装热油管道、管道支架等附件,需对热压板安装面尺寸进行扩大[9],因此取机架上、下横梁热压板安装面宽度C为3 200 mm。考虑机架横梁两侧的加工圆角尺寸及立柱的安装尺寸,取横梁与立柱铰接点水平距离L为4 100 mm。另外,连续压机不同区段机架间距各不相同,因连续压机高压段所承受的载荷较大,对该区段机架具有较大的承载能力和刚度等要求,因此机架间距不宜过大[10],取机架间距为1 050 mm。
2.2 活动式机架的变形量计算
2.2.1 机架受力状况
若不考虑机架中可移动部分的重力,根据前述活动式机架的设计面压、热压板幅宽及机架间距等参数,计算机架工作中所需承受的总压力F(均布载荷)为:F=5.0×106×3.2×1.05=1.68×107N。
因该机架的上下横梁各由两块框板组合而成(见图1中机架的侧视图),故上横梁单一框板所受的最大压力Fmax为8.4×106N;下横梁共布置5个差动油缸和2个固定支撑,可视为受7个集中载荷作用,载荷大小为Fmax的1/7,为1.2×106N。根据文献[11]对压力机框架受力分析方法,取上下横梁与左右立柱的四个铰接点为框架节点,下横梁两端与立柱上端为固定端,并结合机架的结构尺寸,将机架各部分结构简化为梁形式,以线型梁架结构绘制机架的受力与变形简图如图2所示。

图2 活动式机架的受力与变形简图(虚线表示横梁的变形)Fig.2 The stress and deformation of movable frame(dotted line represents the deformation of the beam)
由图2可见,因该活动式机架具有4个活动铰接点,其受力变形状况与由整块钢板加工而成的框片式机架有很大的不同;活动式机架仅上、下横梁因受载荷作用会发生弯曲变形,但左右立柱仅受拉力作用,不存在弯矩,因此不会发生向内侧弯曲。
2.2.2 机架的变形量计算
1)立柱结构尺寸的确定。如前所述,因活动式机架的立柱仅受拉力作用,故其应力σ可用材料力学中拉杆受力公式直接计算[12],为:

式中,FH为横梁所受拉力,因每段机架包含4个横梁,故FH=Fmax/2;A为材料截面面积,A=B×d(B为截面宽度,mm;d为截面厚度,设计时取80 mm);σa为材料的许用应力,MPa。
若机架材料选用Q235b钢板,其许用应力σa为235 MPa,代入式(1)计算宽度B为:

即立柱最小截面宽度不应低于223 mm。设计该活动式机架的立柱结构时,考虑到立柱顶端需安装主油缸等部件,取最小截面宽度B为380 mm,约为限定值的1.7倍,故可以满足机架的使用要求。
2)上横梁的变形量计算。由图2可见,机架上横梁两端为活动铰接,构成对称简支梁,梁中部受均布载荷Fmax/C作用,位置尺寸包括:L=4 100 mm、C=3 200 mm。根据材料力学知识,上横梁的最大挠度发生在中点处[13],最大位移量δC为:
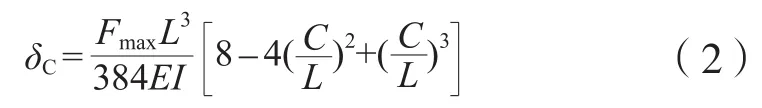
式中,E为弹性模量,Pa;I为上横梁截面的二次矩,m4。
将机架结构尺寸参数带入式(2),得上横梁最大变形:

3)下横梁的变形量计算。由机架受力状况分析,支撑座受下横梁支撑,与下横梁紧密接触,在横梁受力分析时将支撑座视为简支梁,受下横梁支点反力Fa作用,差动油缸压力转化为均布载荷Fmax/C作用,下横梁受力相应可视为在C范围内受均布载荷Fmax/C和在C距离上分别作用一个Fb/2的集中载荷,且下横梁最大挠度δD发生在中点处,下横梁受力变形简图如图3所示。

图3 下横梁受力与变形图Fig.3 The stress and deformation of beneath beam
下横梁受力后变形δD为[14]:

支撑座受力后变形δd为:

式中,Ib为支撑座截面的二次矩,支撑座高度取下横梁高度的1/8,Ib=I/512,m4
将式(3)、(4)带入变形协调条件δD/L=δd/C可知[15]:

将Fmax及下横梁位置尺寸带入式(5)中得Fb=3.246×106N,带入式(3)求解δD为:

4)活动式机架横梁总变形量计算及横梁高度尺寸确定。由计算所得的活动式机架上、下横梁变形量δC与δD,可知机架总变形δ为:

依据材料力学截面图形几何性质,矩形截面的二次矩I表达式为[16]:

式中:d为矩形截面的厚度,m;h为矩形截面的高度,m。
根据文献[14]关于液压机械横梁几何精度的相关内容,设计中上、下横梁的总弯曲变形允许值为0.24/1 000 mm,结合本文中机架横梁长度L=4 100 mm,上、下横梁最大总变形δ=0.984 mm。结合式(6)与(7),有:

横梁材料弹性模量E为2.05×1011Pa,横梁厚度d取80 mm,将以上数值代入式(8),计算得出上下横梁最小高度h应大于2 383 mm。对于连续压机这类压力机械而言,因其在工作中所受载荷为长期持续性加载,除横梁变形外,油缸、热压板等部件也会产生微小变形[17]。为此,将横梁最小高度尺寸h扩大圆整为2 500 mm;另据前述计算可知,上、下横梁在载荷作用下产生的变形量基本相等,因此设置上、下横梁最小高度均为1 250 mm。
3 连续压机高压段活动式机架热力耦合分析
3.1 活动式机架热力耦合模型建立
根据图4中活动式机架各零部件尺寸,利用SolidWorks软件进行三维建模,将模型导入Hypermesh软件,建立机架的热力耦合分析模型。采用映射网格划分技术对该模型进行高精度网格划分,热分析采用solid70三维实体热单元,结构分析采用solid185三维8节点固体结构单元,机架各部分结合面处用公共节点连接;对机架共划分出213 800个单元,298 337个节点。
定义机架材料属性:活动式机架主体由Q235b碳素结构钢板焊接而成,主油缸缸体及柱塞分别由HT300及45钢制成,隔热板与销柱使用的材料分别为YC200(非金属复合材料)与35钢。各材料具体性能参数如表1所示。

表1 活动式机架各部分材料属性Tab.1 Material properties of each part of movable frame
定义载荷及边界条件:活动式机架热量传递形式以传导换热为主,对流换热及辐射换热次之。机架所处环境温度设定为35 ℃,设置为环境热载边界条件;热压机工作时机架隔热板与热压板接触,热压板温度(热源)为230 ℃,因此隔热板表面温度也设定为230 ℃,并作为外热载边界条件;机架各部件结合面处通过公共节点定义热传导,根据文献[18]提出的物体对流和辐射组合表面换热系数计算方法,确定机架表面换热系数为h=10 W/m2.℃;下横梁底面设置为固定位移约束,根据活动式机架横向压力分布,设置上隔热板表面所受均布载荷为2 625 kN/m(即Fmax/C的值),下隔热板表面及支撑座共有7个集中载荷作用,取值为1 200 kN。
3.2 活动式机架热力耦合效应分析
3.2.1 机架温度场与热应力分析
采用ANSYS软件分析活动式机架在热载荷作用下的温度场分布及产生的热应力,求解得出其温度场分布与热应力分布,分别如图4a和图4b所示。

图4 活动式机架温度场分析结果Fig.4 Temperature field analysis of movable frame
根据温度场及热应力分布云图可以看出,因连续压机工作时隔热板与热压板长期接触,机架中温度较高的区域主要集中于上、下隔热板处。温度分布特点是:隔热板与热压板的接触面(图4a中黑色区域)温度最高为230 ℃,之后热量向上下横梁扩散,但扩散区域很小、温度降低很快,至热量扩散的边缘(图4a中浅灰色区域)温度已降至50 ℃左右,而上下横梁主体温度大部分保持在环境温度35 ℃左右(图4a中灰色区域)。机架中上横梁与下横梁支撑座温度梯度最大,因而产生的热应力也最大;热应力最大区域为上横梁中部及下横梁与支撑座结合处(图4b中黑色区域),最大值约为34.2 MPa。
3.2.2 机架热力耦合综合效应分析
利用ANSYS软件,分析热力耦合综合效应下活动式机架的应力与应变分布情况,结果见图5;其中,图5a为热力耦合效应下应力分布图,图5b为应变分布图。

图5 活动式机架热力耦合分析结果Fig.5 Thermal mechanical coupling analysis of movable frame
由图5可见,机架在热力耦合效应下最大等效应力约为173 MPa(图5a中黑色区域),最大应变约为1.585%(图5b中黑色区域),两者均出现在上横梁顶端中部。该现象产生的原因:一是机架为对称式结构,所受载荷也对称分布,因此应力、应变集中点必然出现在机架中间部位。二是机架上横梁为静定结构,下横梁为超静定结构,存在附加力偶,具有减小结构变形的作用,因此在载荷作用下上横梁变形以及应力与应变必然大于下横梁。三是若以主油缸与上横梁连接处作为固定点,由上横梁所受的均布载荷形成的力矩会使其发生凸起变形,因而在上横梁顶端产生的应力、应变必然最大。此外,由图4b所示的热应力分布图可见,上横梁中存在大面积的高应力区,会使得上横梁发生水平延展[19],这又会进一步加大其顶端的变形与应力、应变。
对比分析静载作用下活动式机架的应力与应变情况。为此,依然采用ANSYS软件分析活动式机架仅在静载条件(即不考虑热效应)下的应力与应变分布,结果如图6所示。
图6a所示为仅在静载作用下活动式机架的应力分布,其最大等效应力为151 MPa;图6b所示为机架的应变分布,最大应变为1.265%;但最大等效应力与应变的位置与图5相比出现了变化,是发生在主油缸与上横梁相连接的固定点内侧。产生这一现象的原因是,当仅考虑静力作用时,该处所受的弯矩最大,因而产生的应力与应变必然较大。图6中,虽然在上横梁上部中间位置也存在较大的应力(133 MPa)与应变(1.126%),但与热力耦合综合效应分析结果对比,还是存在较大的差异。

图6 活动式机架静力学分析结果Fig.6 Static load analysis of movable frame
以上分析结果表明:对于该活动式机架而言,热力耦合效应对机架结构的变形及其应力、应变状况的影响比较显著。其一方面造成了机架最大应力、应变位置的变化,另一方面,就两者的最大应力、应变值相比较,增幅分别为14.57%和25.30%。此外,就热力耦合综合效应下机架上横梁的最大应力值(173 MPa)来说,其已经非常接近Q235b材料使用时所要求的极限180 MPa[20],这说明在机架结构设计中,若忽略热效应的影响,可能会使机架强度不够,影响生产精度,甚至发生疲劳破坏。
4 结论
介绍了应用于连续平压式热压机的活动式机架各部组成及其结构,通过对机架主要构件的受载变形求解,确定了机架立柱与上、下横梁合理的结构尺寸,在满足使用要求基础上,可节省制造材料,节约生产成本。
以连续压机高压段的热压工艺参数为基础,建立了活动式机架的热力耦合效应分析模型,对活动式机架温度场进行分析,得出机架的热应力分布状况。通过求解热力耦合效应与静载作用下活动式机架的应力与应变分布,对比分析机架的最大应力、应变的数值与位置变化情况。结果表明:热力耦合效应会对机架的综合性能产生较大影响,在机架结构设计中不应忽略。
热力耦合分析表明:活动式机架上存在明显的温度梯度,热量由隔热板与热压板的接触面向上下横梁扩散,该试验条件下,热力耦合效应产生的最大等效应力约为173 MPa,最大应变约为1.585%,最大热力耦合应力应变均出现在上横梁顶端中部,为活动式机架结构性能的薄弱环节,在后续研究应重点关注。

