农村水电站压力管道水头损失计算

左保静， 王文全， 曹善宇

(江苏省水利工程科技咨询股份有限公司， 江苏 南京 210029)

农村水电站的压力管道是一种将水流从小水电站的进水口引到水轮机的引水管道。在压力管道中，水流一般为有压流，压强较大，速度较快，其水头损失一般可由沿程水头损失与局部水头损失组成，一般局部水头损失与沿程水头损失各自单独发生、互不影响，其总水头损失由两种水头损失叠加得到[1-2]〗。其中沿程水头损失一般按照水力手册中的公式进行计算，但相关计算公式较多，如何选取其中合适的公式是一个极为重要的问题；而局部水头损失一般发生在水流断面突然变化，如扩大、缩小等流线急剧弯曲、转折或流场中有明显局部障碍处，该类水头损失计算通常假定这些边界突变断面处为该类水头损失产生的位置，确定这些突变断面处的局部水头损失系数也是压力管道水头损失计算的重要问题之一。

本文首先归纳总结农村水电站压力管道水力计算所采用的基本计算理论与方法，之后选取适用于压力管道的水力计算公式对1.2 m3/s、1.6 m3/s、2.0 m3/s、2.4 m3/s、2.8 m3/s、3.2 m3/s流量下某农村水电站工程的压力管道进行计算，分析其水头损失随流量变化的规律，旨在为农村水电站新建或修复工程的增效提供参考。

1 农村水电站压力管道水力计算理论与方法

1.1 恒定总流伯努力方程

恒定总流伯努力方程可由式(1)表示。

(1)

伯努力方程作为水力学基本原理，其实质是流体机械能守恒。从该方程可看出，在液体流动过程中，其位能、压能、动能之间可以相互转化。值得注意的是，由于伯努力方程是由机械能守恒推导出的，该方程仅适用于黏度可以忽略、不可被压缩的理想流体。

1.2 沿程水头损失计算公式

沿程水头损失计算一般采用经典达西公式，其具体表达式可表示为

(2)

式中：λ为沿程水头损失系数；l为所求的沿程的距离，m；v为断面平均流速大小，m/s；R为水力半径，m；g为当地重力加速度，m/s2。达西公式给出了适用于均匀流的沿程水头损失与流速、流段长度、边界几何特征与阻力特征间的相互关系。在式(2)中的水力半径R是指过水面积和湿周比值，具体表达式为

(3)

式中：A为过水面积，m2；χ为湿周，m。过水断面湿周χ反映水流横向边界阻力特征，湿周越大水流阻力及相应的水头损失就越大。

过水面积A主要反映水流横向边界几何特征对过流能力的影响，过水面积A越大过流能力越强，但对反映边界阻力状况却不能很好地反映。面积相同而形状不同的过水断面具有不同的湿周，边界产生的阻力和形成的水头损失也不相同。对于圆断面与矩形断面，水力半径公式可具体表示为

(4)

式中：D为圆断面直径，m；b为矩形断面宽度，m；h为矩形断面高度，m。

除水力半径之外，沿程水头损失计算还需确定沿程水头的损失系数λ，一般与水流的流动形态、边界条件相关。

在收集了丰富的水力试验资料基础以及长期的实践工作，学者们以谢才公式反映沿程水头损失系数：

(5)

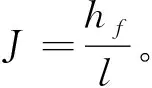
(6)

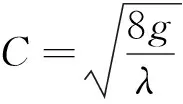
谢才公式既适用于引水渠道水流也能用于管流计算，它的谢才系数计算一般采用巴甫洛夫斯基公式或曼宁公式。

巴甫洛夫斯基公式表达式如下：

(7)

式中：nb为巴甫洛夫斯基公式粗糙系数；指数Y按下式计算：

(8)

近似计算时，可取

(9)

曼宁公式的表达式如下：

(10)

式中：R为水力半径，m；n为粗糙系数，可由实测或查表确定。

由式(7)与式(10)可看出：当y=1/6时，巴甫洛夫斯基公式可退化为曼宁公式。

对于农村水电站的压力管道而言，它的沿程水头损失系数一般选用海曾-威廉公式计算。海曾-威廉公式的表达式如下：

(11)

式中：q为流量，m3/s；Cw为海曾-威廉粗糙系数，可通过查表得到。

将式(11)代入达西公式(1)，可得到：

(12)

1.3 局部水头损失计算公式

局部水头损失产生于水流边界的明显改变位置，是水流流态发生较大变化引起的，这种能量损失只出现在边界改变前后的局部流段范围内，具有能耗大、能耗集中和主要是涡漩损失这三个特点。

理论和实验研究都表明，局部水头损失主要和边界改变形式以及水流速度相关，可写成如下形式：

(13)

式中：v为断面平均流速，m/s；ξ为局部水头损失系数。

2 工程实例计算

图1为某农村水电站的混凝土压力管道示意图。从图可看出：该结构总长27m，其中渐变段长1m，管道直径1.2m，进水口中心线与压力管道出口中心线高差19m，进水口与压力管道出口之间的水平长度16.25m，管道与水平面夹角40°左右。

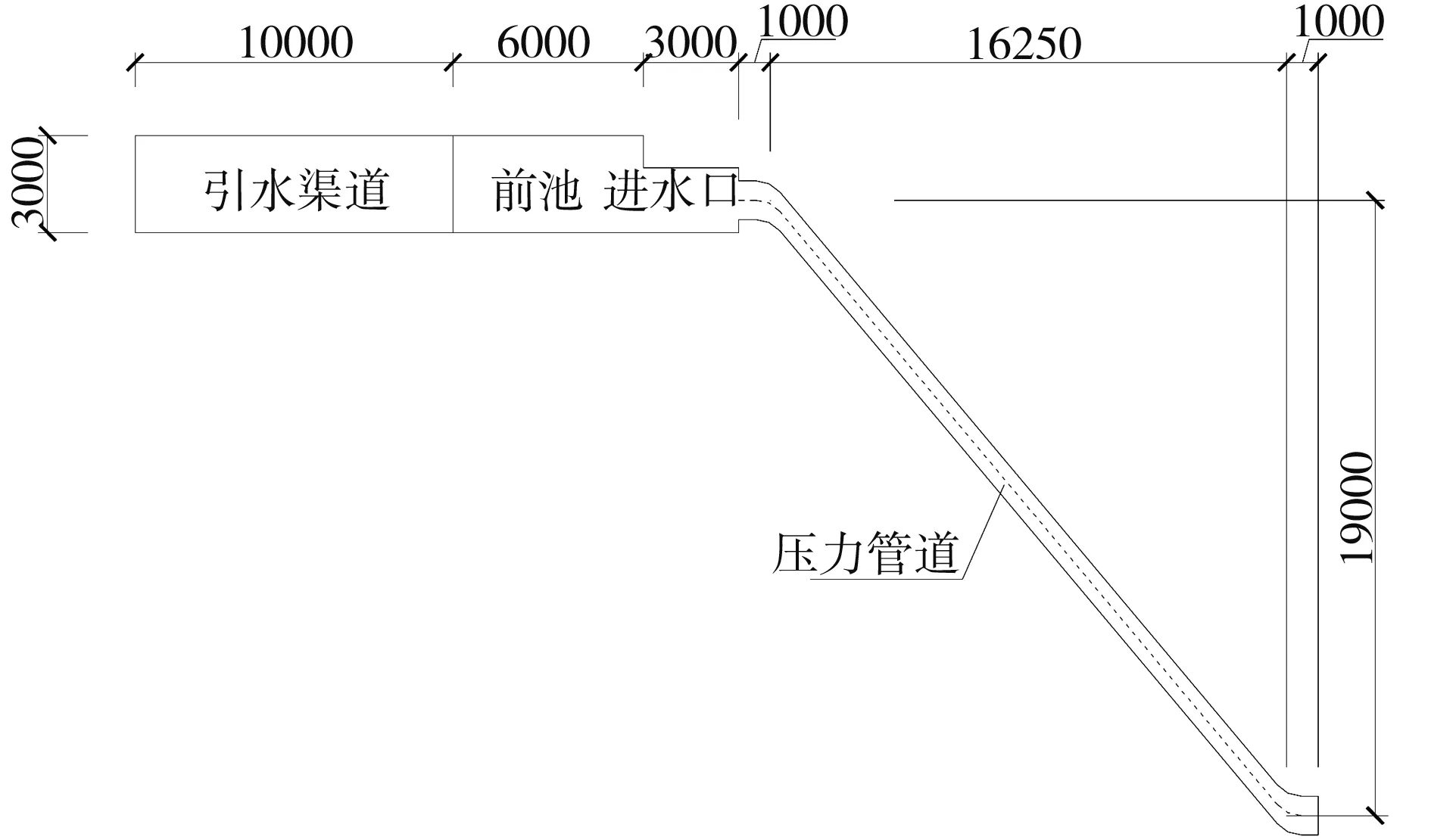
图1 小水电引水建筑物断面(单位：mm)

该工程的压力管道沿程水头损失采用海曾-威廉公式计算，混凝土钢管海曾-威廉粗糙系数Cw取为120，额定流量Q=2.8m3/s时，压力管道沿程水头损失为

(14)

压力管道渐变处局部水头损失采用公式(13)计算，局部水头损失系数λ取0.25，额定流量Q=2.8m3/s时，渐变处局部水头损失为

(15)

为了探索不同流量工况下压力管道局部水头损失与沿程水头损失的变化，图2给出了1.2m3/s、1.6m3/s、2.0m3/s、2.4m3/s、2.8m3/s、3.2m3/s六种流量下的压力管道水头损失值。从图2可看出：压力管道沿程水头损失与局部水头损失均随流量变大而变大，在相同流量工况下，压力管道沿程水头损失较局部水头损失更大。

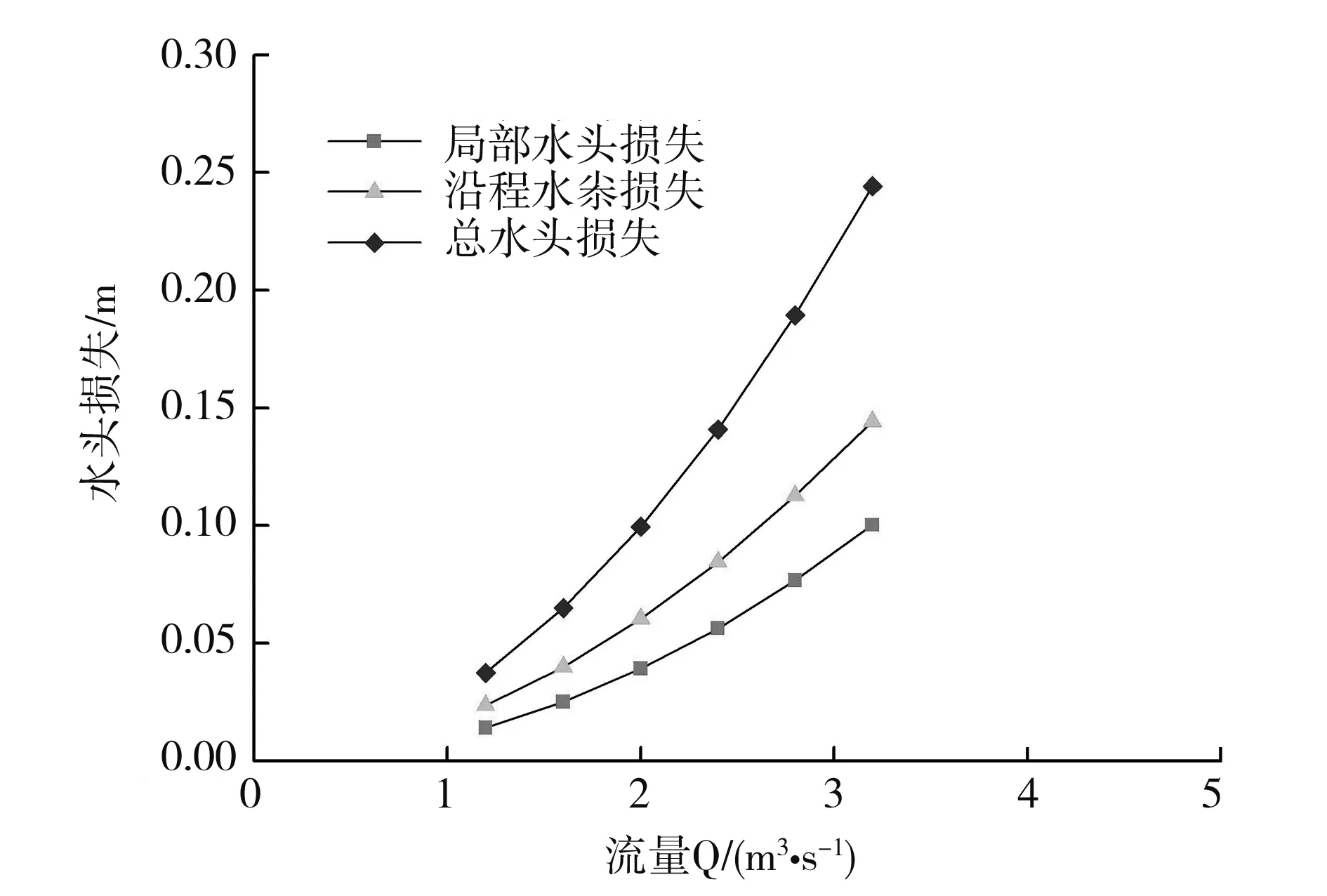
图2 不同流量下的压力管道水头损失

管道糙率是压力管道产生沿程水头损失的直接原因，现有技术只是尽量减小管道材质的糙率，从而尽可能减少管道沿程水头损失。取引水渠道进水口横断面和压力管道出口断面为计算断面，定义管道出口中心水平面为基准面，动能修正系数取1.05，将水头损失计算结果代入伯努利方程(1)，可得压力管道出口压强理论计算值。不同流量压力管道出口压强理论计算结果如表1所示，由表可见引水建筑物总水头损失随流量变大而变大，而压力管道出口压强值随流量变大而减小，压力管道出口压强与总水头损失负相关。

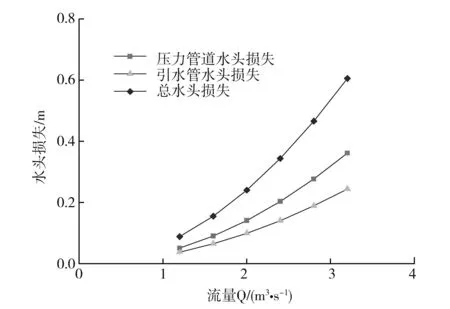
图3 进水口压力管道水头损失理论计算值

引水建筑物中进水口与压力管道连续紧密，将进水口压力管道作为整体计算域进行计算，其结果如表2所示，依据该表可汇制如图3所示的关系曲线。从图3可看出：进水口水头损失较压力管道水头损失大很多，这是由于进水口附近由于边界条件发生剧烈变化，导致水流形态高度紊乱，进水口水头损失较大的缘故。进水口水头损失与压力管道水头水头损失均随流量的增加而增加，在相同流量下压力管道水头损失小于进水口水头损失，且随着流量增加压力管道水头损失变化较进水口水头损失更为平缓。

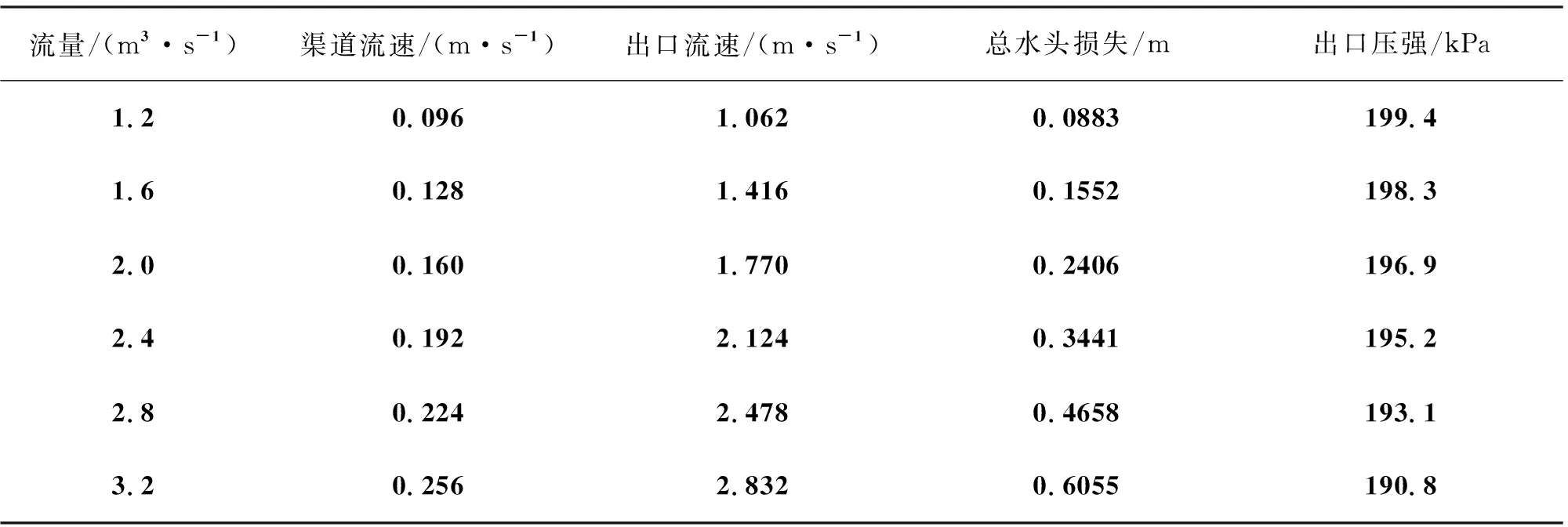
表1 压力管道出口压强理论计算值

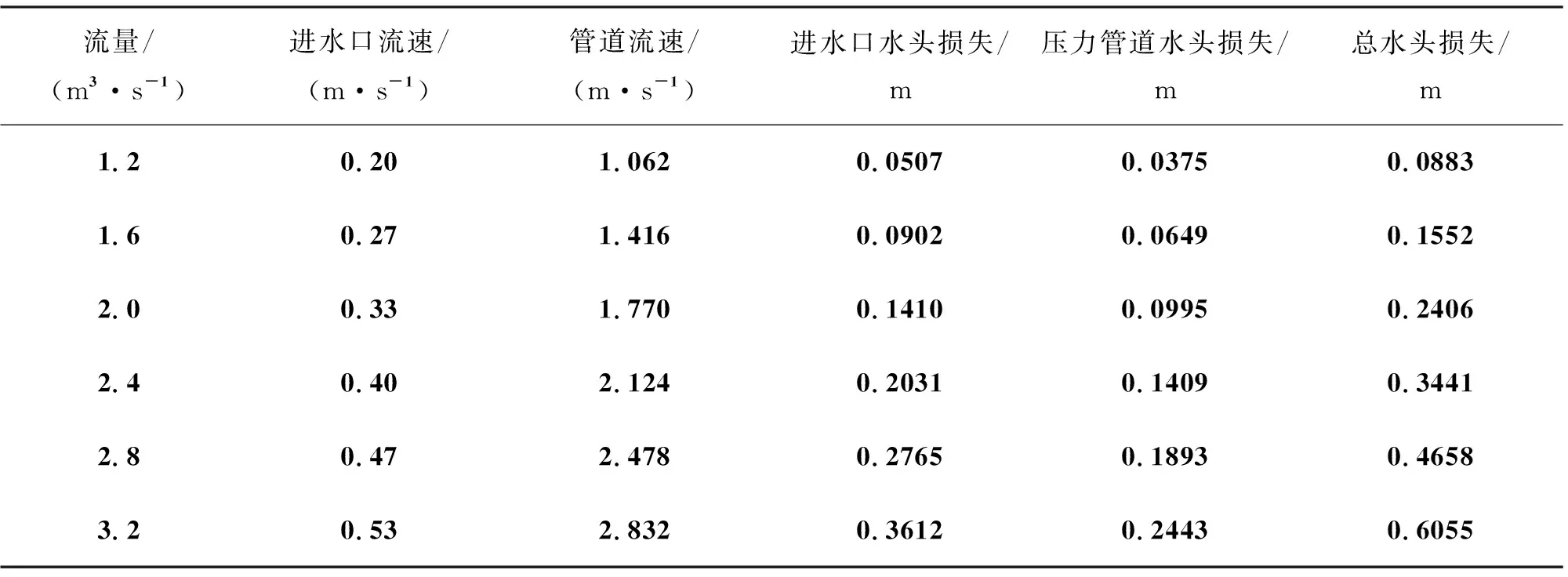
表2 进水口压力管道水头损失理论计算值

压力管道的水头损失随管道流量的增加而增大，因此，农村小水电压力管道的过水流量并非越大越好，需根据水电站实际需求确定。

3 结 语

本文依据恒定总流伯努力方程中沿程水头损失与局部损失计算公式，对小水电站的压力管道进行水头损失计算，得到如下认识：压力管道水头损失包括沿程水头损失与局部水头损失两部分，其中沿程水头损失发生在整个管道壁面上，局部水头损失主要发生在压力管道渐变段处；压力管道沿程水头损失与局部水头损失均随流量变大而变大，相同流量工况下压力管道沿程水头损失较局部水头损失更大。