考虑非线性摩擦的电动伺服缸加载系统鲁棒自适应控制

李辉 杨绿 吴怀超

摘要：非线性摩擦、外界扰动以及参数不确定性对电动伺服缸加载系统加载精度和响应特性带来不利影响。针对该问题，引入LuGre非线性摩擦模型，建立了电动伺服加载系统动力学模型，将非线性摩擦纳入系统总扰动中，设计了一种鲁棒自适应控制器（ARC）;应用Lyapunov稳定性理论证明了所设计的鲁棒自适应控制器的稳定性。经仿真表明，相较于传统PD控制器，本文所设计的ARC控制器能使电动伺服缸加载系统具有更优的加载力跟踪精度和良好的鲁棒性。

关键词：鲁棒自适应;电动伺服缸;非线性摩擦

中图分类号：TP273.2;TP271.2

文献标识码： A

相较于砝码和液压伺服加载，电动伺服缸可动态加载，

具有传动机构简单、系统稳定高效以及加载精度高等特点，越来越多地应用于高精度动态加载系统中，但其伸缩活塞与缸体的非线性摩擦特性、外部干扰和参数不确定性对电动伺服缸加载精度和动态响应特性影响较大。因此，电动伺服缸控制器设计中，有必要纳入上述非线性摩擦特性和参数不确定性因素以保证加载精度、跟随效果和稳定性。

近年来，随着动态加载精度的要求越来越高，电动伺服缸控制器设计引起了不少研究者的关注。如，秦幸妮等[1]将自抗扰技术应用到电动伺服缸中，设计了系统位置环的自抗扰控制器。结果表明，自抗扰控制器控制的电动伺服缸定位精度高。此外，为满足电动缸位移与力的伺服控制需求，张爱龙等[2]提出了带前馈的PD闭环控制器，该控制方法具有较好的力和位移跟踪效果。针对伺服系统中存在的非线性扰动问题，龙力军[3]提出了一种自适应控制器，该控制器解决了系统未知扰动参数估计问题，但未考虑系统非线性摩擦问题。为了进一步补偿电动伺服缸非线性摩擦问题，山显雷等[4]基于LuGre摩擦模型和PD控制算法，设计了摩擦补偿控制器，提高了位置跟踪精度，但该研究未考虑外部扰动和系统参数不确定性问题。

针对上述问题，本文设计了系统的自适应律，实现系统未知参数的在线估计，并借助自适应控制器对外部总体干扰进行补偿。通过仿真验证所提鲁棒自适应控制器的加载力跟踪精度和动态响应特性。

1电动伺服缸加载系统动力学模型

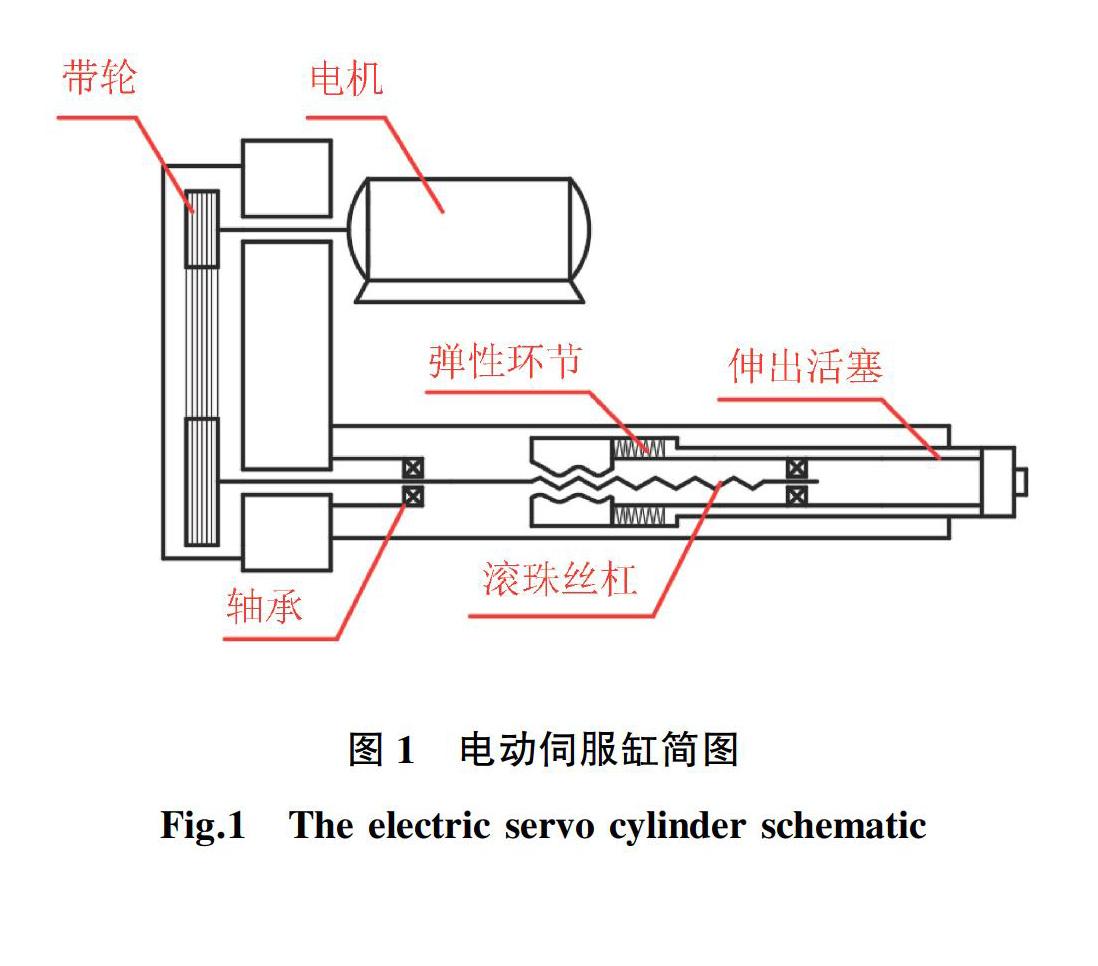
电动伺服缸加载系统结构如图1所示，其传动系统由伺服电机、减速带、轴承、滚珠丝杠、弹簧等元件组成。

2鲁棒自适应设计

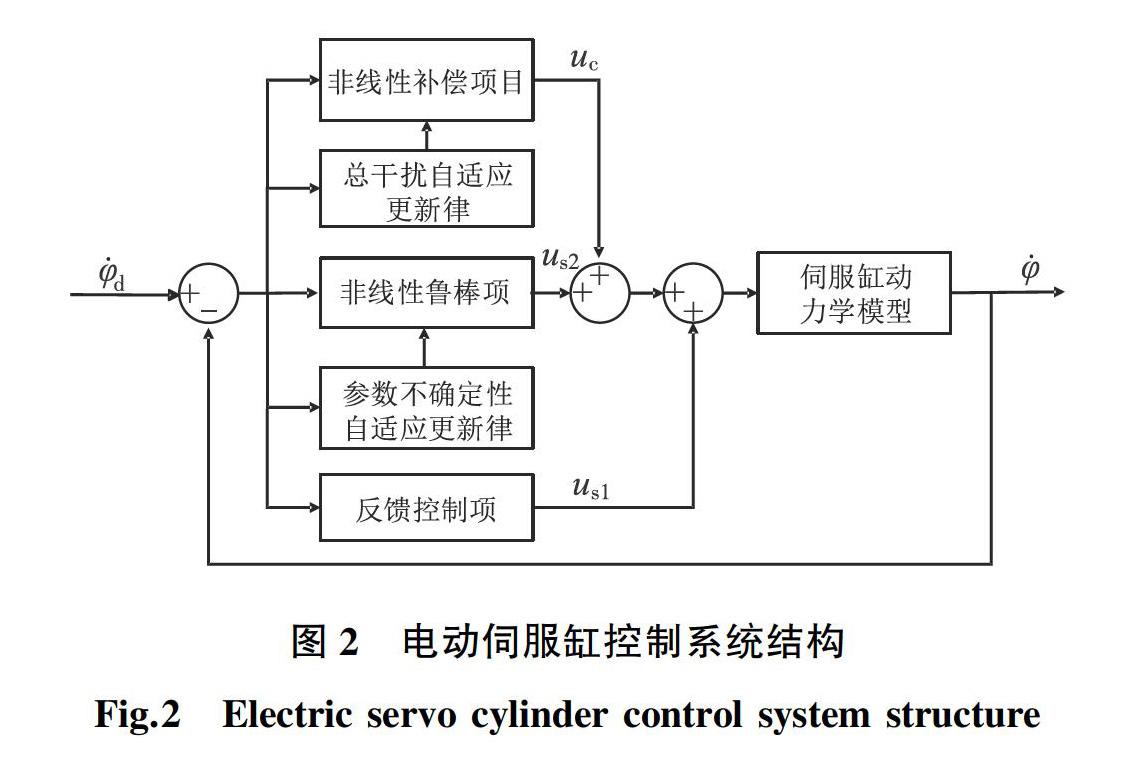
整个电动伺服缸加载系统中主要包含了非线性摩擦、参数不确定性和外界扰动等特性，因此采用鲁棒自适应控制器，整个电动伺服缸控制系统的结构框图如图2所示。

3仿真结果与分析

输入期望加载力F=3/πsin（t）的正弦信号，仿真时间设置30 s，加载力跟踪仿真结果如图3所示，从图中可以看出，控制系统可在0.4 s内完成跟随。图4是ARC控制加载力跟随误差与传统的PD控制跟踪误差对比图，从图中得出鲁棒自适应控制的稳定性更好、跟踪效果更优。

图5为外加功率为0.001，采样时间为0.1 s的白噪声干扰下的仿真图，从图5可以看出，在外加干扰条件下，ARC控制相比PD控制的加载力跟踪效果更好，误差幅值下降了60%左右。同时，为验证变载荷跟随效果，分别给定不同的加载力：3 N、4 N、6 N，仿真时间为3 s，如图6所示，系统在0.4 s内也可以完成变信号下的快速跟踪。

4结论

本文针对电动伺服缸非线性摩擦特性、外部扰动以及参数不确定性对伺服精度和动态特性的影响，设计了一种鲁棒自适应控制器，该控制器通过将非线性摩擦纳入外部扰动进行补偿。经Lyapunov理论证明，所提控制器可以在有限时间内快速收敛到平衡点附近的邻域内;此外，经仿真验证，鲁棒自适应控制能很好地跟随期望加载力，在外部干扰作用下，也能在有限时间内快速收敛到平衡点附近的邻域内;与传统的PD控制器相比，鲁棒自适应控制器的稳定性和加载力跟随效果更优。

参考文献：

[1]

秦幸妮， 姜明， 刘彦艳，等. 自抗扰控制技术在电动缸伺服系统中的研究[J]. 火炮发射与控制学报， 2019，40（1）：49-52.

[2]张爱龙， 喻镇涛， 伊斯武， 等. 基于cRIO平台的电动缸位移与力伺服控制系统设计[J]. 电气传动， 2019，49（4）：91-94.

[3]LONG L J . Robust Adaptive Control for Switched Nonlinearly Parameterized Systems with Dynamic Uncertainties[J].IEEE International Journal of Control， 2019，25（3）：1-19.

[4]山顯雷，程刚，刘后广.基于摩擦模型的电动缸PID摩擦补偿控制研究[J].组合机床与自动化加工技术， 2013，47（8）：66-68.

[5]张相进. 新型电动加载器设计及其动态特性分析[D].秦皇岛：燕山大学，2017.

[6]JIN W， NI A L， JIAN L C， et al. Adaptive control of servo system based on LuGre model[J]. IOP Conference Series Materials Science and Engineering， 2018，52（11）：75-79.

[7]胡庆雷，李波，张爱华，等.考虑推力器安装偏差的航天器姿态机动有限时间控制[J].控制理论与应用，2013，74（4）：417-424.

[8]王璐，郭毓，姚伟，等.带有摩擦非线性的CMG框架伺服系统有限时间自适应鲁棒控制[J].控制与决策，2019，34（4）：885-890.

[9]杜仁慧，吴益飞，陈威，等.考虑LuGre摩擦的伺服系统自适应模糊控制[J]. 控制与决策， 2013，56（8）：1253-1256.

[10]杨嘉伟 基于自抗扰和分数阶PD控制的永磁同步电机伺服控制策略研究[D].北京：北京理工大学，2015.

[11]ZHAO R， CHEN Y H， JIAO S， et al. A constraint￣following control for uncertain mechanical systems： given force coupled with constraint force[J]. Nonlinear Dynamics， 2018， 93（3）：1-17.

[12]王璐，郭毓，钟晨星，等.控制力矩陀螺框架伺服系统期望补偿自适应鲁棒控制[J].控制理论与应用，2017，34（9）：1143-1150.

[13]LI P， JIA X， FENG J， et al. Prognosability study of ball screw degradation using systematic methodology[J]. Mechanical Systems and Signal Processing， 2018，109（5）：45-57.

[14]CHEN Q， REN X， NA J， et al. Adaptive robust finite￣time neural control of uncertain PMSM servo system with nonlinear dead zone[J]. Neural Computing and Applications，2017， 28（12）：3725-3736.

[15]RUDPOSHT M K， NEKOUI M A， TESHNEHLAB M . Robust optimal control for a class of nonlinear systems with uncertainties and external disturbances based on SDRE[J]. Cogent Engineering，2018，46（5）：1-16.

（責任编辑：周晓南）