考虑动态吸收率的玻璃温室覆盖层温度预测模型
张观山,李天华,侯加林
·农业生物环境与能源工程·
考虑动态吸收率的玻璃温室覆盖层温度预测模型
张观山,李天华,侯加林※
(1. 山东农业大学机械与电子工程学院,泰安 271018;2. 山东省农业装备智能化工程实验室,泰安 271018)
覆盖层温度是影响温室热环境的重要因素之一。为了实现温室覆盖层温度预测,该研究以玻璃温室覆盖层为研究对象,综合考虑太阳辐射吸收、对流换热等能量传递形式,建立温室覆盖层温度预测模型。为提高模型精度,该研究进一步提出温室覆盖层动态吸收率计算方法,并使用该方法将覆盖层太阳辐射吸收率分为直射辐射吸收率、散射辐射吸收率与地表反射辐射吸收率分别计算,进而精确计算覆盖层吸收太阳辐射。为验证模型正确性及其精度,在山东省泰安市选择3个时段开展相关验证试验并得出如下结论,温室覆盖层温度预测值与测量值变化趋势较为一致,模型计算值与覆盖层温度测量值的决定系数2最小为0.92,均方根误差RMSE最大为2.05 ℃,通过与相关模型对比得出该研究提出的模型能够精确预测覆盖层温度。
温度;模型;温室;覆盖层;动态吸收率;太阳辐射;能量传递
0 引 言
近年来,中国引进诸多荷兰纹络型玻璃温室,这些温室全部配备荷兰先进的环境管理系统,但由于运营成本高等问题,导致大部分乃至所有玻璃温室的运营处于亏损状态。究其原因,中国气候与荷兰气候差异大,玻璃温室需在中国冬季和夏季分别增加大量的能耗用以加热和降温,从而维持作物适宜的生长环境,其原有环境管理系统不再适用。因此,针对中国气候特点,研究如何降低玻璃温室能耗,提高玻璃温室能源管理水平至关重要。
降低温室能耗需精确评估温室能耗需求[1-2],精确评估温室能耗需求需全面掌握温室内部能量传递规律[3-4]。温室内部能量传递是一个复杂的非线性系统[5]且受多个因素影响,其中覆盖层温度是影响温室内部能量传递及温室内热环境的重要因素之一[6]。覆盖层通过对流换热与温室内空气交换热量进而影响室内空气温度。覆盖层通过长波辐射与土壤交换热量影响土壤温度,进而对作物根系温度、土壤蒸散等产生间接影响。覆盖层与作物通过长波辐射影响作物温度,进而对作物呼吸作用、蒸腾作用产生间接的影响。覆盖层温度是计算以上能量交换的重要变量,并对以上能量交换过程具有决定作用,因此有必要准确获取覆盖层温度。
覆盖层温度可通过传感器测量或模型预测的方法获取。传感器测量方法主要有红外线传感器测量和热电偶测量两种方式,然而红外线温度传感器测量方式在高温时误差较大[7],热电偶测量方式会因太阳辐射、热辐射和空气流动影响而产生误差[8]。此外,Molina-Aiz等[9]提出使用防辐射罩遮挡热电偶的方式测量覆盖层温度,但是该方式因热电偶与防辐射罩之间间隙累积传感器生成的热量而产生测量误差。
在覆盖层温度模型预测方面,诸多专家学者在研究温室能量平衡模型的同时,也对覆盖层温度预测进行了研究。Abdul-Ghany等[10]开发了温室能量平衡模型并在自然通风、喷洒降温情况下对温室内部的微气候包括覆盖层温度进行预测。Reyes-Rosas等[11]对自然通风状况下的温室建立能量平衡模型,该模型使用不同热量传递系数描述顶窗通风与侧窗通风对温室内热环境的影响并实现覆盖层温度预测。Mobtaker等[12]对位于伊朗西北部的温室建立能量平衡模型并对温室覆盖层温度进行预测,模型假设覆盖层太阳辐射吸收率为0.1。Singh等[13]根据质量和热量平衡原理对自然通风状况下种植有黄瓜的温室建立了温室微气候模型,该模型使用SIMULINK求解并计算得出覆盖层温度。中国大部分研究针对日光温室[14-18],鲜有针对玻璃温室覆盖层温度测量及预测研究的相关报道。
总结前述文献可发现,在覆盖层温度预测模型的构建方面存在诸多不足,具体如下:
1)鲜有研究考虑覆盖层吸收太阳辐射或将覆盖层太阳辐射吸收率设定为固定值。虽然覆盖层太阳辐射吸收率较小,但如果不考虑覆盖层吸收太阳辐射,则随着时间的推移,所忽略的覆盖层吸收太阳辐射会越累积越大,以至于在评估覆盖层温度时误差越来越大。如果将覆盖层太阳辐射吸收率设定为固定值,覆盖层温度预测误差可能会小于忽略覆盖层吸收率所产生的误差,但将覆盖层太阳辐射吸收率设定为固定值仍不能真实反映覆盖层太阳辐射吸收率的真实变化规律。温室覆盖层太阳辐射吸收率是由太阳入射角、覆盖层折射系数、消光系数等因素决定且随时间动态变化[19]。同样,随着时间的推移,因将覆盖层太阳辐射吸收率设定为固定值造成覆盖层吸收太阳辐射的累积误差不断增大,进而影响了覆盖层温度评估和温室环境控制精度。综上,忽略温室覆盖层吸收太阳辐射或将覆盖层太阳辐射吸收率设定为固定值会在预测覆盖层温度时产生较大误差,有必要研究温室覆盖层太阳辐射动态吸收率计算方法,并将该方法应用于温室覆盖层温度评估以及温室环境控制系统开发,以提高温室环境控制精度。
2)多数模型验证试验期间室内外环境变化幅度较小且试验周期较短。室内外环境变化幅度越大,试验周期越长,模型精度越低[11]。只有模型在温室内外环境变化幅度大且试验周期长的情况下具有较高精度,才能充分说明模型精度符合要求。
3)大部分研究仅将温室屋顶作为覆盖层进行研究,而没有考虑四周墙体对温室热环境的影响。即使部分研究考虑了四周墙体对温室热环境的影响,但是这些研究假定温室不同覆盖面(屋顶,四周墙体)温度相同。实际上,温室不同覆盖面温度有一定差异(中午及夜间差异较大),将温室不同覆盖面温度按照相同温度处理会在预测温室内热环境时产生较大误差,因此有必要将温室不同覆盖面温度分别计算以提高温室热环境预测精度。
针对上述问题,本研究建立温室覆盖层温度预测模型,提出了温室覆盖层太阳辐射动态吸收率计算方法,并根据该方法将覆盖层太阳辐射吸收率分为直射辐射吸收率、散射辐射吸收率与地表反射辐射吸收率分别计算,进而精确计算覆盖层吸收太阳辐射以提高覆盖层温度预测精度。为了验证模型正确性及精度,本研究分别选择冬季寒冷(无作物)、夏季炎热(无作物)以及秋季(有作物)3种温室环境开展模型验证试验,每种情况试验周期10 d,总试验周期30 d。模型验证试验期间室内外环境变化幅度大,试验周期长,以验证模型具有较大的适用范围。
1 材料与方法
1.1 试验温室
试验地点位于山东省泰安市夏张镇(36°08'N,116°95'E),试验对象为玻璃温室(图1)。温室为南北朝向,长度5 m,宽度3 m,檐高2.05 m,脊高3 m,屋顶倾角26°。屋顶使用单层钢化玻璃,厚度8 mm,温室四周墙体使用单层钢化玻璃,厚度6 mm。

图1 温室能量传递及温度传感器布局侧视图
1.2 温室环境监测
温室环境监测选用武汉汉秦信通科技有限公司生产的HQZDZ型数据采集器,数据采集时间分别为2019年1月26日—2019年2月4日,2019年7月11日—2019年7月20日,2019年10月14日—2019年10月23日,采集的数据包括室内空气温度、覆盖层温度、土壤表层温度、作物温度、室外大气温度、室外太阳辐射照度、室外风速等。以上数据每5 min采集一次并通过GPRS传送到远程服务器,远程服务器使用SQL Server数据库存储数据。温室环境监测传感器技术参数如下:
1)室内空气温度和室外空气温度选择相同型号传感器测量,传感器型号为HQWD,精度±0.3 ℃,测量范围−50~100 ℃。
2)覆盖层温度测量选用贴片温度传感器,型号为HQTPW,精度±0.3 ℃,测量范围−50~100 ℃。温室南北屋顶内外表面及四周墙体内外表面分别布置贴片温度传感器,并将不同覆盖面内外表面贴片温度传感器测量数据平均值分别作为不同覆盖面温度测量值。贴片温度传感器使用导热系数为2.0 W/(m∙K)的导热硅胶覆盖,以消除太阳辐射、热辐射以及空气流动对测量精度的影响,同时也避免了使用防辐射罩产生传感器累积热量而造成的误差。
3)地表土壤温度传感器型号为HQTW,精度±0.5 ℃,测量范围−50~80 ℃。
4)太阳辐射照度传感器型号为HQTBQ,测量精度1 W/m2,测量范围0~2 000 W/m2。
5)作物温度使用红外温度传感器测量,传感器型号为HQS111,测量精度±0.2 ℃,测量范围−50~100 ℃。
6)室外风速传感器型号为HQFS,测量精度±0.3 m/s,测量范围0~70 m/s。
2 覆盖层温度预测模型构建方法及过程
覆盖层温度的影响因素包括太阳辐射吸收、对流换热、长波辐射等能量交换形式(图1)。覆盖层吸收太阳辐射为覆盖层表面太阳辐射照度与覆盖层透射率的乘积,因此计算覆盖层吸收太阳辐射需首先分别计算覆盖层表面太阳辐射照度和覆盖层透射率。表1为模型计算过程中所涉及符号的意义、单位及取值。

表1 模型符号及数值
2.1 温室覆盖层表面太阳辐射照度计算
覆盖层吸收太阳辐射照度为覆盖层表面太阳辐射照度与覆盖层太阳辐射吸收率的乘积。计算覆盖层吸收太阳辐射照度需首先计算覆盖层表面太阳辐射照度。温室覆盖层表面太阳辐射由直射辐射、散射辐射和地表反射辐射3部分构成[20](图1),并根据水平面太阳辐射o中直射辐射和散射辐射计算[21]。水平面太阳辐射o中散射辐射比例dif由式(1)确定[22]
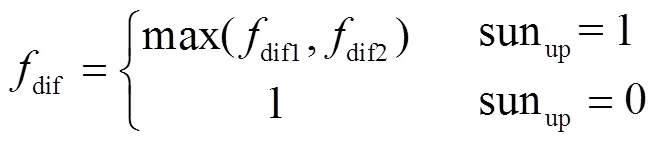
式中太阳升起时sunup=1,其余时间sunup=0;dif1与dif2为计算散射辐射比例dif的中间变量,dif1通过式(2)确定
(2)
dif2则通过式(3)确定

sin为太阳高度角的余弦

atm为大气透明度,通过式(5)确定[21]
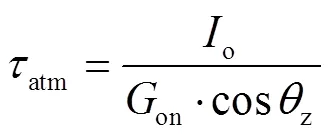
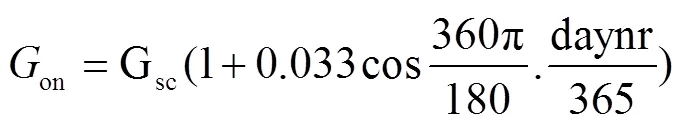
式中Gsc为太阳常数[19],W/m2,取常数值1 367;daynr为日期序号,例如1月1日,则daynr=1;z为太阳方位角,(°),通过式(7)计算[19]
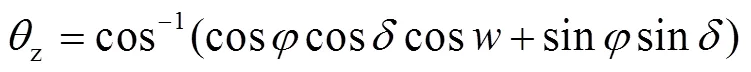
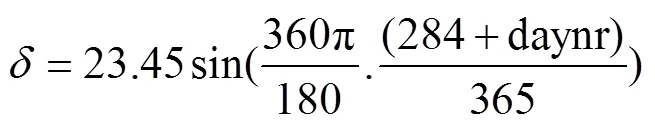
为时角[23],(°)如式(9)所示
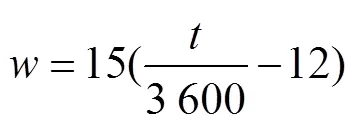
式中为时间,s。
水平面太阳辐射o的直射分量与散射分量通过式(10)和式(11)计算
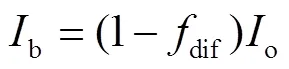
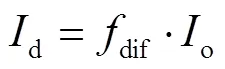
温室不同覆盖面太阳辐射照度S,W/m2,通过式(12)计算[24]
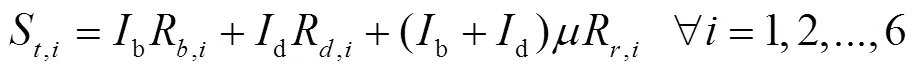

式中A为温室不同覆盖面面积,m2,根据温室实际尺寸确定;R为温室不同覆盖面直射辐射强度与水平面直射辐射强度比值,通过式(14)计算[19]

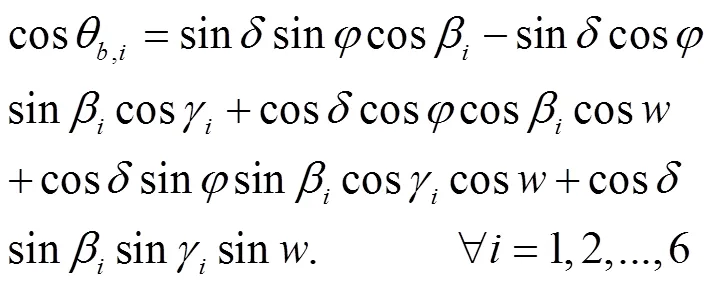
式中为温室不同覆盖面相对水平面倾角,(°);为温室不同覆盖面表面方位角,(°)。
R和R分别指温室覆盖层表面与天空和地面的视角系数,通过式(16)和式(17)计算[25]
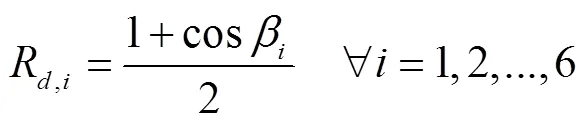
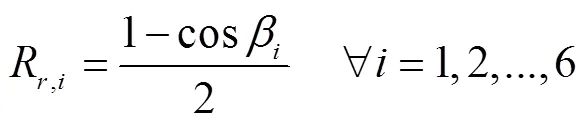
2.2 温室覆盖层太阳辐射动态吸收率计算
温室覆盖层太阳辐射吸收率具体计算过程如下[19]:
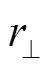

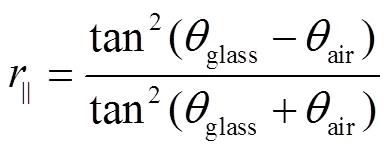
温室覆盖层反射太阳辐射为垂直分量与平行分量平均值如式(20)所示
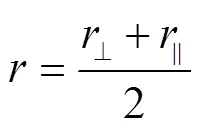
air和glass分别是光线入射角和折射角,(°),如图2所示,满足式(21)
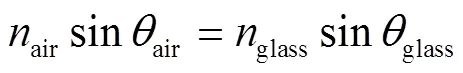
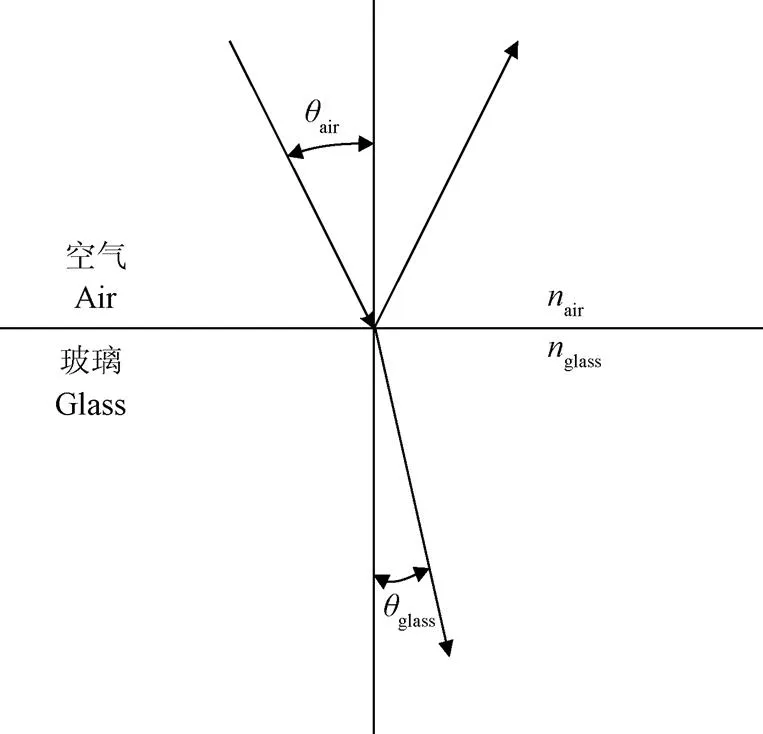
注:nair为空气折射系数;nglass为玻璃折射系数;θair为光线入射角,(°);θglass为光线折射角,(°)。
覆盖层吸收系数如式(22)所示


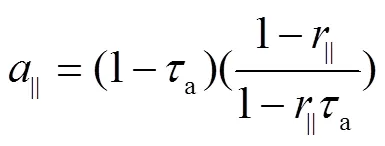
最后,温室覆盖层吸收率为入射光线垂直分量和平行分量吸收率的平均值如式(25)所示
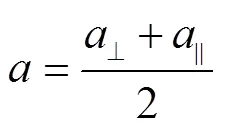
2.3 温室覆盖层吸收太阳辐射计算
因温室覆盖层表面太阳辐射由直射辐射、散射辐射、地表反射辐射构成[20],为计算覆盖层吸收太阳辐射,需分别计算覆盖层直射辐射吸收率、散射辐射吸收率和地表反射辐射吸收率。根据前述覆盖层太阳辐射动态吸收率计算方法,需首先计算覆盖层直射辐射入射角、散射辐射入射角、地表反射辐射入射角。
太阳直射辐射入射角θ通过式(15)计算,θ为散射辐射等效为相同吸收率直射辐射对应太阳入射角,通过式(26)计算[19]
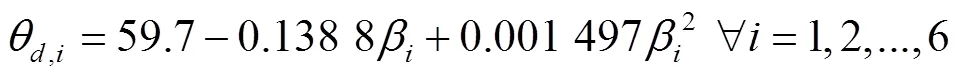
θ,j为地表反射辐射等效为相同吸收率直射辐射对应太阳入射角,通过式(27)计算[19]
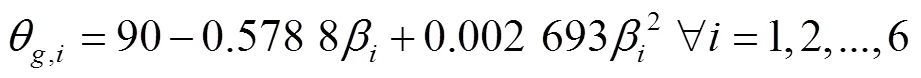
温室不同覆盖面单位面积吸收太阳辐射瞬时值通过式(28)计算[24]

2.4 温室覆盖层能量平衡方程
综合考虑温室不同覆盖面(南屋顶、北屋顶、南墙、北墙、东墙、西墙)太阳辐射吸收、对流换热、长波辐射等能量传递形式(图1),以温室不同覆盖面为对象,分别建立能量平衡方程(29)

式中c为覆盖层密度,kg/m3;p,c为覆盖层比热容,J/(kg·K);V,i为不同覆盖面体积,m3;T,i为不同覆盖面温度,K;C,i为不同覆盖面吸收太阳辐射,W,通过式(28)计算。
Q,i为室内空气与不同覆盖面对流换热交换热量,W,通过式(30)计算[21]
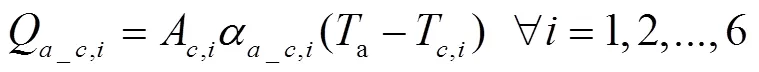
式中A,i为不同覆盖面面积,m2;a为室内空气温度,K;,i为室内空气与不同覆盖面内表面对流换热系数,通过式(31)计算[21]
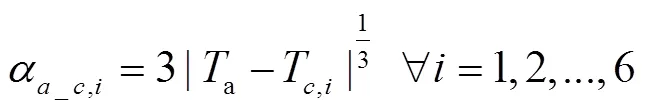
Q,i为温室覆盖层与室外空气对流换热交换热量,W,通过式(32)计算[26]
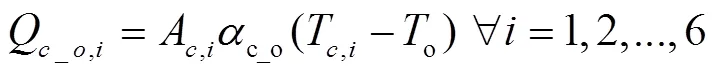
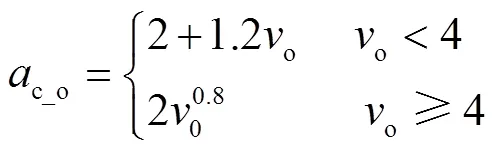
式中o为室外风速,m/s。

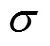
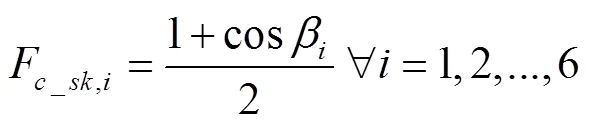
式中sky为天空温度,K,通过式(36)计算[27]
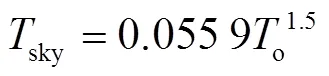
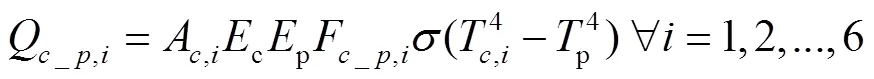

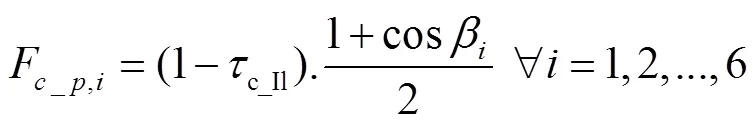

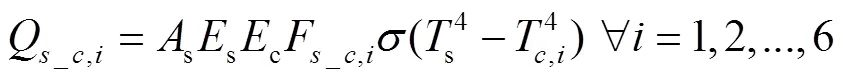
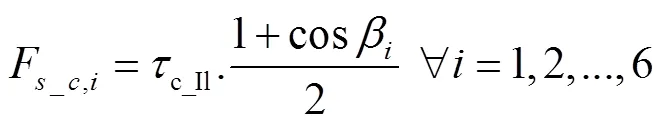
2.5 覆盖层温度预测模型求解
模型输入为室外大气温度、室外风速、室外太阳辐射照度、室内空气温度、地表温度、作物温度以及温室尺寸(表1)等数据,模型输出为覆盖层温度。模型使用龙格库塔四阶积分求解算法以及MATLAB提供的常微分方程数值求解函数ode45进行求解,步长设置为5 min。
3 结果与分析
3.1 室内外气象条件
本研究通过对比3个试验阶段(1月26日—2月4日,7月11日—7月20日,10月14日—10月23日)覆盖层温度预测模型计算值与覆盖层温度测量值验证模型精度。前2个阶段温室内未种植作物且未采取任何加热、降温措施,第3个试验阶段温室内种植西红柿。以上3个试验阶段分别代表冬季寒冷、夏季炎热以及秋季种植作物的情况。图3为试验期间太阳辐射照度变化曲线。图4为试验期间室外空气温度、室内空气温度、室内地表温度变化曲线。表2为试验期间室内外环境数据最大值、最小值、平均值统计结果。
第1个试验阶段太阳辐射照度日最大值变化范围为191~647 W/m2,第2个试验阶段太阳辐射照度日最大值变化范围为892~1 036 W/m2,第3个试验阶段太阳辐射照度日最大值变化范围为285~803 W/m2。从表2得出,室外最高空气温度为37.3 ℃,室外最低空气温度为−12.3 ℃,室外空气温度变化幅度为49.6 ℃。室内空气温度最高为66.5 ℃,室内空气温度最低为−9.1 ℃,室内空气温度变化幅度为75.6 ℃。室内地表温度最高为46.4 ℃,室内地表温度最低为0.6 ℃,室内地表温度变化幅度为45.8 ℃。
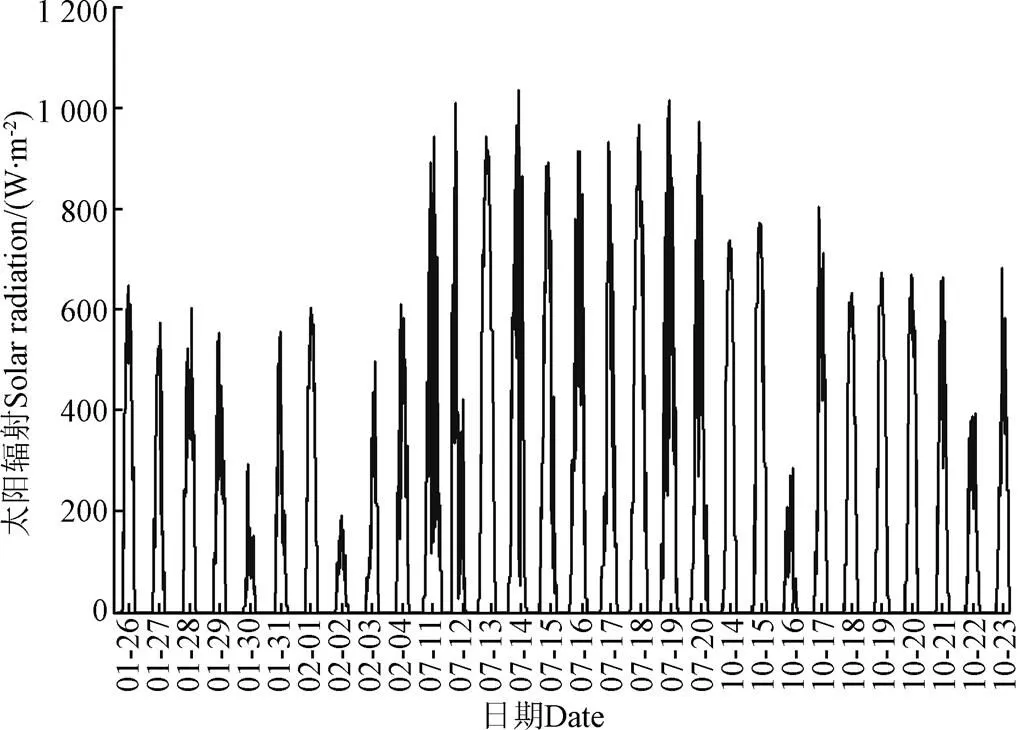
图3 2019年3个试验阶段太阳辐射照度变化曲线

图4 2019年3个试验阶段室内空气温度、室外空气温度、室内地表温度曲线
本研究取不同覆盖面内外表面贴片温度传感器测量数据平均值分别作为不同覆盖面温度测量值,不同覆盖面温度测量值与模型计算值比较以确定模型精度。第1个试验阶段不同覆盖面温度测量值与不同覆盖面内外表面温度的平均偏差(mean bias error, MBE)变化范围为0.66~0.92 ℃。第2个试验阶段不同覆盖面温度测量值与不同覆盖面内外表面温度的平均偏差MBE变化范围为1.15~1.40 ℃。第3个试验阶段不同覆盖面温度测量值与不同覆盖面内外表面温度平均偏差MBE变化范围为0.61~0.81 ℃。以上数据说明不同覆盖面温度测量值与不同覆盖面内外表面温度偏差较小。
本研究提出的覆盖层太阳辐射动态吸收率计算方法没有验证其正确性的直接方法,只能通过验证考虑动态吸收率玻璃温室覆盖层温度预测模型精度的方式间接判定该方法是否正确。只要考虑覆盖层动态吸收率的玻璃温室覆盖层温度预测模型正确且覆盖层温度预测精度进一步提高,则说明本研究所提出的覆盖层太阳辐射动态吸收率计算方法可行。温室覆盖层温度受室内外环境(室外太阳辐射照度、室外空气温度、室内空气温度等)影响,室内外环境变化幅度越大,试验周期越长,模型精度越低[11]。因此为了更充分的验证模型的精度,本研究不仅在太阳辐射变化幅度较大的情况下对模型进行验证,还在室内外空气温度变化幅度较大的情况下对模型进行了验证。

表2 温室环境数据最大值、最小值和平均值
注:阶段1为2019年1月26日—2019年2月4日,阶段2为2019年7月11日—7月20日,阶段3为2019年10月14日—2019年10月23日。
Note: Stage 1 was from Jan 26, 2019 to Feb 4, 2019; stage 2 was from Jul 11, 2019 to Jul 20, 2019; stage 3 was from Oct 14, 2019 to Oct 23, 2019.
3.2 模型验证结果与分析
图5为第3个试验阶段温室不同覆盖面(屋顶、墙体)温度计算值与测量值的对比结果。表3为3个试验阶段考虑覆盖层动态吸收率与不考虑覆盖层吸收率2种情况下模型精度对比统计结果。
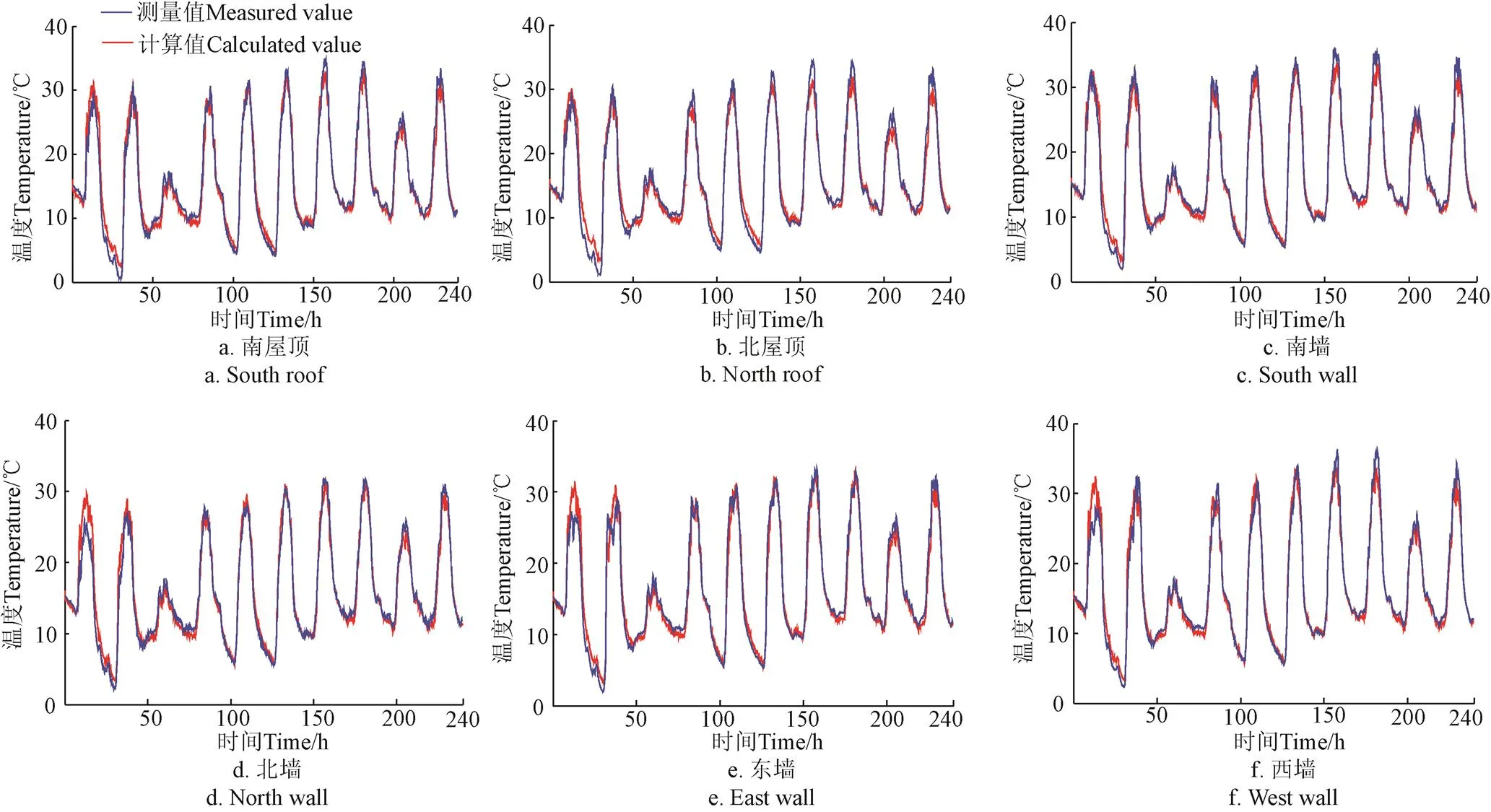
图5 第3个试验阶段温室不同覆盖面温度计算值与测量值对比曲线
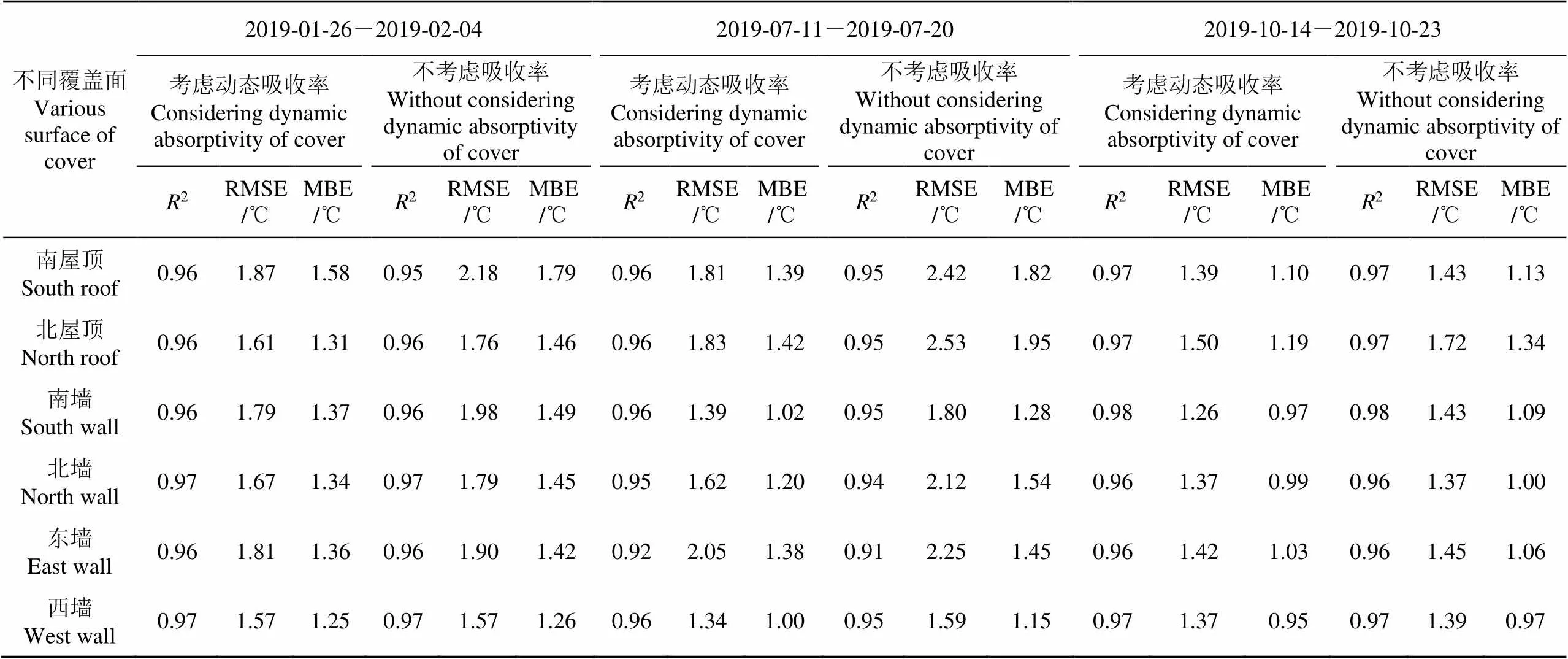
表3 考虑或不考虑覆盖层吸收率两种情况下模型精度对比
图5结果显示,温室不同覆盖面温度测量值与计算值变化趋势、最大值、最小值较为一致。模型在中午、夜间以及阴天(10月16日)预测值与测量值偏差较大。原因是覆盖层温度除了受太阳辐射影响外,还受覆盖层与天空温度的长波辐射、覆盖层与空气的对流换热等因素影响,而长波辐射、对流换热系数以及天空温度等依据经验公式确定[28]。除此之外,温室内不同位置空气温度也有差异[29],尤其在种植有作物的情况下,作物通过蒸腾作用、呼吸作用等影响温室内空气温度分布,进而增大了温室内空气温度测量误差以及覆盖层与室内空气对流换热计算误差。这些都会导致覆盖层温度预测模型与实际覆盖层温度之间存在误差。
表3结果显示,第1个试验阶段不同覆盖面温度测量值与计算值的决定系数(coefficient of determination,2)变化范围为0.96~0.97,均方根误差(root-mean-square error, RMSE)变化范围为1.57~1.87 ℃,平均偏差MBE变化范围为1.25~1.58 ℃。第2个试验阶段不同覆盖面温度测量值与计算值的决定系数2变化范围为0.92~0.96,均方根误差RMSE变化范围1.34~2.05 ℃,平均偏差MBE变化范围为1.00~1.42 ℃。第3个试验阶段温室不同覆盖面温度测量值与计算值的决定系数2变化范围为0.96~0.98,均方根误差RMSE变化范围为1.26~1.50 ℃,平均偏差MBE变化范围为0.95~1.19 ℃。
通过对比考虑覆盖层动态吸收率与不考虑覆盖层吸收率覆盖层温度预测模型精度得出(表3),第1个试验阶段考虑动态吸收率覆盖层温度计算值与测量值的均方根误差RMSE比不考虑覆盖层吸收率最大降低了0.31 ℃,平均偏差MBE最大降低了0.21 ℃。第2个试验阶段考虑动态吸收率覆盖层温度计算值与测量值均方根误差RMSE比不考虑覆盖层吸收率最大降低了0.7 ℃,平均偏差MBE最大降低了0.53 ℃。第3个试验阶段考虑动态吸收率覆盖层温度计算值与测量值均方根误差RMSE比不考虑覆盖层吸收率最大降低了0.22 ℃,平均偏差MBE最大降低了0.15 ℃。通过对比发现考虑覆盖层动态吸收率进一步提高了覆盖层温度预测模型精度。
此外,本研究使用室内外空气温度、作物温度、土壤温度等参数测量值计算长波辐射、对流换热等交换热量对覆盖层温度进行了一定修正。温室模型中,空气温度、作物温度、土壤温度等参数全部为计算值,则考虑覆盖层动态吸收率对温室模型精度提升效果会更加明显。
3.3 与相关模型对比
Baptista等[30]在葡萄牙开展了温室模型相关研究并对温室覆盖层温度进行预测,该模型未考虑覆盖层吸收太阳辐射,模型在室内空气温度变化范围为15~25 ℃情况下进行试验验证,通过计算得出覆盖层温度预测值与测量值均方根误差为1.6 ℃。虽然该模型精度与本研究所开发模型精度相近,但以上模型精度验证试验期间室内空气温度变化幅度远小于本试验(−9.1~66.5 ℃)。Singh 等[31]开发的MICGREEN模型,该模型未考虑覆盖层动态吸收率,仅将覆盖层太阳辐射吸收率设定为固定值0.20。模型在室内空气温度变化范围14~28 ℃的情况下对温室覆盖层温度进行预测,覆盖层温度预测值与测量值均方根误差为3.91 ℃。Taki等[27]建立了温室数学模型并对温室覆盖层温度预测精度进行了试验研究,该模型没有考虑太阳入射角与覆盖层太阳辐射吸收率的关系,仅假设覆盖层太阳辐射吸收率为0.017 3。模型验证试验在室内空气温度20~40 ℃范围下进行,覆盖层温度测量值与模型计算值均方根误差RMSE为1.68 ℃,决定系数2=0.97。虽然该模型覆盖层温度预测精度与本研究所开发模型相近,但上述验证试验仅对比了7个小时覆盖层温度数据,且室内空气温度变化范围远小于本研究。Reyes-Rosas等[11]开发了温室能量平衡模型,并在自然通风情况下对温室覆盖层温度进行预测,该模型虽考虑了覆盖层吸收太阳辐射,但仅将覆盖层太阳辐射吸收率设定为固定值0.03,而没有考虑太阳入射角与覆盖层吸收率的关系。该模型在作物生长期选择5个非连续时段进行模型精度试验验证,此模型覆盖层温度预测值与测量值均方根误差RMSE为2.3 ℃。
通过对比相关模型精度得出本研究构建的温室覆盖层温度预测模型具有更高精度,究其原因,温室覆盖层温度预测模型采用覆盖层太阳辐射动态吸收率精确计算覆盖层吸收太阳辐射提高了模型预测精度。
3.4 温室覆盖层吸收太阳辐射分析
在充分验证温室覆盖层温度预测模型正确性及模型精度前提下,本研究根据温室覆盖层太阳辐射动态吸收率计算方法,对试验温室覆盖层吸收太阳辐射进行了计算分析。本研究通过将式(28)计算的3个时间段不同覆盖面单位面积吸收太阳辐射瞬时值积分,得到3个时间段不同覆盖面单位面积吸收太阳辐射累积值,其结果如图6所示。
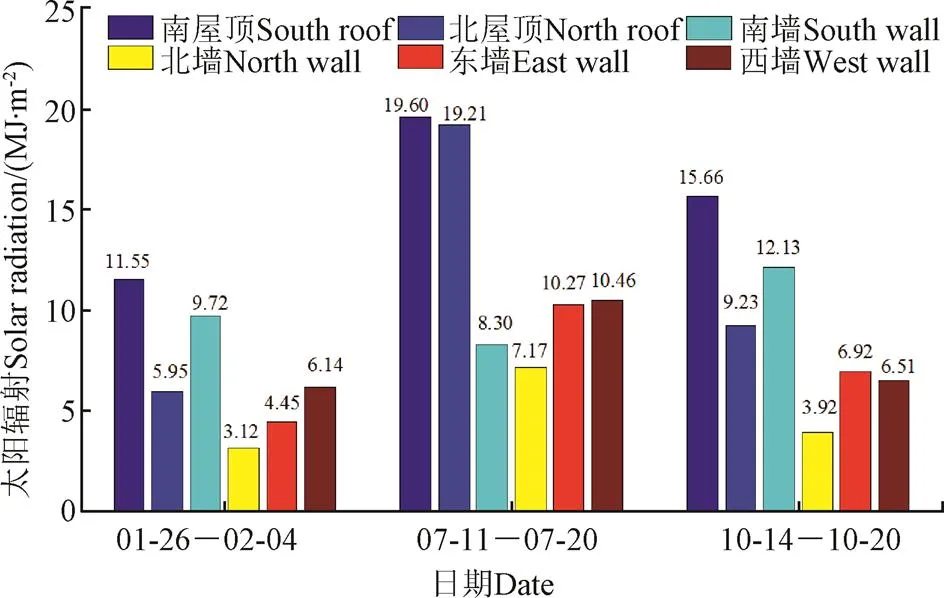
图6 温室覆盖层单位面积吸收太阳辐射
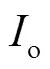
第2个试验阶段,南屋顶和北屋顶单位面积吸收太阳辐射相近且明显高于四周墙体吸收太阳辐射,同时明显高于另外2个试验阶段南屋顶和北屋顶单位面积吸收太阳辐射。南墙第2个阶段单位面积吸收太阳辐射比第1个试验阶段少1.42 MJ。其原因是夏季太阳高度角增大,温室屋顶太阳入射角减少,根据式(25),温室屋顶太阳辐射吸收率增大,且太阳辐射照度增大,因此温室屋顶吸收太阳辐射明显增加。南墙太阳入射角随太阳高度角增大而增大,根据式(25),南墙太阳辐射吸收率减小,虽然太阳辐射增强,但因南墙太阳辐射吸收率减小,南墙吸收太阳辐射减少。东墙和西墙单位面积吸收太阳辐射相近。北墙单位面积吸收太阳辐射最少(7.17 MJ/m2)。
第3个试验阶段,南屋顶和北屋顶吸收太阳辐射相比第2个试验阶段减小,且南屋顶比北屋顶单位面积多吸收了6.43 MJ太阳辐射。南墙第3个试验阶段比第2个试验阶段单位面积多吸收了3.83 MJ太阳辐射,其原因是秋季太阳高度角相比夏季降低,南墙太阳入射角减小,太阳辐射吸收率增大,南墙吸收太阳辐射增加。东墙和西墙单位面积吸收太阳辐射相近。北墙单位面积吸收太阳辐射最少(3.92 MJ/m2)。
总体来看,仅有南墙夏季单位面积吸收太阳辐射最少,其余覆盖层夏季单位面积吸收太阳辐射最多。南屋顶和北屋顶在夏季单位面积吸收太阳辐射相近,其余季节南屋顶单位面积吸收太阳辐射多于北屋顶。北墙在任何时段吸收太阳辐射都最低,原因是北墙外表面仅有散射辐射和地表反射辐射。东墙和西墙单位面积吸收太阳辐射相近,原因是太阳东升西落,上午东墙表面太阳辐射和下午西墙表面太阳辐射相近。
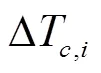

第1个试验阶段南屋顶、北屋顶、南墙、北墙、东墙和西墙每平方米分别吸收太阳辐射为11.55、5.95、9.72、3.12、4.45和6.14 MJ,通过式(42)计算,以上吸收的太阳辐射将使不同覆盖面温度分别提高687.5 、354.1 、771.4 、247.6 、353.1 和487.3 ℃。第2个试验阶段南屋顶、北屋顶、南墙、北墙、东墙和西墙每平米分别吸收太阳辐射为19.60、19.21、8.30、7.17、10.27和10.46 MJ,通过式(42)计算,以上吸收的太阳辐射将使不同覆盖面温度分别提高1 166.7 、1 143.5 、658.7 、569.0 、815.0 和830.1 ℃。第3个试验阶段南屋顶、北屋顶、南墙、北墙、东墙、西墙每平米分别吸收的太阳辐射为15.66、9.23、12.13、3.92、6.92和6.51 MJ,通过式(42)计算,以上吸收的太阳辐射将使不同覆盖面温度分别提高932.1 、549.4 、962.6 、311.1 、549.2 和516.6 ℃。
通过以上分析得出,如果忽略覆盖层吸收太阳辐射,覆盖层吸收太阳辐射累积值将使覆盖层温度产生较大误差。因影响覆盖层温度的因素还包括与室内外空气的对流换热,与作物、土壤、天空温度的长波辐射等,根据以上能量交换的经验公式,覆盖层温度升高,覆盖层通过对流换热、长波辐射等形式向室内空气、土壤等传递的热量增加,进而使得覆盖层温度模型计算值与实测值保持一致。
4 结 论
本研究以玻璃温室覆盖层为研究对象,提出了温室覆盖层太阳辐射动态吸收率计算方法,进而建立一种考虑动态吸收率的温室覆盖层温度预测模型,并在山东省泰安市夏张镇开展模型精度验证试验,并将模型验证结果与相关模型对比,得出以下结论:
1)温室不同覆盖面温度预测值与测量值变化趋势较为一致,模型计算值与覆盖层温度测量值的决定系数2最小0.92,均方根误差RMSE最大为2.05 ℃,通过与相关模型对比得出本研究提出的模型具有更高的覆盖层温度预测精度。
2)本研究提出了温室覆盖层太阳辐射动态吸收率计算方法,根据该方法将覆盖层太阳辐射吸收率分为直射辐射吸收率、散射辐射吸收率与地表反射辐射吸收率分别计算,并通过该方法精确计算覆盖层吸收太阳辐射。
此外,本研究在充分验证模型正确性及精度的前提下,利用温室覆盖层太阳辐射动态吸收率计算方法对覆盖层不同试验阶段单位面积吸收太阳辐射规律进行量化分析。通过分析发现仅有南墙夏季单位面积吸收太阳辐射最少,其余覆盖层夏季单位面积吸收太阳辐射最多。夏季南屋顶和北屋顶单位面积吸收太阳辐射相近,其余季节南屋顶单位面积吸收太阳辐射大于北屋顶。北墙在任何时段单位面积吸收太阳辐射都最低。东墙和西墙单位面积吸收太阳辐射数值相近。以上研究内容及结果可为玻璃温室结构优化、作物种植、温室节能提供理论参考及相关数据,并对研究及认识太阳辐射在温室的能量分配规律具有一定指导意义。
[1] Van Beveren P J M, Bontsema J, Van Straten G, et al. Minimal heating and cooling in a modern rose greenhouse[J]. Applied Energy, 2015, 137: 97-109.
[2] Ghasemi M H, Ajabshirchi Y, Ranjbar S F, et al. Solar energy conservation in greenhouse: Thermal analysis and experimental validation[J]. Renewable Energy, 2016, 96: 509-519.
[3] Ahamed M S, Guo H, Tanino K. Development of a thermal model for simulation of supplemental heating requirements in Chinese-style solar greenhouses[J]. Computers and Electronics in Agriculture, 2018, 150: 235-244.
[4] Taki M, Rohani A, Rahmati-Joneidabad M. Solar thermal simulation and applications in greenhouse[J]. Information Processing in Agriculture, 2018, 5(1): 83-113.
[5] Panwar N L, Kaushik S C, Kothari S. Solar greenhouse an option for renewable and sustainable farming[J]. Renewable and Sustainable Energy Reviews, 2011, 15(8): 3934-3945.
[6] Abdel-Ghany A M, Ishigami Y, Goto E, et al. A method for measuring greenhouse cover temperature using a thermocouple[J]. Biosystems Engineering, 2006, 95(1): 99-109.
[7] Kimball B A. Simulation of the energy balance of a greenhouse[J]. Agricultural Meteorology, 1973, 11: 243-260.
[8] Lamrani M, Boulard T, Roy J C, et al. Air flow and temperature patterns induced in a confined greenhouse[J]. Journal of Agricultural Engineering Research, 2001, 78(1): 75-88.
[9] Molina-Aiz F D, Valera D L, Álvarez A J. Measurement and simulation of climate inside Almerı́a-type greenhouses using computational fluid dynamics[J]. Agricultural and Forest Meteorology, 2004, 125(1/2): 33-51.
[10] Abdel-Ghany A M, Kozai T. Dynamic modeling of the environment in a naturally ventilated, fog-cooled greenhouse[J]. Renewable Energy, 2006, 31(10): 1521-1539.
[11] Reyes-Rosas A, Molina-Aiz F D, Valera D L, et al. Development of a single energy balance model for prediction of temperatures inside a naturally ventilated greenhouse with polypropylene soil mulch[J]. Computers and Electronics in Agriculture, 2017, 142: 9-28.
[12] Mobtaker H G, Ajabshirchi Y, Ranjbar S F, et al. Simulation of thermal performance of solar greenhouse in north-west of Iran: An experimental validation[J]. Renewable Energy, 2019, 135: 88-97.
[13] Singh M C, Singh J P, Singh K G. Development of a microclimate model for prediction of temperatures inside a naturally ventilated greenhouse under cucumber crop in soilless media[J]. Computers and Electronics in Agriculture, 2018, 154: 227-238.
[14] 孟力力,杨其长,Gerard P A B,等. 日光温室热环境模拟模型的构建[J]. 农业工程学报,2009,25(1):164-170.
Meng Lili, Yang Qichang, Gerard P A B, et al. Visual simulation model for thermal environment in Chinese solar greenhouse[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(1): 164-170. (in Chinese with English abstract)
[15] 许红军,曹晏飞,李彦荣,等. 日光温室太阳辐射模型构建及应用[J]. 农业工程学报,2019,35(7):160-169.
Xu Hongjun, Cao Yanfei, Li Yanrong, et al. Establishment and application of solar radiation model in solar greenhouse[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(7): 160-169. (in Chinese with English abstract)
[16] 李元哲,吴德让,于竹. 日光温室微气候的模拟与实验研究[J]. 农业工程学报,1994,10(1):130-136.
Li Yuanzhe, Wu Derang, Yu Zhu. Simulation and test research of micrometeorology environment in a sun-light greenhouse[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 1994, 10(1): 130-136. (in Chinese with English abstract)
[17] 陈俐均,杜尚丰,李嘉鹏,等. 温室环境温度预测自适应机理模型参数在线识别方法[J]. 农业工程学报,2017,33(增刊1):315—321.
Chen Lijun, Du Shangfeng, Li Jiapeng, et al. Online identification method of parameters for greenhouse temperature prediction self-adapting mechanism model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(Supp.1): 315-321. (in Chinese with English abstract)
[18] 吴春艳,赵新平,郭文利. 日光温室作物热环境模拟及分析[J]. 农业工程学报,2007,23(4):190-195.
Wu Chunyan, Zhao Xinping, Guo Wenli. Simulation and analysis of the temperature inside the sunlight greenhouse[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2007, 23(4): 190-195. (in Chinese with English abstract)
[19] Duffie J A, Beckman W A. Solar Engineering of Thermal Processes: Fourth Edition[M]. The United States of America: WILEY, 2013.
[20] Kıyan M, Bingöl E, Melikoğlu M, et al. Modelling and simulation of a hybrid solar heating system for greenhouse applications using Matlab/Simulink[J]. Energy Conversion and Management, 2013, 72: 147-155.
[21] van Ooteghem Rachel J C. Optimal control design for a solar greenhouse[J]. IFAC Proceedings Volumes, 2010, 43(26): 304-309.
[22] van Ooteghem Rachel J C. Optimal Control Design for A Solar Greenhouse[D]. Wageningen: Wageningen University, 2007.
[23] Zhou Naijun, Yu Yaxiong, Yi Jinping, et al. A study on thermal calculation method for a plastic greenhouse with solar energy storage and heating[J]. Solar Energy, 2017, 142: 39-48.
[24] Al-Helal I M, Waheeb S A, Ibrahim A A, et al. Modified thermal model to predict the natural ventilation of greenhouses[J]. Energy and Buildings, 2015, 99: 1-8.
[25] Singh R D, Tiwari G N. Energy conservation in the greenhouse system: A steady state analysis[J]. Energy, 2010, 35(6): 2367-2373.
[26] Mohammadi B, Ranjbar S F, Ajabshirchi Y. Application of dynamic model to predict some inside environment variables in a semi-solar greenhouse[J]. Information Processing in Agriculture, 2018, 5(2): 279-288.
[27] Taki M, Ajabshirchi Y, Ranjbar S F, et al. Modeling and experimental validation of heat transfer and energy consumption in an innovative greenhouse structure[J]. Information Processing in Agriculture, 2016, 3(3): 157-174.
[28] 朱芳,朱松明,叶章颖,等. 密闭遮光型甲鱼温室热环境模拟与试验[J]. 农业工程学报,2014,30(10):182-192.
Zhu Fang, Zhu Songming, Ye Zhangying, et al. Thermal simulation and test in closed-shading turtle greenhouse[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(10): 182-192. (in Chinese with English abstract)
[29] 郭腾腾,涂洁磊,盛钰清,等. 基于CFD稳态模拟的光伏玻璃温室温度分布模拟计算[J]. 云南师范大学学报:自然科学版,2018,38(2):11-15.
Guo Tengteng, Tu jielei, Sheng Yuzhang, et al. Simulation calculation of photovoltaic glass greenhouse temperature distribution based on CFD steady state simulation[J]. Journal of Yunnan Normal University: Natural Sciences Edition, 2018, 38(2): 11-15. (in Chinese with English abstract)
[30] Baptista F J, Bailey B J, Meneses J F, et al. Greenhouses climate modelling. Tests, adaptation and validation of a dynamic climate model[J]. Spanish Journal of Agricultural Research, 2010, 8(2): 285-298.
[31] Singh G, Singh P P, Lubana P P S, et al. Formulation and validation of a mathematical model of the microclimate of a greenhouse[J]. Renewable Energy, 2006, 31(10): 1541-1560.
Model for predicting the temperature of glass greenhouse cover considering dynamic absorptivity
Zhang Guanshan, Li Tianhua, Hou Jialin※
(1.271018,; 2.271018,)
The cover temperature has an important effect on the thermal behavior of the greenhouse. This research developed and validated a prediction model of the cover temperature considering dynamic cover absorptivity. The absorptivity of the cover changes with the time of day and depending on many parameters such as the refractive coefficient, extinction coefficient, and thickness of the cover. The dynamic absorptivity of the cover was used to improve the model's accuracy. The absorptivity of the cover was divided into the absorptivity of beam radiation, diffuse radiation, and ground-reflected radiation. This mathematical model also considered the thermodynamic exchanges between the cover and other components of the greenhouse including the convection, shortwave and longwave radiation. A computer program adopting the MATLAB standard solver ode45 was written to find a solution to the energy equations employing a fourth-order Runge–Kutta method. The input parameters of the model were the measurement of the meteorological environment and thermo-physical characteristics of the greenhouse components including those of the soil and inside air. The thermophysical characteristics of the greenhouse were determined by the material properties of the glass greenhouse and the construction scheme, which were not affected by the geographic location of the glass greenhouse. Initial input values for these equations were the measured temperatures of cover, soil, and air at t=0. Employing the computer program model built-in MATLAB, trends of temperature in the greenhouse were acquired by solving the unsteady-state energy balance equation for the structural components of the greenhouse and estimating heat absorbed by various surfaces. The model was validated utilizing measured data of three non-continuous periods of 10 days in three seasons in the north of China in Shandong province (36°08'N, 116°95'E). To predict the model accuracy, varying statistical indicators, including the root-mean-square error (RMSE), and the square of the correlation coefficient (2) was determined from data series. The model’s accuracy was verified by comparing the calculated temperatures with experimental measurements for the glass greenhouse. The best results were obtained with RMSE=1.26 ℃ and2=0.98 for the cover temperature. The worst results were obtained with RMSE=2.05 ℃ and2=0.92 for the cover temperature. Statistical analysis confirmed that the developed model was effective in forecasting the microclimate of the greenhouse. Finally, we compared the accuracy of this model with related research abroad. With the comparison, we concluded that the accuracy of the model was higher than that of the related research abroad. Because this research considered the dynamic absorptivity of the greenhouse cover creatively. Besides, this study had an energy analysis of solar radiation flux absorbed by the cover with the experimental greenhouse as a study case. The results indicated that the south wall absorbed less solar radiation in the summer period, while other walls and roofs absorbed more solar radiation in the summer period. The solar radiation absorbed by the east wall and the west wall was almost equal. The north wall absorbed the least solar radiation compared with other walls and roofs. It is clear that the quantification of solar radiation as demonstrated here is of great interest to the growers and is essential for the model’s accuracy and greenhouse management.
temperature; models; greenhouse; cover; dynamic absorptivity; solar radiation; energy transfer
2019-12-02
2020-02-14
十三五国家重点研发计划项目智能农机装备专项“温室智能化精细生产技术与装备研发”(2017YFD0701500);山东省现代农业产业技术体系蔬菜产业创新团队项目(SDAIT-05-11)
张观山,实验师,博士生,主要从事设施农业研究。Email:zgsh9919@sdau.edu.cn
侯加林,教授,博士,主要从事设施农业研究。Email:jlhou@sdau.edu.cn
10.11975/j.issn.1002-6819.2020.05.023
S625
A
1002-6819(2020)-05-0201-11
张观山,李天华,侯加林. 考虑动态吸收率的玻璃温室覆盖层温度预测模型[J]. 农业工程学报,2020,36(5):201-211. doi:10.11975/j.issn.1002-6819.2020.05.023 http://www.tcsae.org
Zhang Guanshan, Li Tianhua, Hou Jialin. Model for predicting the temperature of glass greenhouse cover considering dynamic absorptivity[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(5): 201-211. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2020.05.023 http://www.tcsae.org

