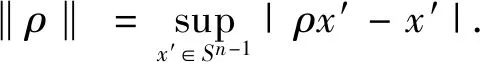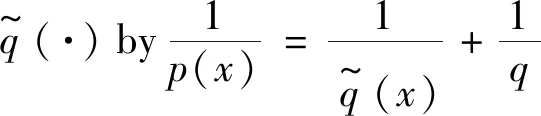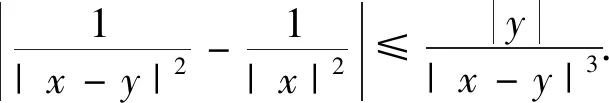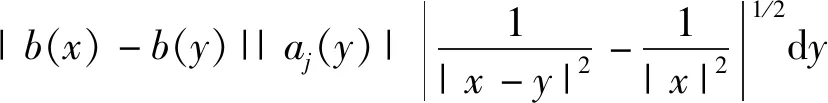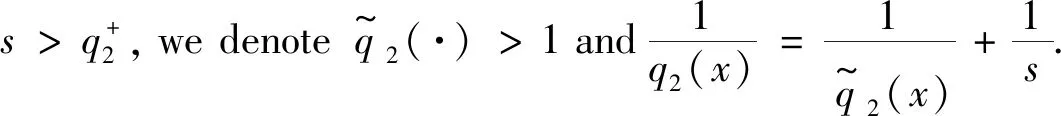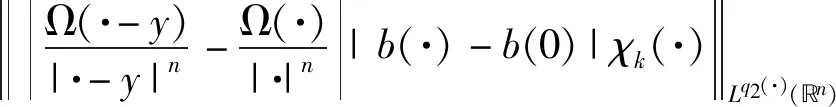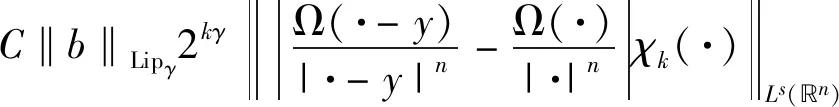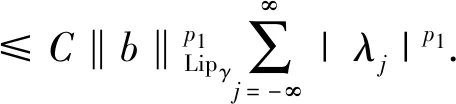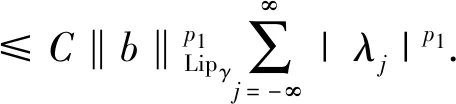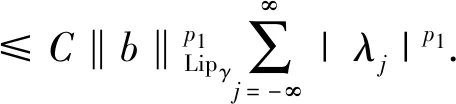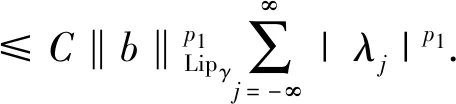The continuity for commutators of Marcinkiewicz integrals on Herz-type space with variable exponent*
WANG Hongbin
(School of Mathematics and Statistics,Shandong University of Technology,Zibo 255049,Shandong,China;School of Mathematical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China)(Received 16 August 2018;Revised 26 December 2018)
Abstract In this paper,we study the continuity of the commutators [b,μΩ] generated by Marcinkiewicz integral operators with rough kernels μΩ and Lipschitz functions b on the Herz-type space with variable exponent,where Ω∈Ls(Sn-1) for s≥1.
Keywords Herz-type space;variable exponent;Marcinkiewicz integral;rough kernel;continuity
Function spaces with variable exponent are being concerned with strong interest not only in harmonic analysis but also in applied mathematics.In the past 27 years,the theory of function spaces with variable exponent has made great progress since some elementary properties were given by Kovik and Rkosník[1]in 1991.In Refs.[2-6],the authors proved the boundedness of some integral operators on variableLpspaces,respectively.Lebesgue and Sobolev spaces with integrability exponent have been widely studied (see Refs.[3,5] and the references therein).Many applications of these spaces were given,for example,in the modeling of electrorheological fluids,in the study of image processing,and in differential equations with nonstandard growth.
On the other hand,a class of function spaces called Herz-type spaces onnhas attracted considerable attention in recent years because the interesting norm includes explicitly both local and global informations of the function.In 2011,Izuki[7]obtained Herz spaces with variable exponent.In 2012,Wang and Liu[8]introduced a certain Herz-type Hardy spaces with variable exponent.Subsequently,Wang[9-12]proved the continuity of some operators on Herz-type Hardy spaces with variable exponent.
Suppose thatSn-1denotes the unit sphere inn(n≥2) equipped with normalized Lebesgue measure.Let Ω∈Lipβ(Sn-1) for 0<β≤1 be homogeneous function of degree zero and
wherex′=x/|x| for anyx≠0.In 1958,Stein[13]introduced the Marcinkiewicz integral related to the Littlewood-Paleygfunction onnas
where
It is shown thatμΩis of weak type (1,1) and of type (p,p) for 1 For 0<γ≤1,the Lipschitz space,Lipγ(n),is defined as Lipγ(n)= Letb∈Lipγ(n).The commutator generated by the Marcinkiewicz integralμΩandbis defined by Motivated by Refs.[14-15],we will investigate the continuity of the commutators [b,μΩ] generated by Marcinkiewicz integral operators with rough kernelsμΩand Lipschitz functionsbon the Herz-type spaces with variable exponent,where Ω∈Ls(Sn-1) fors≥1. Throughout this paper,we denote the Lebesgue measure and the characteristic function of a measurable setA⊂nby |A| andχA,respectively.S(n) denotes the space of Schwartz functions,andS′(n) denotes the dual space ofS(n).The notationf≈gmeans that there exist constantsC1,C2>0 such thatC1g≤f≤C2g.LetBk={x∈n:|x|≤2k} andAk=BkBk-1fork∈.+anddenote the sets of all positive and non-negative integers,respectively.χk=χAkfork∈,ifk∈+,andIn addition,δ2denotes the same as in Lemma 1.3. Firstly we give some notations and basic definitions on variable Lebesgue spaces. Given an open setE⊂nand a measurable functionp(·):E→[1,∞).p′(·) is the conjugate exponent defined byp′(·)=p(·)/(p(·)-1). The setP(E) consists of allp(·):E→[1,∞) satisfying p-=essinf{p(x):x∈E}>1, p+=esssup{p(x):x∈E}<∞. ByLp(·)(E) we denote the space of all measurable functionsfonEsuch that for someλ>0, This is a Banach function space with respect to the Luxemburg-Nakano norm The setB(n) consists ofp(·)∈P(n) satisfying the condition that the Hardy-Littlewood maximal operatorMis bounded onLp(·)(n). In variableLpspaces there are some important lemmas[1,3,7],which are given as follows. Lemma1.1Ifp(·)∈P(n) and satisfies |x-y|≤1/2, (1) and (2) thenp(·)∈B(n),that is,the Hardy-Littlewood maximal operatorMbeing bounded onLp(·)(n). Lemma1.2Supposeq(·)∈B(n).Then there exists a constantC>0 such that for all ballsBinn, Lemma1.3Letq(·)∈B(n).Then there exists a positive constantCsuch that for all ballsBinnand all measurable subsetsS⊂B, and whereδ1andδ2are constants with 0<δ1,δ2<1. Lemma1.4(GeneralizedHölderinequality) Letp(·)∈Ρ(n).Iff∈Lp(·)(n)andg∈Lp′(·)(n),thenfgis integrable onnand whererp=1+1/p--1/p+. Next we recall some definitions and one lemma for the Herz-type spaces with variable exponent given in Refs.[7-8]. Definition1.1Letα∈,0 LetGN(f)(x) be the grand maximal function off(x) defined by whereAN={φ∈S( Definition1.2Letα∈,0 Forx∈we denote by [x] the largest integer less than or equal tox. Definition1.3Letnδ2≤α<∞,q(·)∈P(n),n),and integers≥[α-nδ2]. (i) A functiona(x) onnis said to be a central (α,q(·))-atom,if it satisfies 1) suppa⊂B(0,r)={x∈n:|x| 2) ‖a‖Lq(·)(n)≤|B(0,r)|-α/n, (ii) A functiona(x) onnis said to be a central (α,q(·))-atom of the restricted type,if it satisfies the above conditions 2) and 3) and 1)′ suppa⊂B(0,r),r≥1. Ifr=2kfor somek∈in Definition 1.3,then the corresponding central (α,q(·))-atom is called a dyadic central (α,q(·))-atom. Lemma1.5Letnδ2≤α<∞,0 in the sense ofS′(n),where eachakis a central (α,q(·))-atom(or central (α,q(·))-atom of restricted type) with support contained inBkandMoreover, where the infimum is taken over all above decompositions off. Letb∈Lipγ(n).It is easy to know thatwhere Theorem2.1Suppose thatb∈Lipγ(n) with 0<γ≤1.Ifq1(·)∈P(n) satisfies conditions (1) and (2) in Lemma 1.1 with1/q1(x)-1/q2(x)=γ/n,Then [b,μΩ] is bounded fromLq1(·)(n) toLq2(·)(n). Next,we will give the continuity about the commutator[b,μΩ] on Herz-type Hardy spaces with variable exponent.Before stating our result,let us recall the definition of theLs-Dini condition.We say that Ω satisfies theLs-Dini condition if Ω(x′)∈Ls(Sn-1) withs≥1 is homogeneous of degree zero onn,and whereωs(δ) denotes the integral modulus of continuity of ordersof Ω defined by Theorem2.2Suppose thatb∈Lipγ(n) with 0<γ≤1.Ifq1(·)∈P(n) satisfies conditions (1) and (2) in Lemma 1.1 with1/q1(x)-1/q2(x)=γ/n,and satisfies In the proof of Theorem 2.2,we need the following lemmas in Refs.[3,5,17-18]. Lemma2.1GivenEandp(·)∈P(E),letf:E×E→be a measurable function (with respect to product measure) such that for almost everyy∈E,f(·,y)∈Lp(·)(E).Then for all measurable functionsfandg. Lemma2.3Letp(·)∈P(n) satisfies conditions (1) and (2) in Lemma 1.1.Then for every cube (or ball)Q⊂n,where Lemma2.4Suppose that Ω satisfies theLs-Dini condition (1≤s<∞).Then for anyR>0 andx∈n,when |y| =∶U1+U2. (3) We first estimateU1.Note that |[b,μΩ](aj)(x)|≤ =∶U11+U12. Whenx∈Akand |x-y|≤twitht≤|x|,it follows fromj≤k-2 that |x-y|~|x|.By mean value theorem we have (4) Then by (4),the Minkowski inequality,the generalized Hölder inequality and the vanishing moments ofajwe have |b(x)-b(y)||aj(y)|dy. Similarly,we considerU12.Noting that |x-y|~|x|,by the Minkowski inequality and the vanishing moments ofajwe have |b(x)-b(y)||aj(y)|dy. So we have |b(x)-b(y)||aj(y)|dy. Using Lemma 2.1 and the Minkowski inequality we have ‖[b,μΩ](aj)χk‖Lq2(·)(n) |b(0)-b(y)||aj(y)|dy =∶U13+U14. When |Bk|≤2nandxk∈Bk,by Lemma 2.3 we have When |Bk|≥1 we have So we obtain Meanwhile,by Lemma 2.4 we have So by the generalized Hölder inequality we have |b(·)-b(0)|χk(·)‖Lq2(·)(n)|aj(y)|dy ≤C‖b‖Lipγ2-kn+(j-k)γ‖χBk‖Lq1(·)(n) ‖aj‖Lq1(·)(n)‖χBj‖Lq′1(·)(n). (5) ForU14,similar to the method ofU13we have ≤C2-kn+(j-k)γ-kγ‖χBk‖Lq1(·)(n). So by the generalized Hölder inequality we have |b(0)-b(y)||aj(y)|dy ≤C2-kn+(j-k)γ-kγ‖χBk‖Lq1(·)(n) ≤C‖b‖Lipγ2-kn+2(j-k)γ‖χBk‖Lq1(·)(n) ≤C‖b‖Lipγ2-kn+(j-k)γ‖χBk‖Lq1(·)(n) ‖χBj‖Lq′1(·)(n)‖aj‖Lq1(·)(n). (6) By (5),(6),Lemma 1.2 and Lemma 1.3 we have ‖[b,μΩ](aj)χk‖Lq2(·)(n) ≤C‖b‖Lipγ2-kn+(j-k)γ‖χBk‖Lq1(·)(n) ‖aj‖Lq1(·)(n)‖χBj‖Lq′1(·)(n) ≤C2-jα+(j-k)(γ+nδ2)‖b‖Lipγ. So we have When 1 (7) When 0 (8) Next we estimateU2,by the (Lq1(·)(n),Lq2(·)(n))-boundedness of the commutator [b,μΩ] we have If 0 (9) If 1 (10) Thus,by (3),(7)-(10) we complete the proof of Theorem 2.2.1 Preliminaries
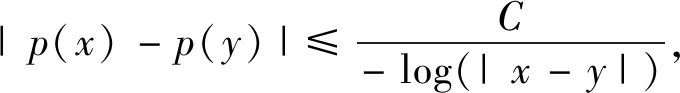

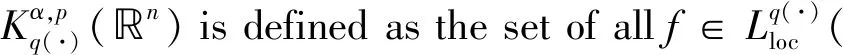
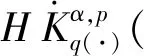
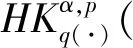
2 Main results and their proofs