多算法组合的河流水质预测方法研究

肖荣平，葛卉犇，孙 新

(江苏淮阴水利建设有限公司，江苏 淮安 223000)

水是生命之源，地表水是水资源的主要存在形式，目前全球的水资源短缺已经变得越来越严重，而水质下降更是一个严重的问题。科技的发展和人类社会的进步对水环境的质量造成了很大影响，有些水体的自净能力已经无法处理人类所排放的污染物量。根据相关统计，我国水环境污染发生的频率在所有环境污染中发生的次数最多，而河流水污染问题又是水环境污染的首要问题。过去我国曾发生了很多次较为典型的水体污染事件，这些水污染事件给当地居民的生产、生活造成了重大影响。对于一条河流而言，其自净能力在一定时间内可以维持恒定，所以当外界排放的污染物含量增大时，将会导致水体污染严重，此时，就需要人为采取有效的水体处理方法。水质评价是一项重要工作，此外，根据当下的水质数据资料预测未来一段时间内的水质变化也是一项必要的工作，通过进行水质预测，可以尽早研究一些防治水体污染、改善水质的措施和方法，避免水质进一步恶化。在水质预测的过程中，普遍采用的方法主要有3类，分别为时间序列法、结构分析法、系统分析法。总结这3类方法可以发现，这几种方法的基本思路都是以一些表面的参数序列为基础，对水质的未来变化情况进行预测，而一些深入的分析较为缺乏。以时间序列为基础是使用最为广泛的一种，但是由于时间序列中含有一些噪声序列，而噪声序列对预测结果也具有一定的影响，目前一些方法对噪声序列的考虑不够充分。在具体的方法应用上，预测方法又有基于支持向量机、基于人工神经网络、基于灰色系统理论、基于数理统计等。吴涛等基于Holt-Winters时间序列模型预测了三峡库区水质的变化情况，预测结果和实际结果较为吻合。张旭东等通过研究提出了一种基于改进的实数编码遗传算法优化BP神经网络(IGA-BP)的水质预测新模型，该模型的收敛速度快，结果可以满足要求，但是该模型没有对时间序列进行充分应用。Xiang Y等基于粒子群的LS-SVM预测了水质，通过优化LS-SVM得到的结果较好。在这些方法中，时间序列是操作的对象，但是如果可以对时间序列进行充分利用后，则预测结果和实测结果更接近。离散小波变换方法在时间信号处理方面具有显著优势，灰色系统理论在实际的时间序列满足要求时，也具有较好的预测效果，广义自回归条件异方差模型可以对噪声序列进行有效处理。当后两种方法在单独作用时，都存在一定的缺陷，而如果将灰色系统理论和广义自回归条件异方差模型结合起来，并引入小波变换对时间序列进行处理，即将3种方法结合起来，构成一个组合预测方法，可以起到取长补短的作用。基于这方面分析，以3种方法为基础，通过研究将3种方法结合起来，提出合理的组合预测方法，并给出可行的计算流程，在Matlab编程中实现组合预测方法。结合实际河流，对河流的水质情况进行预测，并和实际监测结果对比，判断组合预测方法预测的精度和可靠性。

1 组合预测方法

1.1 离散小波变换

离散小波变换在处理时间连续信号中有着广泛的应用，在时域和频域分析中是一个有效的工具。这里对所使用的离散小波变换进行分析。设ψ(t)是一个平方并可以积分的函数，基于傅里叶变换对该函数进行积分，并保证积分结果满足式(1)的要求，即

(1)

满足这样的条件后，ψ(t)可以进行式(2)的变换获得函数族，即

(2)

式中，α—伸缩尺度，用于对特定基函数的小波变换尺度的伸缩变化进行反映，α∈R，且α≠0；β—不同的平移度，用于对平移位置和大小进行反映，β∈R。

用函数族加权和的方式表示一个初始时间序列，这就是小波变换的核心，该函数族加权和的表达式如下：

(3)

采用小波变换对连续时间序列点数进行处理之后，获得的时间点数相比于未处理要少，但是可能会出现失真情况，所以需要采用合适的重构算法进行处理，这里通过式(4)来实现，即

(4)

1.2 灰色GM(1，1)预测方法

在对时间序列建立预测模型的过程中，采用灰色GM(1，1)模型可以保证预测结果的精度较高，通过分析，结合水质预测的过程，提出如下的建模基本过程。

(1)获得原始灰色序列，原始灰色序列表示为：

X(0)=[x(0)(1)，x(0)(2)，…，x(0)(n)]

(5)

式中，n—样本数量。

(2)对原始灰色序列采用累加的方法进行第一次累加，得到累加之后的时间序列，即

X(1)=[x(1)(1)，x(1)(2)，…，x(1)(n)]

(6)

Z(1)=[z(1)(1)，z(1)(2)，…，z(1)(n)]

(7)

式中，z(1)(k)=[x(1)(k)+x(1)(k-1)]/2。

(3)基于灰色微分方程，构建白微分方程，即灰色微分方程如式(8)，白微分方程如式(9)。

b=x(0)(k)+az(1)(k)

(8)

(9)

式中，a，b分别为发展系数和待定系数。

(4)通过最小二乘法计算a，b，即

[a，b]T=(BTB)-1BTY

(10)

式中，Y=[X(0)(2)，…，X(0)(n)]T；

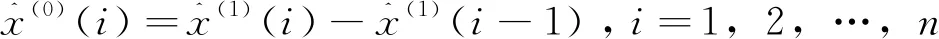
(11)

式中，t=0，1，2，…，n。

对式(11)进行累加还原操作，就可以得到式(12)，该公式就是灰色预测模型的表达式，即

(12)

计算残差，当残差最小时，对应的预测精度最高，经过分析，为了获得较高的预测精度，保证预测精度为一级，对应的模型表达式为

x(1)(t)=[x(0)(1)-7.439/0.009]e-0.009(t-1)
+7.439/0.009

(13)

1.3 广义自回归条件异方差模型

在预测小波变换导致缺失的时间序列时，采用广义自回归条件异方差模型具有显著的优势，所以采用这个模型弥补小波变换的缺陷，该模型的表达式为

yt=λyt-1+εt

(14)

(15)

式中，yt—研究的时间序列；εt—误差；—误差的平方。

基于广义自回归条件异方差方法建立模型的步骤为：检验时间序列的平稳性、识别模型、定阶模型、估计参数、显著性分析、预测模型，具体可以参照相关文献[16]。

1.43个模型的组合

灰色时间序列具有较强的模糊性，且多为非线性序列，复杂性高，仅仅采用GM(1，1)模型进行预测，所获得的结果精度尚不能满足要求，通过前文分析，这里提出将原始时间序列采用DB3正交小波分解法进行处理，从而将时间序列分为概貌时间序列和3个细节时间序列，前者含有很多原始序列包含的信息，后者是经过小波分解过滤的序列。预测概貌时间序列通过GM(1，1)模型实现，预测细节时间序列通过GARCH模型实现，将两者预测结果求和，即可得到最终预测结果。对3个预测模型进行组合，保证了预测结果的精度，具有取长补短的作用。根据基本原理，提出该组合预测方法的过程和算法要求，具体如下：

(1)选择待分解的原始时间序列，采用离散小波变换对该序列进行分解处理，获得子序列，采用重构方法处理子序列，进而获得1个平滑的概貌时间序列和3个细节时间序列，其中细节时间序列的波动性较大。

(2)采用灰色GM(1，1)模型预测概貌时间序列的预测值。

(3)采用广义自回归条件异方差模型预测3个细节时间序列的预测值。

(4)将上述两类时间序列的预测值进行求和，获得最终预测值。

通过在Matlab中编程，实现该算法的操作。

2 预测方法的应用

利用前文建立的组合预测方法对江苏淮安的某河流水质污染指标进行预测分析，根据该河流的排污情况、实际被污染情况以及上下游关系，将河流分为4段，从上游到下游分别表示为A段、B段、C段、D段。研究的污染指标有溶解氧DO、高锰酸盐指数CODMn、氨氮含量NH3-N。实际中，选择了2018年连续8周的实际监测结果，并利用该组合预测方法对3个指标在同一时期内的结果进行了预测，绘制了实测值和预测值的对比曲线，如图1—4所示。

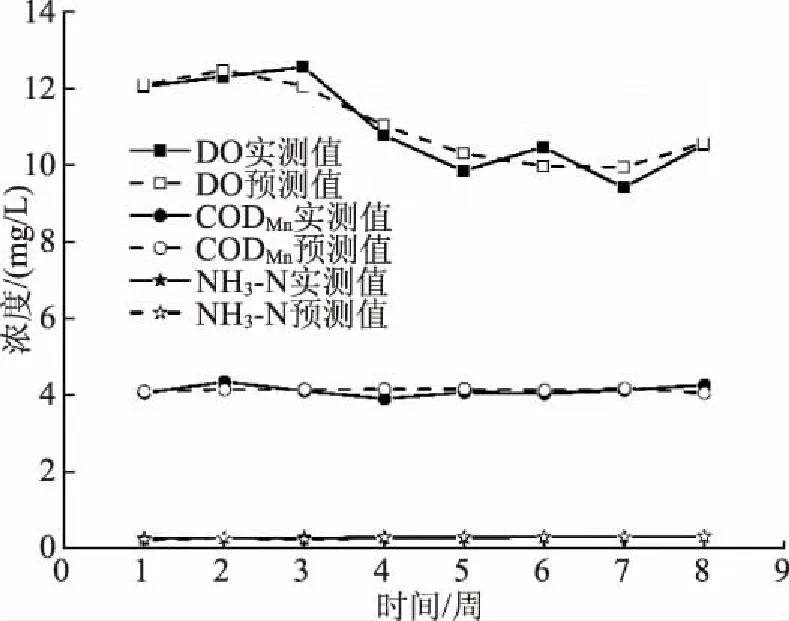
图1 A段实测值和预测值曲线

图2 B段实测值和预测值曲线

图3 C段实测值和预测值曲线

图4 D段实测值和预测值曲线

从图1—4可以看出，河流A段溶解氧含量最高，在观测时段内，高锰酸盐指数和氨氮含量保持平稳，几乎不发生变化，水质较好，该段受到的污染较小，3个指标的预测值和实测值均很接近。河流B段的溶解氧较A段有所降低，在整个观测时段内，变化幅度较小，高锰酸盐指数和氨氮含量比A段有所提高，水质有较小的下降，在第5周～第8周期间，溶解氧的预测值和实测值有较大的偏差，但是总体而言，3个指标的预测值和实测值吻合度较好。C段的溶解氧含量在后半段时间内显著增大，高锰酸盐指数也显著下降，氨氮含量并没有发生显著变化，说明该段河流的水质正在逐渐改善，3个指标的预测值和实测值吻合度较好。D段河流水质随着时间的进行，溶解氧含量呈现下降趋势，高锰酸盐指数有小幅增大，说明水质在逐渐下降，这主要是因为D段位于河流的下游，受污染较严重，氨氮含量的变化并不显著，3个指标的预测值和实测值吻合度高。分析4段的实测结果和预测结果，溶解氧、高猛酸盐指数、氨氮含量的平均相对误差范围分别为2.81%～6.02%、1.71%～5.03%、2.29%～9.53%，绝对误差也较小，因此，3个指标的预测值和实测值均有较好的吻合度，说明该组合预测方法可以有效预测短时间内的水质变化情况。

3 结论

以河流水质的准确预测为研究目的，通过研究得到以下结论。

(1)分析了离散小波变换、灰色GM(1，1)预测方法、广义自回归条件异方差模型，说明了每个方法或模型的具体思路，实现了3种方法的有机组合，提出了组合预测方法，并给出了该方法的具体实现过程和算法，利用Matlab编程实现了该算法的操作。

(2)以江苏某河流为分析对象，将该河流分为4段，分析指标为溶解氧、高锰酸盐指数、氨氮含量，利用提出的组合预测方法预测了4段河流3个参数的变化情况，表明了预测值和实测值的变化趋势一致，吻合度高，能够有效地预测短时间内水质的变化情况。