风电机组变桨轴承螺栓拧紧工艺优化研究

文 | 任延博，韩锐，赵爽

（作者单位：国电联合动力技术有限公司）

随着风电机组技术的不断发展，单机功率持续提升，轮毂的外形尺寸不断增大（以3.0MW机型为例，轴承顶端螺栓距离地面约4.5m），变桨轴承螺栓的数量亦不断增加，这对变桨轴承螺栓的拧紧工艺提出了更高的要求。

国家标准GB/T19568―2017《风力发电机组装配和安装规范》中第3.2条（装配连接要求）中对于呈环形分布的多颗螺栓的拧紧工艺只做了原则要求，没有进行详细说明。为了保证多颗螺栓拧紧后的预紧力均匀分布，螺栓的拧紧顺序如图1所示。

此方法可以最大限度地保证螺栓预紧力的均匀分布，但在实际执行中有两个困难：一是螺栓的拧紧顺序复杂，找位困难；二是轮毂与变桨轴承的高度高，操作人员需要往复地上下攀爬，才能保证螺栓按照规定顺序拧紧，不仅劳动强度大，且操作人员在上下攀爬过程中也存在安全隐患。

为此，本文提出一种优化方法，优化后的拧紧顺序如图2所示：首先拧紧8颗螺栓，使其呈“米”字形均匀分布，8颗螺栓将环形分布的多颗螺栓平均分成8等份，将每等份内的螺栓依次拧紧，8段螺栓仍然依照“十”字交叉对角拧紧法依次拧紧。

试验方法

一、试验原理

螺栓拧紧采取扭矩控制法。螺栓的拧紧力矩T与轴向预紧力F之间为线性关系，对应的关系式为：

式中，d为螺栓的直径，K为扭矩系数，F为预紧力。

螺栓拧紧时，其材料变形会经过两个阶段，分别是弹性区与塑性区。在弹性区采用扭矩法控制时，确定了起始点扭矩后，通过改变螺栓旋转角度来控制螺栓的轴向预紧力。弹性区轴向预紧力F与旋转角度θ成正比，对应的关系为：

式中，C为螺栓连接刚度系数，P为螺距。

由公式可知：螺栓的预紧力与旋转角度成正比，可以将螺栓转角的变化等同于螺栓的预紧力。故根据转角的变化（相同的拧紧力矩导致的转角变化），来判断螺栓预紧力的变化。

将公式（2）代入公式（1）中，可得：

变桨轴承螺栓拧紧采用扭矩法控制。假设螺栓材质C完全相同，扭矩系数K一致，当螺栓处于弹性变形区域时，对相同规格的螺栓施加同样的扭矩，螺栓转动的角度相同。

对两种拧紧顺序的螺栓施加相同的力矩，如果转角的均值不相等，则说明拧紧顺序对于螺栓拧紧有显著影响，优化方案不可行；如果均值相等，则说明无显著影响，优化方案可行。

二、试验设计

使用电动力矩扳手分别按照图1与图2的顺序分三次进行螺栓拧紧，三次的拧紧力矩分别是1000N·m、2000N·m与2570N·m。拧紧作业完成后记录各螺栓的转角（每种拧紧顺序需记录三组转角数据，分别是1000N·m、2000N·m与2570N·m扭矩完成后的螺栓转动角度），并对螺栓在2000N·m及2570N·m力矩作用下的转动角度分别进行双样本T检验（1000N·m的螺栓转角数据因为起始力矩不一致，故对该数据不做分析，仅供参考），确定最优的拧紧顺序。

试验用的螺栓需取自于同一批次，两个变桨轴承必须装配于同一轮毂的两个法兰面，二硫化钼采用可赛新1769，执行全涂抹工艺。

试验数据及分析

依据图1与图2的顺序分别进行螺栓拧紧，记录各螺栓的转动角度，数据如表1与表2所示（试验的数据较多，表格中仅列出了其中10颗螺栓的拧紧数据）。

假定螺栓按照工艺1拧紧方法进行拧紧，其用2000N·m与2570N·m力矩拧紧时，转角的均值及标准差分别为μ1、σ1，μ2、σ2。按照工艺2拧紧方法进行拧紧，其用2000N·m与2570N·m力矩拧紧时，转角的均值及标准差分别为为μ3、σ3，μ4、σ4。分别对拧紧力矩为 2000N ·m的工艺1与工艺2的转角及拧紧力矩为2570N·m的工艺1与工艺2的转角进行双样本T检验，判断其均值是否相等。

双样本T检验，有三个条件需满足，分别是：

（1）正态性检验：

假设样本 yi1，yi2，yi3，yi4，…均为来自于正态总体的样本。

（2）方差齐性检验：

假定两种拧紧工艺在相同拧紧力矩作用下其转角的方差相同，即。

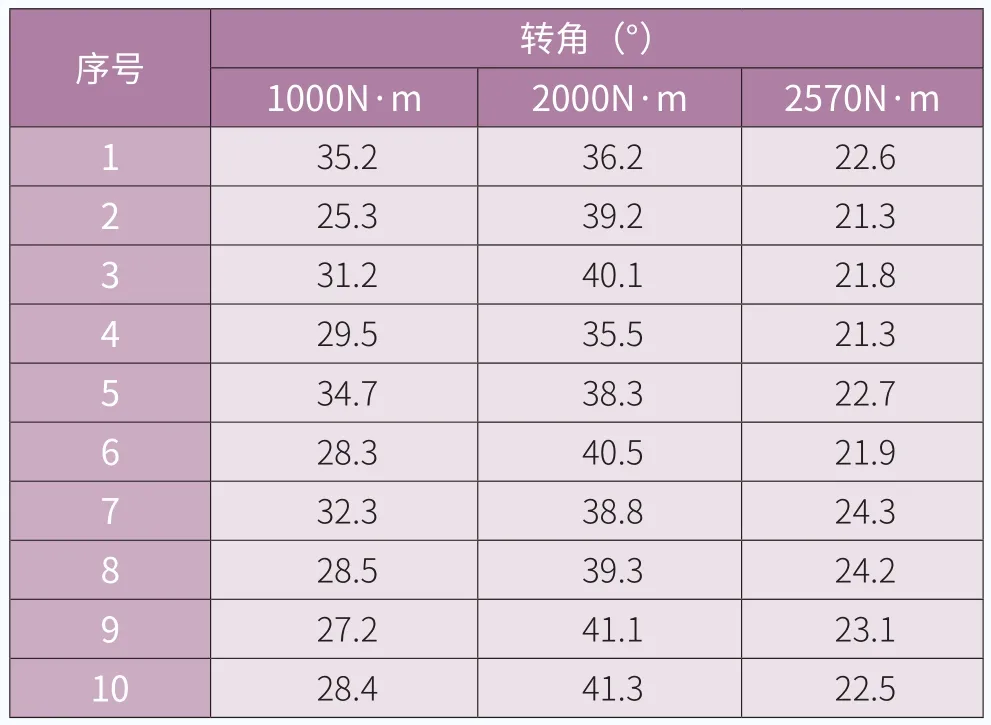
表2 拧紧工艺2的螺栓转角数据统计

（3）独立性：

工艺1与工艺2的拧紧数据无交叉，符合独立性要求。

一、正态性检验

对收集的数据进行正态性检验，检验结果如下：

（1）当扭矩为2000N·m时，79颗螺栓转动角度正态分析结果如图3与图4所示。

根据两种拧紧工艺转角数据的正态分布分析结果，其P值分别为0.629与0.509，均大于0.05，故可以判断两组数据符合正态分布。

（2）当扭矩为2570N·m时，79颗螺栓转动角度正态分析结果如图5与图6所示。

根据两种拧紧工艺转角数据的正态分布分析结果，其P值分别为0.333与0.684，均大于0.05，故可以判断两组数据均符合正态分布。

二、方差齐性检验

对两种拧紧工艺下的2000N·m及2570N·m的转角数据进行方差齐性检验：

（1）当扭矩为2000N·m时，分别采用工艺1与工艺2进行螺栓拧紧后，螺栓转角的方差齐性检验结果如表3所示。

分析结果显示，P值为0.065，大于0.05，故选择原假设。当扭矩为2000N·m时，工艺1与工艺2的方差相等。

（2）当扭矩为2570N·m时，分别采用工艺1与工艺2进行螺栓拧紧后，螺栓转角的方差齐性检验结果如表4所示。

分析结果显示，P值为0.614，大于0.05，故选择原假设。当拧紧力矩为2570N·m时，螺栓拧紧采用工艺1与工艺2的方差相等。

表3 扭矩为2000N·m的F检验结果

表4 扭矩为2570N·m的F检验结果

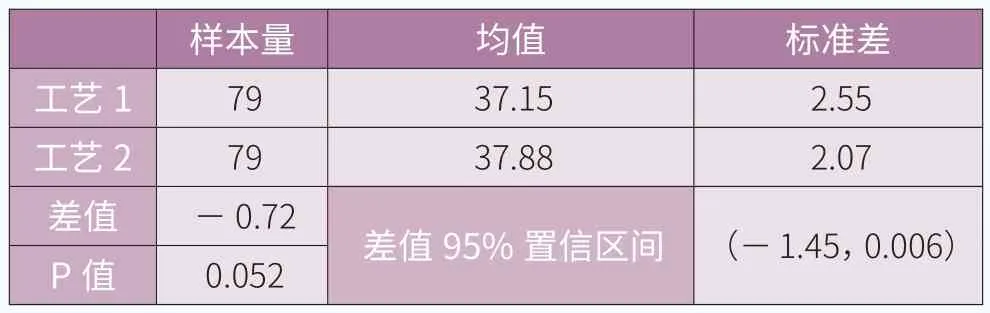
表5 扭矩为2000N·m的双T检验结果

表6 扭矩为2570N·m的双T检验结果

三、双样本T检验

工艺1与工艺2的拧紧数据符合正态分布，在2000N·m及2570N·m状态下，其标准差也相等，使用MINITAB软件对数据进行双样本T检验，来判断其均值是否相等。

原假设 ：μ1＝ μ3，μ2＝ μ4

备择假设 ：μ1≠ μ3，μ2≠ μ4

（1）当扭矩为2000N·m时，分别采用工艺1与工艺2进行螺栓拧紧后，双样本T检验结果如表5所示。

分析结果显示，P值为0.052，大于0.05，故选择原假设μ1＝μ3。即当拧紧力矩为2000N·m时，螺栓按照工艺1与工艺2的顺序拧紧后，转角均值相等。

（2）当扭矩为2570N·m时，分别采用工艺1与工艺2进行螺栓拧紧后，螺栓转角双样本T检验结果如表6所示。

分析结果显示，P值为0.413，大于0.05，故选择原假设μ2＝μ4。即当拧紧力矩为2570N·m时，螺栓按照工艺1与工艺2的顺序拧紧后，转角均值相等。

由上述试验结果可知，在置信水平为95%的情况下，高强度螺栓依据优化后的拧紧顺序进行拧紧作业，其转角均值与标准工艺下的转角均值相同。即采用两种工艺进行螺栓拧紧，最后螺栓的预紧力是相同的，满足设计要求，优化方案可行。

结语

本文研究表明，优化方案可以用于螺栓拧紧。除了风电机组变桨轴承螺栓，偏航轴承螺栓以及类似工位的环形分布多颗螺栓都可以依据优化工艺原理进行工艺变更，优化拧紧顺序。

优化方案在保证螺栓拧紧质量的前提下可以有效提高装配效率，降低操作者的劳动强度，同时可以减小操作者进行拧紧作业时的安全风险。