基于SIFT的高分二号全色与多光谱影像配准算法
王森

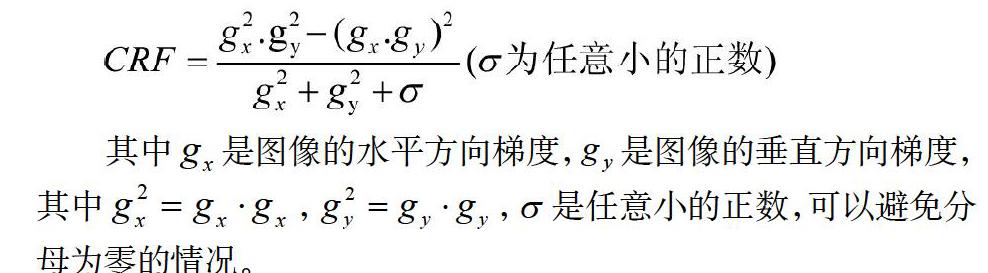
摘要:传统的SIFT算法在配准高分二号全色与多光谱影像时配准效率较低,本文使用一种新的配准策略:首先对图像进行区域划分并计算每个区域的信息熵,只针对信息熵较大的部分采用改进的Harris算法提取特征点,然后使用SIFT算法描述特征点并进行粗匹配,再用PROSAC进行特征点的提纯,实现精匹配,最后完成图像配准。
关键词:高分二号;图像配准;信息熵;SIFT;PROSAC
中图分类号:TP391.4 文献标识码:A 文章编号:1007-9416(2020)01-0104-02
0 引言
在遥感图像处理中,图像配准是很重要的处理环节。配准精度的高低直接会影响到后续的图像处理质量,因此对遥感图像配准进行深入的研究具有很重要的现实意义。近年来Harris算子和SIFT算子在图像配准领域应用较为广泛,这两种方法在处理普通图像时能够取得较好的配准效果,但是对于遥感图像配准而言往往配准精度较低。因此本文基于这两种算法对高分二号卫星图像的配准方法进行研究,从而充分利用这两种算法的优点。
Harris[1]角点检测算法是通过微分算子计算像素点在任意方向上的灰度变化,并根据角点响应函数的值来判断目标像素点是否为角点。该算法运算量较小,且提取的角点分布较为均匀。尺度不变特征变换(SIFT)[2]算法是图像配准领域较为经典的一种算法,SIFT特征对图像的尺度、旋转、平移等具有不变性,该算法的主要步骤包括:尺度空间构造、极值点检测、特征点主方向分配、特征描述子生成。SIFT算法在普通图像中的配准效果较好,但是对于大幅面的遥感图像往往具有配准速度慢、精度低等特点。配准速度慢主要体现在检测到的特征点数量多,从而在特征描述阶段会有较多的时间消耗,因此本文在特征检测部分使用改进的Harris算法代替SIFT算法进行特征检测。
1 基于Harris-SIFT的图像配准算法
1.1 特征点检测
经典的Harris算子检测出的角点不具有尺度不变性,因此本文使用Harris-Laplace[3]算法进行角点检测,使其具有尺度不变性。Harris算子是通过角点响应函数CRF(corner response function)的值来判断该点是否为角点,当CRF的值超过所设定的阈值时,则认为该点为需要的角点。但是CRF值的计算会受到经验常数k的影响,进而会影响到后续的配准效果,因此为了避免k值的选取,本文使用改进的角点响应函数[4],计算式为:
其中是图像的水平方向梯度,是图像的垂直方向梯度,其中,,是任意小的正数,可以避免分母为零的情况。
针对该改进的Harris算法依然存在无效的角点的问题,本文参考王崴等[5]提出的在当前的目标像素点8邻域的范围内统计与之相似的像素点个数,以此来剔除无效的角点。由于高分二号图像的特殊性,且波段间灰度存在较大的差异,这样容易使角点的定位存在偏差。故需要对用上述方法检测到的角点进行精定位,本文参考经典的Forstner[6]算子对角点进行精定位。
1.2 特征描述子生成
由于本文不直接对整幅图像进行特征检测,而仅对信息熵较大的区域使用改进的Harris算子检测角点特征,这样大大的降低了算法的运算量,所以不必再为了进一步提高运算速度而降低特征描述符的维数,因为在降维的同时可能会使配准精度降低。因此,为了确保配准精度,本文使用传统的SIFT算法进行特征描述,生成128维特征向量,具体可参考文献[2]中的方法。
1.3 针对高分二号卫星影像的配准方法
由于高分二号图像的数据量较大,因此传统的配准策略在此已不能满足实时性的要求。本文方法为:首先对整幅图像进行区域划分[7]并计算各区域信息熵,然后针对信息熵较大的区域使用改进的Harris算法进行特征提取,从而缩短特征检测的时间,而且能够使特征点在整幅图像中分布均匀。之后使用SIFT算法对特征点进行描述并且进行粗匹配,然后使用PROSAC[8]算法进一步提纯特征点并估算出变换模型参数,从而实现最终的图像配准。
2 实验分析
本文选取全色影像为基准图像,由于多光谱影像中的近红外波段和全色影像存在较大的灰度差异,故以近红外波段为例作为待配准图像进行实验更能验证配准算法的有效性,全色影像大小为2286×2225,近红外波段影像大小为746×749。本文使用VS2013结合GDAL库编程。使用传统的SIFT算法作为对比实验,本文算法实验结果如图1所示,两种算法配准效果比较如表1所示。实验结果表明,本文算法明显比SIFT算法检测到的特征点少、配准速度快,在提高配准速度的同时,配准精度也较SIFT算法高。
3 结语
本文针对高分二号遥感图像提出了一种在区域划分的基础上,使用改进的Harris算子和SIFT算子相结合的图像配准方法。实验证明,该算法提取的特征点较SIFT算法更少且更均匀,配准速度和配准精度都较SIFT算法有显著的提高。
参考文献
[1] Harris C,Stephens M.A combined corner and edge detector[C].Proceedings of the Alvey Vision Conference,Manchester,UK,1988:147-151.
[2] Lowe D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
[3] Mikolajczyk K,Schmid C.Scale & affine invariant interest point detectors[J].International Journal of Computer Vision,2004,60(1):63-86.
[4] 毛晨,錢惟贤,顾国华,等.基于双边滤波的Harris角点检测[J].红外技术,2014,36(10):812-815+819.
[5] 王崴,唐一平,任娟莉,等.一种改进的Harris角点提取算法[J].光学精密工程,2008(10):1995-2001.
[6] 张艳,张志成.混合Forstner算法和SIFT灰度图像特征点提取[J].科技通报,2012(10):64-70.
[7] 李玉峰,王竹筠.基于Harris-SIFT特征匹配的图像自动配准算法研究[J].电视技术,2015,39(23):26-30.
[8] CHUM O,MATAS J.Matching with PROSAC-progressive sample consensus[C].IEEE Computer Society Conference on Computer Vision & Pattern Recognition(ICCV),Beijing:IEEE,2005:220-226.

