基于BDSBAS的机载端完好性算法研究
于耕 李浩


摘要:用户差分距离误差、区域用户距离误差是判断差分精度能否符合系统完好性性能标准的主要参数,本文基于北斗星级增强系统在校验电离层延迟时,使用格网电离层校正模型的二次曲面拟合算法得到电离层延迟,计算用户差分距离误差、区域用户距离误差。结果表明,二次曲面拟合算法能满足机载端在飞行各阶段中对北斗卫星导航系统精度与完好性的要求。
关键词:北斗导航星基增强系统;二次曲面拟合;用户差分距离误差;区域用户距离精度
中图分类号:TP391 文献标识码:A 文章编号:1007-9416(2020)01-0098-02
0 引言
用户差分距离误差(UDRE)与区域用户距离误差(RURA)都可以判断监测的北斗卫星的差分精度是否可以符合完好性性能的要求。两者的计算方法大致相同,而其中的差异就是计算校正后的伪距Rm时,UDRE值使用的是格网电离层模型对电离层延迟校正,而RURA使用的通过单频校正法对电离层延迟校正。
1 基本原理
以UDRE计算方法为例,如下是UDRE值的计算方法:
Pr(UDRE>卫星星历及钟差改正误差)≥99.9% (1)
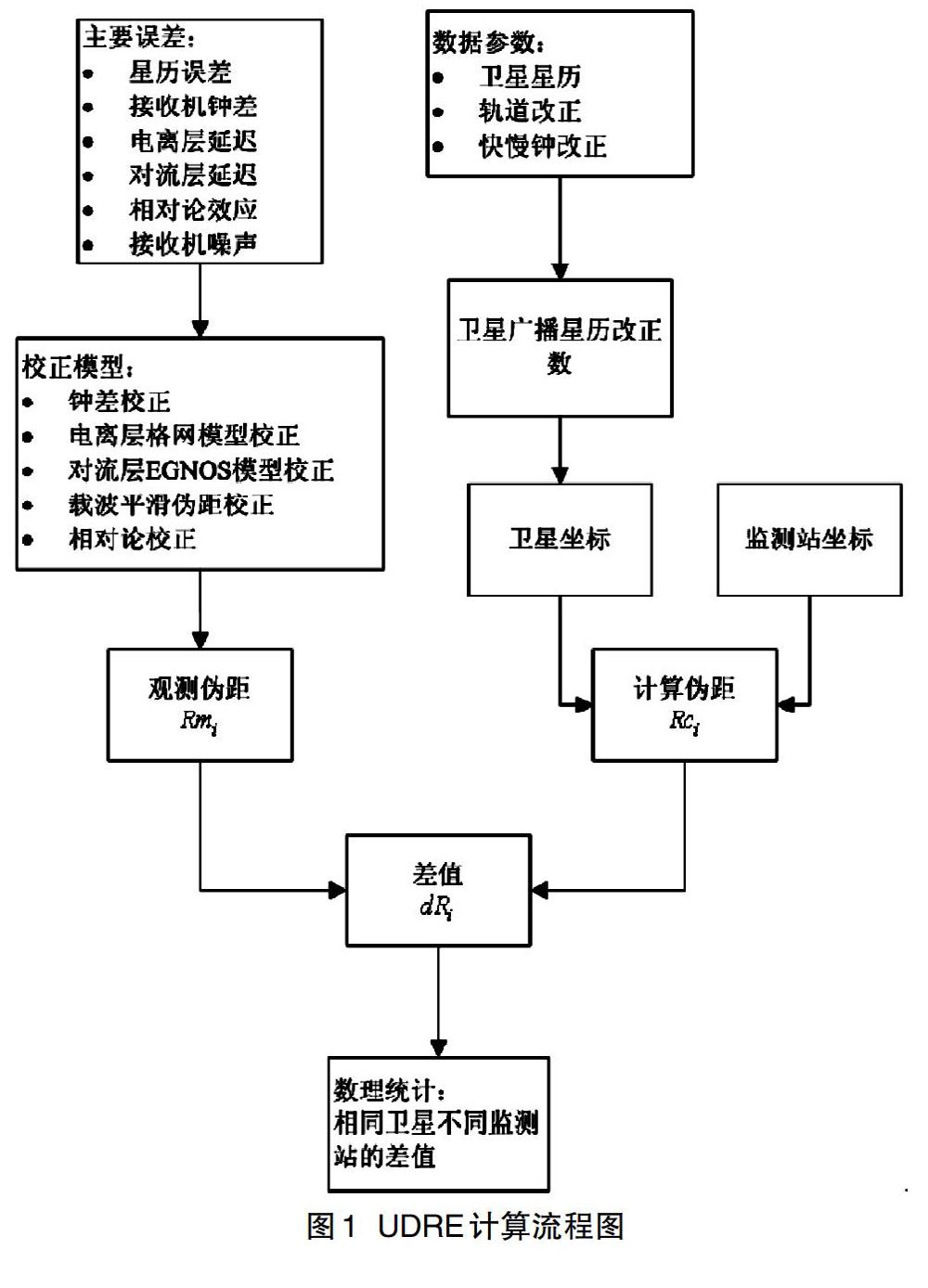
首先,利用单一卫星的观测伪距量与计算伪距量做差,再经过数理统计计算得到UDRE值。当UDRE值每秒更新一次时,空间段的GEO卫星每3秒便向用户端播发一次用户差分距离误差指数,而由用户差分误差指数判断出某个卫星的差分精度。地面段的监测站接收到的数据进行星钟误差校正、通过格网电离层模型对电离层延迟校正、对流层延迟校正等得到校正后,得到观测伪距量Rm。然后再通过GEO卫星播发的广播星历与卫星与地面监测站之间的相对距离,计算得出计算伪距量Rc,两者做差得到差值量dR; 最后,将地面段所有监测站对相同卫星的差值dRi做数理统计计算,得到UDRE值:
式中,为各个监测站对该卫星的伪距微分的均值,σdR为标准差;k(Pr)为3.2905,表示置信值为99.9%正态函数的分位数。
对于RURA的计算,当各项误差参数校正精度越高的时候,得到的UDRE值与RURA值越能够达到完好性性能的要求。同时对于UDRE与RURA值不宜过大,UDRE的最大可用为150m,RURA的最大可用值为300m[1-3]。如图1所示为UDRE计算流程。
2 实验结果
实验采用北京时间的2019年5月10日的下午2时到3时的时间间隔内,选定G4、G10号卫星进行实时的监测,使用Matlab对UDRE和RURA值进行仿真,实验结果如下所示:
图2、图3、图4和图5是G4卫星与G10号卫星的UDRE和RURA值的仿真图。在选取的10800个采样点中,G4卫星的UDRE最大约为3.79m,最小约为1.53m。RURA值在此范围内最大为3.80,最小为2.69m。G10卫星的UDRE最大约为2.80m,最小约为1.16m。RURA值在此范围内最大为2.82m,最小为1.68m。由仿真数据结果得出结论,仿真数据可出UDRE和RURA的数据都在1~4m的区间段,小于UDRE与RURA的最大可用值(UDRE为150m,RURA为300m),保证了北斗卫星导航完好性性能在航路过程中到终端进近的整个阶段全部可用。
3 结语
本文对于机载端完好性参数UDRE与RURA进行分析仿真,通过在格网电离层延迟的二次曲面拟合算法校正的电离层延迟,计算UDRE值,而得到的UDRE与RURA值均小于个字的最大可用值,且保证了北斗卫星导航完好性性能在航路过程中到终端进近的整个阶段全部可用。
参考文献
[1] 刘志远.北斗卫星导航接收机PVT算法的研究及实现[D].重庆:重庆三峡学院,2017.
[2] 张文峰,马绪瀛.北斗卫星导航系统性能评估[J].矿山測量,2014(04):40-43.
[3] 苏先礼.GNSS完好性监测体系及辅助性能增强技术研究[D].上海:上海交通大学,2013.

