基于遗传算法的家庭能源系统能量优化管理
郑晓坤 杨森 王海斌


摘 要:家庭能源系统是能源互联网的重要组成部分,文章针对家庭能源系统在并网模式下的能量优化管理问题,综合考虑各时段优化决策之间的联系,以系统长期运行经济效益最大化为目标,建立多时段动态优化模型。考虑到模型中存在的非线性互补约束以及多时段动态规划所导致的求解难点,利用遗传算法进行计算。最后根据实测数据建立仿真算例,验证了模型和算法的有效性。
关键词:家庭能源系统;多时段动态规划;遗传算法
家庭能源系统是能源互联网的重要组成部分[1],其能量优化管理是指通过合理控制系统各部分之间的能量使用而使系统运行最优。目前国内外学者针对家庭能源系统能量优化管理问题已经开展了一些有意义的工作,其中大部分研究以系统运行经济效益最大化为优化目标[2-3],在对时间的处理上,以1 h为单位时长,考虑一天或一周内的时间内系统运行方案,通过控制电池工作的状态来实系统中能量在各部分的分配,从而实现最大化经济化目标。本文以典型的家庭能源系统为研究对象,建立系统的运行管理模型,并以1 h为单位时长,通过控制系统在单位时段内的运行模式使系统24 h的运行经济效益最大化。本文最后利用仿真算例对模型进行验证,并利遗传算法求解模型中的动态规划问题。实现结果符合实际,支持模型的有效性。
1 家庭能源系统结构
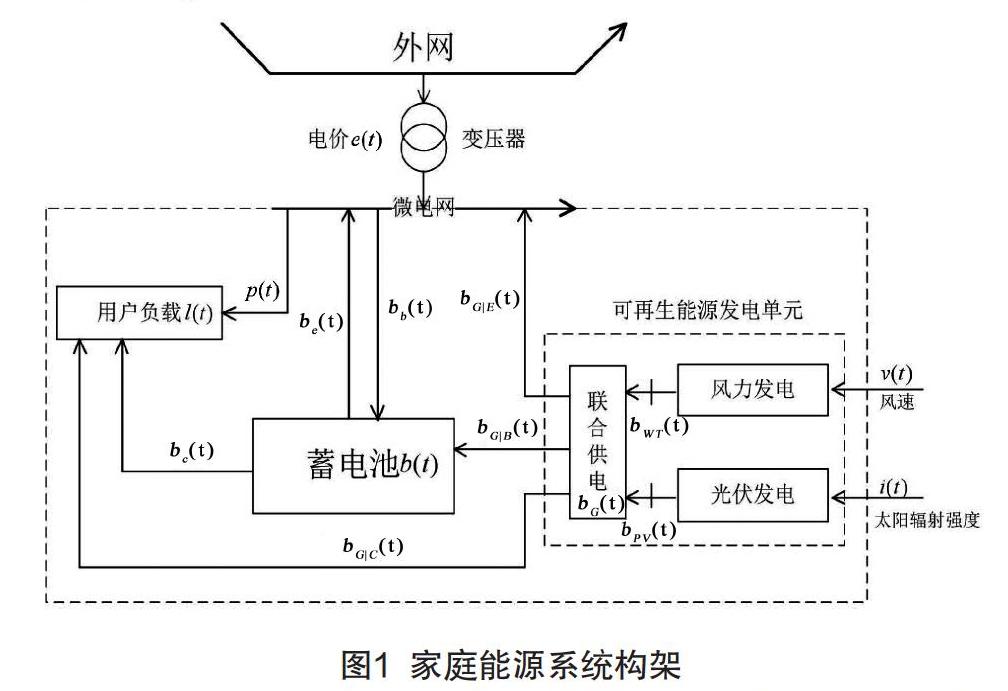
典型的家庭能源系统结构主要包括:局域消费者(用户负载)、可再生能源发电单元(风力发电单元和光伏发电单元)以及蓄电池。系统通过变压器连接到外网上,可以与外网进行电能交换,具体如图1所示。
在t时段(t=1,…,N)内风力发电单元产生的电量为bWT(t)≥0,光伏发电单元产生的电量为bPV(t)≥0。由于风/光具有互补性,一般将两种电能进行联合供电,故可再生能源发电量为bG(t)=bWT(t)+bPV(t)。
可再生能源发电单元在t时段输送给用户负载、蓄电池的电量分别为bG|C(t)和bG|B(t),在确定负载需求量得到满足时,可以将发电量向外网出售,售电量为bG|E(t)。
蓄电池向负载提供的实际电量为bC(t),负载从外网获得缺额电量p(t)。在t时段内蓄电池向外网实际出售的电量记为be(t)≥0,从外网实际购进的电量记为bb(t)≥0。
2 系统能量多时段动态优化模型
2.1 系统各部分运行模型
可再生能源发电单元由风力发电单元和光伏发电组成。风力发电模型和光伏发电模型引自陈长征等[4]研究内容。
建立蓄电池充放电模型时,选择蓄电池自放电系数为ε的充放电过程,并且考虑充放电过程中的电能损耗,则蓄电池的蓄电量变化模型为:
(1)
其中,b(t)表示蓄电池在t时段初始时的蓄电量,ηin表示电池充电效率,ηin表示电池放电效率。
2.2 约束条件
家庭能源系统运行约束一般从储能运行约束、发电单元运行约束以及网络约束3个方面来考虑,其中网络约束为:
l(t)=p(t)+bG|C(t)+bC(t)(2)
蓄电量在变化过程中应当始终满足电池容量的约束:
Emin≤b(t)≤Emax(3)
Emin表示蓄电池最低储电量,Emax表示蓄电池最高储电量。且蓄电池在充、放电时存在最大的功率_pch和_pdc,即蓄电池在各时段内的充、放电功率满足0≤pin(t)≤_pch,0≤pout(t)≤_pdc。考虑到储能在同一时刻不能既充电又放电,因此充放电形成一个互补约束,即pin(t)pout(t)=0。这是一个非线性的约束条件,引入该约束使得优化问题的非凸性很强,增大了问题的求解难度[3]。可再生发电单元的供电对象包括负载、蓄电池和外网,则需满足如下约束:
bG(t)=bG|E(t)+bG|C(t)+bG|B(t)(4)
上述约束条件分别根据负载、发电单元以及蓄电池的运行状态提出,在系统运行的每一时段都需要严格满足。
2.3 系统运行收益函数
系统在控制期内的运行收益为各个时段内的系统运行收益之和。而系统运行收益取决于系统与外网之间卖出(或购进)的电量。可以得到系统在控制长度为N的控制期T=t+s,(s=1,2,…,N)内,以获得最大经济效益为目标的目标函数为:
(5)
其中,e(t)为t时段市场电价。为了减小由于预测误差对系统全局决策带来的影响,这里对目标函数进行如下修正,γ为衰减系数:
(6)
其中,γ∈(0,1);随着预测步长s的增大,t+s时段收益的权重γs逐渐降低,因此可以减小由于预测长度增加带来的偶然误差。其中s=0,…,N,bWT(t+s)和bPV(t+s)分别表示根据t+s时段的风速和光照强度值得出的风力发电和光伏发电量。目前对于这类问题的求解大多應用遗传算法在全局范围内进行寻优,本文利用遗传算法进行模型的求解。
3 仿真结果分析
利用仿真数据模拟图1所示家庭能源系统在未来24 h内的运行状态,其中用户负载需求模拟如l(t)所示,结合风速和光照强度的历史数据,模拟出控制范围内系统各时段可再生能源发电量如G(t)所示。市场电价的变化规律如e(t)所示。并用遗传算法求出控制期内每一时段的能量优化策略。
家庭能源系统的各部分参数设定如表1所示。算法参数设置:迭代次数设为2 000,种群大小设为200,变异概率为0,均值μ进化步长为0.2,衰减系数r=0.9。实验结果:图2给出了算法的求解收敛过程,可以看出,在控制期内的最优经济效益为143.19元,实验结果符合经验规律。
4 結语
通过上述分析可知,本文提出的多时段动态规划模型能很好地根据系统各时段的状态,充分利用市场电价的变化信息,考虑各时段优化决策的联系,在全局范围内得出使系统整体运行最优的能量管理策略,能够在满足系统需求、提供安全稳定电量的基础上,最大限度地利用市场电价变化的价差,使系统运行实现最大经济效益。同时,文章利用遗传算法在求解该模型时能克服多时段动态规划问题的求解难点,还能解决由于互补性约束导致模型非凸的问题,实验结果验证了模型的有效性。
[参考文献]
[1]查亚兵,张涛,黄卓,等.能源互联网关键技术分析[J].中国科学(信息科学),2014(6):16-27.
[2]任建锋,丁亚伟,付磊,等.基于相位角原理的特高压电网失步解列改进方案[J].电力系统自动化,2011(10):104-107.
[3]吴建中,余贻鑫.最小化运行费用的时变重构全局优化算法[J].中国电机工程学报,2003(11):13-17.
[4]陈长征,王楠.遗传算法中交叉和变异概率选择的自适应方法及作用机理[J].控制理论与应用,2002(1):41-43.
Energy optimal management of a house-energy system
based on quantum genetic algorithm
Zheng Xiaokun, Yang Sen, Wang Haibin
(Chinese People s Liberation Army 78111 Troops, Chengdu 610000, China)
Abstract:The House-energy system is an important part of energy internet. This paper considers the link of all time intervals optimal energy management decisions of house-energy system under online pattern, and proposes a multi-period dynamic optimal model, including the corresponding objective function and constraints, which aims to maximize economic benefits for a long-term operation. Typically, the no-linear complementary constraints and multi-period dynamic programming problems are difficult to solve. Therefore, genetic algorithm is used to get the solution. Finally, a simulation example is illustrated using the measured data to test the model and algorithm. Experimental results show that our model are effective.
Key words:the house-energy system; multi-period dynamic programming; genetic algorithm

