基于深度卷积神经网络的红细胞识别算法研究

钟彩 彭春富 杜微 杨兴耀

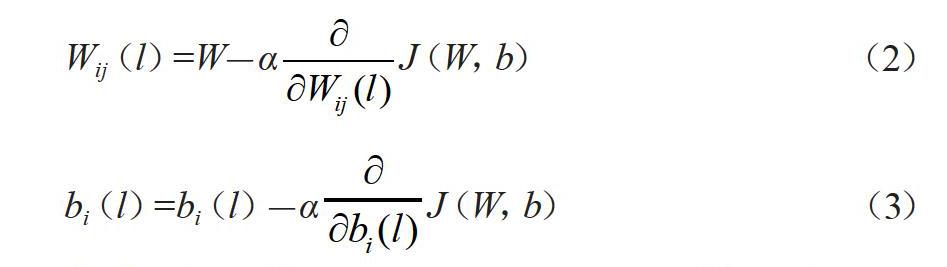
摘   要：针对深度研究的项目特点，文章对卷积神经网络结构的研究现状进行分析，总结卷积神经网络结构及优化算法。旨在通过对这些内容的分析，针对红细胞图像提取特征，设计群优化算法的卷积神经网络结构，以提高图像检测的科学性、准确性，展现深度卷积神经网络的识别算法技术的使用价值。

关键词：卷积神经网络;识别算法;深度研究

在人工智能技术发展中，深度学习作为较为重要的内容，改变了传统识别技术的使用状况，通过大数据资源的利用，展现深度学习模型中神经网络识别的价值。在图像识别技术运用中，其作为一种不同模式下的目标、对象研究技术，主要是通过计算机对图像进行处理，提高数据分析的整体效果。在以往的特征提取技术运用中，存在着一些局限性的问题，通过与卷积神经网络（Convolutional Neural Networks， CNN）模型的融合，可以在梯度下降方法使用中进行各项数据参数的训练，并实现对图像以及参数的分析，展现深度分析的价值。因此，在当前人工智能技术中，运用卷积神经网络的识别算法，可以提高图像识别的整体效果。

1    卷积神经网络结构研究现状

卷积神经网络模型算法主要由多个卷积层、下采样层和全连接层组成，每一次的输出是对原始输入的一组特征表示。其中在卷积层，通过一个卷积核对来自上一层的特征图进行卷积，然后通过一个激活函数得到卷积层的输出特征图，激活函数使用sigmoid函数。下采样层将上一层的特征图进行下采样加权和偏置得到该层的输出特征图[1]。

卷积神经网络主要采用局部感知区域、共享权值以及空间域上的降采样，对位移、缩放等状态进行研究，该种分析方法具有稳定不变的特点，研究中，针对细胞图像特征值提取的项目特点，对卷积神经网络结构使用方法进行分析，由于在红细胞定位过程中，可能有一些杂质掺杂进来，为了区别这些杂质（本项目统称为非红细胞），需要对红细胞进行特征提取。

2    卷积神经网络结构及优化算法

2.1  卷积神经网络概述

卷积神经网络作为一种多层次神经网络结构，通过对图像分类以及识别算法的运用，逐渐形成了深度学习的模式，其作为前馈神经网络形式，可以充分满足识别技术的使用需求。在卷积神经网络中，通过人体设计感受机理的分析，会提高识别技术的使用效率。例如，在人体神经元系统中，神经元感受视野是在视网膜的特定区域中形成的，通过卷积神经网络才可以刺激神经元活性，提高识别算法使用的整体效果。

卷积神经网络与普通神经网络存在区别，主要由卷基层、子采样层构成，在卷基层中，通过神经元与部分邻层神经元的连接，可以形成同一特征的平面神经元共享权值，提高识别计算的整体效果。卷积神经网络技术凭借自身优势被广泛地运用在语音识别、人脸识别、运动分析、自然语言处理以及脑电波分析等领域之中。

2.2  卷积神经网络结构

2.2.1  卷积神经层

在卷积操作中，其主要是将图像以及滤波矩阵作为内积，主要目的是通过稀疏连接、权值共享以及采样等方法，得到某种程度的位移、初度及形变。在图像处理中，需要在系统中输入width×height区域的大小数据，之后按照固定权重的卷积核形成二维数据，具体操作中，需要与矩阵上对应位置移动状态进行分析，形成一种覆盖性的图像，直到矩阵移动完成之后得到特征图矩阵。在卷积神经层中，卷积核越大，相关参数的处理效果越高，但是若遇到训练参数多、卷积核小的问题，应该保持训练参数的精确性，为多层数据的处理以及分析效果的强化提供参考[2]。

2.2.2  ReLU激励层

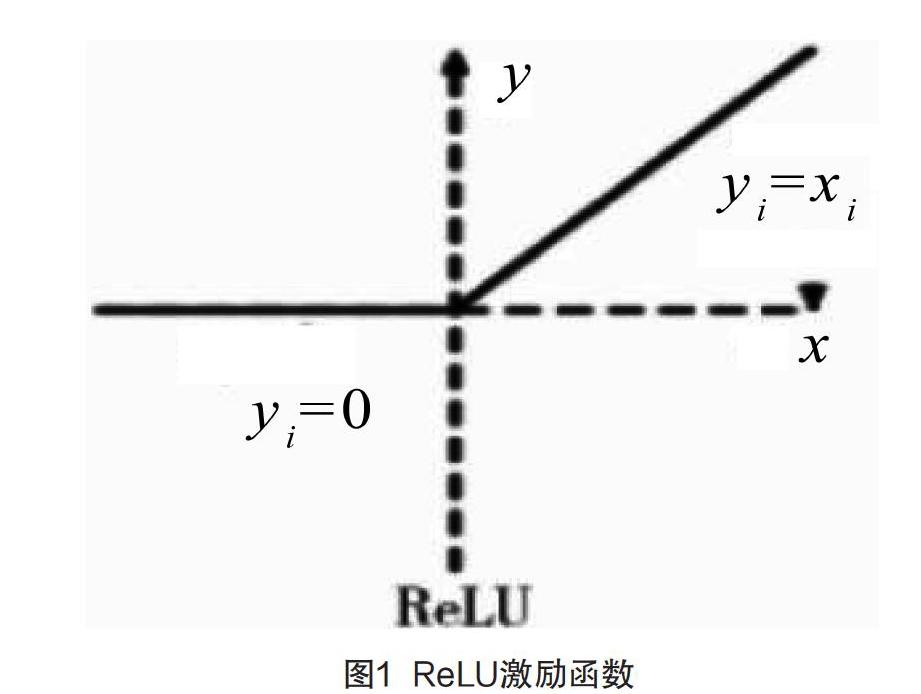
对于规范性的ReLU激活函数，具体函数变化如图1所示。具体的表达公式为（1），当输入x>0时，输出值为x;若输出的数值≤0，输出的结果为0。

y={0，max（x）}     （1）

在红细胞图卷积神经网络系统中，通常会使用ReLU激励函数代替sigmoid函数。在ReLU激励层中，当所输入的数值x>0時，ReLU函数导数为恒定状态，但是sigmoid函数不是恒定的。也就是说，在ReLU函数中，可以避免其他函数两端接近目标的问题，在导数变小的状况下，会使训练神经网络出现反向传播的现象。在ReLU函数分析中，该种方法可以实现数据获取快、求梯速度简单。

2.2.3  池化pool层

池化层作为空间下采样层，一般会在卷基层之后，通过图像卷积将polling小领域内特点进行整合，从而形成一种全新的特征。同时，pool层也被称为降采样层，该计算方法不仅可以达到降维的目的，而且也会降低卷基层的输出维度，避免卷积输出的误差现象[3]。

2.3  反向传播梯度下降算法

在红细胞神经网络参数计算中，通常会使用随机梯度下降法，其核心目标是掌握最优化的权重参数（W，b），将损失函数值控制在最小的状态。参数更新的关键是掌握损失函数对各项权重参数导致的分析，因此，在梯度下降法计算中，公式如（2—3）。

Wij（l）=W-αJ（W，b）     （2）

bi（l）=bi（l）-αJ（W，b）     （3）

公式中的α是学习速率;Wij（l）是第l+1层的第i个神经元以及低l层的第j个神经元相互连接的权重参数;bi（l）是第l+1层的第i个神经元的偏置项。

在实际训练的过程中，应该对学习率进行合理选择。在反向传播算法使用中，通过向前传播计算，可以对每层网络的激活数值进行传输，之后按照每个层级的输入节点，进行残差计算[4]。