70MPa车载氢系统框架随机振动与疲劳寿命分析

王荔

摘 要：近年来，燃料电池汽车由于零排放零污染逐渐走入大众视野，而氢系统则是燃料电池汽车的重要组成部分，氢系统的经济性与安全性是制约燃料电池汽車发展的关键因素，所以对氢系统结构疲劳寿命分析与优化格外重要。本文通过对某车型项目70MPa氢系统框架进行基于功率谱密度的随机振动分析，发现其结构强度薄弱部分，进而对结构进行优化。振动分析完成后通过疲劳分析，对优化后的结构做最终校验并评估疲劳寿命。本文总结出一种适用于70MPa氢系统框架的随机振动疲劳分析方法，对氢系统结构设计开发具有指导意义。

关键词：氢系统框架;随机振动;结构优化;疲劳寿命

1 前言

随着国家可持续发展战略目标的提出，环境友好和低碳排放理念在各个行业的不断深入，同时最近几年氢能等绿色能源与氢燃料电池汽车也得到了前所未有的较快发展。目前国内的燃料电池汽车储氢压力以35MPa为主[1]。如果采用70MPa储氢压力可在同等容积下大幅度提升储氢量和续航里程。对于布置空间有限的乘用车而言，70MPa轻质车载氢系统的应用具有很高的科研价值和广阔的市场前景。

由于燃料电池汽车在国内属于较新的领域，所以目前对氢瓶框架进行随机振动疲劳分析的单位及学者很少。大连理工大学陈立[2]对用Q235钢制作的钣金件氢瓶固定架根据所采集的路谱进行了详细的随机振动分析，然后根据雨流法及材料S-N曲线估计其寿命;北京天海公司刘智勇等[3]根据GB/T 4857.23对铝氢瓶框架进行随机振动分析，但是其功率谱密度为公路运输包装件所用试验工况，与传统汽车行业国标规定的功率谱密度相比偏小，虽有随机振动仿真分析但没有进行疲劳寿命的评估;清华大学樊斌等[4]仅对氢瓶进行了疲劳寿命评估及有限元仿真分析。

本文采用有限元的方法对铝镁合金储氢系统框架首先进行模态分析，得到框架模态，然后根据某整车厂提供的功率谱密度进行分析研究，总结出一种适用于70MPa储氢框架振动疲劳寿命的分析方法，为储氢框架的设计、优化提供指导。

2 氢瓶框架模型

2.1 氢瓶框架模型

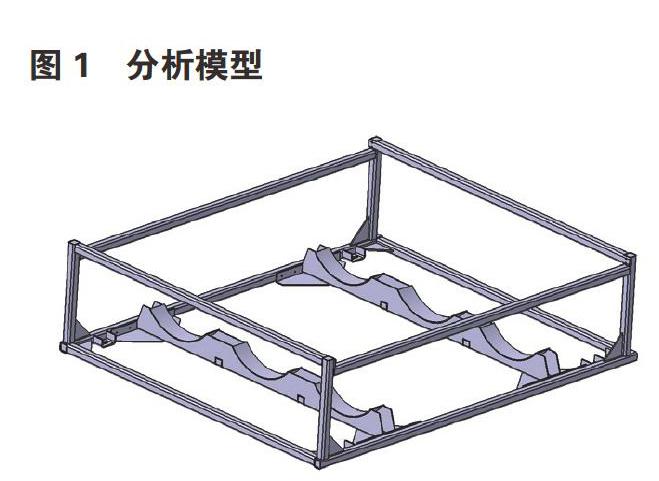
氢瓶固定架采用铝方管及铝板结构焊接成型。其中，氢瓶固定板与框架为螺栓连接，氢瓶固定支座与固定板为焊接。分析模型如图1。

2.2 有限元模型建立

由于模型所用材料是铝合金板，其在厚度方向尺寸远小于长度、宽度方向的尺寸。所以采用壳单元shell181分析。shell181单元为4节点单元，使用一次位移插值函数，是适用于线性分析与大转角大应变的非线性分析的低阶单元[7]。

对框架各结构划分网格。由于只关注氢瓶框架及氢瓶固定板强度，所以在保证分析精度的前提下对其他相关结构进行简化处理。简化处理如下：

1）将氢瓶简化为质量点，作用在氢瓶安装支座上面，简化氢瓶固定带安装结构。

2）忽略非支撑结构，如氢瓶阀等供气零部件。

3）取消非受力部分的圆角。

单元边长3-5mm，网格数量174760，节点数量174947，划分网格后模型见图2。

2.3 材料参数

储氢框架材料为6061-T6，所用材料参考GB/T 3880-2012进行材料力学拉伸性能测试。

测得主要参数见表1：

材料真实应力应变曲线，如图3所示。

3 随机振动分析

3.1 理论基础

随机振动分析，即随机载荷作用于确定结构所得到的响应，也称功率谱密度（PSD）分析。功率谱密度函数（PSD）可用于表示频域信号表征的随机激励载荷。随机激励下的响应是统计意义下描述的响应，在任何瞬时响应具体大小未知，但其大小的概率可以给出。均方根应力即RMS应力，以及其响应的功率谱密度振动分析结果主要关注对象。由PSD随机振动分析，可以得到统计学范畴下的X、Y、Z三个方向所对应的1σ、2σ、3σ应力。三个解服从标准正态分布，1σ应力出现的概率为68.31%，2σ应力出现概率为27.1%，3σ应力出现概率为4.33%。三个解出现概率覆盖99.74%。

对模型进行模态分析是随机振动分析步骤一，然后采用模态叠加法进行第二步的单位激励的频响分析。通过频响分析得到频响函数，根据加速度功率谱密度，可输出响应的功率谱密度以及响应的均方根值[5]。一个线性系统，承受平稳的随机载荷，其PSD为SX（ω），响应信号为y（t），其PSD为Sy（ω），则y（t）的功率谱密度可以用下式计算：

3.2 分析过程

各种复杂路况会引起在汽车在实际行驶过程中的颠簸振动。所以有必要对氢瓶框架进行基于真实路况功率谱的随机振动分析。对于车载结构的随机振动问题，目前国内对传统汽车及锂离子电池新能源电动汽车有相应的国家标准[8]，而针对燃料电池汽车储氢瓶框架安全性能的考核，目前还没有相应的国家标准，本文借用国标GB/T 31467.3-2015《电动汽车用锂离子动力蓄电池系统安全性要求与测试方法》中规定的随机振动试验方法对氢瓶框架按规定的功率谱密度进行随机振动分析。

本文通过有限元分析软件设置三个分析步：

1）模态分析。对储氢瓶系统框架固定四个与整车安装点，进行模态分析;模态分析关注前十阶振型与固有频率。

2）频响分析。根据模态分析数据，在四个安装点施加单位加速度激励。

3）随机振动分析。通过模态分析得到的结果以及频响分析得到的传递函数进行基于功率谱密度的随机振动分析，输出RMS1σ应力。

3.3 模态分析结果

模态分析得到的固有频率与振型可以为整车动力性能的设计提供参考，避免整车与氢瓶框架系统共振，影响车辆行驶安全及车辆舒适性。

模态分析得到前五阶固有频率及振型见表2，图4-图8;

由振型图可以看出，前三阶模态中一阶模态为框架的整体扭转模态，二阶模态为鞍座弯曲模态，而三阶模态为局部模态。

3.4 随机振动分析结果

对模型X、Y、Z三个方向在GB/T31467.3中所规定的功率谱密度下进行随机振动分析。分布得到X、Y、Z三个方向的RMS应力均方根值云图。见图9，图10，图11。

由云图可以得到X方向最大RMS应力为114.2MPa，位于氢瓶框架与氢瓶固定板螺栓连接处。Y方向最大RMS应力为162.0MPa，位于氢瓶与鞍座相连焊接位置。Z方向最大RMS应力为159.5MPa，位于氢瓶遇鞍座连接处。

3.5 分析结论

由随机振动分析得到三个方向的1σRMS应力最大值为Y方向的159.5MPa，则最大3σ应力为478.5，则由式（3）得到：

478.5MPa>σs=277MPa

即判断该结构不满足随机振动强度要求。

4 结构优化及分析

4.1 结构优化

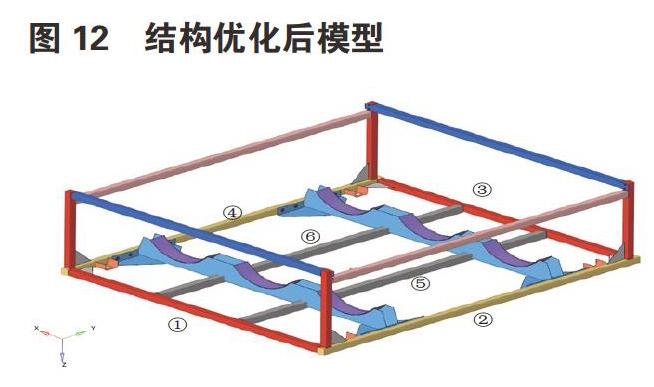
上述分析中，随机振动RMS应力大于材料的屈服强度，所以在实际振动中，出现材料破坏的概率很大。从应力云图可以看出，X向即1、3号梁长度方向应力较低，而Y、Z方向框架承受应力较大，在材料不变前提下，考虑在Y向增加5、6号横梁以加强框架的整体刚度性能并降低局部RMS应力，优化后模型如图12。

4.2 优化结果

4.2.1 模态分析

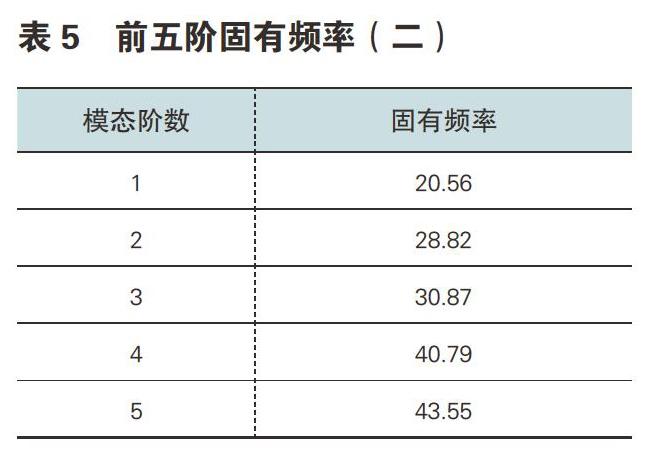
优化后，对结构进行模态分析，得到前五阶模态如表5，图12-16：

优化后前五阶模态中，一阶模态固有频率20.56比优化前结构一阶固有频率12.15提高40%，即模型结构刚度有较大提升。

4.2.2 随机振动分析结果

对优化后的机构进行随机振动分析，分析过程不变。得到三个方向的RMS云图如图13-15：

由随机振动分析可以得到，X方向的最大RMS应力分别为15.06MPa，位于上层支架螺栓连接处;Y方向的最大RMS应力分别为17.37MPa，位于安装支撑板与4号梁螺栓连接处;Z方向的最大RMS应力分别为18.32MPa，位于框架与整车安装支架处。即最大RMS3σ为54.96MPa。取安全系数1.35，则：

54.96×1.35=74.2MPa<σs=277MPa

可认为，在99.73%的概率下，该结构可以满足GB/T31467.3-2015中所规定的试验要求。

5 疲劳分析

工程经验认为结构最大RMS1σ应力小于材料拉伸极限的20%，即可认为具有无限寿命，本文分析的结构中最大RMS1σ应力为18.32MPa，小于材料拉伸极限的20%即63.8MPa，为了验证工程经验是否正确，对结构进行随机振动疲劳寿命分析。

5.1 分析方法

本文采用工程上应用较广泛的Miner线性累积损伤理论[9]，结合材料S-N曲线，应用三区间法估算框架的疲劳寿命[10]。

5.2 分析过程

计算步骤如下：

1）估算危险点处的平均应力频率V0+;假设结构期望寿命T0=4×106次，振动平均频率V0+=5Hz

2）根据随机振动结果得到1σ、2σ、3σ应力，查材料S-N曲线得到T1σ，T2σ，T3σ;

由文献[11]查得材料6061-T6的S-N曲线如图16、17。选取图中平均应力为0的应力曲线。

查图16，17得：

当RMS1σ=18.32MPa，N1σ→+∞

当RMS2σ=36.64MPa，N2σ→+∞

当RMS3σ=54.96MPa，N3σ≈1.2×106

3）根据式4估算出框架的循环次数即寿命。

由式4得到：

即求得疲劳寿命为554万次，损伤为0.722。

6 结论

本文通过有限元软件，对70MPa储氢系统进行基于功率谱密度的随机振动分析，得到了在三个方向的功率谱的激励下，框架三个方向的1σRMS应力值，并通过随机振动的RMS应力值进行疲劳寿命的估算，为其他同类型的氢瓶框架的随机振动计算及疲劳寿命分析计算提供参考。通过分析可以得到以下结论：

1）随机振动最大处位于氢瓶固定板与氢瓶框架螺栓连接位置，最大RMS应力为18.32MPa，在Z方向激励时产生。最大RMS3σ为54.96MPa，小于材料屈服极限。所以该70MPa储氢系统结构强度符合要求。

2）分析得到疲劳寿命为554万次，其累计损伤值为0.722，损伤值远小于1，疲劳寿命满足期望寿命，所以该70MPa储氢系统寿命符合要求。

3） 根據工程经验得到的1σRMS应力值小于拉伸强度的20%，即可认为结构具有无限寿命在本次分析中得到验证，可以应用在以后的工程项目中。

基金项目：国家重点研发计划资助（2018YFB0105500）。

参考文献：

[1]张新健. 燃料电池汽车车载氢系统安全性分析[J]. 时代汽车，2019，305（02）：100-102.

[2]陈立. 车用纤维全缠绕氢瓶固定架的疲劳分析与优化[D]. 大连理工大学，2013.

[3]刘智勇，李晓峰，朱冰冰，et al. 基于功率谱密度的两瓶组车载供氢系统随机振动分析[J]. 包装工程，2019，40（01）：79-84.

[4]樊彬，赵雨东，陈海红. 燃料电池城市客车用储氢瓶有限元分析和疲劳寿命分析[J]. 汽车技术，2013（01）：7-11.

[5]孟凡涛，胡愉愉，MengFanTao，et al. 基于频域法的随机振动载荷下飞机结构疲劳分析[J]. 南京航空航天大学学报，2012（1）.

[6]（美）饶（Rao，S，S）著;李欣业，张明路编译. 机械振动[M]. 清华大学出版社，2009.

[7]贺李平，肖介平，龙凯. ANSYS 14.5与HyperMesh 12.0联合仿真有限元分析[M]. 机械工业出版社，2014.

[8]苏阳，杨涛，鄂世国，et al. 电动车电池包振动疲劳分析[J]. 汽车实用技术，2016（2）：109-110.

[9]Zheng M ，Shen F ，Luo P . Vibration Fatigue Analysis of the Structure under Thermal Loading[J]. Advanced Materials Research，2013，853：559-564.

[10]潘红明. 基于三区间法的高速动车组齿轮箱体疲劳寿命研究[D].2016.

[11]Yahr G T . Fatigue Design Curves for 6061-T6 Aluminum[J]. Journal of Pressure Vessel Technology，1997，119（2）：211-215.