七自由度登高平台的逆运动学求解

吴静远 许沛森 畅远

摘 要：针对七自由度登高救援平台机械臂，介绍了一种基于雅可比矩阵伪逆的逆运动学求解方法：综合速度加权最小范数法与阻尼最小二乘法，实现冗余自由度机械臂运动过程中规避关节限位，保证奇异位置附近求解稳定性的要求。同时在该算法中引入闭环理念，保证较小的求解误差。

关键词：七自由度冗余机械臂;伪逆;加权最小范数法;阻尼最小二乘法

中圖分类号：TP242.6 文献标识码：A 文章编号：1671-2064（2020）01-0216-02

1 建立臂架的正运动学方程

1.1 齐次变换矩阵的建立

臂架的正运动学方程采用D-H参数法获得。首先，在各个关节上定义D-H坐标系，描述当前各关节的空间姿态，利用齐次变换矩阵可获得相邻臂架的位姿关系，最后得到每个关节相对于基坐标系的空间位姿变换。

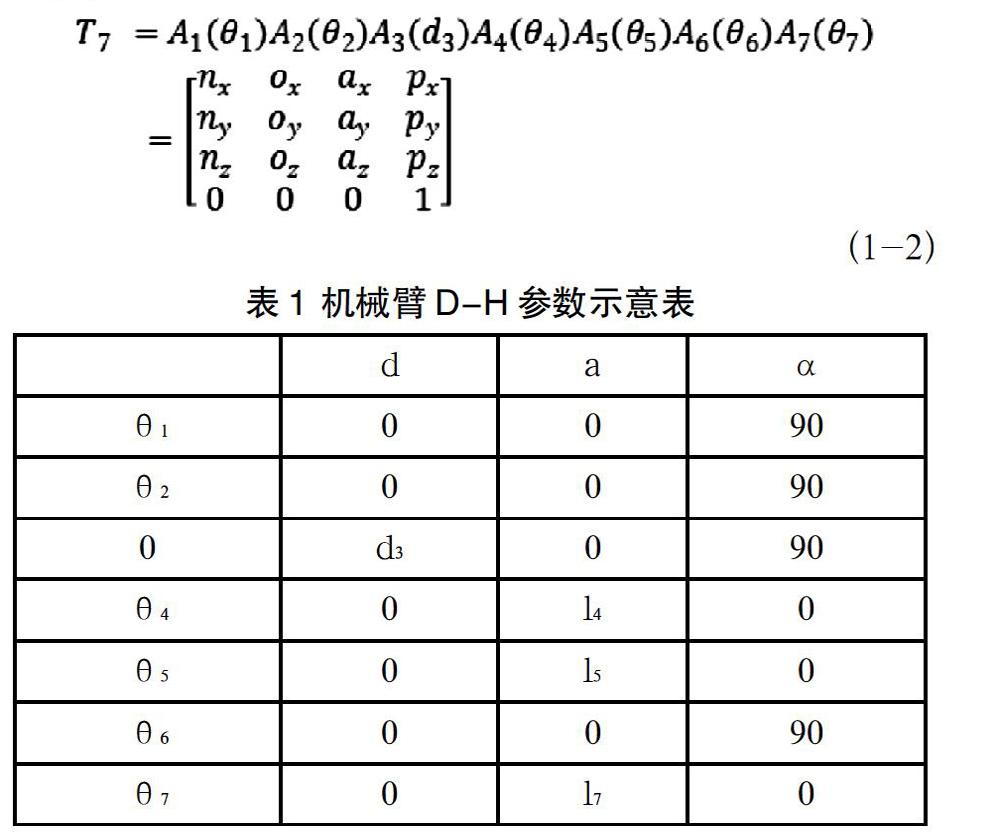
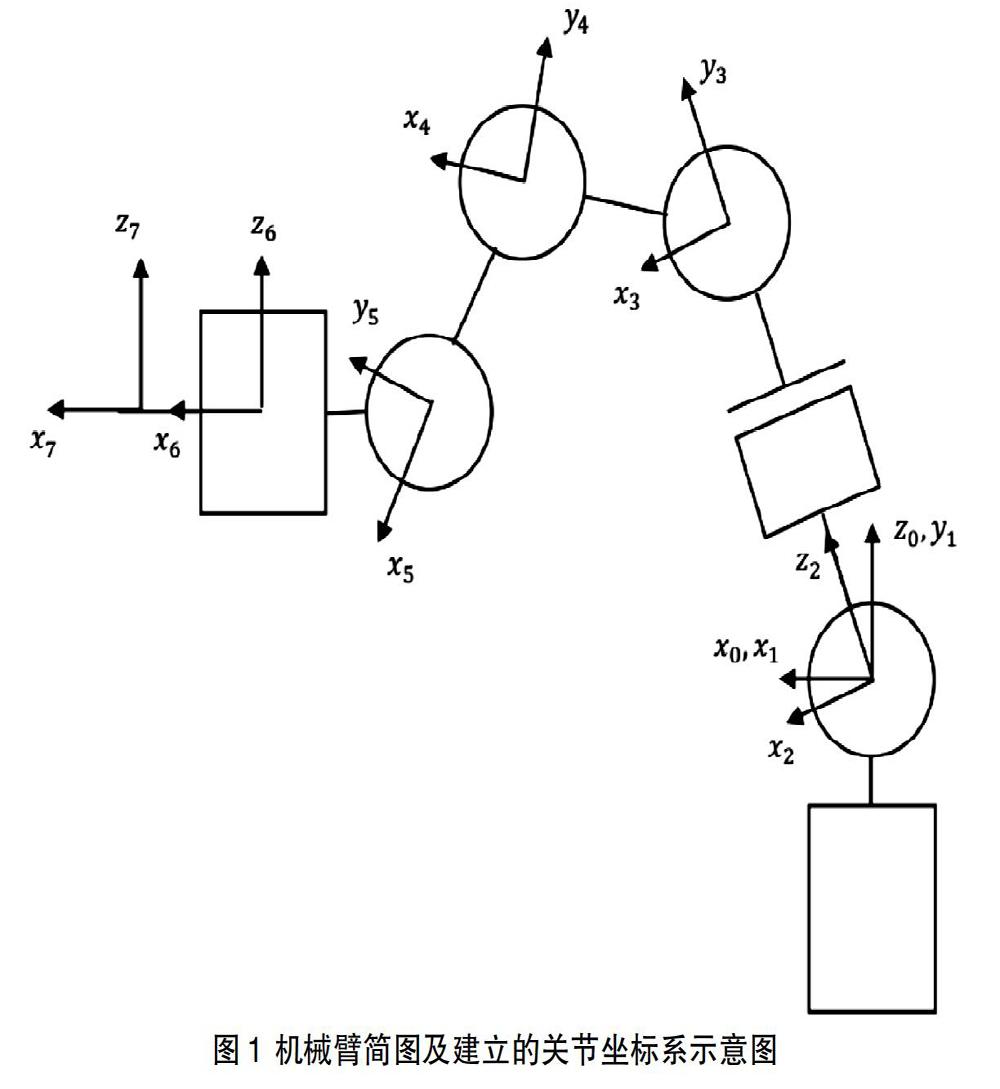
参考机械臂架构，对各部件按照连接方式进行简化。臂架标号从原点到末端载人平台为0，1，2…7，简化模型如图1所示，D-H参数见表1所示。

采用D-H法对机械臂进行运动学建模，第i个连杆对第i-1个连杆的坐标齐次变换矩阵如式（1-1）所示：

（1-1）由此得到该七自由度机械臂的正运动学模型如式（1-2）所示：

1.2 雅可比矩阵的建立

本文采用微分变换法计算机械臂的雅可比矩阵[1]。

随着关节变量接近极限值，O（h）的值增加，在关节变量到达极限值时为无穷大，当在关节限制范围内运行时，几乎为0，当关节变量靠近极限值时其值为无穷。

当关节变量向限位值变化时，权重系数逐渐增大，关节运动速度减小，当关节变量趋向极限值时，权重系数趋向于无穷大，关节运动几乎停止。

3 结语

本文介绍了一种基于雅可比矩阵伪逆结合了加权最小范数法，最小阻尼二乘法的闭环逆运动学求解算法。该算法通过加权最小范数法实现了规避关节限位，通过阻尼最小二乘法保证了在奇异位置的求解稳定性。该算法的闭环结构确保误差较小且具有收敛性。

参考文献

[1] 梁西昌.救援机器人冗余液压机械臂运动学分析及轨迹跟踪控制方法研究[D].山东：山东大学机械工程学院，2018：60.