基于对流-导热耦合模型的寒区水工隧洞围岩温度场分布规律研究

孟 尧， 姜海波

(石河子大学 水利建筑工程学院， 新疆 石河子 832000)

1 研究背景

高海拔寒区隧洞贯通后在自然通风条件下隧洞内部出现空气对流，在寒区周围环境温度较低，隧洞围岩能使得洞内温度高于洞外温度，冷空气进入隧洞内发生强烈热交换，从而影响寒区隧洞围岩的温度场。因此必须对自然通风条件下的对流-导热进行深入研究。由文献[1]可知空气温度和空气流速是影响隧洞内温度场的主要因素，因此主要研究隧洞内风速、风温对隧洞温度场的影响。寒区隧洞的安全稳定离不开对隧洞温度场的分析，目前，关于寒区隧洞围岩的温度场已取得许多研究成果。

刘杰等[2]对比分析了引水隧洞不同洞型开挖的应力场分布和塑性区分布，从稳定性考虑，确定圆形断面为最优开挖断面。周小涵[3]验证了圆形断面的适应性，根据理论分析，建立隧道围岩、衬砌和气流的对流-导热耦合圆形断面模型，完成了通风条件下温度场的完整计算，并且与寒区隧道现场测试的温度场进行了对比分析。许增光等[4]基于热传导方程，建立了岩体与裂隙水流热量交换下的温度场数学模型，采用有限单元法求出数值解。张学富等[5]根据相关的基本理论，建立了空气与围岩对流换热的三维围岩温度场计算模型，并且对青藏铁路风火山隧道空气与围岩对流换热问题做出了三维非线性分析，其研究成果对空气与围岩对流换热系数研究有参考意义。韩斐等[6]采用灰色关联度分析方法得到不同影响因素与对流换热的关联程度，其中风流速度的关联度最大。何春雄等[7]考虑了隧洞所在的环境，以及围岩参数等条件，分析了隧洞内两种空气流态下气温的分布规律；根据气温得到围岩温度场的温度数据，然后模拟计算出隧道围岩温度场的分布规律。王玉娇[8]利用相似理论建立试验台，得出不同工况下的矿井巷道围岩与风流传热的温度场，拟合出了对流换热系数的计算公式。Bonacina等[9]分析得出相变的一维非线性方程，提出了相变热传导温度场的数值求解方法。Comini等[10]分析得出一种适用于非线性物理属性与边界条件瞬态传热问题的方法，通过模拟研究得出相变条件非线性热传导的温度场分布规律。何春雄等[11]建立了隧道内空气与围岩对流换热和固体导热的综合模型，分析预报了祁连山区隧道的温度和围岩冻融状况。刘胜等[12]、马凤伟[13]和高焱等[14]研究了外界条件对隧道围岩温度场的影响，得出隧道围岩温度场受外界气温、通风、地形影响，随时间呈周期性变化。郝飞等[15]采用ANSYS有限元软件，模拟分析了寒区隧道的温度场，将计算得出的温度场数据与实测的温度数据进行对比。徐鑫[16]主要以理论分析和数值模拟为主，模拟分析通风条件下寒区隧道围岩及衬砌温度场的变化规律。陈建勋等[17]、孙克国等[18]、肖兴民[19]和韩跃杰等[20]研究了不同作用下寒冷地区隧道纵向和径向围岩温度场，得出两个方向温度的变化规律。杨旭等[21]分析预测了季节性冻土区隧道温度场，可有效地防止隧道的冻害，提出在同类型隧道有限元计算中，初始边界温度应以实测温度资料来确定。以上研究分析了隧洞外界环境和围岩特性对隧洞温度场的影响规律，建立了对流换热模型，并且采用不同方法分析得到对流换热的主要影响因素。因此本文结合上述研究成果详细分析气流、围岩和围岩之间对流-导热模型中自然通风风速和风温对寒区隧洞围岩温度场的影响。

在高海拔寒冷地区，水工隧洞围岩的物理力学性质、性能演化具有内在的热力学机制与变化模式。寒区水工隧洞围岩力学性能的演化主要来自复杂的环境因子，例如环境温度变化、自然通风温度、风速等。在长期的低温场作用下，围岩力学特性会发生不同程度劣化，影响水工隧洞的稳定及安全运行。因此，有必要研究不同的环境条件下水工隧洞温度场的特性及其演化规律。本文以新疆某水工隧洞为依托，基于现场监测数据，采用有限元软件数值模拟的方法，对寒区隧洞在通风条件下的对流-导热展开模拟研究。确定气温与隧洞围岩的传热参数及模型，定量分析计算寒区隧洞内温度场的分布规律及其变化规律，研究隧洞内风速、风温对寒区隧洞围岩温度场的影响，并分析其影响机制，可为寒区水工隧洞的安全运行提供理论基础。

2 高海拔寒区水工隧洞围岩温度现场监测

2.1 工程概况

新疆某引水隧洞全长20.14 km，位于高寒半干旱气候区，季节性温差较大，年最低气温-34.3℃，最高气温35.9℃，最冷月平均气温-16.66℃；多年平均风速2.1 m/s，风向为W。多年平均封冻天数96 d，历年最长结冰期190 d。最大积雪厚度16 cm，最大冻结深度235 cm。根据现场监测得知，引水隧洞围岩的实测温度为9℃。洞址区为第四系地层，未见层理，洞室围岩完整性较好。通过地质勘查，隧洞区只有少量上层滞水，围岩及周围岩体水分较少，可以忽略水分对温度场的影响。

2.2 监测内容和方案

为了研究寒区隧洞温度场分布规律以及预防隧洞发生冻胀破坏，2017年1-2月份对隧洞围岩进行温度监测，同时也对隧洞结冰点进行统计。温度监测分为大气温度和洞内气温，洞内气温是监测洞壁围岩温度。根据现场勘查结果，隧洞进出口段易出现冻胀结冰，选取距离洞口1 000 m范围作为监测对象。将1 000 m长的隧洞划分成10个区间，选取每个区间的中点作为监测断面，测量每天10：00、12：00、14：00、16：00这4个时间点的温度值，以进口方向为基准，对监测断面进行编号，共10个监测断面。隧洞围岩温度监测平面布置如图1所示。

2.3 监测结果分析

实际工程在2017年1-2月监测的日平均洞壁温度监测数据如表1所列。

图1 隧洞围岩温度监测断面平面布置图(单位：m)

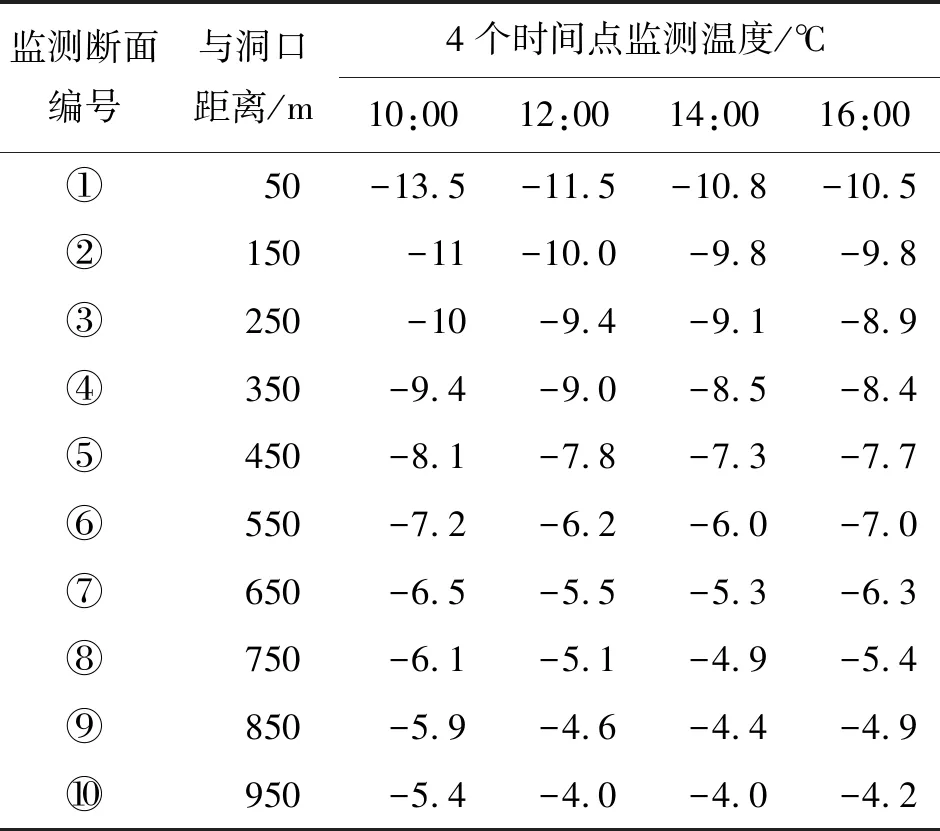
表1 洞壁温度监测数据

由表1可以看出，10：00洞口150 m处的温度比50 m处的高2.5℃，升高幅度为18.52%；250 m处的温度比150 m处的高1℃，升高幅度为9.09%；350 m处的温度比250 m处的高0.6℃，升高幅度为6.00%。

以上数据可以看出随着与洞口距离的增加，洞壁围岩温度在逐渐升高，并且升高的幅度在减小。监测点①从10：00到12：00温度升高2℃，从12：00到14：00温度升高0.7℃，从14：00到16：00温度升高0.3℃；监测点③从10：00到12：00温度升高0.6℃，从12：00到14：00温度升高0.3℃，从14：00到16：00温度升高0.2℃。以上数据可以看出早上10：00到下午4：00外界气温逐渐升高，隧洞监测点的温度也随之升高，距离洞口越远的监测点温度受外界气温的影响越小。

3 高海拔寒区水工隧洞围岩温度场数值模拟

3.1 对流-导热耦合模型

3.1.1 对流换热 计算流体与固体壁面接触换热用牛顿冷却公式表达：

q=h(Ta-Tb)

(1)

式中：q为单位传热面积热流量，W/m2；h为物体与周围介质的对流换热系数，W/(m2·℃)；Ta为物体的壁面温度，℃；Tb为介质的平均气温，℃。

3.1.2 导热 热传导用傅立叶导热基本定律表达：

(2)

式中：n为等温面法线方向。

3.1.3 初始条件与边界条件 初始瞬时时刻，物体的温度表示为：

T(x,y,0)=T0(x,y)

(3)

一般情况下T0为常数。

边界条件，即对流换热边界条件，表示为：

(4)

模型中假定：(1)隧洞围岩是连续均质的并是各向同性的，隧洞内气流为连续介质；(2)围岩的原始温度沿隧洞轴向和径向不变；(3) 隧洞壁面的换热条件是一致的，沿隧洞轴向和径向不发生变化。

3.2 有限元计算模型及参数

为了更好地研究高海拔寒区空气与围岩的对流，本文根据实际工程所在的地形建立山体平面模型，洞径为3 m，长度为1 000 m的隧洞，由于隧洞很长所以只需要对一些特殊点位的温度分布进行分析，如：距离进口10 m处的断面、距离进口40 m处的断面、距离进口400 m处的断面、距离进口990 m处的断面。这些都是洞口处和隧洞中间部分的点位，具有代表性。通过计算分析这几个点位得出风温、风速对围岩温度的影响规律，从而就能得出整个隧洞围岩温度场的变化规律。平面模型如图2所示。

图2 隧洞平面模型

隧洞周围的围岩初始温度场为恒定值，根据文献[21]取实测温度值9℃。由于模型内边界为通风边界，空气和围岩发生对流换热，因此为对流换热边界条件。通过工程附近气象站的温度监测数据可知11月-次年3月份共150 d的风温，通风初始温度为4℃。

由参考文献[8]可知：当风速为1 m/s时，h=39.96 W/(m2·℃)；当风速为2 m/s时，h=59.61 W/(m2·℃)；当风速为3 m/s时，h=88.93 W/(m2·℃)；当风速为4 m/s时，h=132.67 W/(m2·℃)。根据工程基本资料围岩参数为表2。

3.3 计算结果分析

3.3.1 通风温度对围岩温度场的模拟结果分析 运用有限元软件模拟，风速2 m/s不变，初始风温为4℃，得出距离进口10 m处通风3、30、60、90、120、150 d的围岩径向温度云图，如图3所示。

表2 围岩参数表

图3 隧洞不同通风天数距离进口10 m处围岩径向温度云图

通过作图软件提取图3中的数据作出径向围岩温度变化曲线图，如图4所示。

图4 隧洞不同通风天数距离进口10 m处径向围岩温度变化曲线

从图4中可以看出，隧洞通风3 d到30 d平均气温为-5.91℃，洞壁处的围岩温度降低10.28℃；通风30 d到60 d平均气温为-9.62℃，洞壁处的围岩温度降低2.26℃；通风60 d到90 d平均气温为-16.66℃，洞壁处的围岩温度降低3.09℃；通风90 d到120 d平均气温为-16.22℃，洞壁处的围岩温度降低1.36℃；通风120 d到150 d平均气温为-9.09℃，洞壁处的围岩温度升高0.58℃。从以上数据可以得知，通风温度降低则洞壁围岩温度也降低，随着通风时间的增加，通风温度对洞壁围岩温度的影响幅度逐渐减小。对比工程监测温度数据可知，模拟得出围岩的温度变化与监测围岩的温度变化一致。

从图4中还可以看出，通风150 d围岩在径向0m处温度降低16.41℃，变化幅度为318.0%;在径向1m处温度降低14.08℃，变化幅度为181.93%；在径向2m处温度降低10.82℃，变化幅度为122.00%；在径向3 m处温度降低7.13℃，变化幅度为79.34%。以上数据表明，通风150 d随径向距离的增加，空气对径向围岩温度的影响逐渐减弱。在径向0～2 m温度变化幅度超过100%，说明径向围岩在这个范围内受空气对流换热影响比较明显。径向围岩在10m左右时，围岩温度稳定在9℃(也就是围岩的初始温度)，且随着通风时间的增加，通风温度对径向围岩温度的影响幅度逐渐减弱。

运用有限元软件模拟，风速2 m/s不变，初始风温4℃，距离进口10、40、400、990 m处洞壁围岩通风3、30、60、90、120、150 d的围岩温度作出与进口不同距离的温度变化曲线图如图5、6所示。

从图5和6中可以看出通风从3 d增加到150 d，洞壁温度变化明显，随着通风时间的增加，通风温度对洞壁的温度影响逐渐减弱，120 d后气温还略有上升，这是因为3月份气温有所上升所致。从图5中可以看出，距离进口10m处比距离进口990m处的温度低1℃左右，隧洞中间部位温度明显高于两端洞口温度，变化最大时相差2.27℃，这与工程监测结果比较吻合。

从图6中可以看出，在通风30～120 d时，隧洞顶部的温度略高于隧洞底部的温度，0℃以下的温度天数长达135 d左右，洞壁最低温度达到-12℃左右，此结果与工程监测温度在0℃以下的天数和洞壁最低温度基本一致。

3.3.2 通风风速对围岩温度场的模拟结果分析 运用有限元软件模拟风速为1、2、3、4 m/s、初始风温4℃时，得出距离进口40 m内围岩的温度云图,如图7所示。

理解数学、理解学生、理解教学的水平是教师专业水平和育人能力的集中体现，是提高数学教学质量和效益的决定性因素，也是有效地提升学生数学核心素养的关键.当前的问题，首先是有些教师在“理解数学”上不到位导致教学偏差，机械解题训练成为课堂主旋律，而大量题目又不能反映数学内容和思维的本质，使数学学习越来越枯燥、无趣、艰涩，大量学生的感受是“数学不好玩”.

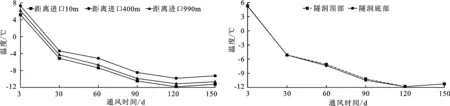
图5 隧洞距洞口10、400、990 m处温度随通风天数的变化曲线 图6 隧洞顶部与底部在距进口40 m处温度随通风天数的变化曲线

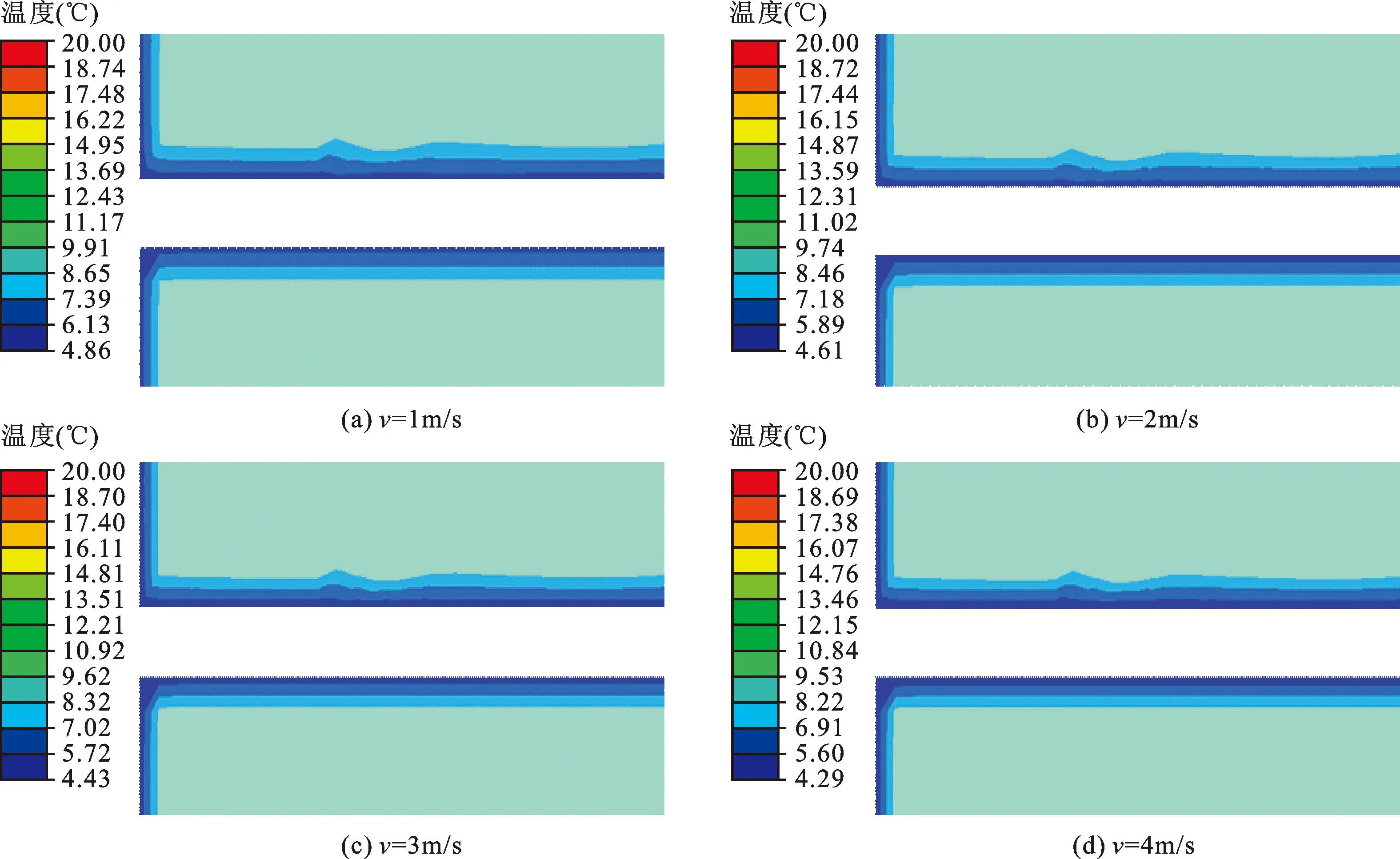
图7 不同通风风速隧洞距进口40 m内围岩径向温度云图

通过作图软件提取图7中的温度数据作出不同风速时的围岩温度变化曲线图，如图8所示。

图8 不同通风风速隧洞距进口40 m内洞壁温度变化曲线

从图8中可以看出，距离进口40 m内洞壁温度受风速影响变化比较明显，随着与洞口距离的增加，风速对洞壁温度的影响逐渐减小。通风风速为1、2、3、4 m/s时，隧洞距进口10 m处洞壁温度分别变化0.61、0.49、0.37、0.27℃，变化幅度分别为12.27%、10.37%、8.28%、6.28%。从以上数据可以得知，风速从1 m/s增加到4 m/s，空气与围岩的换热也随之增加，洞壁温度逐渐降低，但是随风速的增加，洞壁温度的变化幅度在减小。

运用有限元软件模拟风速为1、2、3、4 m/s、初始风温4℃时，得出距离进口10 m处围岩径向的温度云图，如图9所示。

通过作图软件提取图9中的温度数据作出不同通风风速围岩径向温度变化曲线图，如图10所示。

由图10中可以看出，风速从1 m/s增加到4 m/s，空气与围岩的对流换热增强，围岩温度逐渐降低。洞壁处围岩温度降低0.96℃，下降幅度为17.21%；径向0.5 m处围岩温度降低0.64℃，下降幅度为9.46%；径向1.0m处围岩温度下降0.31℃，下降幅度为3.99%。以上数据说明,径向围岩温度随风速增加而减小，温度变化幅度随径向距离增加而减小。

图9 不同通风风速隧洞内距离进口10 m处围岩径向温度云图

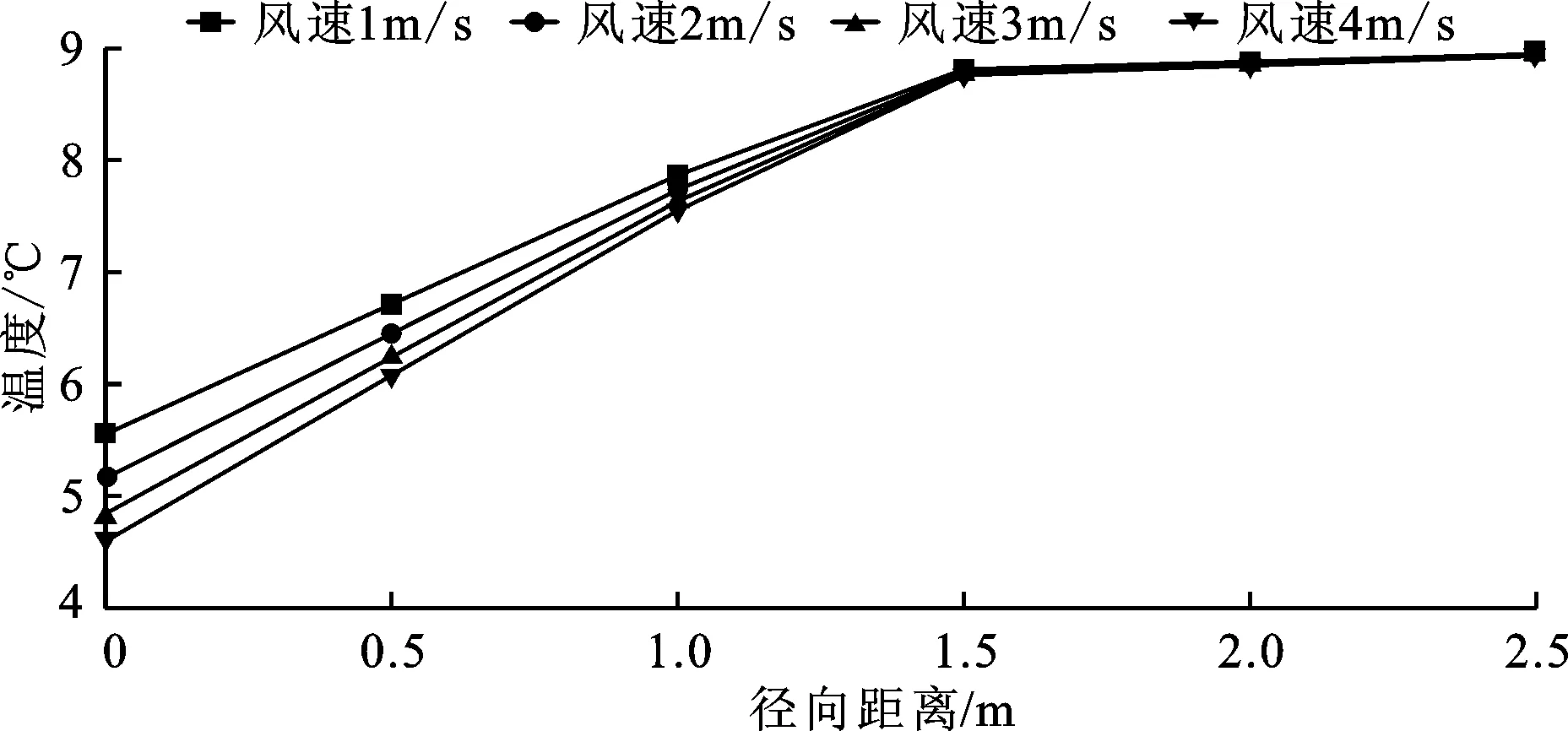
图10 不同通风风速隧洞内距进口10m处围岩径向温度变化曲线

4 结 论

(1)隧洞通风温度对轴向围岩和径向围岩的温度均有明显的影响，并且随着通风时间的增加，通风温度对围岩的影响幅度逐渐减小。对比工程监测温度数据可知，模拟得出围岩的温度变化曲线与监测围岩的温度变化一致。通风150 d隧洞围岩在径向0～2 m温度变化幅度超过100%，径向围岩在这个范围内温度变化最大。径向围岩在10 m左右时温度稳定在9℃(围岩的初始温度)，即通风150 d影响径向围岩在10 m以内。

(2)隧洞通风150 d，隧洞进口10 m处比距离进口990 m处的温度低1℃左右，隧洞中间温度明显高于两端洞口温度，变化最大时相差2.27℃，隧洞顶部温度略高于隧洞底部的温度，这与工程监测温度的变化趋势相吻合。0℃以下的天数长达135 d左右，洞壁最低温度达到-12℃左右，此结果与工程监测温度在0℃以下的天数和洞壁最低温度基本一致。

(3)通风风速从1 m/s增加到4 m/s时空气与围岩的对流换热也随之增强，围岩温度逐渐下降，随着风速的增加，围岩温度的变化幅度在减小。距离洞口40 m内洞壁温度随风速变化明显，距离洞口越远风速对洞壁温度的影响越小，围岩径向距离越小风速对围岩温度的影响越大。