水资源承载力的灰色模糊可变决策模型及应用
柴乃杰, 贾鼎元, 曾小雪
(1.贺州学院 建筑工程学院, 广西 贺州 542800; 2.中铁工程设计咨询集团有限公司, 北京 100055)
1 研究背景
水资源承载能力受到自然及人为等各种综合因素影响,而这些因素大多具有不确定性、模糊性以及相互关联性等特点[1]。因此,水资源承载力评价属于多指标复杂决策问题。国内外学者针对该复杂的综合评价与决策问题已进行了诸多研究,如戴明宏等[2]运用多层次模糊综合评价法对喀斯特地区水资源承载力进行了研究;刘东等[3]采用集对分析法评价了三江平原井灌区地下水资源承载力;高红霞[4]运用灰色投影寻踪法实现对国内4大直辖市的水资源承载力评价;李燕等[5]采用主成分分析方法研究长江经济带水资源承载力;杨琳琳等[6]通过构建BP神经网络模型来分析了新疆水资源承载力等。以上这些方法虽各有优势,但也存在一定的不足之处以及自身特定适用条件的局限性。例如:模糊综合评价法是通过选取模糊隶属度函数来进行分析和解决难以精确化的复杂问题,但如果建立的隶属度函数不恰当,则可能会造成较大的误差;再比如,主成分分析法一般适应于具有多个非线性相关指标的评价与决策问题,但当所评价问题的指标较少时,则会严重影响评价结果的准确性与客观性。正因如此,本文根据水资源承载力系统的复杂性、模糊性等特点,应用灰色系统理论,在构建水资源承载力评价指标体系以及确定待评价对象的基础上,以实测的样本指标特征值为依据,采用灰色关联度来分析和判断两组数列间的关联程度,一方面可以克服传统评价方法主观随意性大的缺点,另一方面具有指标数据要求低且计算量小,便于广泛应用的优势,为水资源承载力分析提供一条直观、有效的解决思路。
在上述基础上再借助模糊集合论,建立灰色模糊可变决策模型,并应用于甘肃省水资源承载力的实例进行验证,不仅为甘肃省水资源合理开发利用提供科学的依据,也为其他局域水资源承载力综合评价提供一种切实可行的方法。
2 模型的建立
2.1 灰色模糊隶属度
基于灰色模糊可变理论[7],建立水资源承载力综合评价的灰色模糊隶属度,具体建模步骤如下;
步骤1:设有待评价的m个对象组成样本集,依据n个指标的特征值,构建待评价对象的特征值矩阵为:
(1)
步骤2:按已知优劣两个级别指标标准模式对评价对象进行识别,可将水资源承载力分为特征值越大越优(正向)、越小越优(逆向)两类。为便于比较和计算,需将指标特征值矩阵进行规范化处理。
(2)
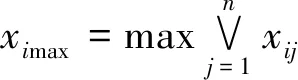
rij=
(3)
式中:分辨系数ρ取值为0~1,通常情况取0.5。
灰色关联系数的数学原理实质上与模糊理论中的隶属度具有一定的相似性[8],所以本文将运用灰色关联系数来计算拟研究对象i关于指标j相对于理想目标解的相对隶属度。灰色关联系数既能反映研究对象本身内部因素的影响,还能反映不同外部影响因素间的相互关联,进而确定其优属程度,即综合反映出关联系统的模糊性,最终得到由所有对象的灰色模糊隶属度所构成的判断矩阵R。
2.2 水资源承载力的灰色模糊可变决策模型
(1)根据上述灰色模糊隶属度,定义Tg=(1, 1, …, 1)、Tb=(0, 0, … , 0) 分别为优、劣目标的相对隶属度向量。设n个指标权向量为:
(4)
(2)对象i与优、劣目标的广义权距离分别为:
(5)
式中:wj为指标j的权重;rij为评价对象i关于指标j的相对隶属度;p为距离参数,p=1表示海明距离,p=2表示欧氏距离。
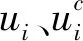
(4)为确定对象i与优、劣目标之间的加权广义权距离,可以借助上述相对隶属度,将其定义为权重,则有:
(6)
然后,求解对象i相对隶属度的最优值,建立目标函数为:
令dF(ui)/dui=0,得到水资源承载力的灰色模糊可变决策模型:
ui=1/[1+(dig/dib)α]
(7)
式中:α为优化准则参数。α=1表示模型选用加权最小一乘方准则;而α=2表示选用最小二乘方优化准则。
模型式(7)的几何、物理意义[9]为:当dig
通常,模型式(7)中α、p有以下4种组合形式[10],即①α=1,p=1;②α=1,p=2;③α=2,p=1;④α=2,p=2。
①当α=1,p=1时,模型式(7)变为:
(8)
公式(8)可视作为模糊综合评判模型,表示一个线性模型。
②当α=1,p=2时,模型式(7)变为:
ui=dib/(dig+dib)
(9)
公式(9)相当于理想点决策模型。
③当α=2,p=1时,模型式(7)变为:
ui=1/{1+[(1-dib)/dib]2}
(10)
公式(10)函数形态是关于djb单调增加的“S”型,所以可视作为Sigmoid型即S型函数。
④当α=2,p=2时,模型式(7)变为:
ui=1/[1+(dig/dib)2]
(11)
公式(11)称为模糊优选模型。
然后,运用公式(8)~(11) 4个可变决策模型分别计算各研究对象的相对隶属度向量,并将它们的平均值作为对象的综合相对优属度向量u。
最后,根据相对隶属度平均值u大小对各评价对象的水资源承载力进行排序,并按相对优属度平均值u越大,水资源承载力越小的原则,分析局域水资源承载力状况。
3 水资源承载力评价指标体系
3.1 评价指标体系建立
本研究参考王建华等[11]关于水资源承载力理论基础探析,以及国内在此方面的研究成果,并结合近年内甘肃省水资源状况,将影响其承载力指标体系划分为4大基本子系统。
(1)社会子系统。指整个水系统为人类提供了生活资源和能源。本研究中选取省内总人口、城市人口比重、生活用水量3个因子作为社会子系统的指标参数。
(2)经济子系统。指水资源系统对整个经济发展起着至关重要的物质循环作用。在本研究中,经济子系统选取5个因子,主要包括地区总产值、固定资产投资等。
(3)生态子系统。指水系统为维持水环境生态平衡提供保障。选取生态用水量、有效灌溉面积和废水排放量3个因子作为生态子系统的指标参数。
(4)水资源子系统。指的是水系统具有自身最大荷载量的限制。本研究中,水资源子系统选取水资源总量、总供水量和人均水资源量3个因子作为评价指标。
总之,影响水资源承载力的因素较多,本文结合甘肃省水资源实际状况,通过查阅相关统计年鉴,以及访问与征集专家意见,最终筛选和确定出一系列评价指标,建立水资源承载力评价指标体系。该体系主要分为目标层和指标层,目标层1为总体水资源承载能力,目标层2为4大类基本子系统,指标层为基本子系统所包含的各个具体指标,如表1所示。
3.2 指标权重系数的确定
综合评价中,赋权方法很多,而各种单一赋权方法在体现自身优点的同时,也不可避免地会暴露出某些缺陷。如熵权系数法[12],它可以通过数据本身的效用值,有效减少主观性的优势,但当数据间差异性较小时,该方法可能会产生较大误差,甚至得到荒谬的结论。为此,本文在选用熵权确定指标权重的基础上,将引入最大离差的方法[13]进行其缺陷的弥补,最大离差法旨在通过各属性值的区分度与离散性,来反映各指标属性对分类的相对重要程度,即当所有指标属性对全部类别的总离差达到最大时,得到最优权重。然后,再运用博弈论法集成两种赋权结果,确定出指标综合权重,使之更加符合目标的实际状况,以避免产生荒谬的结论。
3.2.1 熵权系数法的指标权重 熵权系数法是借助评价对象的指标特征值, 来判断各指标相对重要程度,具体步骤如下:
(12)
其中:
(13)
(2)计算指标j的熵权σj:
(14)
3.2.2 最大离差法的指标权重 在加权向量ω的作用下,构造的加权规范化决策矩阵为R*,则:
(15)
根据所有特征对所有类别的总离差极大化原理,同时满足单位化约束条件,应当调整ωj(j=1,2,…,n)降低ω={ω1,ω2,…,ωn}的不确定性,建立优化模型,则有:
(16)
(j=1,2,…,n)
由公式(16)线性规划模型,借助运筹学LINGO软件,可得到初步指标权重序列ω。然后,令所有属性对所有类别的总离差为D(ω),则有:
(17)
(18)
故该法得到的第j个属性的归一化权重为:
(19)

(20)
可转化为下面的线性方程组:
(21)

(22)
由以上博弈论方法可将指标熵权与最大离差法的指标权重进行集成,得到指标j综合权重:
(23)
4 工程实例分析
4.1 研究区概况及数据来源
甘肃省地处我国西北黄土高原地带,国土面积42.58×104km2,位居全国第7位。省内大部分地区干旱少雨,生态环境脆弱,主要有3大流域,包括内陆河流域、黄河流域和长江流域,各流域的年流量分别为62.31×108m3、66.13×108m3和63.11×108m3。甘肃省水资源以地表水资源为主,地表水资源多年平均值为282.11×108m3,约占省内总水资源量的97.48%,其中单位耕地面积平均水资源量5 670 m3/hm2,仅为全国平均水平的1/4。全省常年以来降水量为36.6~734.9 mm,多年平均蒸发量为1 100~3 000 mm。人均水资源量为843.722 m3,低于国际水资源紧缺的最低人均标准,属于严重缺水地区。
基于此,本文选择对该局域的水资源承载力进行研究。首先,通过分析全国及甘肃省水资源整体供需状况以及参考文献[15]中关于水资源承载力的评价指标,构建出甘肃省水资源承载力评价指标体系;然后,借助熵权法、最大离差法以及博弈论方法确定指标综合权值;最后,建立水资源承载力的灰色模糊可变决策模型,对甘肃省2006-2015年的水资源承载力进行动态分析与综合评价。本研究的数据资料全部整理于水资源相关统计资料,其中包括《中国统计年鉴》《甘肃统计年鉴》《甘肃经济统计年鉴》《甘肃省发展年鉴》《甘肃省水资源公报》和《甘肃省环境状况公报》等,初始指标数据如表2所示。
4.2 计算评价指标综合权值
在对上述甘肃省2006-2015年的所有评价指标数据进行有效调查统计和整理的基础上,运用组合赋权方法确定出指标的综合权重,具体综合权值计算与判断步骤如下:


(3)计算综合权重。利用博弈论集结函数分别将由熵值法计算得到的主观权重向量σ与由最大离差法确定的客观权重向量δ代入公式(20)及 (21),即可确定出主、客观权重的最优偏好系数α1=0.4342,α2=0.5658,进而得出指标的综合权值。
综上所述,将熵值法、最大离差法及基于博弈论的组合赋权法计算所得的权重列于表3。

表1 甘肃省水资源承载力综合评价指标体系
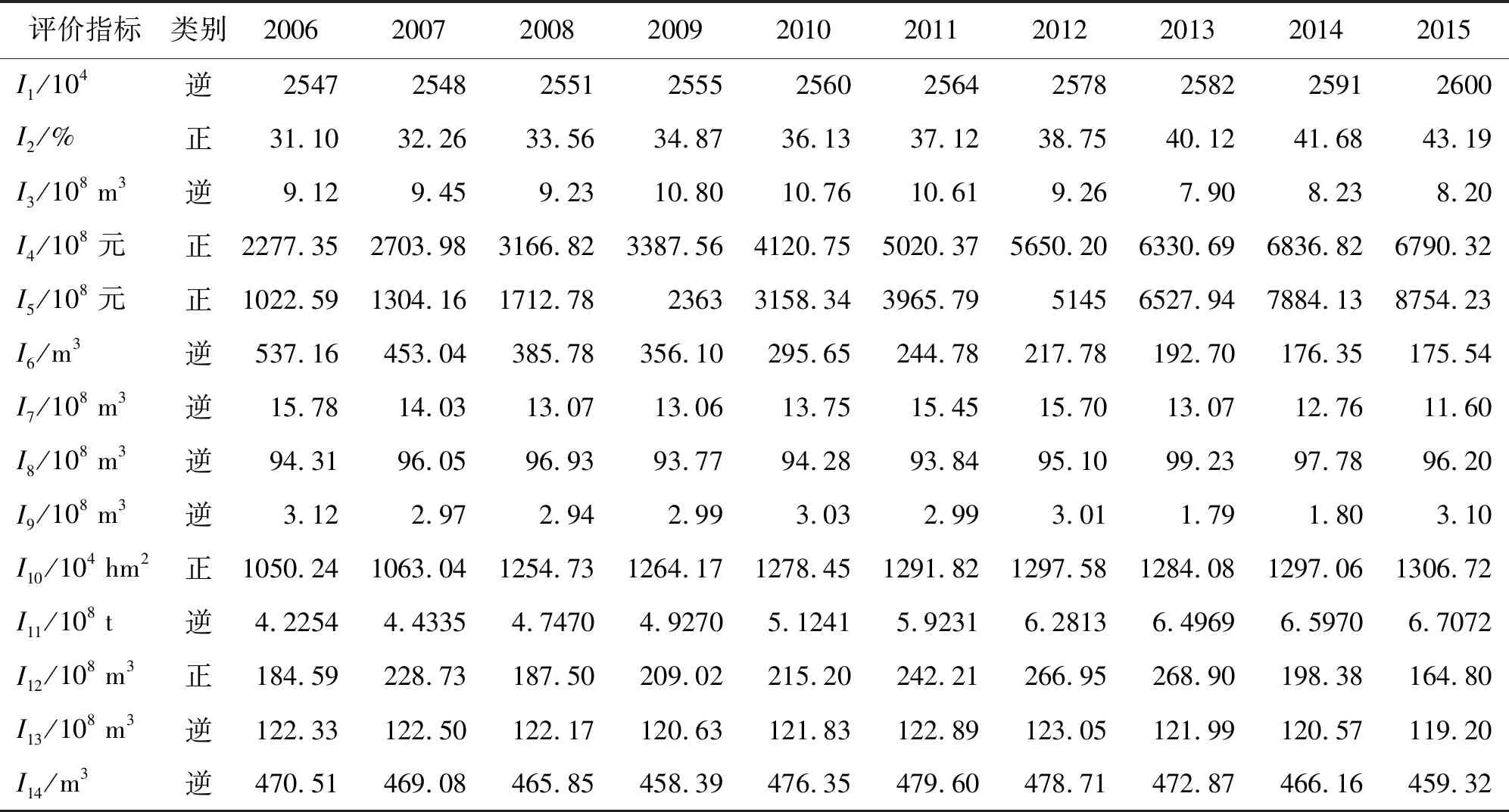
表2 2006-2015年甘肃省水资源承载力各评价指标初始数据
4.3 确定指标相对隶属度的平均值
首先,由表2构建出甘肃省水资源承载力评价指标特征值矩阵,其次运用公式(1)和 (2)对指标特征值矩阵作规范化处理,并利用公式(3)确定各个评价指标的灰色模糊隶属度,由此构成被研究对象的灰色模糊相对隶属度矩阵R。
然后,基于模糊可变集理论的模型式(7),分别计算判断矩阵R在参数α、p的4种不同组合下的级别特征值,即模型公式(8)~(11),进而可以得出甘肃省2006-2015年的水资源承载力在各年份所对应的相对隶属度平均值,结果见表4。
最后,依据各年份所对应的相对隶属度平均值大小,对甘肃省2006-2015年的水资源承载力状况进行排序。同时,相对隶属度平均值越大,说明水资源承载力越小,开发利用潜力越小,反之水资源承载力越大,开发利用潜力越大。为验证水资源承载力的模糊可变决策模型的合理性,将其排序结果与曹丽娟等[15]所建立的主成分分析方法进行对比,发现两种方法的评价结果吻合性良好,验证了本文所提模型的科学合理性与可靠性。
为了便于对2006-2015年甘肃省水资源承载力趋势进行分析,将其各年份所对应的相对隶属度平均值绘制成图1。
由图1可以明显地看出,水资源承载力相对隶属度平均值呈现出每年递增的情形,正说明甘肃省水资源承载力呈逐年递减的趋势。
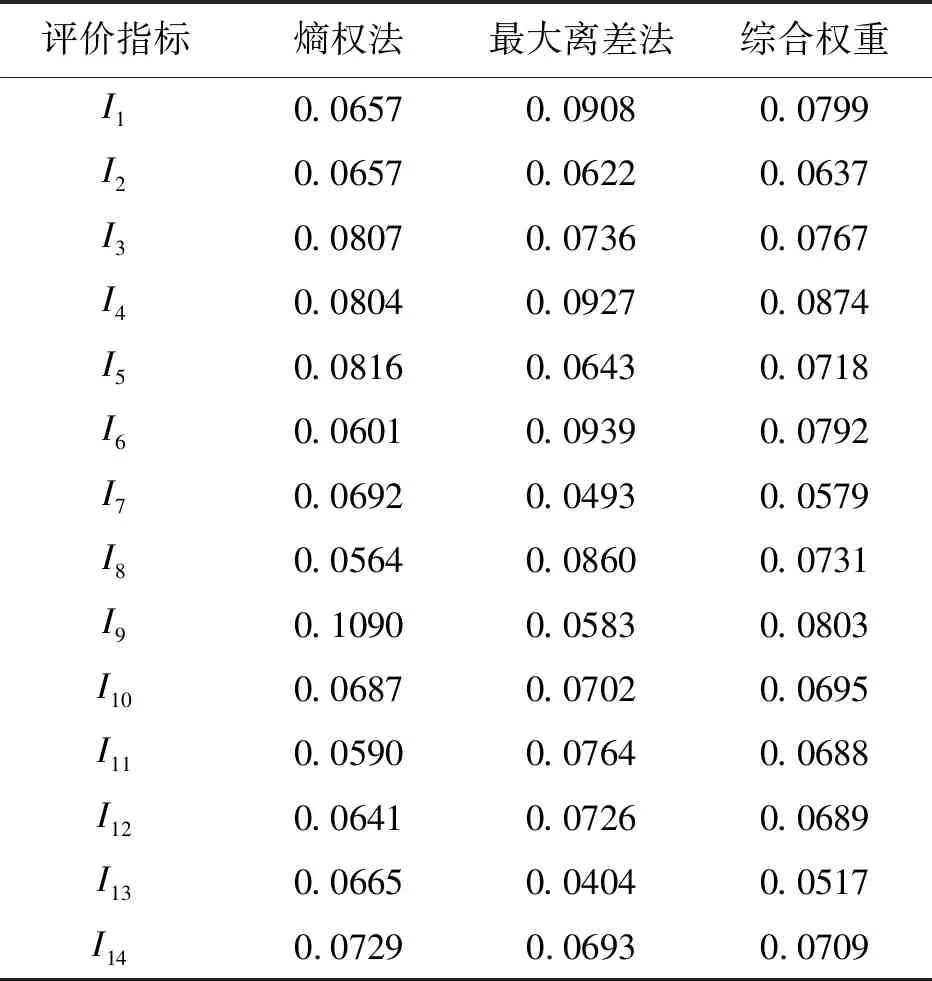
表3 各评价指标不同方法计算所得权重

表4 2006-2015年甘肃省水资源承载力相对优属度及排序

图1 2006-2015年甘肃省水资源承载力相对隶属度变化
5 结 论
水资源承载力评价属于复杂的多指标综合评价问题。首先,通过对水资源承载力水平的分析,确定出影响水资源承载力的子系统,主要包括社会子系统、经济子系统、生态子系统和水资源子系统。其次,为了进一步研究各子系统中所涉及指标对水资源承载力影响的相对重要程度,在采用熵权系数法和最大离差法的基础上,引入博弈论集成赋权的方法,计算各指标的综合权值。最后,建立灰色模糊可变决策模型,以甘肃省水资源承载力为实例,进行水资源承载力综合评价,并将灰色模糊可变决策模型的评价结果与已有文献中的主成分分析法作对比,发现两种方法的研究结论基本一致,即2006-2015年甘肃省水资源承载力呈逐年下降态势,从而验证了本文模型的可行性与合理性。根据本文研究结论得出,随着时间的推移,甘肃省区域水资源开发程度愈来愈低,水资源供需矛盾愈发突出。在研究时段内,2007年相对隶属度平均值最小,为0.4947,说明水资源承载力最大;而2015年相对承载力平均值达0.7787,说明水资源承载力最小。该结论为决策者制定出有效的缓解或补救措施提供了有力的参考依据。

