基于粒子群优化算法优化陷波器参数的永磁同步电机振动抑制技术方法研究

马金洋，张玉光，李国银，李 浪

(1.中车青岛四方车辆研究所有限公司,山东 青岛 266112；2.重庆中车四方所科技有限公司，重庆401133)

0 引 言

永磁系统能够准确跟踪或复现输入指令，凭借其良好的动态响应性能、高的准确性和稳定性，在各行各业中得到了广泛应用[1]。在中小容量高精度传动领域，广泛采用永磁同步伺服电机，以在转子上加永磁体的方法来产生磁场。由于永磁材料的固有特性，它不再需要外加能量就能在其周围空间建立很强的永久磁场。这既可简化电机结构，又可节约能量。目前市场上大部分全数字交流永磁同步电机伺服控制系统的产品大部分来自日本、德国和美国。近年来国内交流永磁同步电机伺服控制系统的研究非常活跃，天津大学、华中科技大学、沈阳工业大学等研究出由单片机构成的全数字交流永磁同步电机伺服控制系统，采用预测控制和空间矢量控制技术，改善了电流控制性能和系统响应精度。数字控制技术的应用，不仅使系统获得高精度、高可靠性，还为新型控制理论和方法的应用提供了基础。中国国内品牌主要有森创、华中数控、广州数控、南京埃斯顿和兰州数控等。

随着机电一体化步伐的不断加快，伺服系统已经渗透到许多领域，如数控、制造、航天等，这些领域是一个国家综合国力的重要体现方面。在伺服系统中，伺服电机与被驱动负载之间通常采用耦合的方式连接，由于伺服电机与被驱动负载之间的连接轴刚度较低，容易引起机械振动，而机械振动会影响伺服的控制精度[2-3]，因此，对伺服系统进行振动抑制显然显得十分重要。随着对永磁系统机械谐振研究的不断深入，在谐振频率检测方面也取得了较大进展。根据谐波检测的发展历程，已经存在了几种检测方法[4-5]：基于模拟滤波器进行谐波检测；基于傅里叶变换的谐波测量方法[6-8]；基于小波变换方法的谐波测量[9]；基于神经网络的检测方法[10]。为抑制检测到的谐振频率，文献[11]采用数字陷波滤波器来抑制机械谐振，但是这种陷波器的在中心频率点的陷波幅值很大，会对系统性能造成较大影响，此外陷波幅值和宽度由同一参数控制，不容易调节。文献[12]在传统的陷波器的基础上，经过扩展提出了一种改进的陷波器。陷波滤波器(notch filter)是一种可以在某一个频率点迅速衰减输入信号，以达到阻碍此频率信号通过的滤波效果。为有效解决伺服系统中由于机械刚度低产生的机械共振，本文以数字陷波器为抑制机械振动的基础，利用MATLAB对伺服驱动模型进行仿真，然后借助FDATool设计了2阶直接II型陷波器，消除了伺服和负载组成的双惯性系统之间的共振频率。

粒子群优化(Particle Swarm Optimization,PSO)是受鸟群迁徙的社会行为启发，基于群体智能的计算技术。PSO中的每个解(鸟群中每只鸟)被认为是“粒子”，其作用与遗传算法的染色体类似。但PSO不同于遗传算法，并不根据“父代”生成新的“子代”。PSO模仿了鸟群飞翔时的通信行为:每只鸟在飞翔时与其他个体通信，以确定处于最好位置的个体，以依赖于当前位置的速度飞向该最好个体，并在新的位置上计算适应度，上述过程重复进行，直至达到目标为止。PSO中每只鸟都具备学习自身经验(局部搜索)和其他群体经验(全局搜索)的能力。

针对共轴传动中的扭振问题，首先对其进行结构分析，建立数学模型，其次采用陷波器进行滤波。传统的陷波器设计对模型有一定的依赖性、参数调节较为复杂。针对参数不易整定存在的问题，提出一种基于粒子群算法的参数自整定方法。通过传函变换，实现了在线信号采集，在线优化处理，避免了在线优化容易激起系统振荡，优化过程无需建模、无振动、精确度高。

1 永磁电机控制振荡系统模型搭建

1.1 交流永磁电机数学模型

交流永磁同永磁电机的数学模型比直流电机要复杂的多，为了便于分析，在建立数学模型之前，做了如下假设：

(1)忽略磁滞损耗的影响；(2)不考虑铁心饱和；(3)不计涡流损耗；(4)转子上无阻尼绕组；(5)永磁材料的电导率为零。

交流永磁永磁电机在A-B-C坐标系上的电压方程可表示为

(1)

式中，ua、ub、uc为三相定子相电压的瞬时值，ia、ib、ic为三相定子相电压的瞬时值，Rs为定子电阻，ψa、ψb、ψc为定子相绕组磁链瞬时值。

以矩阵形式表示电压方程，可得：

(2)

式中，p为微分算子。ψf为永磁体磁链幅值，其在三相绕组中可以表示为

(3)

式中，ψra、ψrb、ψrc为转子相绕组磁链瞬时值，θ为永磁体磁链与定子绕组夹角。定子磁链方程可表示如下：

(4)

电磁转矩方程可表示为

(5)

式中，Te为电磁转矩，np为电机极对数。

1.2 双惯量末端振荡系统数学模型

双惯量系统又称为双质量系统，在工业应用中十分常见，如工业机器人、轧钢机等，一般由永磁电机、被驱动负载以及连接二者的传动轴等组成，双惯性系统模型如图1所示。

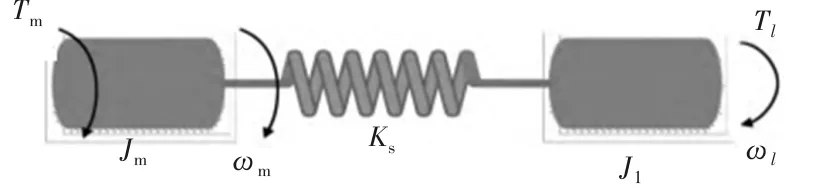
图1 双质量系统模型

图1中，JM、JL、Ks分别为永磁电机的惯性矩、负载端的惯性矩和传动轴的弹性系数、Tm、T1、ωm、ω1分别为电机转矩、扰动转矩、电机转速和负载转速。该系统的传递函数G(s)可以表示为式(6)。

(6)

式中，Jall=JM+JL，ωp为共振频率，ωz为反共振频率，表达式如:

(7)

(8)

从公式可看出，双惯性系统的共振频率和反共振频率是由电机和负载端的转动惯量以及轴的刚度产生。当负载端转动惯量很大时共振频率约等于反共振频率，当电机和负载转动惯量固定时，系统共振频率只与轴的刚度有关，轴刚度可表示为

(9)

式中，ro为轴半径，G为剪切模量，L为轴的长度。

根据图1可知，双惯性系统的状态方程可表示为

(10)

式中，Ts为连接永磁电机与被驱动负载的轴的转矩，BL、BM为负载和电机的粘滞系数。

2 粒子群优化算法基本过程

粒子群算法(PSO)的基本概念源于对鸟群觅食行为的研究。用一种粒子来模拟上述的鸟类个体，每个粒子可视为N维搜索空间中的一个搜索个体，粒子的当前位置即为对应优化问题的一个候选解，粒子的飞行过程即为该个体的搜索过程．粒子的飞行速度可根据粒子历史最优位置和种群历史最优位置进行动态调整．粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子单独搜寻的最优解叫做个体极值，粒子群中最优的个体极值作为当前全局最优解。不断迭代，更新速度和位置。最终得到满足终止条件的最优解。

算法流程如下：

1.初始化

首先，我们设置最大迭代次数，目标函数的自变量个数，粒子的最大速度，位置信息为整个搜索空间，我们在速度区间和搜索空间上随机初始化速度和位置，设置粒子群规模为M，每个粒子随机初始化一个飞翔速度。

2.个体极值与全局最优解

定义适应度函数，个体极值为每个粒子找到的最优解，从这些最优解找到一个全局值，叫做本次全局最优解。与历史全局最优比较，进行更新。

3. 更新速度和位置

4. 终止条件

(1)达到设定迭代次数；(2)代数之间的差值满足最小界限。

以上过程是PSO算法流程，PSO算法在优化过程中，种群的多样性和算法的收敛速度之间始终存在着矛盾．对标准PSO算法的改进，无论是参数的选取、小生境技术的采用或是其他技术与PSO的融合，其目的都是希望在加强算法局部搜索能力的同时，保持种群的多样性，防止算法在快速收敛的同时出现早熟收敛。

3 粒子群优化算法优化陷波器参数

3.1 陷波器设计

实际永磁系统大都是采用向控制系统中加入滤波器的方法来进行谐振补偿。陷波器可有效地滤除信号中谐振成分，陷波器的传递函数如：

(11)

式中，f为陷波中心频率，单位Hz；ξ为深度参数，表征了中心频率处幅频特性的深度，在中心频率处可提供-20lgξdB的幅值衰减；k为宽度参数，单位Hz，表示以陷波中心频率为中心幅值下降3 dB时的两侧宽度；通过调整滤波器的ξ，k两个参数，可以得到不同陷波幅值和带宽的频率特性，两个参数的整定原则为：

(1)当0<ξ<1时，且宽度参数k不变时，其频率特性曲线是凹陷的，且当ξ越小时陷波中心频率处提供的幅值衰减越大。

(2)当深度参数ξ固定不变时，随着宽度参数 值的增加，频率特性曲线凹口的范围逐渐大。

3.2 陷波器主要参数对陷波效果的影响探究

为了验证陷波器的正确性，模拟了一个幅度为1，频率为10 kHz的正弦波，其中掺杂着幅度为1，频率为20 kHz的正弦噪声，用Matlab设计一个20 kHz的陷波器，将掺杂了20 kHz噪音的10 kHz信号经过滤波器，利用FDATool导出Matlab程序验证陷波器的正确性并导出陷波器系数。发现仅改变apass参数由小变大，调节时间依次减小，但是对应的滤波范围变宽，“点”阻效果变差。由表2知，仅改变bw参数，带宽越大，虽然抑制越快，但窄带会变宽，即可滤频率增多，单一性差。研究证明了陷波器参数需要寻优，即参数apass和bw之间需要折中值以满足系统静动态响应。

3.3 PSO优化陷波器参数

本文所采用的技术方案是，一种利用PSO优化陷波器参数进行伺服共振抑制的方法，通过检测伺服系统的共振频率，采用PSO算法设计并优化陷波滤波器参数，达到抑制共振的目的，具体按以下步骤实施：

步骤1，初始化PSO算法及陷波滤波器相关参数、陷波器相关参数：采样频率f，陷波频率fnotch，带宽BW(0～10K)，品质因数Q、幅值衰减Apass；

步骤2，对需要进行抑制共振的伺服系统进行Matlab建模，通过程序FFT分析转速信号得到谐振点共振频率fnotch，检测伺服共振谐振点，然后，根据fs=10*fnotch和上述参数设计陷波滤波器；

步骤3，根据不同的谐振点和伺服系统对于滤波性能的要求，检测步骤2设计的陷波滤波器运用于伺服系统共振抑制是否满足静、动态性能指标，如不能满足性能指标，则通过PSO算法对陷波滤波器设计参数进行实时优化；

步骤4，根据优化结果设计陷波滤波器，并将其运用于相应的伺服系统中。

步骤2中采用PSO算法对陷波滤波器设计参数进行实时优化的目标为带宽BW，具体为：

(1)初始化整个粒子群体，即使得μ∈(0,1)；

(2)根据静、动态的性能指标参数，当μ在(0，1)之内，采用最小均方算法(LMS)，并将性能指标误差值作为粒子的适应度，得到基于PSO的陷波滤波器设计问题的评价函数为

(12)

式中，μ1和μ2分别为理想带宽和实际带宽；

(3)按照下式更新所有粒子的速度和位置。

Vi(t+1)=wVi(t)+c1r1(Pi-Xi)+c2r2(Pg-Xi)

Xi(t+1)=Xi(t)+Vi(t+1),-Vmin≤Vi≤Vmax

式中，Pi为第i个粒子达到的最好位置，Pg为所有粒子达到的最好位置，Vmax为粒子速度的最大变化，ri和r2为[0,1]范围内呈均匀分布的随机数。Vi(t+1)为估计的最优速度值、Vi(t)为当前的最优速度值、Xi(t+1)为估计的最优位置值、Xi(t)为当前的最优位置值、c1、c2为优化速度和位置的可调系数。

(4)不断优化确定r1、r2、c1、c2系数。

步骤4中陷波滤波器设计需满足以下规律：仅改变Apass参数由小变大，调节时间依次减小，但是对应的滤波范围变宽，“点”阻效果变差。

步骤4中陷波滤波器设计需满足以下规律。带宽越大，抑制越快，但窄带会变宽。

4 试验验证及分析

利用PSO优化陷波器参数进行伺服共振抑制的方法，具体按以下步骤实施。

步骤1，初始化参数：

PSO算法本身需要优化的参数不多，主要初始化陷波滤波器的相关参数。陷波器的陷波效果主要依赖以下参数：采样频率fs(0～100 kHz)，一般取值为10倍的陷波频率；陷波频率fnotch(0～10 kHz)，即FFT检测分析得到的共振频率；带宽BW(0～10 K)，通常是以-3 dB所对应的频带宽作为带宽的取值，另外也可以通过Apass参数的设计，确定在任意分贝的带宽；品质因数Q(0～10 K)，与BW和fnotch之间有固定关系，即fnotch=BW*Q，通带幅值衰减Apass(0～5)的默认值为-3 dB。

步骤 2，双惯性系统建模：

双惯性系统又称为双质量系统，由伺服电机、被驱动负载以及连接二者的传动轴等组成，双惯性系统模型如图1所示，图中，JM、JL、Ks分别为伺服电机的惯性矩、负载端的惯性矩和传动轴的弹性系数，Tm、T1、ωm、ω1分别为电机转矩、扰动转矩、电机转速和负载转速。该系统的传递函数G(s)可以表示：

(13)

式中，Jall=JM+JL，wp为共振频率，wz为反共振频率，s为微分算子。其中wp和wz的表达式如:

(14)

(15)

双惯性系统的共振频率和反共振频率是由于电机和负载端的转动惯量以及轴的刚度(即传动轴的弹性系数)产生。当负载端转动惯量很大时共振频率约等于反共振频率。当电机和负载的转动惯量都固定时，系统的共振频率只与传动轴的弹性系数有关：

(16)

式中，r0为轴半径，G为剪切模量，L为轴的长度。双惯性系统的状态方程如：

(17)

对双惯性系统进行Matlab建模，双惯性系统的三个组成部分分别是伺服电机、轴和负载。轴的输出对应于图1的T1，它的值决定于轴两端的速度差(ωm-ω1)，具体的扰动转矩公式为

(18)

式中，K为轴的刚度，单位是Nm，与Ks是同一变量，B是衰减系数，单位为Nm·s。建模成功后即可使双惯性系统表现出特定的振动频率，然后进行FFT检测即可。

步骤 3，根据不同的谐振点和伺服系统对于滤波性能的要求，通过PSO算法对陷波滤波器设计参数进行优化，主要优化的参数是带宽BW。

现有的基于矢量控制的永磁同步伺服电机共振抑制控制框图如图2所示，框图基于矢量控制，FFT分析及陷波滤波器设计模块在速度环与电流环之间，提取速度给定值与反馈值的误差中的谐波分量，然后通过PSO算法进行在线优化，如果满足伺服系统的静动态控制要求，确定陷波滤波器各项参数，否则不断检测谐波分量，不断优化，直到谐波被完全抑制。

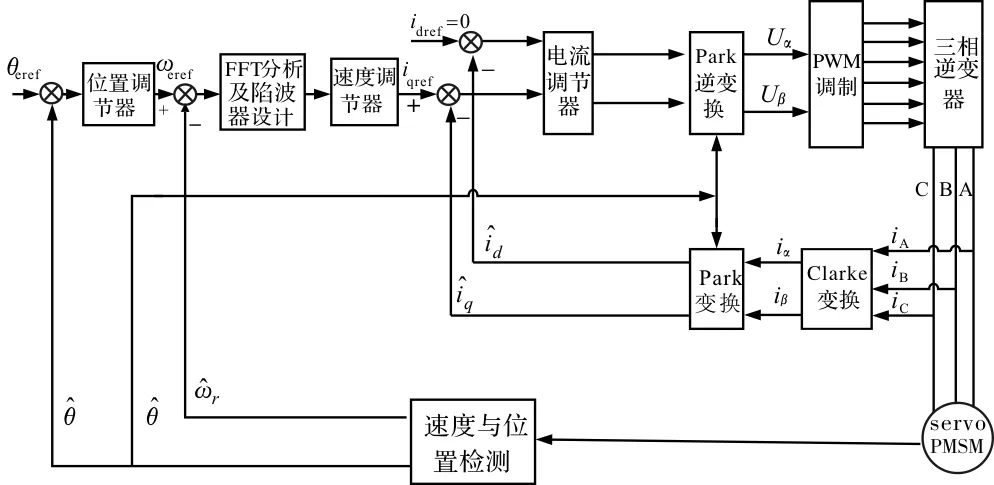
图2 基于矢量控制的永磁同步伺服电机共振抑制控制框图

由于带宽BW是影响陷波器设计的主要参数，而带宽与μ之间是一一对应的关系，即优化一个最好的μ是设计陷波滤波器的重点。

通常情况下，μ的取值范围是(0，1)，但其偏离最优解的大小和方向都是未知的，我们认为μ在(0，1)内是均匀分布的。

步骤3.1，根据静、动态的性能指标参数，当 在(0，1)之内，采用最小均方算法(LMS)，并将性能指标误差值作为粒子的适应度，所以，基于PSO的陷波滤波器设计问题的评价函数可以被描述如:

(19)

式中，μ1和μ2分别为理想带宽和实际带宽；z、z1、z2为z平面上的零极点。

步骤3.2，按照式(20)和式(21)更新所有粒子的速度和位置，

Vi(t+1)=wVi(t)+c1r1(Pi-Xi)+c2r2(Pg-Xi)

(20)

Xi(t+1)=Xi(t)+Vi(t+1)-Vmin≤Vi≤Vmax

(21)

式中，Pi为第i个粒子达到的最好位置，Pg为所有粒子达到的最好位置，Vmax为粒子速度的最大变化，r1和r2为[0,1]范围内呈均匀分布的随机数。Vi(t+1)为估计的最优速度值，Vi(t)为当前的最优速度值，Xi(t+1)为估计的最优位置值，Xi(t)为当前的最优位置值，c1、c2为优化速度和位置的可调系数。

步骤3.3，不断优化确定r1、r2、c1、c2系数。

步骤4，整体的自适应参数优化的流程图如图4所示，判断条件“是否最优”的标准是最终设计能够完全抑制谐波的陷波滤波器，满足系统的性能。

步骤5，设计陷波滤波器。

步骤5.1，通过程序FFT分析转速信号得到谐振点频率fnotch。

步骤5.2，根据步骤3计算采样频率fs=10*fnotch。

步骤5.3，假设数字多频陷波滤波器可以对M个不同频率陷波，则理想多频陷波系统的频率响应为

(22)

式中，ω(0≤ωi≤π)为数字频率。

整个过程的流程图如图3所示。

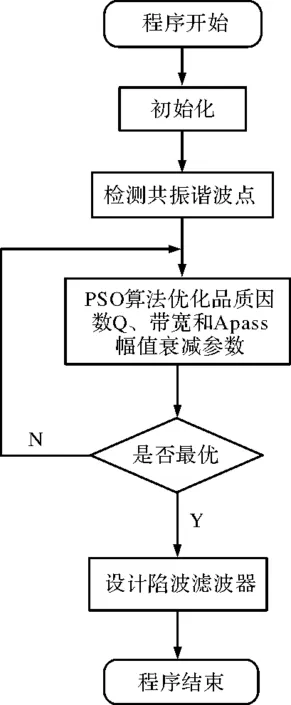
图3 优化过程流程图

(23)

(24)

式(23)中μ越小，极点越靠近单位圆，则频率响应曲线凹陷越深，凹陷的宽度也越窄，很明显这个传函对应的是个二阶系统。

步骤 5.4，根据二阶系统的传递函数可得出相应的ΔN、Trise、Tset、Ess、Δδ。例如伺服二阶系统对于共振抑制的静、动态性能指标如下。

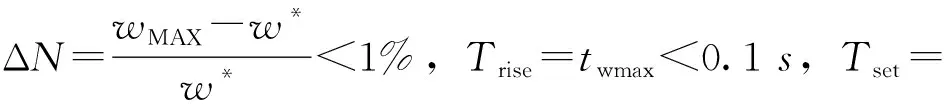
步骤 5.5，PSO参数优化过程分为五步：第一，确定PSO的优化目标参数为BW；第二，初始化整个粒子群体，即使得μ∈(0,1)；第三，确定PSO算法的适应度，基于步骤五中的各项指标确定评价函数；第四，所有例子的速度与方向更新；第五，判断是否满足步骤5.4中的各项条件。

步骤 5.6，根据步骤1中的BW初始值设计陷波滤波器并用于伺服系统的共振抑制中。当伺服电机运行时，结合步骤3.2和步骤3.3，实时优化陷波滤波器参数，设计满足静动态性能指标的滤波器。

发现仅改变Apass参数由小变大，调节时间依次减小，但是对应的滤波范围变宽，“点”阻效果变差。带宽越大，虽然抑制越快(带宽大响应快)，但窄带会变宽(即可滤频率增多，单一性不好)。