基于灰色关联分析的短期风速预测方法
李嘉宇,王东风,张 妍
(华北电力大学 控制与计算机工程学院,河北 保定 071003)
0 引言
近年来,风能作为一种清洁的可再生能源,引起了全世界的广泛关注,风力发电已成为最具发展前景的新能源发电方式之一。随着风力发电技术的发展,风速自身的随机性和间歇性对电网调度的影响越来越大。准确的风速预测结果可有效降低风电功率的不确定性,保障电网的经济、安全、稳定运行。
现有的风速预测方法主要分为物理方法和统计方法。物理方法是基于天气预报数据,考虑风场地形起伏程度等因素进行预测的方法[1]。物理方法无需大量的历史数据即可获得较高精度的预测结果,但建模和求解的过程复杂,通常被用于新建风电场的中长期风速预测。统计方法则利用历史数据进行建模,通过分析输入和输出的映射关系来获取预测结果[2]。相比于物理方法,虽然统计方法应用于中长期风速预测时的精度较低,但其在建立模型时无须考虑复杂的地形及气候条件,结构简单、容易建模。在现有的风速预测方法中,大部分方法集中于统计方法。统计方法还可进一步分为时间序列法[3]和人工智能法[4],这两种方法在短期风速预测中均得到了广泛的应用。文献[5]构建了卷积神经网络(Convolutional Neural Network,CNN)和双向门控循环单元(Bidirectional Gated Recurrent Unit,BGRU)结合的预测模型,其预测精度优于传统的预测模型。文献[6]提出了一种新型的混合预测模型,通过多目标优化算法对回声状态网络(Echo State Network,ESN)模型进行优化,保证了预测的稳定性和准确性,具有很大的应用潜力。文献[7]提出了一种基于长短期记忆网络(Long Short Term Memory,LSTM)的超短期风速预测模型,针对不同情况下的风速具有较好的适应性。现有研究在建立风速预测的统计模型时均未对所构建模型的输入变量进行详细研究。由于输入变量在类型上的差异会影响到风速预测的精度[8],并且针对大多数统计模型而言,如果将具有相似特征和变化趋势的数据作为变量输入,统计模型的训练难度将会明显降低[6]。
为此,提出一种基于灰色关联分析(Grey Relation Analysis,GRA)的短期风速预测方法。该方法以风速序列为基准,对采集到的气象数据进行灰色关联分析,并根据所得到的关联分析结果,选择构建LSTM 模型的输入变量进行训练,计算得出风速的预测结果。
1 理论基础
1.1 灰色关联分析
GRA 是一种多因素统计的算法,其基本思想是通过确定参考数据列和若干个比较数据列之间几何曲线的相似程度来判断其联系程度是否紧密。通过GRA,可分析系统中各因素间的联系,确定各因素之间相对关联性的强弱,其具体计算步骤如下:
1)确定分析数列。
确定反映系统行为特征的参考数列Y 及对应的比较数列矩阵X 为:
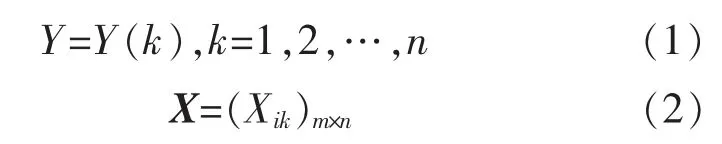
式中:Y(k)为数列Y在第k个时刻的值;n 为系统总采集点数;Xik为数列矩阵X 的第i 个特征在第k 个时刻的值。
2)变量无量纲化。
由于系统中各特征数列中数据的量纲通常是不同的,一般在计算关联度之前,先将步骤1)参考数列与比较数列矩阵X 中各元素进行无量纲化处理,得到无量纲的参考数列Y′与比较数列矩阵X′。

3)计算关联系数ξi,计算公式为:

式中:ξi(k)为对数列Y′(k)在第k 个时刻的关联系数;P 为分辨系数,通常情况下取0.5。
4)计算关联度ri。

1.2 长短期记忆网络
LSTM 模型是Hochreiter 和Schmidhuber 提出的一种时间周期网络,已在预测领域得到了广泛的应用。LSTM 有着类似递归神经网络(Recursive Neural Network,RNN)的链式结构,利用给定的输入和输出数据对模型进行训练,可以在有限样本的条件下得到风速预测的结果。LSTM 模型的结构如图1 所示。

图1 LSTM 结构
图1 中,最左侧的遗忘门用来查看模型的当前输入和当前输出,然后为单元格的每个数字输出0~1 的数字,其中1 表示完全保留,0 表示完全删除,具体公式为
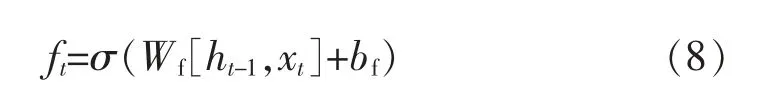
式中:ft为t 时刻模型通过遗忘门后所得到的输出;Wf、bf分别为遗忘门对应的权重和偏置;ht-1为上一个细胞的输出;xt为当前细胞的输入;σ 为通过将细胞的当前输入值xt收敛到[0,1],从而加强LSTM 网络对xt特征识别度的Sigmoid 函数,该函数的具体表达式为

随后需要决定有多少新的信息加入细胞中,这一部分的工作由输入门和状态单元来完成,具体公式为:

式中:it为t 时刻模型通过输入门后所得到的输出;Wg、bg分别为输入门对应的权重和偏置;为t 时刻需要更新的备选内容;Wc、bc分别为状态单元对应的权重和偏置。此时可通过式(12)来更新状态单元Ct的值,并通过输出门确定模型的最终输出ht。
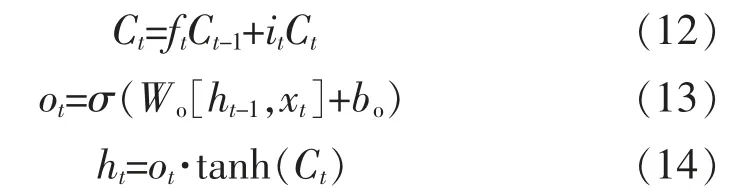
式中:ot为t 时刻模型通过输出门后所得到的输出;Wo、bo分别为输出门对应的权重和偏置。
2 GRA-LSTM 模型
LSTM 模型具有较强的非线性拟合能力,但针对风速预测而言,LSTM 模型不能完全分析出风速与其他气象影响因素之间的非线性和趋势相关性。此外,在可再生能源行业长期数据有限的情况下,需要合理选择模型的输入变量,以保证LSTM 模型的训练效果。
为此,构建GRA-LSTM 模型,该模型基于风速的历史数据以及GRA 算法确定最优输入变量,模型可具体描述为
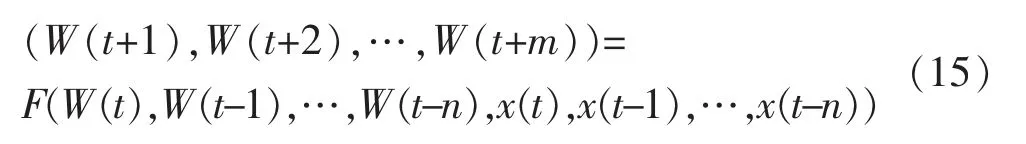
式中:W(t+1),W(t+2),…,W(t+m)分别为t+1,t+2,…,t+m 时刻的预测风速;W(t),W(t-1),…,W(t-n)为t 时刻及其前n 个时刻的风速序列;x(t),x(t-1),…,x(t-n)为t 时刻及其前n 个时刻通过GRA 模型确定的对风速影响较大的其他气象影响因素序列;F(x)为LSTM 模型。GRA-LSTM 详细流程如图2所示。
3 有效性验证
3.1 模型输入变量选择

图2 GRA-LSTM 方法流程
以美国能源部太阳能辐射研究实验室Golden站点2019 年1—3 月的实测数据为例,对算法的有效性进行验证。数据包含种风速、温度、压强、云层厚度、相对湿度、风向及露点7 种数值天气预报的信息,数据采样间隔为10 min。
为研究不同输入变量对风速预测模型预测结果的影响,选择风速序列作为基准序列,并对其他6 项气象影响因素进行灰色关联分析,所得到的结果如表1 所示。

表1 风速序列影响因子关联度
由表1 可以看出,影响因子与风速序列的关联程度从高到低依次为风向、相对湿度、温度、露点、压强和云层厚度。其中,风向和相对湿度的关联度明显高于其他气象因子,且两者的关联度数值十分相近,分别为0.649 和0.648。其他气象因子的关联度相比于风向和相对湿度二者有明显降低,且除云层厚度的关联度为0.367 外,其他气象因子之间的关联度相差较小。
此外,在样本数据有限的前提条件下,输入变量维度的增加会导致LSTM 模型的训练不够充分,进而降低最终的预测精度;而输入变量的维度过低又会导致模型对数据特征的提取不够充分而使预测结果出现欠拟合的状态。因此,在综合考虑上述因素和试验结果的条件下,选定风速、风向和相对湿度3 种因素为输入变量的LSTM 模型作为本文所提出算法的对应模型,用于验证其预测性能。
3.2 预测结果及误差分析
为了确保试验变量的唯一性,除所提出的算法模型之外,将气象因素两两组合并加上风速序列作为各LSTM 模型的输入变量,以确保所有模型输入变量的数量均为3。随后分别训练LSTM 模型,并与风速、风向和相对湿度作为输入变量的LSTM 模型的预测结果进行对比。选择2019-03-31 作为预测日,通过当日的实际风速与不同输入变量情况下模型的预测风速进行对比,以验证所提算法的有效性,预测的时间间隔为10 min。
在得到风速预测的结果后,常用均方根误差RMSE、误差平方和SSE来估计风速预测模型的性能,定义为:
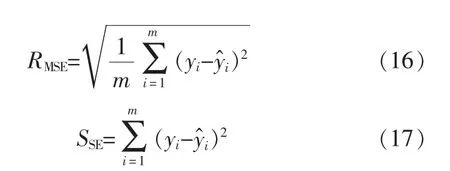
式中:yi为i 时刻风速实际值;为i 时刻风速预测值;m 为系统总采集点数。
其中,RMSE对数值较大的误差更为敏感,SSE则是不同风速序列预测点的绝对误差之和[9],通过这两种指标可综合评价模型的预测性能,各模型的试验结果如表2 和图3 所示。

表2 同风速下不同其他输入变量模型的误差指标值

图3 同风速下不同其他输入变量模型的误差曲线分布
由表2 和图3 可知,所提算法确定的输入变量所构建的模型两种误差指标RMSE和SSE均为最小值,分别为1.023 和150.698,并且在误差曲线图中每点的纵坐标更靠近0,说明该预测模型具有更小的误差和更高的预测精度,证明了本文所提出算法的有效性。
4 结语
在构建LSTM 模型时,输入变量类型的差异会影响到最终的预测结果。试验结果表明,以风速参考数据序列,对风向、相对湿度等气象因素进行灰色关联分析,可确定模型最优输入变量的类型,并有效提高模型的预测精度。
在试验数据充足且各气象因素的关联度相差不大时,难以确定作为模型输入变量的气象因素的数量,这是本文所提出方法的不足之处。
在之后的研究中,将基于此方法进行更加深入的研究,寻找同时确定模型最优输入变量的类型和数量的方法,以最大限度地提高风速预测的精度。

