爆炸荷载下钢筋混凝土结构数值分析

杜新权，李默阳

（中国船舶重工集团公司第七〇五研究所，陕西 西安710075）

0 引言

开展工程结构及装备的防爆性能实验研究，设计和建造多功能的爆炸实验装置，必然涉及建筑物的结构设计。目前，建筑物结构设计的研究主要侧重于约束验证、模型建立、承载力公式推导等方面。针对抗震性能、抗爆炸冲击性能等方面的研究明显不足，在结构设计的荷载数值、构建几何模型等方面，以构造数据为主，缺乏科学性、严谨性，制约了建筑物结构设计理论的发展和进步。本文提出的爆炸荷载下钢筋混凝土结构计算分析模型和数据结果，为建筑物结构的抗爆设计、防爆加固和结构选型提供了可靠的设计依据，对爆炸荷载作用下结构设计计算数据输入、几何模型选择具有参考价值，对相关军民用爆炸物品涉及建筑物结构设计规范的编制补充具有实际意义。

爆炸荷载的荷载峰值高、持续时间短，弹塑性较好的钢筋混凝土结构和其他结构形式相比较，具有显著优势。因此，研究钢筋混凝土结构在爆炸荷载作用下的动力响应具有重要的理论价值和实际应用价值。

钢筋混凝土结构柱通常被用做钢筋混凝土框架结构体系，填充墙对结构的影响较小，可以将其从整体结构中拿出来进行局部抗爆分析。本文利用有限元分析软件ANSYS /LS-DYNA，建立钢筋混凝土结构柱有限元模型，对钢筋混凝土结构柱动态响应进行研究。结果表明：钢筋混凝土结构具有良好的抗爆性能，模拟结果可为钢筋混凝土结构的抗爆设计、抗爆加固和结构选型提供依据。

1 理论依据

1.1 爆炸冲击峰值和最大弹性动位移

炸药爆炸过程持续时间较短，可将爆炸看作是一个瞬态过程。爆炸后生成的高温、高压爆轰产物会急剧膨胀，使周围气体位移，膨胀气体形成压缩空气层，即爆炸波。我们要了解爆炸波，就需要知道爆炸波过后介质的压力、密度、质点速等状态参数度以及爆炸波作用下的时间、冲量等。

爆炸波在无限大气中传播，爆炸波的压力和速度比较容易测量，特别是爆炸波的压力，经过大量的实验研究，得出了很多计算爆炸波超压的经验计算公式[1-2]。

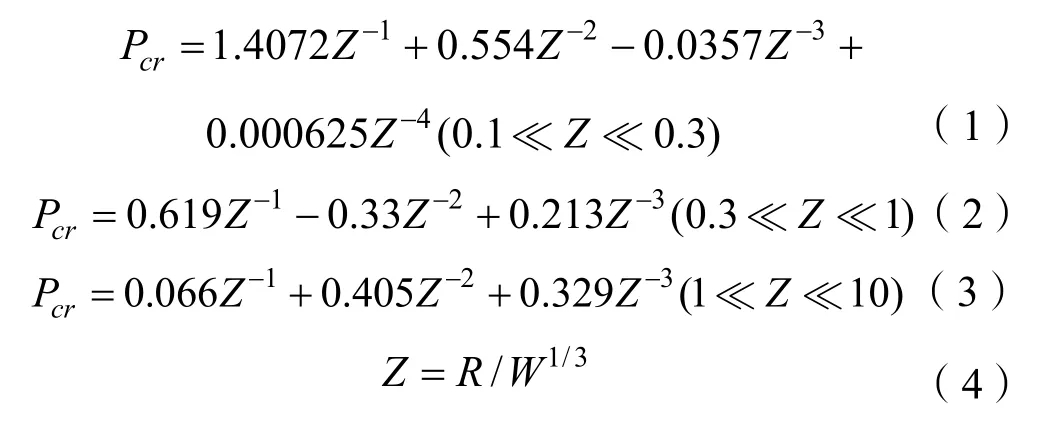
式中：Pcr为爆炸冲击峰值，MPa；Z为比例距离；R为测点与爆炸中心的距离，m；W为等效 TNT药量，kg。

基于能量守恒原理提出的等效单自由度方法对钢筋混凝土结构柱在爆炸荷载下的动力响应进行理论分析。首先，求解钢筋混凝土结构柱的组合刚度；其次，根据钢筋混凝土结构柱的受弯特点推导塑性极限弯矩；最后，将爆炸荷载简化成三角形荷载，利用等效单自由度方法求解钢筋混凝土结构柱在爆炸荷载作用下的最大动位移。

单自由度体系是简化瞬态问题的有效方法，如图 1所示。单自由度体系中，结构等效为一个质点，结构抗力等效为弹簧，质量为Me的结构，受到外力F（t）作用，结构抗力位移为y，弹簧刚度为Ke，t为持续时间，则该单自由度体系的运动方程为

图1 单自由度体系示意图Fig.1 Schematic diagram of single-degree freedom system

爆炸荷载可以简化为峰值为Fm，最大持续时间为td的下降三角形荷载，如图2所示。

图2 爆炸荷载简化示意图Fig.2 Simplified schematic diagram of explosion load

这时，爆炸荷载表达式为

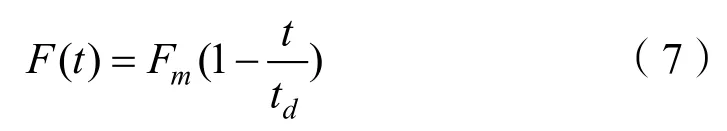
将式（7）带入式（5），得到无阻尼单自由度弹性体系的运动方程：

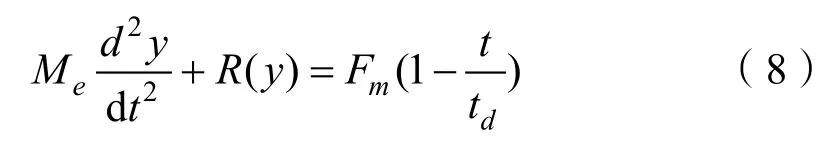
式（8）微分方程的通解为

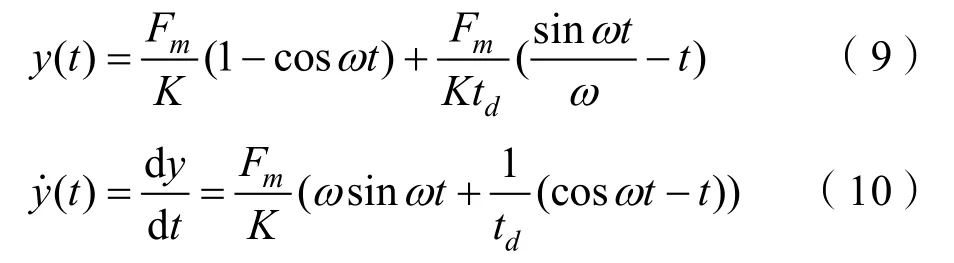
式中：ω为单自由度体系自振频率；y(t)和分别代表位移和速度。

爆炸荷载作用下结构的最大响应为结构最大弹性动位移ymax，令求得tmax时y(t)极值即为最大弹性动位移ymax。

工程应用中，通常采用图 3直接查出最大位移，以避免求解单自由度弹塑性体系繁琐的微分方程。

定义延性比μ为爆炸荷载作用下最大位移ymax与静力作用下位移y0之比：

图3 无阻尼单自由度体系在三角形脉冲荷载下的最大响应Fig.3 Maximum response of undamped single-degree freedom system under triangle pulse load

图3中：Ta表示动载持续时间；T0表示固有周期；Re表示等效单自由度体系的等效屈服抗力；Fe表示等效单自由度体系的等效外力。

1.2 ANSYS/LS-DYNA结构数值计算分析

有限元仿真软件ANSYS/LS-DYNA计算准确、应用广泛、材料模型和单元类型丰富，含有高度非线性瞬态动力分析模块，是著名的通用显示动力程序，在国防领域中的应用十分广泛。

ANSYS/LS-DYNA以LAGRANGE算法为主，兼有ALE和EULER算法，支持炸药、空白材料模型、高能炸药的状态方程和起爆设置。

LAGRANGE算法是目前研究高速碰撞应用最多的方法，可以跟踪固定质量单元的运动，计算网格固定材料内部，随材料变形。采用LAGRANGE法的控制方程简单、概念明确，可以方便描述碰撞过程中复杂的边界条件和定义接触面。

EULER算法中计算网格固定在空间，材料则在网格间运动，在研究高速碰撞时可以避免LAGRANGE程序由于变形大而产生的网格畸变问题。但是，EULER法计算复杂、不直观，因此，发展出了混合方法ALE，适用处理超高速碰撞问题。

ALE算法可以对炸药爆炸后冲击波的传播过程、爆炸冲击波作用下钢筋混凝土结构破坏过程进行数值模拟，把破坏特征以及爆炸冲击波的压力时程曲线与典型经验公式结果进行对比，进而评估模拟结果的正确性。

2 数值计算分析

2.1 建立模型

炸药、空气介质和钢筋混凝土模型均使用ALE单元类型，采用轴对称算法，对1/2模型施加约束来取代整个模型进行计算。数值模型中，采用尺寸为400 mm×400 mm×400 mm的立方体来模拟TNT炸药，炸药当量为200 kg，炸药中心与钢筋混凝土结构之间的距离为3 000 mm。钢筋混凝土结构高度3 000 mm，宽度400 mm，长度800 mm，钢材采用 Q345，混凝土的强度等级为 C40。如图 4-5所示，模型参数如表1所示。

钢筋混凝土结构采用LAGRANGE网格划分，在柱顶和柱底的节点上施加了3个方向上的位移约束，炸药和空气采用EULER网格划分，在各截面上施加无反射边界条件，钢筋混凝土结构和空气之间采用流固耦合算法。

在 ANSYS/LS-DYNA中，建立模型，输出计算中间数据文件“k文件”，对“k文件”进行修改，递交求解，最后，利用后处理软件 LS-PREPOST进行分析。

表1 模型参数Table 1 Parameters of numerical model

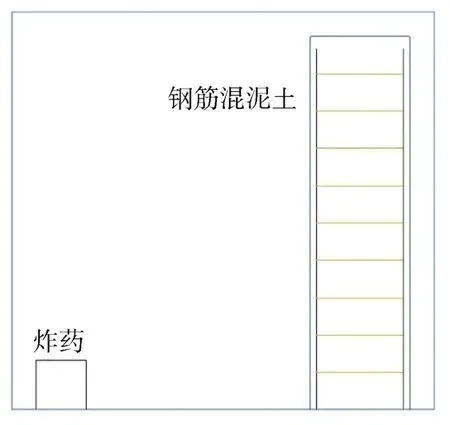
图4 数值几何模型Fig.4 Numerical Geometric model

2.2 施加荷载

图5 有限元网格划分示意图Fig.5 Partition schematic diagram of finite element meshing

计算模型涉及炸药、空气介质等材料，其中炸药材料选用高能炸药燃烧与增长模型 MAT_HIGH_EXPLOSIVE_BURN，炸药的状态方程模型选用高能炸药形式的EOS_JWL状态方程，空气介质选用空白材料模型 NULL，钢材选用 MAT_PLASTIC_KINEMATIC材料模型，混凝土采用MAT_JOHNSON_HOLMQUOSIT_CONCRETE材料模型，混凝土和钢材的材料参数如表 2-3所示[3-6]。

表2 混凝土MAT_JOHNSON_HOLMQUOSIT_CONCRETE材料模型参数Table 2 Parameters of MAT_JOHNSON_HOLMQUOSIT_CONCRETE concrete material model g-cm-μs

表3 钢材MAT_PLASTIC_KINEMATIC材料模型参数Table 3 Parameters of MAT_PLASTIC_KINEMATIC steel material model g-cm-μs

2.3 结果分析

1）利用LS-POST后处理器可方便得到典型装药空气中爆炸时，在t=0.2 ms，t=0.3 ms，t=0.5 ms时，有限元仿真模型压力云图如图6-8所示。

爆炸发生后，很快形成冲击波。t=0.2 ms时，冲击波波阵面清晰，爆心位置形成由内向外传播的稀疏波；t=0.3 ms时，冲击波压力在开口自由端迅速卸载，形成向下传播的稀疏波；t=0.5 ms时，开口自由端反射冲击波强度明显低于界面反射冲击波，波阵面也较为模糊；t=0.9 ms时，冲击波的强度逐渐降低。

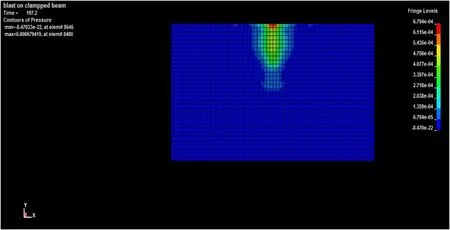
图6 有限元仿真模型压力云图（t=0.2 ms）Fig.6 Pressure nephogram of finite element simulation model （t=0.2 ms）

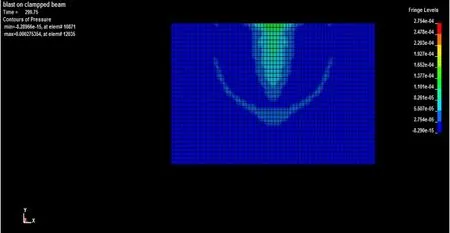
图7 有限元仿真模型压力云图（t=0.3 ms）Fig.7 Pressure nephogram of finite element simulation model （t=0.3 ms）

根据仿真模拟数值结果，等效 TNT当量200 kg，有限元仿真模型爆炸冲击波的峰值Pcr=4.75 MPa，根据公式（1）-（4）计算得出Pcr=4.67 MPa，数值模拟和理论计算结果相差1.7%，验证了数值模型的可信性。

2）在爆炸荷载作用下，钢筋混凝土结构柱塑性应变云图如图9所示。

钢筋混凝土结构柱在爆炸荷载作用下，整体破坏模式呈现为弯剪型破坏，在柱头、柱脚局部出现明显的塑性应变。由于爆炸爆心位于柱中部，柱中部塑性应变大于周边部分。

图9 有限元仿真模型塑性应变云图（t=0.7 ms）Fig.9 Plastic strain nephogram of finite element simulation model（t=0.7 ms）

3）在爆炸荷载作用下，钢筋混凝土结构柱跨中y方向最大位移时程曲线图，如图10。

图10 柱跨中y方向最大位移时程曲线图Fig.10 Time course curve of span column in maximal displacement along Y direction

爆炸发生后6.34 ms，柱子中部达到最大位移，位移最大值为25.05 mm。根据简化的等效单自由度体系方法计算的动力响应计算公式，最大位移为23.6 mm。由于爆炸冲击荷载的复杂性，在同一数量级上即可认为结果比较准确。本文中数值模拟和理论计算结果相差6%，验证了数值模型的可信性[7-11]。

4）混凝土强度等级的影响。

为研究混凝土强度等级对钢筋混凝土结构柱在爆炸荷载下动力性能的影响，对3种不同混凝土强度等级的构件模型进行对比分析，模型参数如表4所示。

表4 各工况的数值模型参数Table 4 Parameters of numerical models in each working condition

根据图11不同混凝土强度等级结构柱跨中的y方向最大位移时程曲线图，可以得出：混凝土的强度等级Fc为30 MPa、40 MPa、50 MPa时，结构柱跨中的y轴最大位移分别为25.32 mm、25.05 mm和24.63 mm。3种不同强度等级混凝土结构柱的最终变形基本相等，其原因是混凝土是脆性材料，在爆炸荷载下会瞬间达到极限拉应变而发生破坏，丧失承载力，不能很好地发挥强度优势。

图11 不同混凝土强度等级的柱跨中y方向最大位移时程曲线Fig.11 Time course curve of span column with different concrete intensity grade in maximal displacement along Y direction

5）混凝土截面尺寸的影响。

对3种不同截面尺寸的构件模型进行对比分析，模型参数如表5所示。

图12给出了不同混凝土截面尺寸结构柱跨中的y方向最大位移时程曲线图，混凝土截面长度L为800 mm、1 000 mm和1 200 mm时，钢筋混凝土结构柱跨中的y轴最大位移分别为25.05 mm、13.32 mm和9.69 mm。随着混凝土截面长度的增加，混凝土体积增大，混凝土抗剪、抗压和受弯能力提高，提升了钢筋混凝土结构柱的抗爆性能。

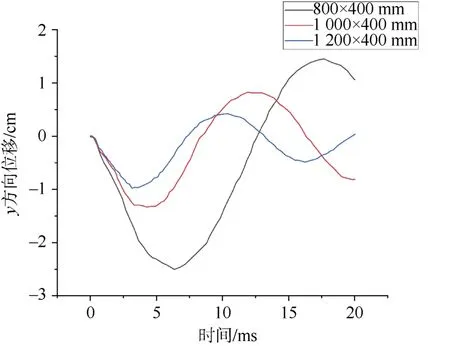
图12 不同混凝土截面尺寸的柱跨中y方向最大位移时程曲线Fig.12 Time course curve of span column with different concrete sectional dimension in maximal displacement along Y direction

表5 各工况的数值模型参数Table 5 Parameters of numerical models in each working condition

3 结束语

1）根据有限元仿真模拟数值结果得出爆炸冲击波峰值Pcr=4.75 MPa，理论公式计算得出爆炸冲击波峰值Pcr=4.67 MPa，有限元仿真模拟数值结果和理论公式计算结果相差 1.7%，验证有限元仿真模型的可信性。

2）有限元模拟得到爆炸荷载作用下钢筋混凝土结构柱的最大动位移为25.05 mm，与理论公式计算结果23.6 mm 非常接近，验证了有限元仿真模型的正确性。

3）混凝土的强度等级为 30 MPa、40 MPa、50 MPa时，钢筋混凝土结构柱跨中的y轴最大位移分别为25.32 mm、25.05 mm和24.63 mm。不同强度等级钢筋混凝土结构柱的最终变形基本相等，结果得出：在爆炸荷载下混凝土会瞬间达到极限拉应变而发生破坏，丧失承载力，不能很好发挥混凝土强度优势。

4）混凝土截面长度为 400 mm、800 mm 和1 200 mm时，钢筋混凝土结构柱跨中的y轴最大位移分别为25.05 mm、13.32 mm和9.69 mm。随着混凝土截面长度的增加，混凝土体积增大，混凝土抗剪、抗压和受弯能力提高，提升了钢筋混凝土结构柱的抗爆性能。

5）钢筋混凝土结构动态响应分析表明钢筋混凝土结构具有良好的抗爆性能，有限元仿真模拟数值结果可为钢筋混凝土结构的抗爆设计、抗爆加固和结构选型提供依据[12-15]。