基于粒子群优化粒子滤波和CUDA加速的故障诊断方法

曹 洁 李 钊 王进花 余 萍

1(兰州理工大学电气工程和信息工程学院 甘肃 兰州 730050)2(甘肃省制造业信息化工程研究中心 甘肃 兰州 730050)

0 引 言

随着以风力发电为代表的清洁能源快速发展，风电机组的装机规模快速增长。如何保证风电机组安全稳定的运行，已成为不可忽视的问题。变桨距系统作为风电机组运行的关键，能够保证高风能利用系数、减轻干扰载荷和风力制动。因此，对变桨距系统进行故障诊断可以有效地避免重大事故的发生，提高运行可靠性，降低运营成本[1]。但受环境影响，变桨距系统存在各类信号扰动和随机噪声，导致故障诊断的准确性不高[2]。

粒子滤波(Particle Filter，PF)由于其适用于非线性非高斯系统，在故障诊断领域得到了广泛的研究和应用[3]。但是算法存在粒子退化和实时性问题，不利于故障诊断的快速响应。针对粒子退化问题，将粒子群优化算法(Particle Swarm Optimization，PSO)引入粒子滤波算法中得到粒子群优化粒子滤波算法，使得粒子向状态后验概率密度高值区移动，改善粒子退化问题[4]。针对实时性问题，文献[5-6]提出了基于图像处理单元(GPU)加速的并行粒子滤波算法，提高了算法的执行速度。文献[7]基于GPU存储架构提出一种共享内存系统重采样，显著提升了粒子滤波的运行速度。文献[8]提出了基于GPU的粒子滤波并行算法，并应用于目标跟踪，在不降低跟踪准确性的同时，提升了跟踪算法的速度。文献[9]提出了GPU加速的粒子群优化粒子滤波算法，提升了算法的速度。文献[10]为解决移动机器人故障诊断实时性问题，提出一种并行化粒子滤波器，减少了故障诊断的反应时间。文献[11]使用CUDA(compute unified device architecture)在GPU上加速粒子滤波和辅助粒子滤波，并应用于工业控制，获得了相比物理过程两个数量级的加速。由于粒子间的相互作用，重采样方法的有效并行实现是一个挑战。文献[12-13]提出了局部重采样，将全部的粒子划分为多个子集，减少重采样对权值的全局操作，从而提升算法的并行性。文献[14-15]分析了Metropolis重采样和拒绝重采样在GPU上的并行实现，并将这两种方法与多项式、分层和系统重采样进行比较，获得了更快的执行速度。但是以上方法存在全局内存的非合并访问问题，阻碍了重采样有效并行化，不利于算法执行效率。

针对上述问题，本文设计并实现了一种基于CUDA的PSOPF并行算法，同时提出了一种合并访问全局内存的拒绝重采样算法，充分利用GPU的计算性能，提高算法的执行速度。在此基础上，利用PSOPF并行算法结合残差平滑法对风电机组变桨距系统进行故障诊断。

1 粒子群优化粒子滤波

1.1 粒子滤波原理

假设系统动态空间模型描述如下：

状态方程：

xk=f(xk-1)+wk

(1)

量测方程：

yk=h(xk)+vk

(2)

式中：xk为k时刻系统的状态值；yk为k时刻的系统观测值；f和h为非线性函数；wk和vk分别为系统噪声和观测噪声。

粒子滤波算法是一种基于蒙特卡洛仿真的近似贝叶斯滤波算法，通过从后验概率中抽取的随机粒子来表达其分布：

(3)

(4)

当式(3)和式(4)随着测量值递推更新时，可通过粒子集的加权平均近似后验概率密度。

1.2 算法步骤

粒子群优化算法由Eberhart和Kennedy于1995年提出，其原理是利用群体中个体的运动来探寻问题求解空间。群体中的每个个体都将自己的经验贡献给群体的发展，并利用群体的全局经验进行自身的发展。因此，信息在两个方向进行传递，分别为从群体到个体和从个体到群体。算法以随机初始化的粒子群作为起始，通过迭代寻优使粒子群找到最优解。在每次迭代中，每个粒子的速度Vi(t)和位置Xi(t)根据先前个体的最优解XPbest(t)和群体的最优解XGbest(t)进行更新：

Vi(t+1)=wVi(t)+c1r1(XPbest(t)-Xi(t))+

c2r2(XGbest(t)-Xi(t))

(5)

Xi(t+1)=Xi(t)+Vi(t)

(6)

式中：i=1,2,…,N，N为群体的粒子数；t为当前迭代次数；w为惯性系数；c1和c2称为学习因子，是非负常数；r1和r2为介于(0，1)区间的随机数。

粒子群优化粒子滤波算法利用PSO的寻优能力对粒子采样过程进行优化，使粒子集趋向于后验概率密度较高的区域运动，并将最新的观测值引入采样过程，定义适应度函数为：

(7)

式中：R为观测噪声；ynew为最新测量值；ypre为预测值。具体步骤如下：

步骤2执行PSO算法。

① 随机初始化粒子的位置和速度。

② 初始化个体最优XPbest(t)和全局最优XGbest(t)。

③ 根据式(7)计算每个粒子的适应度值f(xi)。

④ 对比和更新个体最优XPbest(t)和全局最优XGbest(t)。对每个粒子，将其适应度值与个体最优XPbest(t)相比较，若较好，则替换个体最优。再将每个粒子的个体最优XPbest(t)与群体的全局最优XGbest(t)相比较，若较好，则替换全局最优。

⑤ 根据式(5)和式(6)更新粒子每个粒子的状态。

⑥ 判断是否满足结束条件，若不满足，则返回到③。

步骤3计算粒子的重要性权值并归一化。

(8)

步骤4重采样。

步骤6计算状态估计值：

(9)

2 基于CUDA的PSOPF算法

2.1 CUDA并行计算架构

CUDA是采用基于单指令多线程(Single Instruction Multiple Thread，SIMT)的细粒度并行模型[16]，其基本编程模型如图1所示。其中：CPU作为主机，负责处理串行任务和流程控制；GPU作为协处理器，负责执行并行化任务。CUDA通过调用核函数(kernel)执行并行计算任务，并将线程组织成线程块(block)和线程网格(grid)形式。线程通过线程束(warp)调度执行，一个线程束由连续的32个线程组成，每个线程束中的线程同时执行。线程可以从多个内存空间访问数据：私有寄存器，一个线程块内所有线程拥有的共享内存，以及GPU上的全局内存。此外，所有线程都可以访问另外两个只读存储空间：常量内存和纹理内存。所有这些内存类型都有不同级别的延迟和带宽，因此需要正确选择要使用的内存级别。

图1 CUDA编程模型

全局内存的访问以32、64或128字节为单位，并且以32字节为基准对齐。当线程束中所有线程访问连续且对齐的内存空间时，则所有访问可以合并为一次内存读取。如果内存地址不在同一内存区段中，则无法合并访问，内存访问性能急剧下降。并且，当同一线程束中的内存访问不连续时，尽管线程不需要这些访问之间的数据，但这些数据仍然会被传输，浪费了内存带宽。因此，为了获得好的数据吞吐量，需要通过合并访问将大量的内存获取请求合并，减少内存获取次数。

2.2 基于CUDA的拒绝重采样

算法1拒绝重采样算法

for i=1:N

j=i

u～U[0,1]

while u>wj/sup w

j～U[1,…,N]

u～U[0,1]

end for

其中：xnew是重新采样后的新粒子集；u是服从0到1之间均匀分布的随机实数；j是服从1到N之间均匀分布的随机整数；j是在k时刻所选粒子的索引，该粒子是在k+1时刻的粒子i复制的祖先。

拒绝重采样可以作为单个CUDA内核函数调用实现，使每一个线程对应一个粒子，线程为其代表的粒子选取和复制祖先。拒绝重采样在随机抽选粒子时，存在非合并的全局内存访问。对于较大的粒子数，非合并访问次数增多，导致算法执行效率降低。考虑到线程束中线程在同一内存区段上执行读/写操作能够避免非合并的内存访问，提出改进的拒绝重采样算法，其伪代码如下：

算法2改进的拒绝重采样算法

for i=1:N

j=i

s～U[1,…,Scount]

while u>wj/sup w

j～U[(s-1)*Ecount+1,…,s*Ecount]

u～U[0,1]

end for

其中：s为全局内存中一组固定数量的连续区段，最小的s为单个内存区段，最大的区段为跨越权值数组的所有区段的集合。设Esize是一个权值所占字节大小，Ssize为一个s区段所占字节大小；Scount是s区段的数量，则Scount=Esize×N/Ssize。Ecount是一个s区段中权值的数量，则Ecount=Ssize/Esize。j是服从的s段中第一到最后一个元素索引之间均匀分布的随机整数；s服从第一个到最后一个s区段索引之间均匀分布的随机整数。为方便线程和全局内存对齐，粒子数N的值设为2的次幂。

2.3 基于CUDA的PSOPF并行算法

通过对PSOPF算法的并行性分析，采取线程与粒子一一对应的思路，实现基于CUDA的PSOPF并行算法。具体实施思路为：创建与粒子数相同的线程数，并分配相应的存储空间，每个线程执行一个粒子的运动计算。PSOPF算法流程中更新全局最优和计算状态估计值会产生粒子间的数据关联，无法完全并行化。本文采用并行规约算法寻找极值和求和运算，每个线程处理一个粒子，提高并行度，以充分发挥GPU并行计算性能。根据PSOPF算法的计算流程，制定的基于CUDA的PSOPF并行算法流程如图2所示。

图2 基于CUDA架构的PSOPF并行算法流程

3 实验结果及分析

3.1 算法性能测试

为验证本文算法的精度和运行时间等性能，采用一维非线性系统模型在CPU和GPU平台上进行实验仿真，并与PF以及PSOPF算法进行对比。实验所采用的计算平台如表1所示。

表1 计算平台

状态模型和量测模型如下：

(10)

(11)

式中：系统噪声wk为符合N(0,10)分布的高斯噪声；测量噪声vk为符合N(0,1)分布的高斯噪声。均方根误差公式为：

(12)

令粒子数N=256，单次仿真结果如图3和图4所示。分别令粒子数N=128和N=256，进行50次蒙特卡洛仿真并取平均值，得到三种算法的均方根误差对比如表2所示。

图3 不同算法的状态估计结果

图4 不同算法的RMSE对比结果

表2 不同算法RMSE对比

从图3、图4和表2可以看出，由于增加了PSO算法的寻优过程，引入粒子群优化的粒子滤波算法的均方根误差明显小于标准PF算法。而采用改进拒绝重采样的本文算法跟踪效果最好，均方根误差小于PSOPF算法，说明其估计精度最高。

在不同粒子数时本文算法的运行时间如表3所示。

表3 本文算法运行时间对比

由表3可以看出，GPU的运行时间明显小于CPU。算法在GPU上的运行时间始终小于1 s，而CPU的运行时间可达数秒，因此基于CUDA执行的本文算法能够显著地提高运行速度。并且随着粒子数的增加，运行时间逐渐增加，GPU的增加幅度明显小于CPU。在粒子数较多时，能够获得较好的计算性能。

在不同粒子数时分别在CPU和GPU上执行PSOPF算法和本文算法，获得加速比曲线如图5所示。

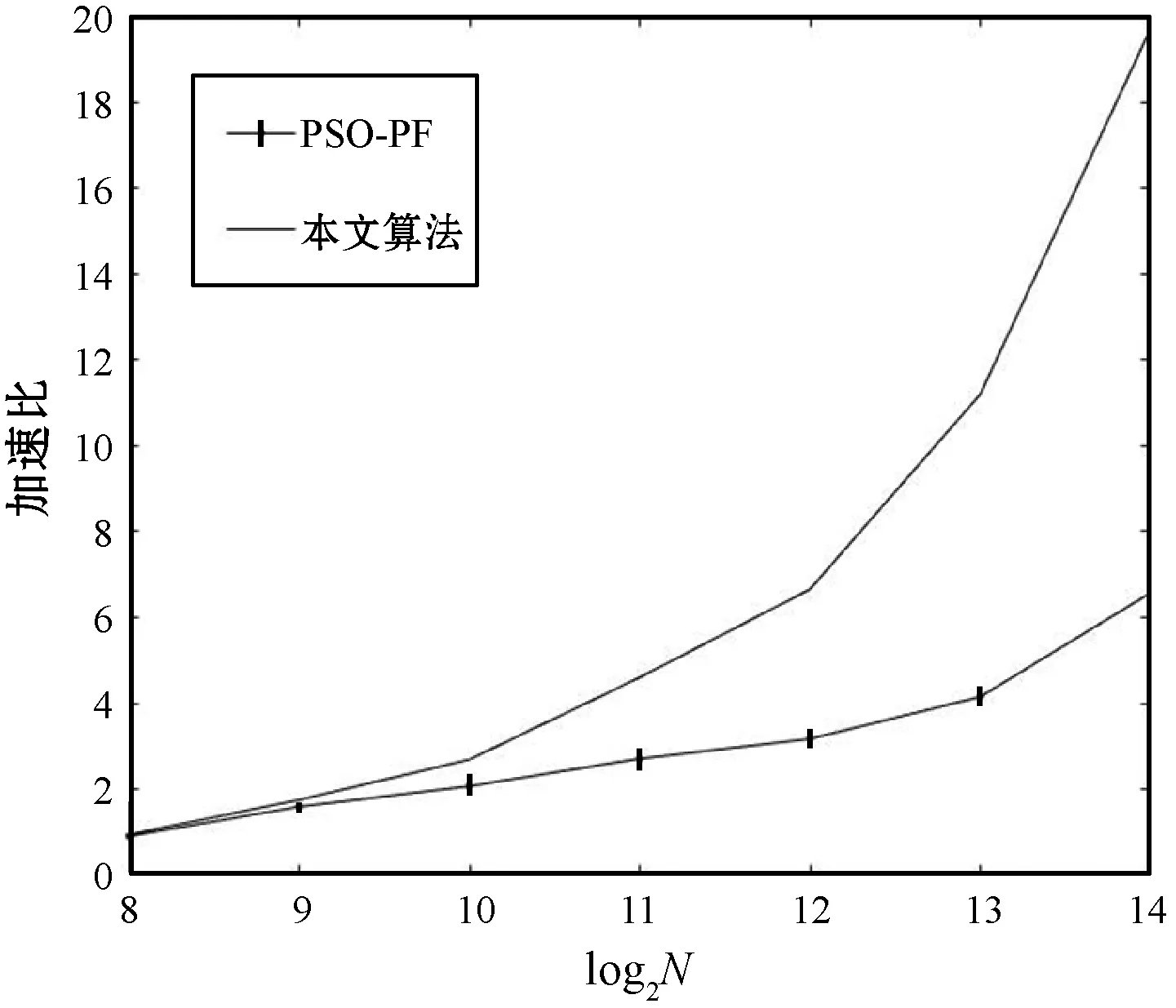
图5 不同算法的加速比对比

由图5可见，随着粒子数从28增加到214，本文算法的加速比增长快于PSOPF算法，这是由于随着粒子数的增加，算法计算量增加，采用改进拒绝重采样的本文算法避免了非合并访问，提高了GPU内存使用效率，显著地提高了算法的实时性。

3.2 变桨距系统的故障诊断仿真与分析

风电机组变桨距系统由三个相同且独立的桨距控制器组成，每个桨距角控制器被建模为实际的桨距角β与其参考值βref间的闭环传递函数。βref为闭环传递函数的输入，由系统的桨距角控制器提供；β为传递函数的输出，作为桨距角的测量值。实质上，变桨距系统是一个活塞伺服系统，可以通过二阶传递函数建模[17]：

(13)

(14)

表4 故障模式表

变桨距系统的故障诊断原理如图6所示，采用本文提出的改进粒子滤波算法，对应模式M0-M3，分别为每个模式配置一个粒子滤波器进行状态估计。计算各个模式的桨距角估计值y(m)(m=0,1,2,3)，对比系统的实际测量值y获得残差e(m)，并根据式(15)计算最近M时刻内的残差平滑值d(m)。

(15)

图6 变桨距系统故障诊断原理框图

首先进行故障检测，设置残差阈值δ(δ>0)，当残差平滑值d(0)大于阈值δ时，则判断系统发生故障，否则判断系统无故障。检测到故障发生后，通过比较每个故障模式的残差平滑值d(m)(m=1,2,3)的大小来进行故障隔离，若其中某一个模式的残差平滑值最小，则判断系统发生了该模式故障。

根据正常模式的系统模型计算当前时刻的残差平滑值d(0)，当d(0)大于阈值时，则检测到系统发生故障。系统正常运行和发生故障M1-M3时的残差曲线如图7所示。

(a) 系统正常运行时的桨距角残差

(b) 系统发生故障M1时的检测结果

(c) 系统发生故障M2时的检测结果

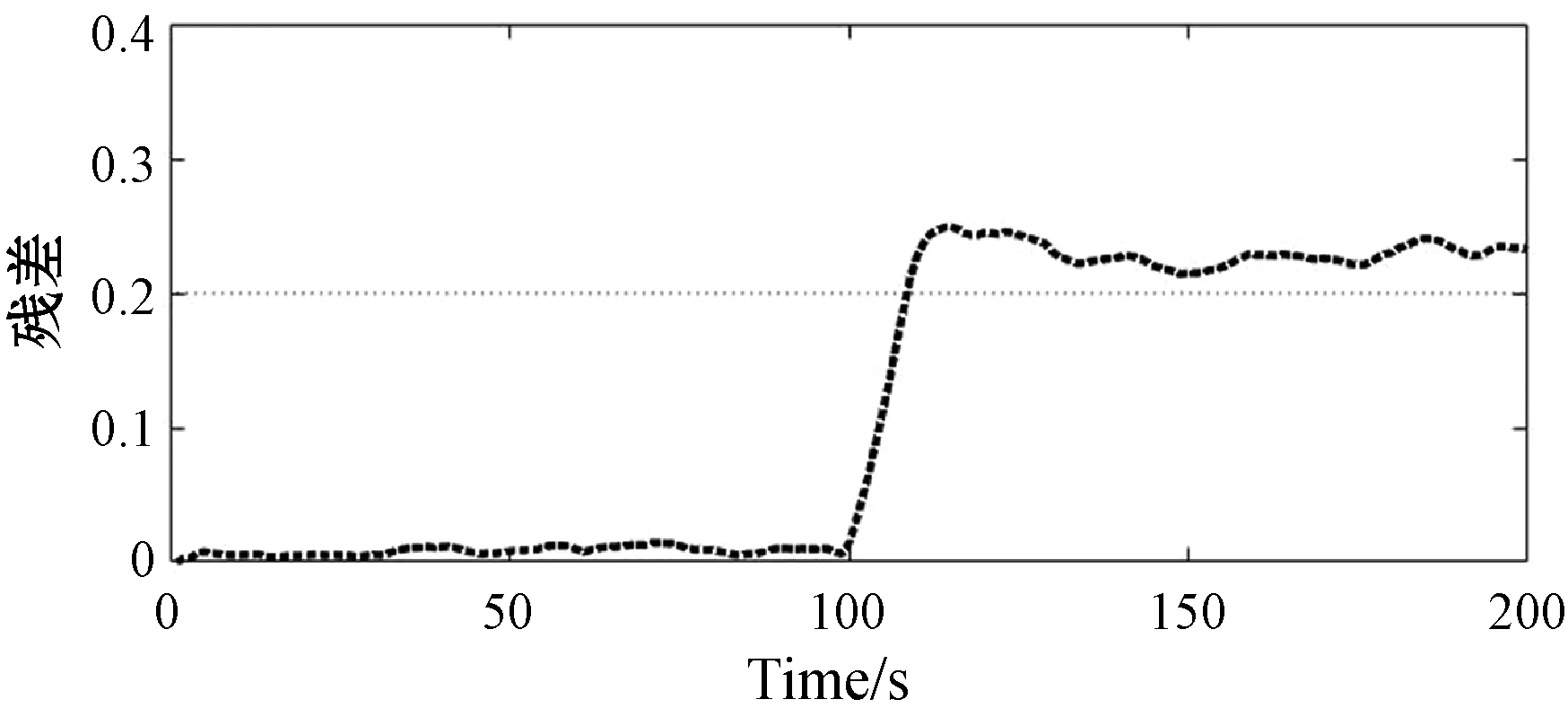
(d) 系统发生故障M3时的检测结果图7 不同故障的诊断结果

从图7(a)可见，当系统正常运行时，桨距角残差基本为零。从图7(b)-(d)可以看出，对于故障M1-M3，系统无故障时的统桨距角残差幅值较小，且变化比较平稳；当故障发生后，残差变化剧烈且幅度高于阈值，因此判断故障发生。

检测到故障后，启动故障M1-M3模型进行故障隔离，结果如图8所示。

(a) 系统发生故障M1时的隔离结果

(b) 系统发生故障M2时的隔离结果

(c) 系统发生故障M3时的隔离结果图8 不同故障的隔离结果

由图8(a)可见，当检测到故障M1发生后，由于M3为桨距角传感器偏差故障，起始残差在0.3左右。M1和M2的残差曲线较为相似，但M1的残差是最小的，故判断为M1故障。同理分析图8(b)和(c)可见，当系统实际状态与某故障模型匹配时，其残差平滑值相比其他故障模型较小，则判断该故障模式发生。

4 结 语

本文基于CUDA架构设计实现了一种GPU加速的PSOPF并行算法，通过分析PSOPF算法的并行性，采取线程和粒子一一对应的方式实现并行化算法，运行速度得到显著提升。利用改进的拒绝重采样并行算法，解决全局内存读取时出现的非合并访问问题，提高了PSOPF并行算法在GPU上的执行效率，并将其应用到风电机组变桨距系统故障诊断中。实验结果表明，所提出的改进的PSOPF并行算法有效地提高了实时性，是一种进行故障诊断有效的方法。

下一步工作将设计并实现基于CUDA的多模型粒子滤波故障诊断方法，通过故障诊断的并行化，以提高故障诊断的实时性能。