壶西大桥斜拉索拉力检测与安全评估研究

王伟芳

摘要：斜拉索是支撑斜拉桥整个桥面板主梁的主要构件，不论是在桥梁施工期间，还是营运阶段，将主导斜拉桥整体结构的安全性。因此，利用斜拉索力学变化对斜拉桥安全进行评估是可行的方法。文章以简便的振动法进行斜拉索振动试验，并经由斜拉索局部自然振动频率推算索力，用以分析各钢缆受力情形及评估斜拉桥的安全性。

关键词：斜拉桥;拉索;检测;安全评估

中图分类号：U446 文献标识码：A DOI：10.13282/j.cnki.wccst.2020.11.040

文章编号：1673—4874（2020）11-0145—03

0引言

斜拉桥通车后，斜拉索就成了安全维护最困难的主构件之一。由于斜拉索的细长比相当大，柔软低阻尼，以及抗挠能力差，在风致振动、常时车流，甚至在环境振动下都可能增加相当大的反复挠曲应力而导致疲劳损伤引发断裂。斜拉索封口松动、锚定端锚受损，以及根部保护管破坏造成内部绞线腐蚀等问题，皆大大地缩短斜拉索的寿命，甚至有可能影响到整座桥梁的安全。另外，车流与风力等外力时刻作用于斜拉索上，即使将已损坏的钢缆置换，也不能保证日后不再继续发生同样的损伤，斜拉索随时会因振动而损坏。因此斜拉索在常时车流、偶时地震或台风的力学作用下，产生的疲劳现象、拉力损失变化等，都是斜拉桥潜在的危机，也是平常检测维护或长期监测的重点。

1项目概况及检测安排

壶西大桥为柳州市区的跨江主桥，采用大跨径双塔双索结构系统，桥塔为H型钢筋混凝土结构。主跨与边跨各配置14组斜拉钢缆，除两跨最外侧一组各为4根外，其余各组均为两根钢缆组合，共计60根钢缆支撑整座桥梁。最靠近A1桥台的钢缆编号为B101与B101A，钢缆B114则为边跨内最靠近P1桥塔的钢缆;主跨内最靠近P1桥塔的钢缆为F114，而F101A与F101则是最靠近P2桥柱的钢缆。整座斜拉桥斜拉钢缆以单索面双缆混合扇形配置。

本文将针对壶西大桥全部钢缆在常态车流下进行振动检测，其中钢缆分为两种规格：一种是15.2mmφ，-ASTM A416—90a 270级的低松弛钢绞索;另一种为15.7mmφ-BS-5896170级的第二级低松弛率钢绞索。钢缆型式分为Tyl3e A与Tyl3e B两种，TypeA最大排列91支钢绞索，共有46根;Type B最大排列61支钢绞索，共有14根。合计60根钢缆。

2斜拉索试验与分析探讨

在实际设计与施工中，计算钢缆拉力的方法多是利用钢缆自然频率推得拉力值，因此检测钢缆拉力必须配合振动测量试验，再由频率反推拉力值。本文将针对壶西大桥全部钢缆，在未封闭桥梁的常态车流下进行振动检测试验，如图1所示。

2.1钢缆震动测量及分析

壶西大桥共有60根钢缆分布全桥跨度内，因受限于仪器频道数与信号衰减等因素，将60根钢缆分成15次依序进行测量，每一次测量时间皆为10min，取样频率为100Hz，取样点共60000点，其他钢缆测量方式相同，以此类推。另外，受限于现场环境无法封闭车道与节省经费，因此，本试验并未使用空中作业车，故钢缆缆身测点仅设定在距桥面板高度2.5m处。另外，为不破坏钢缆HDPE外套管，必须先依钢缆外径制作一对半圆形夹具，夹具上的平板可放置三个单轴向传感器分别测量钢缆三方向振动反应。由于钢缆振动量相当大，配置在较低位置所测得的反应虽较小，但并不影响分析结果。

2.2钢缆拉力分析

为求得钢缆振动频率，可将测量所得振动历时反应经由傅里叶变换求得各钢缆的频谱图，分别为主跨内靠南下车道侧的较短索（F114R）、中长索（F107R）与长索（F101R）钢缆的频谱图。由于钢缆为圆形对称断面，因此，合理地推估钢缆X向与y向的振动频率应相近，但存在于钢缆的非线性效应尚有所差异。另外，钢缆Z向振动则容易受到桥面板互制参数振动的影响，而不易分析钢缆低频的振态。因此，由各频谱图中非常容易分析出钢缆高振态自然振动频率，相反的，前几个低振态频率反而较难判断。这些情况都是因为桥面板振动所造成的干扰效应，由于钢缆与桥面板是连结在一起的，钢缆可能测量到的振态频率不仅是钢缆局部振态，同时也包含桥面板振态。因此，通过同时测量钢缆及桥面板振动的方式，过滤出钢缆低频部分的局部振态，以免有误判钢缆频率的情况发生。

另外，本研究选取钢缆X向前5个振动频率计算靠南下车道侧钢缆与靠北上车道侧钢缆共60根的索力，计算方式包括：

（1）识别钢缆前5个振态频率，依弦理论分别计算索力，并取此5个索力的平均值作为该钢缆拉力;（2）利用前5个频率的频率差值分别计算索力，并取此4个索力的平均值作为该钢缆拉力;（3）使用前5个振态频率依梁理论分别计算索力，并取此5个索力的平均值作为该钢缆拉力。

若以梁理论计算值为基准，比较各方法计算结果可知，此三种方法求得各索索力的差异性皆维持在0.5%范围以内，显示此三种计算方式差异性并不大。但是，在钢缆频率判定方面，频率差法较容易获得正确的频率值，不致误判钢缆局部频率。因此，在实际应用上，此三种计算索力的方法皆可使用，但取较多的振态频率计算索力，再求其平均值应是较可行的方法。另外，在计算过程中也发现，对于长索而言，如F101～F103等钢缆，使用第一振态频率以梁公式计算索力时，其结果与其他振态所计算出的结果差异较大，反而使用高振态频率计算索力有较佳的收敛结果。这是因为长索的非线性效应非常明显，而且若是以非线性精算公式计算索力，长索被归类到第二类或第三类索型，必须采用高振态计算索力，若仅利用第一振态频率计算较长索的索力，可能会存在较大的误差。因此，建议使用以上三种方法计算索力，取较多振态频率计算索力再取平均值，应可降低长索计算拉力造成的误差。

3损伤评估

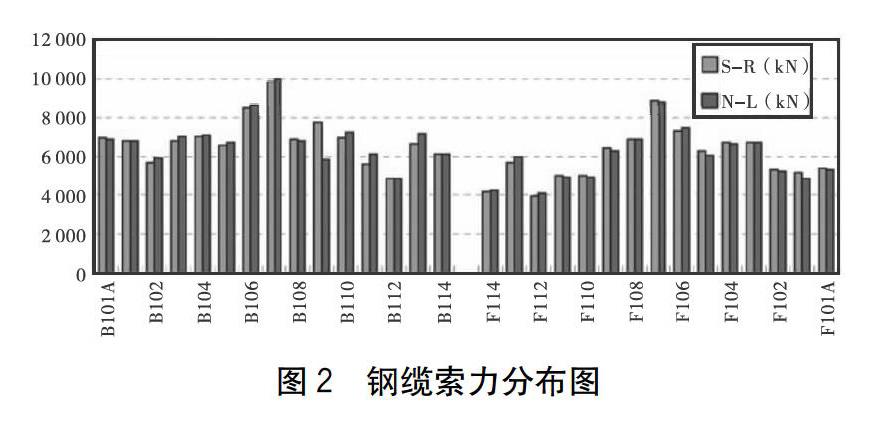
一般而言，结构损伤定位的指标常用的有模态曲率指标、模态柔度指标等，但这些指标都有一个同样的问题，即需要测量出桥梁的振动模态。因此，对现场测量技术与系统识别技巧方面的要求较高，同时，测量精度也较难掌握，尤其是需要高振态参数数据。上述损伤指标方法虽可应用于斜拉桥的损伤定位，但斜拉桥为高度静不定结构，复杂的钢缆系统使得斜拉桥在建模与分析时，常因非线性效应而造成极大的误差，而此效应也间接增加对斜拉桥安全评估的困难度。实际上，斜拉桥依其受力情形分析，橋面板主梁与钢缆是较容易受损的主构件，而钢缆与桥面板连结在一起，两者具有相当大的关联性。因此，若能通过钢缆测量试验获得索力，并掌握钢缆受力变化情形，应可进一步评估桥梁的安全性。钢缆索力分布图如图2所示。

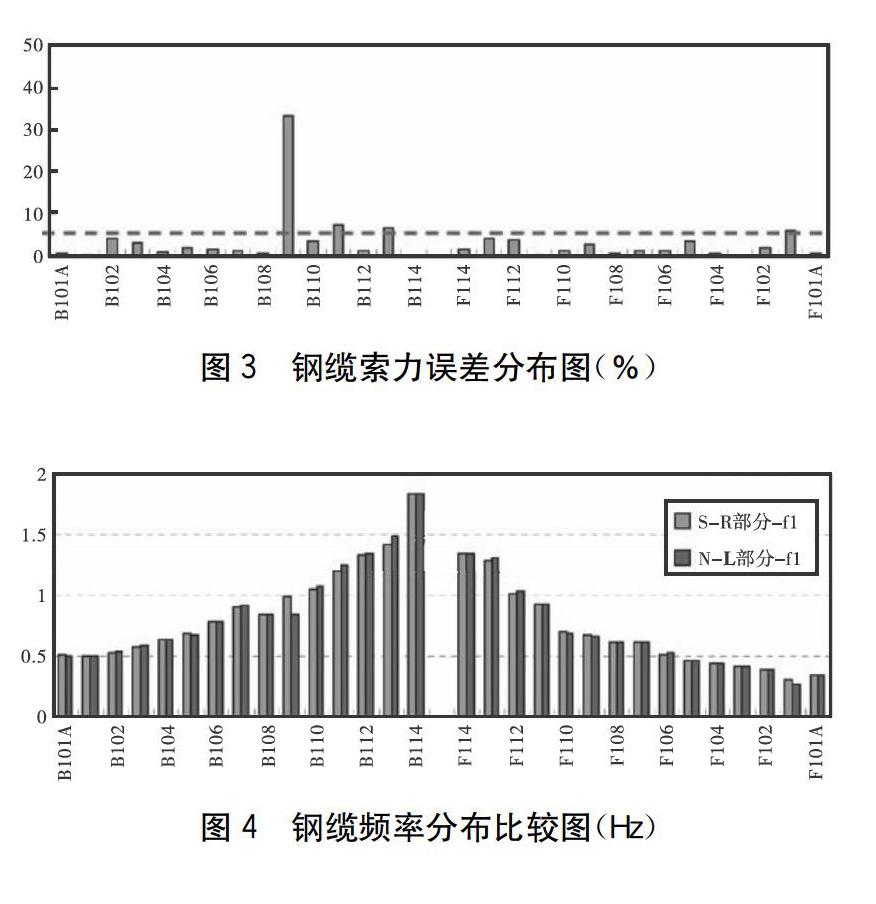
图2为60根钢缆利用梁理论计算的索力分布情形。理论上，同一位置的左右两侧钢缆力量应较为接近，但左右两侧差异性若超过某一容许误差，则此处钢缆可能有异常的现象。本文假设以5%为容许误差，并以L侧钢缆拉力为计算基准，若超过这一容许误差值表示该钢缆拉力存在异常现象。如图3所示，超过此一容许误差的钢缆为：B109R与B109L索相差33.40%;B111R与B111L索相差7.65%;B113R与B113L索相差6.99%;F101R与F101L索相差6.09%。另外，由图3中亦可得知，若钢缆索力异常，则TI值差异变化相当大，故拉力指标对损伤相当敏感，应适用于损伤指标。因此，针对壶西大桥案例而言，对于以此种钢缆排列方式的斜拉桥，可利用此拉力指标作为损伤异常的分析参数，并合理地制定容许百分比误差，当同一位置左右两侧钢缆力量超过这一误差值，则须针对此钢缆作进一步检测评估，而且钢缆索力异常处的桥面板主梁也须一并检测。

另外，图4为各钢缆第一个振态频率分布比较图，各振态频率分布图呈现近似钟型分布。因此若有钢缆频率异常情况，则各振态频率分布图可能为非钟型分布，也可依此初步评估损伤位置。但由图4可知，若仅以此频率分布情形作为损伤情况评估的依据，则可能不敏感。

4结语

本文主要是应用现场微动试验测量壶西大桥钢缆振动反应，求得钢缆的各振态自然频率值，再由简单的拉力计算公式求得钢缆预力近似值，评估斜拉桥钢缆索力变化情形。另外，本文利用所有的已知钢缆拉力值，建立一个评估索力异常的拉力指标，通过这一指标，可进一步检核主梁的安全性。因此，本文的结论如下：

（1）使用微動试验即可求得钢缆自然频率，不须封闭桥梁，也不须以较昂贵的试验方法进行试验，微动试验较经济且方便。

（2）测量钢缆振动时，建议测量钢缆两个以上的方向，并同时测量桥面板主梁的振动，可通过此方法正确地判断出钢缆各局部振态自然频率，同时也可了解到桥面板主梁对钢缆振动的影响。

（3）若仅以第一振态频率计算拉力，可能会产生较大的误差，尤其是对于中垂效应非常明显且索长非常长的钢缆，应属于非线性精算公式分类的第二类或第三类型式，建议取前五个振态分别计算其拉力值，即可求得较佳的拉力收敛值。

（4）对于壶西大桥而言，若能求出各索力，则可经由适当的拉力指标，进行斜拉桥钢缆拉力异常的评估，未来也可依此评估桥面板主梁损伤程度。