循环温度作用下饱和黏土中摩擦型桩变形特性研究

陆浩杰，吴 迪，孔纲强,2，刘汉龙

(1.重庆大学土木工程学院，重庆 400045；2.河海大学土木与交通学院，江苏，南京 210024)

能量桩是将传统桩基与地埋式换热管相结合，可以起到支撑上部建筑荷载与浅层地热能能量交换的双重作用[1－2]。能量桩在运行过程中，温度变化会影响桩基的力学特性，引起附加应力和变形，从而影响桩基承载性能。针对能量桩的热-力学特性，相关学者开展了系列研究：Laloui等[3]通过对制热过程中桩体的温度、轴向应变等进行量测，分析了温度荷载作用下能量桩的力学特性；结果表明当上部荷载较小时，能量桩应力、应变表现为热弹性，即温度荷载不会引起不可恢复的应力和应变。Bourne-Webb等[4]研究了不同温度荷载下桩体的受力和变形特性，结果表明在制热过程中桩体内会产生较大的压应力；而在制冷过程中桩体内会产生拉应力。Wang等[5]针对一根摩擦型能量桩的桩侧极限摩阻力变化进行了监测，结果表明摩擦型能量桩的热交换作用并不会影响摩擦型能量桩的容许承载力。Goode和McCartney[6]探究了桩端约束条件对能量桩承载性能的影响，结果表明在压实的淤泥土中，能量桩制热会引起摩擦型能量桩极限承载力的显著提升；而在干砂中，能量桩制热时引起的摩擦型能量桩极限承载力的变化可以忽略不计。桂树强和程晓辉[7]针对温度荷载引起桩体应力-应变重分布对桩体结构响应的影响进行了分析，结果表明桩身的应力-应变重分布不仅会导致制冷条件下桩体下部出现较大拉应力，还会导致桩-土界面产生弹塑性变形。

已有研究绝大多数都是针对单次温度荷载作用下能量桩的力学特性[8―12]，针对循环温度荷载作用下能量桩力学特性的研究则仍然相对较少[13―15]。基于数值方法，Olgun等[13]分析了30轮循环温度荷载作用下，桩体温度和桩顶位移变化规律，认为当能量桩承受循环温度荷载时，土体温度对能量桩换热效率的影响十分明显，且可以认为温度循环过程中桩身长度为纯弹性变化。基于离心机模型试验方法，Ng等[14]研究了循环温度荷载作用下钻孔灌注能量桩和预制能量桩的桩顶位移的变化规律，结果表明：钻孔灌注能量桩会产生累积的桩顶沉降，而打入式能量桩在循环温度作用后观察到了桩顶的轻微上移。Nguyen等[15]开展砂土中摩擦型能量桩的模型试验，研究了摩擦型能量桩在长期温度荷载作用下的桩顶位移变化规律，结果表明：在工作荷载下，循环温度荷载作用下能量桩会产生不可逆的桩顶位移，且桩身轴向应力随循环次数的增加而增加。

当黏土温度变化时，其力学特性也会发生改变[16]，如当黏土温度升高时，黏土抗剪强度降低，且正常固结黏土还会产生不可恢复的收缩变形。当能量桩埋设在黏土地基中，能量桩的运行会改变桩周土体的温度，引起桩周土体力学性质的改变，从而对能量桩的承载特性造成影响。因此，黏土中能量桩的承载特性相对更为复杂。但是，目前对黏土中能量桩的研究仍相对较少。Ng等[17]研究了不同超固结比黏土中摩擦型能量桩的热-力学特性，结果表明：正常固结黏土中能量桩桩顶的累积位移更为明显，且随着超固结比的增大而减小。Stewart和McCartney[18]研究了粉质黏土中端承型能量桩桩-土界面的相互作用机理，结果表明：在连续的温度循环过程中桩顶会产生下降位移。Yavari等[19]研究了不同轴向应力作用下黏土中能量桩的力学特性，结果表明：随着桩顶载荷的增大，黏土蠕变速率会增加。Wu等[20]研究了黏土中能量桩与传统非制热桩之间的相互作用，结果表明：能量桩与相邻非制热桩在有桩帽时会产生明显的相互影响作用，从而改变能量桩的位移特性。上述研究成果对于深入了解黏土中能量桩的变形特性与机理起到了积极作用；然而，已有研究绝大多数都是针对单次或少量(<5次)循环次数情况下的热力学特性变化，长期循环温度作用下黏土中摩擦型桩的变形特性与机理仍需要进一步深入研究。

因此，本文开展黏土中摩擦型能量桩变形特性模型试验，研究工作荷载和长期(20次)循环温度作用下能量桩的沉降特性。试验过程中，施加工作荷载和循环温度荷载后，对能量桩的温度和位移及桩周土体的温度和孔隙水压力进行测量；并初步探讨能量桩在长期运行过程中的累积沉降特性。

1 模型试验概况

1.1 试验装置

试验装置包括模型槽、排水板和加载板及砝码等部分。模型槽尺寸为800 mm×400 mm×750 mm，壁厚12 mm，为了增大模型槽的侧向刚度，在模型槽外侧采用钢框架进行约束。模型槽分为上、下两层，中间由螺栓连接，上层高度为 250 mm，主要在土体制备过程中使用，下层高度为 500 mm，用于装载土体及模型桩。模型槽左、右两侧各设置一块20 mm厚排水板，底部设有排水孔，通过硅胶管将模型槽排水孔与水箱连接，通过控制水箱内水位来实现土体内水位的控制。加载板为厚度10 mm的钢板，中间设有孔洞方便模型桩穿过，孔洞直径略大于模型桩直径，砝码为铁块，每块重10 kg。

1.2 模型桩及仪器

模型桩直径24.6 mm，桩长550 mm，有效桩长450 mm。模型桩由空心不锈钢管制成，内、外径分别为21 mm和23 mm，钢管底部用圆锥形的桩帽密封，且在桩顶设置了桩帽；在桩体底部砂土层中垂直放置了内径和高度分别为35 mm和50 mm的钢管且内部无填充物，所以桩端阻力可以忽略不计。为了控制桩体温度，在不锈钢管内部空腔中央埋设换热管，换热管道为内径2 mm的U型铜管；桩身内部不同高度处(见图1)布置 5个热敏电阻(PT1~PT5)，用于测量桩体温度，埋设前用水浴法对每个热敏电阻进行校正。待换热管道和热敏电阻埋设完毕，为了消除仪器、换热管及桩体之间空气热阻的影响，在不锈钢管内部空隙中填充环氧树脂并振捣密实。为了使钢管表面更接近混凝土桩表面，在不锈钢管表面利用环氧树脂粘结一层细砂，最终桩体外径为24.6 mm。通过自由膨胀加热试验，得到本研究中模型桩的平均线性热膨胀系数为15.1 με/℃。

当桩体长径比较小时，桩体混凝土的储热能力会对能量桩的传热特性造成影响[21]，将线热源的假设应用于能量桩欠准确。不过，实际工程应用中能量桩长径比往往并不大。本文统计了目前已开展的能量桩应用与现场试验中能量桩的长径比(长径比范围为8~55)，如表1所示。除现场试验外，目前开展的模型试验当中，Stewart和McCartney[18]采用的模型桩长径比为11，Nguyen等[15]采用的长径比为30，Ng等[17]采用的长径比为19，长径比均在8~55范围内。因此，本文的研究结果(长径比约为18)可以用于分析当能量桩长径比较小时其力学特性的变化规律，而对于长径比较大的能量桩，需专门开展针对性的研究。

土体中仪器包括8个热敏电阻(ST1~ST8)及4个孔压计(PPT1~PPT4)，用于测量土体温度变化及孔隙水压力变化。仪器位置如图1所示。为了测量桩顶沉降变化，桩帽上对称布置2个百分表。

图1 试验布置示意图 /mmFig.1 Sketch of test arrangement

表1 能量桩现场测试研究概况Table 1 Summary of in-situ tests on energy piles

1.3 温控循环系统与尺寸效应

热-冷温控循环系统由保温箱、电加热器、温度控制器和循环泵组成。保温箱容积15 L，内部设有与温度控制器连接的电加热器，功率 2 kW，温度控制器带有温度感应器和显示屏，能够进行目标温度设定来控制换热液体温度变化(精度为0.1 ℃)。制冷阶段通过冰块来给换热液体降温。保温箱内部设有搅拌装置以保证内部换热液体温度均匀。能量桩换热管与保温箱之间通过硅胶管连接，中间通过设置循环水泵实现换热液体在能量桩内和保温箱之间的流动，流速0.3 L/min。硅胶管外侧设有保温层来防止热量散失。换热液体为蒸馏水。

试验系统放置在约15 m2的密闭空间，内部设有空调和风扇，用于室内温度的控制和空气流通，室内不同位置布置4个温度计，试验过程中控制室温稳定在25 ℃。

为了能够通过模型试验反映现场条件下的热力学性能，本文通过模型试验与现场试验之间的几何尺寸差别进行方案设计，采用式(1)来确定每轮温度循环的时间[27]：

式中：F0为傅里叶数；as为土壤导热系数；t为时间；D为桩径。

由于式(1)中时间是无量纲的，因此，模型试验的结果可以用于跟原型试验进行比较。本文采用与Ng等[17]相同的傅里叶数F0，故本文试验条件下每轮温度循环时间取270 min，对应Ng等[17]试验中原型尺寸下，桩径为0.88 m的能量桩，每轮温度循环时长为8个月[20]。

1.4 试验准备工作

试验用土包括厚度450 mm的桩周正常固结黏土及50 mm的桩端砂土，如图1(a)所示。砂土为南京地区长江砂土，黏土为南京地区软黏土，土体参数如表2、表3所示，其中渗透系数根据Zeng等[28]对南京地区软黏土的渗透系数试验得到。

表2 黏土参数表Table 2 Properties of clay

表3 砂土参数表Table 3 Properties of sand

土样制备时，先利用砂雨法进行桩端砂土层的制备填筑，落距为 500 mm，砂土层制备完成后，测得其相对密实度约为69%。砂土层填筑完成后，通过控制水箱内的水位使砂垫层达到饱和状态。

待砂土层饱和完成后，进行桩周黏土层的制备。在填筑黏土前，先将预先干燥后的干燥粉状黏土与水进行混合制得泥浆(含水量达到 2倍液限)，然后将泥浆在真空环境下静置3 h以除去搅拌过程中混入的气泡。待抽真空完成后再将泥浆小心地置入模型槽中(砂土上部)。泥浆达到设计高度后，通过砝码和加载板对土体表面分5级施加荷载，每级荷载大小分别为2.5 kPa、5 kPa、10 kPa、20 kPa和40 kPa，间隔 48 h；在最后一级荷载加载过程中，土体表面安装百分表，记录土体表面沉降量；施加最后一级荷载至沉降稳定后(约 120 h后)卸去表面荷载，随后修整土体表面至设计高度 500 mm，同时在水箱中加水，并保持液面高度始终与土体上表面持平，土样制备完成。使用KD2 Pro热分析仪测量黏土热学参数。

土体制备完成后，进行模型桩和仪器埋设。热敏电阻尺寸为 1 mm×1 mm×2 mm；孔压计为直径1.5 cm，高1.5 cm的圆柱体。在进行模型桩埋设之前，需先使用直径和长度分别为19 mm和500 mm的薄壁土壤采样器在模型桩所处位置的黏土中钻孔，然后，将模型桩竖直插入钻孔并达到预定深度。孔压计的埋设与模型桩类似，但是在孔压计达到预定深度后，利用泥浆将孔压计与钻孔之间的空隙填充以达到密封作用。埋设热敏电阻前，预先将热敏电阻用环氧树脂固定到钢钎(直径 3 mm)上构成热敏电阻序列，随后将热敏电阻序列在设计位置直接插入黏土中并达到设计高度。

待土体中传感器和模型桩埋设完毕之后，土体表面覆盖一层塑料膜(防止水分蒸发)并重新加载至40 kPa进行土体二次稳定，时间约120 h。土体和桩顶布设位移传感器。待土体沉降稳定后，试验准备工作完成。

1.5 试验工况及步骤

试验共包括3组工况，分别为桩基静载试验、能量桩热-力学试验和参照试验；静载试验是为了得到桩基的极限承载力；能量桩热-力学试验是为了研究多次温度循环作用下能量桩的位移特性。特别需要指出，在黏土次固结作用下，桩侧会产生负摩阻力，随着时间增长，即使没有循环温度荷载，桩顶也会产生沉降变形[29]。这意味着能量桩热-力学试验中能量桩桩顶位移的变化由温度循环和黏土次固结两个因素共同造成。为了突出温度循环对能量桩位移的影响，需要开展参照试验来消除次固结对桩体长期沉降的影响。本文试验具体步骤如下：

1)根据《建筑地基基础设计规范》进行单桩竖向静载试验，得到桩基的极限承载力约为367.5 N，本次试验取安全系数等于 2.5，得到工作荷载大小为 147 N[20]。

2)根据上述方法重新制得土体并埋设桩体及仪器，待桩土稳定过程完成后，桩顶施加工作荷载并保持 180 min(为了消除加载对孔隙水压力的影响)。记录各仪器读数作为初始值。保持工作荷载大小不变，使保温箱内的循环液体达到目标温度(45 ℃和5 ℃)，打开循环泵，进行20轮热-冷温度循环(进口水温分别为45 ℃和5 ℃)，单轮循环时间为270 min (热-冷荷载各135 min)。

3)根据上述方法重新制得土体并埋设桩体及仪器，待桩土稳定过程完成后，桩顶施加工作荷载并保持 180 min (为了消除加载对孔隙水压力的影响)，随后继续保持工作荷载1350 min，记录整个过程桩体位移变化。

图2 试验系统布置实物图Fig.2 Physical diagram of system layout

2 试验结果与分析

2.1 能量桩及桩周土体温度变化规律

桩体、桩周土体温度随时间的变化规律如图3所示。当能量桩制热时，桩体及桩周土体的温度上升，在随后的制冷过程中，桩体及土体的温度逐渐下降。本文试验进口水温变化范围是 5 ℃~45 ℃，由图3可知，能量桩桩身温度在10 ℃~40 ℃变化，小于进出口水温的变化范围，这主要是由换热管与桩身仪器之间桩体材料的热阻造成的。由于土壤的热阻，土体的温度变化量小于能量桩的温度变化量，且离桩中轴线越远，土体温度变化量越小。例如，距离桩中轴线1倍桩径处(ST3)的土体温度变化范围为18 ℃~32 ℃，距离桩中轴线2倍桩径处(ST6)温度在22 ℃~28 ℃变化，距离桩中轴线8倍桩径处(ST8)未观察到明显温度变化。

当能量桩承受循环温度荷载作用时，由于本文试验进口水温(分别是 5 ℃和 45 ℃)关于环境温度(25 ℃)对称变化，桩身及桩周土体的温度也基本关于环境温度呈现对称变化，且每轮温度循环过程中桩身及桩周土体的温度变化规律基本一致，这与Olgun等[13]的研究结果一致。

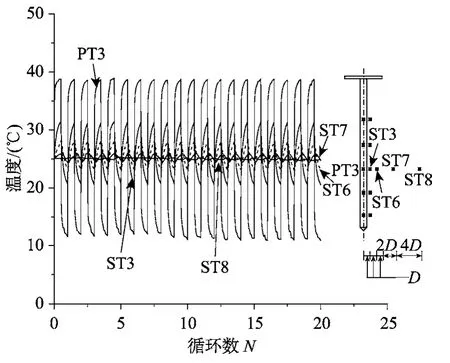
图3 桩、土温度变化关系图Fig.3 Temperature change rule of pile and soil

2.2 桩周土体孔隙水压力变化规律

由于水的热膨胀系数大于土颗粒的热膨胀系数，当温度上升时，水的体积膨胀大于土骨架的体积膨胀，这时土骨架会对水的变形产生约束作用，因此，土体内会产生超静孔隙水压力。当温度下降时，由于水的体积收缩大于土骨架的体积收缩，土体内产生了负的超静孔隙水压力[30]。通过将温度引起的孔隙水压力变化与土体竖向有效应力归一化处理，能够考虑孔隙水压力对土体强度的影响。即当 Δu/σ＇=100%时(σ＇为土体有效应力)，说明孔隙水压力增量等于土体有效应力大小，这意味着土体有效应力为0。

土体中温度变化引起的孔隙水压力变化情况如图4所示。由图4可知，当土体温度升高时，孔隙水压力升高；当土体温度降低时，孔隙水压力降低，这与 Abuel-Naga等[30]的研究结果一致。距离桩中轴线越远，土体孔隙水压力变化量越小。例如，距离桩中轴线1倍桩径处(PPT1)，孔隙水压力的变化幅值约为±10%土体有效应力；而距离桩中轴线更远的2倍(PPT3)和4倍桩径处(PPT4)，孔隙水压力变化幅值分别约为±7%和±3%土体有效应力。这个现象可归因于距离桩中轴线越远，土体温度变化量则越小；温度引起土体中超孔隙水压力的大小与土体温度的变化量呈正比[30]。在距离桩中轴线1倍桩径处，靠近桩底位置(PPT2)处的孔隙水压力变化量小于靠近桩顶位置(PPT1)处的孔隙水压力变化量，这主要是由于土体底部为渗透性较好的砂垫层，而土体顶面为不透水的塑料薄膜。

由图5可知，当桩周土体承受循环温度荷载作用时，可以发现随着循环次数增加，土体中温度引起的超孔隙水压力变化几乎不产生孔隙水压力累积，即孔隙水压力随温度变化可逆。但是，每轮温度循环过程中温度引起的超孔隙水压力变化幅值(单次温度循环过程中最大孔隙水压力与最小孔隙水压力的差值)随循环次数的增加呈现逐渐增大的趋势。这个现象可归因于以下几个原因：1)本文土体为正常固结土，温度升高会会引起正常固结黏土的热固结[31―32]，导致土骨架的强度提高；2)软土的次固结也会造成土骨架强度的提高。综合两个因素影响，土骨架对孔隙水的热膨胀变形的约束作用加强。

(6) 无症状或未识别的心肌梗死。符合下列任一项才能做出诊断:① 有病理性Q波，有或无症状，缺少非缺血病因。② 有与缺血病因相一致的存活心肌丢失的影像证据。③ 有心肌梗死已愈期或愈合期的病理表现。

图4 温度循环引起的桩周土体孔隙水压力变化关系图Fig.4 History of thermally induced pore water pressure of soil surrounding pile

图5 桩周土体孔隙水压力变化幅值图Fig.5 Amplitude change rule of pore water pressure of soil surrounding pile

2.3 桩顶位移变化规律

黏土的次固结会造成桩侧产生负摩阻力，从而造成桩顶沉降[32]。为了消除土体次固结对能量桩沉降的影响，单独进行了1530 min的参照试验，参照试验中桩顶位移随时间变化情况如图6所示。由图6可知，由土体次固结引起的桩顶沉降与对数时间呈线性变化，这个结果与Nguyen等[15]的研究结果一致。需要指出，本文参照试验的持续时间为1530 min (180 min+1350 min)，而能量桩热-力学试验的持续时间为5580 min (180 min+5400 min)。考虑到由土体次固结引起的桩顶沉降与对数时间呈线性变化，本文采用式(2)对 1530 min后次固结引起的桩顶位移进行估算：

式中，St为t时刻的桩顶位移。

图6 参照试验桩顶位移随时间变化曲线Fig.6 Pile head displacement during reference test

热-力学试验和参照试验过程中桩顶位移随时间的变化如图7所示。试验测得的桩顶位移与参照试验得到的桩顶位移相减，可以得到温度荷载引起的能量桩桩顶位移的变化规律。

图7 热-力学试验过程中桩顶位移变化曲线Fig.7 Pile head displacement during thermo-mechanical test

由图7可知，在制热阶段能量桩顶部产生向上位移，在降温阶段桩顶产生向下位移。随着循环次数增加，桩顶产生了不可恢复的累积沉降，且桩顶累积沉降的速率随着循环次数增加逐渐减小。例如，在第一轮温度循环中，能量桩顶部产生了0.7%D的累积沉降；第二轮温度循环中，能量桩产生的累积沉降为0.4%D。20轮温度循环过后，能量桩顶的累积沉降随温度循环次数的变化基本稳定，桩顶累积总沉降为2%D。

桩顶位移与桩体温度之间的关系如图8所示。由图8可知，随着桩体温度升高，桩顶产生向上位移，当桩体温度降低时，桩顶产生向下的位移。且桩顶位移随温度变化率始终小于桩体自由热膨胀曲线，这是由于在桩侧土体的约束作用下，能量桩不能进行自由地膨胀或收缩。

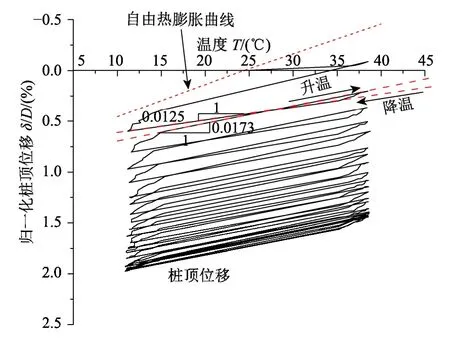
图8 桩顶位移与桩体温度变化关系图Fig.8 Pile head displacement with pile temperature

每轮循环温度荷载作用下能量桩桩顶位移随温度的变化率如图9所示。由图9可知，当能量桩制热时，其桩顶位移变化率始终小于能量桩制冷时桩顶位移变化率，从而导致了能量桩不断产生累积沉降。这是因为当能量桩受热时，由于桩体的热膨胀，桩-土接触面上的法向应力增大，而制冷时恰恰相反。因此，当能量桩制热时，桩体的承载力大于制冷时桩体的承载力，这导致了制冷时能量桩产生更大的位移变化率。随循环次数的增加，制热时能量桩的位移变化率逐渐增大，而制冷时能量桩的位移变化率逐渐减小。当经过 20次温度循环时，制冷过程中和制热过程中能量桩的位移随温度变化率基本相等。因此，此时能量桩桩顶的累积沉降随循环次数增加基本趋于稳定。

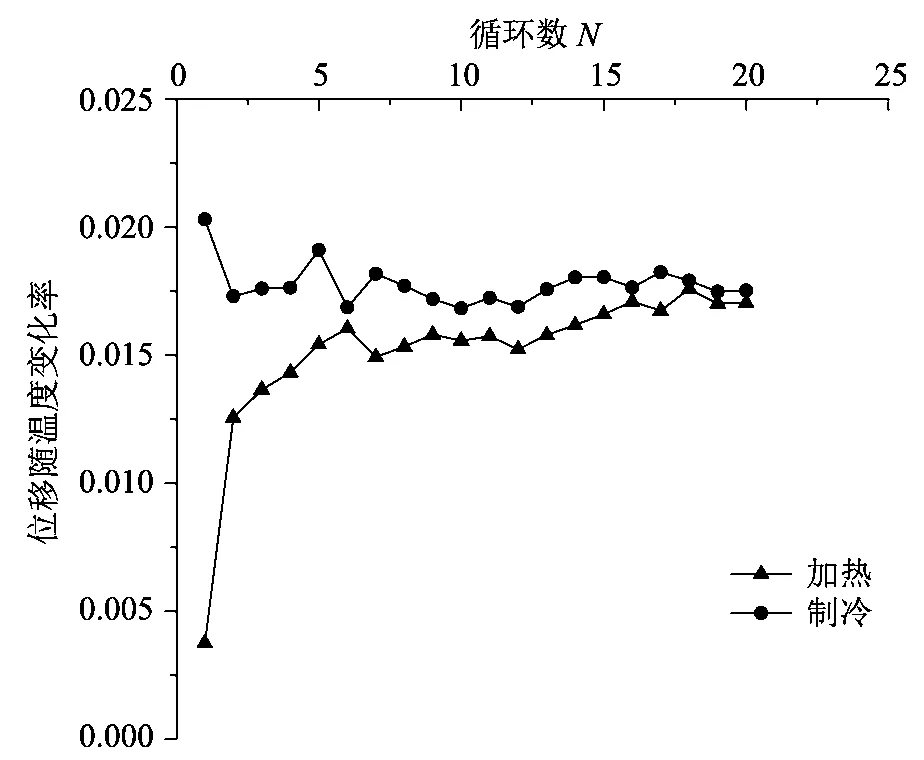
图9 热-力学试验过程中桩顶位移随温度变化率Fig.9 Pile head displacement with temperature during thermo-mechanical test

3 讨论

Ng 等[17]、Stewart和 McCartney[18]开展了循环温度荷载作用下能量桩在饱和黏土、粉土中的离心机模型试验；其中 Ng等[17]试验中为摩擦型桩、Stewart和McCartney[18]试验中为端承型桩，且试验过程中也对桩顶位移进行了观测(如图10所示)。由图10可知，随着温度循环次数增加，摩擦型桩(Ng等[17]和本文试验)的桩顶累积沉降随着循环次数增加而逐渐累积，且逐渐趋于稳定，单次循环所产生的累积沉降随着循环次数增加逐渐减小；端承型能量桩承受循环温度荷载时，桩顶并未发现明显的累积沉降[18]。

图10 前五轮热-力学试验桩顶位移变化曲线Fig.10 Pile head displacement during first five thermo-mechanical cycles

1)当能量桩承受循环温度荷载时，由于能量桩不断地膨胀和收缩，桩-土接触面不断地进行剪切，引起桩-土接触面强度的退化[33―34]，从而导致能量桩产生累积沉降。

2)当黏土的温度升高时，其先期固结压力会随着温度升高而降低，这会导致正常固结黏土产生热固结[16―29]。热固结会加剧桩体上部产生的负摩阻力。

3)能量桩制热和制冷时桩-土接触面上法向应力的不同变化，导致制热和制冷时能量桩桩顶的位移变化率不同(如图9所示)，这也是引起能量桩累积沉降的因素之一。

在实际工程应用中，需要考虑能量桩在长期温度循环荷载作用下产生的累积沉降，否则可能会影响上部结构的安全性和适用性。但是，由于现场条件的多变性以及工程条件的限制，通常无法对长期循环温度荷载作用下能量桩的桩顶沉降进行检测。因此，需要一种能够估算能量桩在长期循环温度作用下产生的累积沉降的计算方法。

本文利用对数曲线，提出利用能量桩在第一次温度循环过程中产生的位移，来预测能量桩承受长期循环温度荷载时产生的桩顶累积沉降变化的经验公式：

式中：Un为第n轮温度循环引起的桩顶位移；N为循环数。

图11 热-力学试验桩顶位移的对数曲线拟合结果Fig.11 Logarithmic curve fiting of pile head displacement during thermo-mechanical test

经过Un=1规一化后能量桩的桩顶位移如图11所示。由图11可知，本文的试验结果能够与经验公式较好的吻合。另外，利用式(3)对Ng等[17]开展离心机试验的结果进行拟合，发现二者也能较好地吻合。这说明利用对数曲线对循环温度荷载作用下能量桩产生的桩顶累积沉降进行拟合是合理的。需要说明，经验公式中存在一个参数α，由于目前开展的黏土中循环温度荷载作用下能量桩力学特性的研究较少，故无法对参数α的影响因素进行分析。因此，需要开展更多黏土中能量桩力学特性的研究以便分析得到参数α的影响因素与取值范围。

4 结论

基于模型试验方法，本文研究了饱和黏土中摩擦型能量桩在长期温度循环过程中的变形特性，可以得到以下几点结论：

(1)桩体及桩周土体的温度随着输入温度的变化而变化；由于土壤热阻的影响，土体的温度变化量小于能量桩的温度变化量，并且距桩中轴线越远，土体温度变化量越小；桩体及桩周土体温度也基本关于环境温度呈现对称变化，且每轮温度循环过程中桩体及桩周土体温度变化规律基本一致。

(2)桩周土体孔隙水压力随着土体温度的升高(或降低)而增大(或减小)，距离桩中轴线越远，土体孔隙水压力变化量越小；随着循环次数增加，土体中温度引起的超孔隙水压力变化几乎不产生孔隙水压力的累积，即孔隙水压力随温度变化变化可逆，但每轮循环过程中温度引起的超孔隙水压力变化幅值随循环次数的增加逐渐增大。

(3)当能量桩制热时，其桩顶位移变化率始终小于能量桩制冷时桩顶位移变化率，从而导致能量桩不断产生累积沉降；且随着循环次数的增加，制热时能量桩的位移变化率逐渐增大，而制冷时能量桩的位移变化率逐渐减小；因此，桩顶累积沉降的率随着循环次数增加逐渐减小；本文试验条件下，当经过 20次温度循环时，制冷过程中和制热过程中桩顶的位移变化率基本相等，此时，能量桩桩顶的累积沉降随循环次数增加基本稳定在 2%D(D为桩径)；可以利用对数曲线对循环温度荷载作用下的能量桩桩顶位移进行拟合。