密集横隔板UHPC箱梁锚固区局部承压性能研究

冯 峥，李传习，潘仁胜，刘科强，聂 洁

(1.长沙理工大学桥梁工程安全控制教育部重点实验室，湖南，长沙 410004；2.佛山市路桥建设有限公司，广东，佛山 528303)

局部承压是土建工程中常见的形式之一，承重结构的支座、预应力结构的锚固区、装配式柱子接头等均系局部承压。关于混凝土局部受压的破坏机理，目前存在两种理论[1]：套箍强化理论[2－3]和楔劈理论[4－5]。刘永颐等[5]在文献[2]的基础上根据实验结果及理论分析进一步提出了混凝土局部承压的楔劈破坏机理，明确了局压底面积的计算办法(同心、对称、有效面积)，导出了 C50及以下标号局压承载力计算公式，为后续高标号混凝土、钢纤维混凝土、超高性能混凝土(UHPC)的局压承载力研究奠定了基础。随着工程技术的发展，C50-C80高强混凝土在工程实践中的逐渐应用，许多学者或相关规范通过混凝土强度影响系数βc计入高标号混凝土抗压强度来减少对局压承载力的影响[6]，通过钢纤维提高系数计入钢纤维对纤维混凝土局压强度的影响[7]。近年来，一些学着开展了UHPC实心截面局压承载力试验[8]和预留孔道活性粉末混凝土局压性能试验[9]，但UHPC局压试验积累的数据依然有限，且均局限于构件层次(棱柱体试件)，对UHPC结构层次的局压试验还极为缺乏。

预应力锚固齿块广泛存在于各类预应力混凝土箱梁桥内，其承载力及抗裂性能关系到结构的安全与耐久性。许多文献对预应力混凝土齿块锚固区(典型的D区)的拉应力分布特征、理解这一特征的典型局部作用的抽象、拉压杆模型构形方法、配筋设计等进行了研究或规定[10－14]。为避免 UHPC箱梁壁厚较小而引起较大的“局部弯曲效应”，其体外预应力锚固可利用密集横隔板的结构优势，采用“隔板连通式齿块”[15]。因隔板的存在，“隔板连通式齿块”锚固区的应力分布特征和力流传递规律与传统齿块锚固区[11－13](包括独立矩形齿块、独立三角齿块、角隅矩形齿块等)明显不同，理解这一应力分布特征所抽象的几种典型局部作用效应及相应的拉压杆模型应有所区别。UHPC相对常规混凝土具有较高抗拉强度和超高韧性[16－18]，锚固区局压承载力如何考虑 UHPC的抗拉强度影响也值得研究。此外，还未见广泛认可的关于UHPC锚固块局压承载力的计算公式。

本文拟通过UHPC薄壁箱梁的体外预应力大吨位张拉试验，验证背景工程中UHPC锚固区的受力是否满足结构正常使用要求，揭示尺寸小巧的“隔板连通式齿块”应力分布规律与受力特性，同时进一步间接积累UHPC局压承载力研究的试验数据。并且通过非线性有限元模型及现有公式对UHPC锚固区进行了承载能力分析。

1 试验模型设计及加载方案

1.1 模型设计

以某拟建UHPC连续梁桥为背景工程进行足尺箱梁模型的大吨位张拉试验。该桥为三跨(56 m+103 m+56 m)变截面 UHPC连续箱梁桥，梁宽16.75 m，预应力筋每束采用19根Φs15.2 mm钢绞线布置，波纹管的孔径为12 cm，锚固体系采用“隔板连通式齿块”。考虑到锚固区受力为典型的局部受力特征[11－13]，根据圣维南原理及有限元受力分析结果，采用背景工程中锚固区的相关尺寸制作一片带锚固区的足尺UHPC小箱梁节段模型。试验小箱梁顶板厚 220 mm，腹板厚 180 mm，横隔板厚120 mm，横肋板厚200 mm，横隔板与横肋间距相隔 1.5 m。沿纵桥向方向分两部分浇筑，锚固区部分为2140 mm长的UHPC梁段，为便于施加张拉荷载在 UHPC梁段的非齿块侧浇筑 700 mm厚的C50混凝土梁段。锚固(齿)块为三角形齿块，锚固在横隔板和横肋上，齿块端面高470 mm、宽400 mm。为提供足够大的张拉荷载，纵向预应力筋采用 25根直径为15.2 mm、标准强度为1860 MPa的成品索。波纹管的孔径Dduct为155 mm，锚垫板的直径Da为310 mm，锚垫板的长度Ha为270 mm。螺旋筋采用直径为 16 mm 的普通钢筋(屈服强度fy=235 MPa)，中径Dsp为 280 mm，螺间距psp为60 mm。试验箱梁的详细设计尺寸如图1所示。

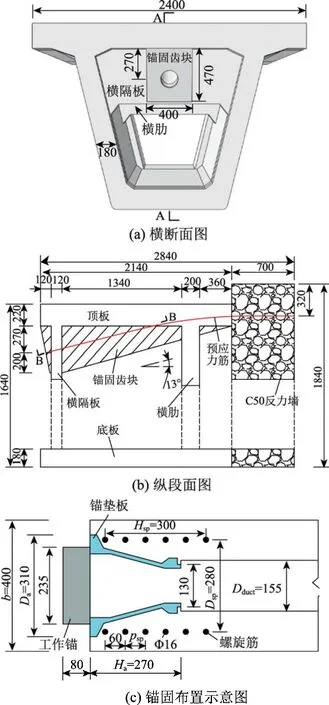
图1 试验模型设计尺寸图 /mmFig.1 Dimensional design of the test model

试验梁中 UHPC梁段配筋采用 2种直径的钢筋，均为HRB400型普通钢筋，钢筋布置情况如图2、图3所示。其中，图2为锚固块以及与其相连的顶板处配筋情况，钢筋直径为16 mm；图3为横隔板部位的钢筋布置情况，钢筋直径为12 mm；非关注部位或配筋对其受力分析影响不大的部位(包含横肋、底板、腹板等)的钢筋布置情况图中未给出。

试验梁中UHPC材料来自于长沙理工大学研发的UHPC拌和料[19]，钢纤维采用直径13 mm长的平直形纤维，体积掺量为2.5%。UHPC拌和料共分4盘浇筑，每盘浇筑0.875 m3，共计3.5 m3。取拌合料制作抗压试件(100 mm×100 mm×100 mm)、抗折试件(100 mm×100 mm×400 mm)、轴压试件(100 mm× 100 mm×300 mm)、弹性模量试件(100 mm× 100 mm× 300 mm)各三个，并与试验梁一同蒸汽养护后进行材性试验。试验梁实测的平均抗压强度为163.0 MPa，平均抗折强度为27.9 MPa，平均轴压强度为142.7 MPa，平均弹性模量为44.0 GPa，与小批量浇筑试验结果基本一致。

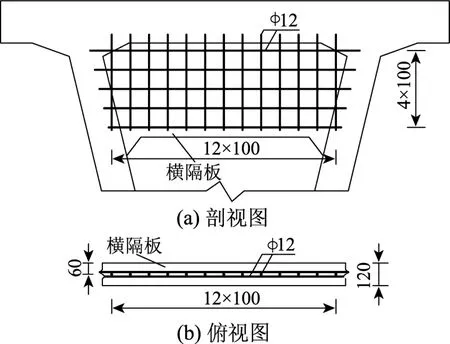
图3 横隔板钢筋布置图 /mmFig.3 Layout of steel bars in diaphragm

1.2 试验测点布置

在锚固齿块内部钢筋以及梁段表面的关注位置布设应变片，钢筋部位应变片(尺寸2 mm×3 mm)测点布置参见图4(编号为 R1~R5，沿钢筋方向布置)。UHPC梁段应变片布设在锚固区顶板、横隔板、横肋及齿块侧表面上，均采用5 cm长的电阻应变片，布置情况参见图4、图5。其中I1位于锚固齿块的侧表面，布置方向与齿块底边纵向平行；I2~I5位于齿块中轴线位置，各测点间距相隔300 mm，布置方向与齿块底边纵向平行，I13~I15位于横肋部位。I10与I9、B6与B1关于箱梁纵向中心线对称。其他各点布置情况可通过布设图较易获知，不再赘述。

图4 锚固齿块应变片布置情况Fig.4 The layout of strain gauges in the anchor block

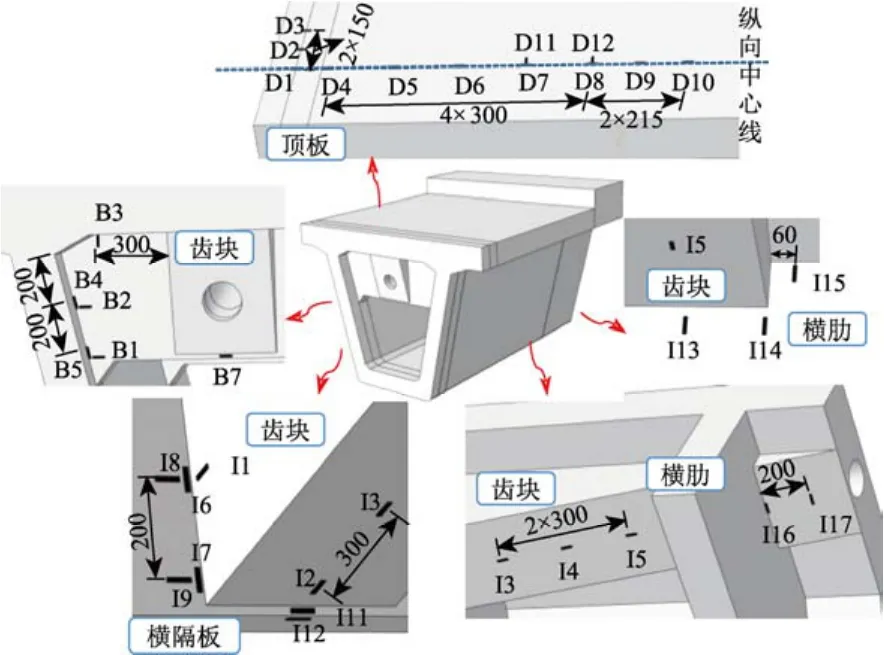
图5 UHPC箱梁混凝土应变片布置情况 /mmFig.5 The layout of strain gauges on the UHPC box-girder

1.3 试验加载方案

张拉控制荷载取为 4700 kN(钢绞线控制应力的 72%)，分 13级进行加载。加载历程为 0 kN→282 kN→0 kN→282 kN→979 kN→2453 kN→3228 kN→3382 kN→…→4546 kN→4700 kN。

为保证试验中的人员、设备安全，采用了Kim等[20]提出的 UHPC锚固块承载能力计算公式进行试算，参见式(1)：

式中：A为锚固齿块端面的面积；为锚垫板的面积；为锚垫板的有效面积；为预应力孔道的截面面积；和As分别为螺旋筋的屈服强度和截面面积；K(n)=。

根据式(1)及锚固齿块的相关尺寸可初步预测UHPC锚固齿块的局压承载力Fu=10779.0 kN，其值是试验梁实际张拉荷载4700 kN的2.3倍，因此试验中具备足够的安全富余度。

试验梁通过 25根钢绞线提供张拉力，钢绞线一端与齿块相连，另一端与C50反力墙相连。张拉荷载在加载到指定荷载后持荷 5 min，保证力流传递稳定，并每次测量三组数据，尽量消除突加荷载对数据的影响。试验梁张拉现场情况参见图6。应变数据用静态应变数据采集仪TDS105采集，采用裂缝观测仪ZBL-F800观测锚固区的开裂情况。

图6 试验箱梁张拉试验现场Fig.6 The tension test siteof the test box-girder

2 有限元分析

2.1 非线性有限元模型

利用 ABAQUS建立有限元模型(FEM)对试验梁进行非线性全过程的受力分析，如图7所示。采用混凝土塑性损伤模型(CDP)模拟试验梁的局压受力情况[20－21]。梁体部分采用实体单元C3D8R模拟，UHPC弹性模量E按试验值取44.0 GPa，泊松比v取0.2，CDP模型所采纳的UHPC拉压本构模型在2.2节专门论述。C50反力墙非试验中关注部位，为便于计算采用理想线弹性模型模拟，弹性模量E取34.5 GPa，泊松比v取0.2。试验梁内钢筋采用T3D2单元模拟，并按两阶段理想弹塑性材料考虑，其中普通钢筋弹性模量E取200 GPa，螺旋钢筋弹性模量E取210 GPa，泊松比v均取0.3。FEM假定钢筋与UHPC梁段粘结无滑移，采用Embedded命令使钢筋与梁段共同受力。边界条件为约束梁底面的竖向自由度以及反力墙底面的x、y、z三个方向的自由度。张拉荷载值均分阶段施加于FEM。关注部位的网格细化为15 mm，非关注部位网格划分较为粗糙，单元总数为654544个，节点总数为786366个，计算结果收敛良好。

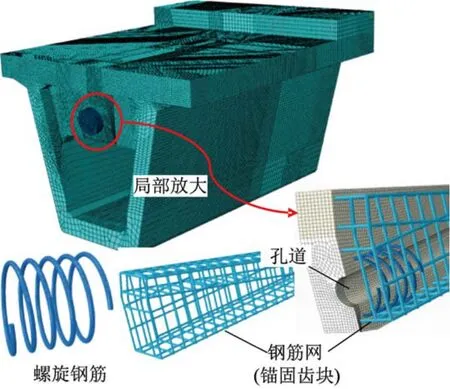
图7 有限元模型Fig.7 Finite element model

2.2 UHPC拉压本构关系

在 FEM 分析中，UHPC轴压本构取自文献[22―23]中的本构模型，如式(2)所示：

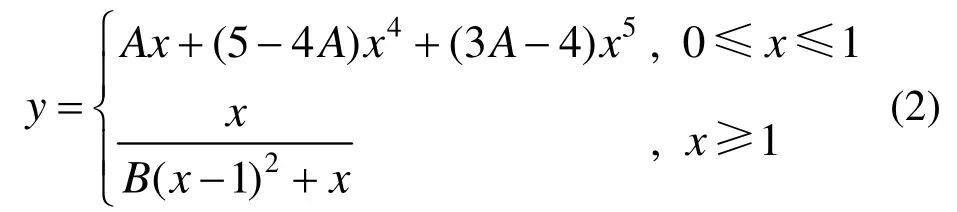
根据UHPC材料的轴拉实验结果，试验梁采用的UHPC满足应变硬化材料的特征。UHPC两阶段拉伸本构模型如图8所示(图中wpc为应变软化阶段起始点的裂缝宽度)。研究结果[17―18,24]表明 UHPC弹性及应变硬化阶段的本构关系如公式(3)所示。

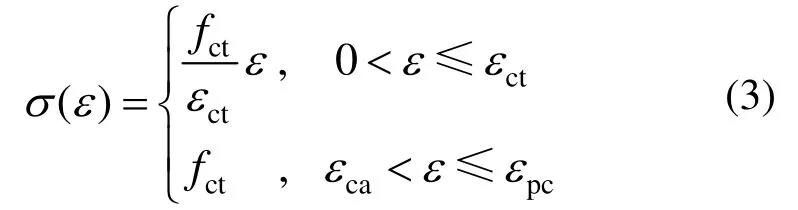
由于应力-裂纹宽度关系无法直接用于CDP模型，FEM中 UHPC应变软化阶段的本构模型根据文献[16]提出的应力-裂纹宽度公式、法国规范[24]以及文献[25]中方法转变而来的应力-应变关系取值，参见式(4)：

式(3)、式(4)中：fct为应变硬化阶段的平均应力(取自实验值8.35 MPa)；ε为拉应变值；εct为弹性阶段的峰值应变(取实验值 197 με)；εpc为极限拉伸应变(取实验值 1317 με)。

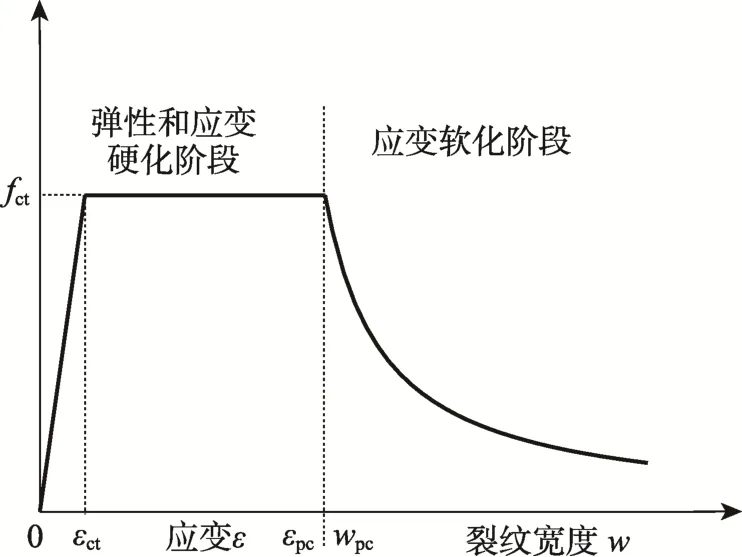
图8 UHPC两阶段拉伸本构模型Fig.8 Two-stage tensile constitutive model of UHPC

2.3 锚固区应力分析

由于试验模型未考虑锚后牵拉效应，因此在原有限元模型的基础上将四周壁板的长度往梁端延长40 cm，建模方法与上述方法基本一致，不再赘述。根据FEA结果，试验梁拉应力较大部位主要分布于下述5个区域(参见图9)：1)位于锚后顶板下表面以及齿块与顶板交接区域，“锚后牵拉效应”和“悬臂效应”[11,14]较为显著；2)位于横隔板内侧面与齿块交接区域(表现为横隔板内侧面与齿块交接区域的横桥向与竖桥向的拉应力集中)，该处处于力流扰动及几何突变区，应力梯度值较大，“隔板弯曲效应”较为显著，这是由于张拉过程中齿块带动横隔板产生沿纵桥向的位移，而腹板对横隔板的约束相当于固结约束，在横隔板内侧面与齿块交接区域产生了弯矩；3)位于横肋与齿块交接区域，该处虽位于钢束转向区，但由于横肋提供了支承作用且尺寸较为厚实，该部位的最大拉应变较小，仍处于弹性阶段，“径向力效应”较不显著；4)位于横隔板与横肋之间的顶板区域，该部位虽可见明显的“局部弯曲效应”，但该区域UHPC的应变值未进入到应变硬化阶段，由此亦说明横隔板与横肋的锚固作用大大减小了锚固区的“局部弯曲效应”；5)位于齿块锚下部位，力流沿横向传递且应变值较大，“锚下劈裂效应”较为显著。

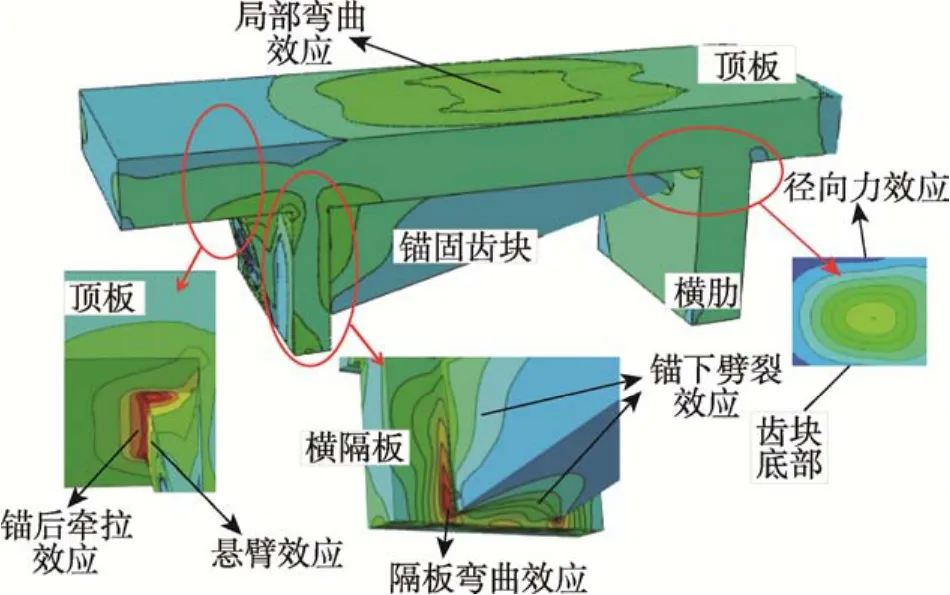
图9 “隔板连通式齿块”典型局部作用效应Fig.9 The typical local effect of the DABIAS

锚固区为典型的应力扰动区[11－13]，其局部作用效应分析仅能得到应力集中分布区域，但无法判断锚固区的破坏模式。文献[26]开展了UHPC块体预留贯通圆形孔道的局压试验，试验结果表明局压试件为先裂后坏的破坏模式，主要表现为楔形体对核心母体和外围母体的劈裂破坏；该实验采用长×宽×高为200 mm×200 mm×400 mm的棱柱体试件，试验中UHPC材料抗压强度为120.5 MPa，抗拉强度为8.6 MPa，弹性模量为33.59 GPa。根据其试验模型及试验结果开展了有限元分析，原试验结果与本文FEA劈裂应力计算结果参见表1。

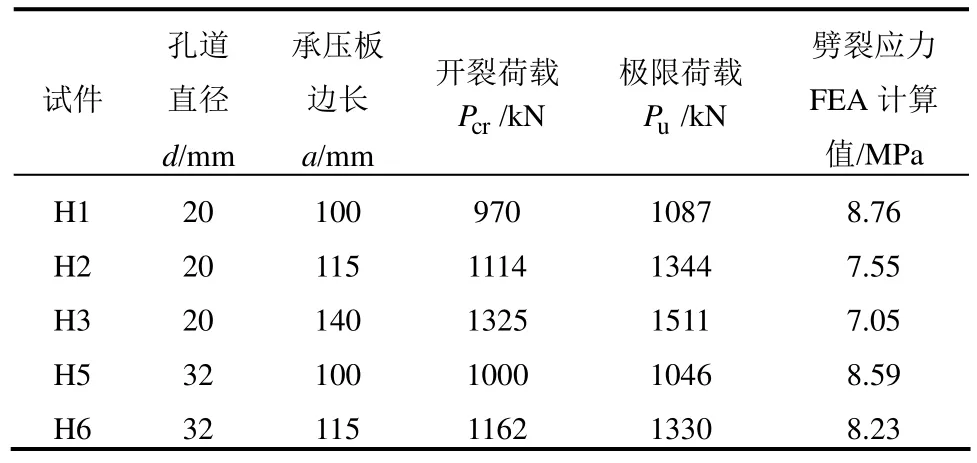
表1 棱柱体局压试验及其劈裂应力有限元计算值Table 1 The local compressive test and its FEA value of splitting stress

根据表1可知，各试件开裂时的劈裂应力与UHPC的直接拉伸强度8.6 MPa较为接近，因此锚固区的劈裂破坏为受拉破坏(楔劈理论[4－5])。

根据锚固区力流传递方向及受力模式(图9、图10)，“锚后牵拉效应”、“径向力效应”以及“悬臂效应”力流方向与受力方向一致，具有明显的直接拉伸特征。顶板部位主要承受弯矩作用，虽受力模式与直接拉伸的受力模式略有不同，但UHPC梁的弯曲破坏试验[25]、四点弯曲实验以及法国规范[24]均表明，弯矩作用下的受拉开裂由拉应力控制。“隔板弯曲效应”是在预应力荷载的作用下引起的横隔板局部弯曲，在受力模式上与“局部弯曲效应”一致。

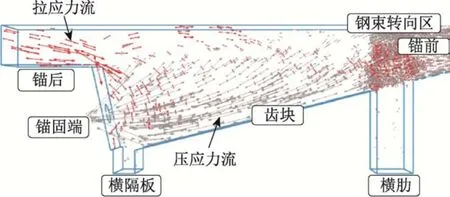
图10 锚固区应力迹线分布图Fig.10 Distribution of stress trace for the anchorage zone

综上所述，齿块锚固区虽为应力扰动区，但可根据所得应力值结合 UHPC的轴拉应力-应变曲线对锚固区的开裂、受力状态进行初步的判断。而UHPC轴拉本构曲线有较长的应变硬化段(图8)，应变随着荷载的增加而增加但应力基本保持不变，因此齿块锚固区在局压荷载作用下的实际受力情况可根据轴拉应变值进行初步判断。

3 试验结果与分析

3.1 试验梁开裂情况分析

试验中UHPC梁张拉到4700 kN时未发现可视裂纹(采用裂缝宽度达到 0.05 mm作为可视初裂的标准[16])，锚固块内的钢筋亦未屈服(见图11)，因此UHPC箱梁“隔板连通式齿块”满足实际工程中的正常使用要求。

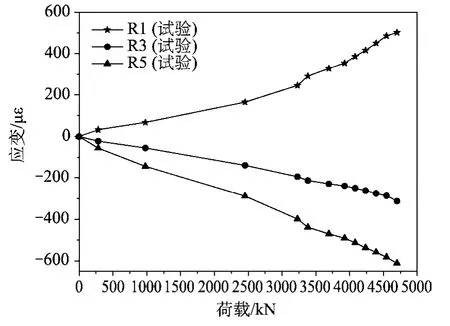
图11 钢筋处荷载-应变曲线Fig.11 The load-strain curves of the steel bars

单就张拉荷载进行比较，背景工程中 19根钢绞线设计方案齿块锚固区至少有31.6%的承载力强度富余。根据文献[26]的研究成果，增大预应力管道孔径会削弱锚固区的承载能力，试验梁孔径相对于原设计增加了29.2%，试验梁(25根钢绞线)相对于背景工程实桥设计(19根钢绞线)局压承载力降低了23.6%，因此原设计中UHPC锚固区远不止31.6%的承载力强度富余。综上所述，图1所述钢束锚固体系完全能满足实际工程的受力要求。

3.2 锚固区局部作用效应分析

根据箱梁顶板部位关注点的荷载-应变曲线(图12)可知，试验结果与FEA结果吻合较好，应变差值小于20%。当张拉荷载逐渐增大时，顶板部位各测点应变值基本成线性变化；顶板处纵桥向拉应变值较小，而横桥向的D11、D12测点最大拉应变达到201 με，略微超出UHPC弹性峰值应变197 με，“局部弯曲效应”较不显著。此外，箱梁顶板处拉应力分布特征为：沿试验梁纵桥向拉应力值逐渐减小，在靠近反力墙的位置逐渐转变为压应力。

图12 箱梁顶板关注点荷载-应变曲线Fig.12 Load-strain curves of the top slab

由锚固处钢筋的应变情况可知(图11)，在4700 kN的最大张拉荷载作用下钢筋处最大拉伸应变达到了502 με，位于R1测点处，“锚下劈裂效应”较为显著。

由图13(a)可知，沿钢束方向齿块主要承受压应力，随张拉荷载增加，齿块部位各测点压应变值为线性增长变化，最大压应变位于靠近齿块端部的I3测点(-860 με)，无压碎破坏的风险。根据齿块压应变分布特征可知，I3测点位于核心受压区，即沿齿块钢束张拉方向压应变值先增大后减少，在I3测点位置达到最大值。此外，由图13(b)可知横肋部位的应变值均较小，最大实测应变值不足150 με，UHPC材料仍处于弹性阶段，而钢束转向产生的拉应变达到了205 με(位于I16)，但无开裂风险。因此，钢束转向产生的“径向力效应”对锚固区的承载能力基本无影响，与有限元分析结果一致。

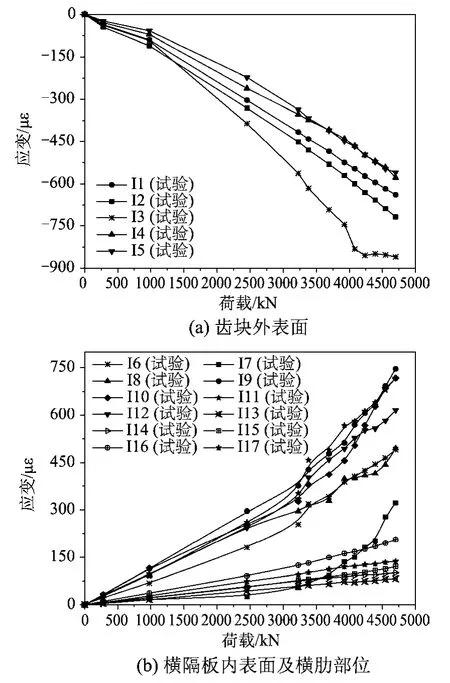
图13 箱梁内腔关注点荷载-应变曲线Fig.13 The load-strain curves of the inner chamber of the box-girder

加载前期横隔板部位各测点应变值随荷载增加基本为线性关系(见图13(b)、图14)，但当荷载张拉到 3382 kN时，应变进入到线性偏离阶段，之后应变值随张拉荷载的增加而非线性增加。当达到最大张拉荷载 4700 kN时，其最大拉应变达到了746 με，由此表明“隔板弯曲效应”较为突出。

基于以上分析，UHPC箱梁“隔板连通式齿块”锚固区的“锚下劈裂效应”和“隔板弯曲效应”在设计中应引起重视。此外，由试验结果可知，虽然箱梁模型中UHPC材料在大吨位张拉荷载的作用下进入到应变硬化阶段，但锚固区并未开裂。因此，在设计中可适当考虑UHPC的拉伸应变硬化特征。

图14 箱梁横隔板外表面关注点荷载-应变曲线Fig.14 The load-strain curves of the outer surfaceof diaphragm in the box-girder

4 锚固区局压承载能力分析

4.1 锚固区局压承载力结果

由于试验模型未加载至破坏，为得到锚固块的局压承载能力，对上述非线性有限元模型增大试验力处理，直到加载至锚固块“开裂失效”(以荷载-位移曲线的峰值点作为判别承载失效的标准)。据UHPC锚固区试验结果及有限元分析结果可知，“锚下劈裂效应”是导致锚固齿块局压破坏的主要因素之一，其锚下劈裂区域的应变值随荷载增大的变化情况如图15所示。

图15 “锚下劈裂效应”荷载-应变曲线Fig.15 The load-strain curves of the bursting-force effect

当荷载加至6640.7 kN时，锚固区应变值开始进入到应变软化阶段，该区域的UHPC逐渐退出工作。由锚固区加载点的荷载位移曲线可知(见图16)，随着荷载的继续增加，UHPC锚固区的塑性损伤程度急剧增加，观测点的位移随之快速增加，最终局压承载力达到9958.7 kN时UHPC锚固块“开裂失效”。

4.2 UHPC局压承载能力计算分析

为得到适用的UHPC锚固块的局压承载力计算公式，根据图1齿块尺寸及已有文献资料[7,20,27－30]进行局压承载力计算分析，计算结果参见表2。限于篇幅，不再对各计算公式进行详细解释说明，具体请参见各文献。

图16 加载点荷载-位移曲线Fig.16 The load-deflection curves of the loading point.

由表2可知，根据不同文献及规范所得的计算结果差距较大，最大差值达到了40.9%(文献[20]与文献[30])。这是由于公式中的相关系数取值存在较大的差异所致，例如《公路超高性能混凝土(UHPC)桥梁技术规程》(征求意见稿)[30]中混凝土局部承压修正系数ηs(即规范[7,27]中混凝土强度影响系数βc)取 0.54、间接钢筋影响系数k取1.125，而《超高性能混凝土结构设计技术规程》(征求意见稿)[29]中混凝土局部承压修正系数的取值接近 0.8、间接钢筋影响系数k取 2.2，导致其计算结果亦相差了32.2%。由此说明目前关于UHPC局压承载力的计算公式还未形成共识，还需继续开展广泛而深入的研究。与文中FEA计算结果的对比情况而言，文献[20]以及规范[27,29]的预测结果较为精确，计算差值不超过10%，其局压承载力计算公式[20,27,29]可供工程中参考应用。

此外，根据AASHTO设计指南(2017)[31]，锚固装置的承载力计算可按进行计算，其中φ为混凝土抗力系数(对于后张预应力混凝土结构φ一般取1)。因此根据Kim公式的计算结果及 AASHTO设计指南(2017)[31]中建议公式对 Kim方程进行改进，改进后如式(5)所示：

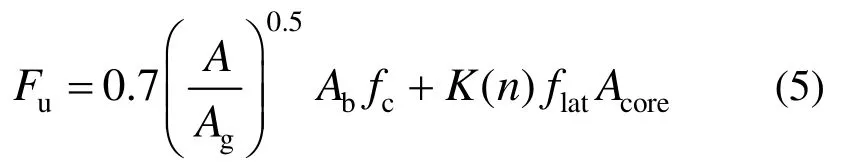
由式(5)可得 UHPC锚固区的局压承载力为9603.6 kN，为FEA计算结果(9958.7 kN)的0.964倍，具有较好的计算精度。

表2 UHPC锚固区局压承载力计算值Table 2 The calculated values of local compressive bearing capacity for the UHPC anchorage zone

5 结论

通过大吨位张拉试验及非线性有限元方法对UHPC箱梁“隔板连通式齿块”锚固区进行了局压性能研究，得到了以下结论：

(1)UHPC锚固区开裂为拉应力控制，考虑到UHPC材料的应变硬化特征，其开裂风险可根据UHPC的拉伸应变值进行初步定性判断。

(2)UHPC箱梁“隔板连通式齿块”中“局部弯曲效应”和“径向力效应”均不显著，但应对“锚下劈裂效应”和“隔板弯曲效应”引起重视，这两种效应是导致“隔板连通式齿块”承载失效的重要因素。

(3)背景工程中尺寸小巧的“隔板连通式齿块”锚固体系张拉到4700 kN时无开裂风险，采用19根钢绞线的常规锚固设计，锚固区有较大的承载力强度富余，采用 25根钢绞线锚固亦能满足结构正常使用要求，可在工程中广泛采纳。

(4)UHPC箱梁锚固区中拉应力值即便进入到了拉伸应变硬化阶段结构仍能正常使用，在设计中可适当利用UHPC的拉伸应变硬化特征，进而减少钢筋等材料用量。

(5)基于已有文献及规范的局压承载力计算公式的计算结果差距较大，最大差值达到了40.9%。

而基于Kim公式、《活性粉末混凝土结构技术规程》以及《超高性能混凝土结构设计技术规程》(征求意见稿)中局压承载力计算公式所得结果较为接近。