基于CPU/GPU异构系统架构的高超声速湍流直接数值模拟研究

党冠麟，刘世伟，胡晓东，张鉴，李新亮

1.中国科学院力学研究所，北京 100190

2.中国科学院计算机网络信息中心，北京 100190

3.中国科学院数学与系统科学研究院，北京 1 00190

4.中国科学院大学，北京 100049

引言

湍流是常见的自然现象，自然界的流动多以湍流形式呈现。人们对湍流的系统性研究始于上世纪20年代。经过百年的发展，现今人们对一些湍流现象已经可以较好地进行描述和预测，但过往大多数湍流研究结论都还是经验性的，对湍流的基础性理解依然欠缺。2000年，美国克雷（Clay Mathematics Institute，CMI）数学研究所悬赏了七个重要的数学难题，N-S方程（Navier-Stokes方程，流动控制方程）的求解位列第六。深入研究湍流，可以加强人们对随机性和确定性的认识。

在工程方面，受航空航天等领域需求的引导，高超声速湍流（一般指来流马赫数大于5）成为当前流体力学研究的热点。飞行器表面流体从层流转捩到湍流后，摩阻和热流变为原来的数倍。理解湍流与转捩的机理，对解决运载火箭导弹热防护、大型飞机减阻降噪、吸气式高超声速飞行器发动机燃烧室湍流混合等问题有重要意义。

直接数值模拟（Direct Numerical Simulation,DNS）是研究湍流的重要手段。DNS是使用足够密的网格直接离散求解N-S方程，可以识别最小尺度的湍流涡，能够得到湍流与转捩过程时空间演化的全部信息，是目前最为可靠的湍流计算手段。精细的DNS 不仅可以帮助人们对湍流机理开展研究，也能为飞行器等工程装备设计提供参考与评估，甚至可以发现实验中难以观察到的现象，扩展人类认知的边界。高超声速湍流DNS 开展较晚，近十余年才发展起来，主要原因之一是湍流DNS 对空间网格规模与时间推进步数的要求极高，计算量极大，根据Lesieur M的推算，在积分尺度为L的实际问题中，对应雷诺数为ReL，则 DNS所需的空间网格数和时间步数至少要达到O(ReL9/4)和O(ReL1/2)[1]。美国Boeing 公司的Edward N.Tinoco 在2009年估计，以当时的计算机发展速度，到2080年才有可能对民航客机全机进行DNS[2]。

在过往对高超声速湍流的DNS中，往往通过在大规模CPU集群上做并行计算来实现，节点间采用MPI（Message Passing Interface）、ZeroMQ（0MQ）、Hadoop 等方式进行数据通讯。然而，多核架构的CPU的计算能力现今已被众核架构的GPU甩在身后，图1、图2分别展示了2003年以来Nvidia GPU与Intel CPU的单、双精度浮点运算峰值性能和访存带宽的对比，可以看出，GPU的峰值性能与访存带宽如今都已经达到CPU的近百倍。表1展示了2019年11月公布的超级计算TOP500榜单前十位，其中一半超算采用了异构加速器的模式，说明利用GPU等加速器进行加速计算的异构模式已经成为高性能计算发展的主流。

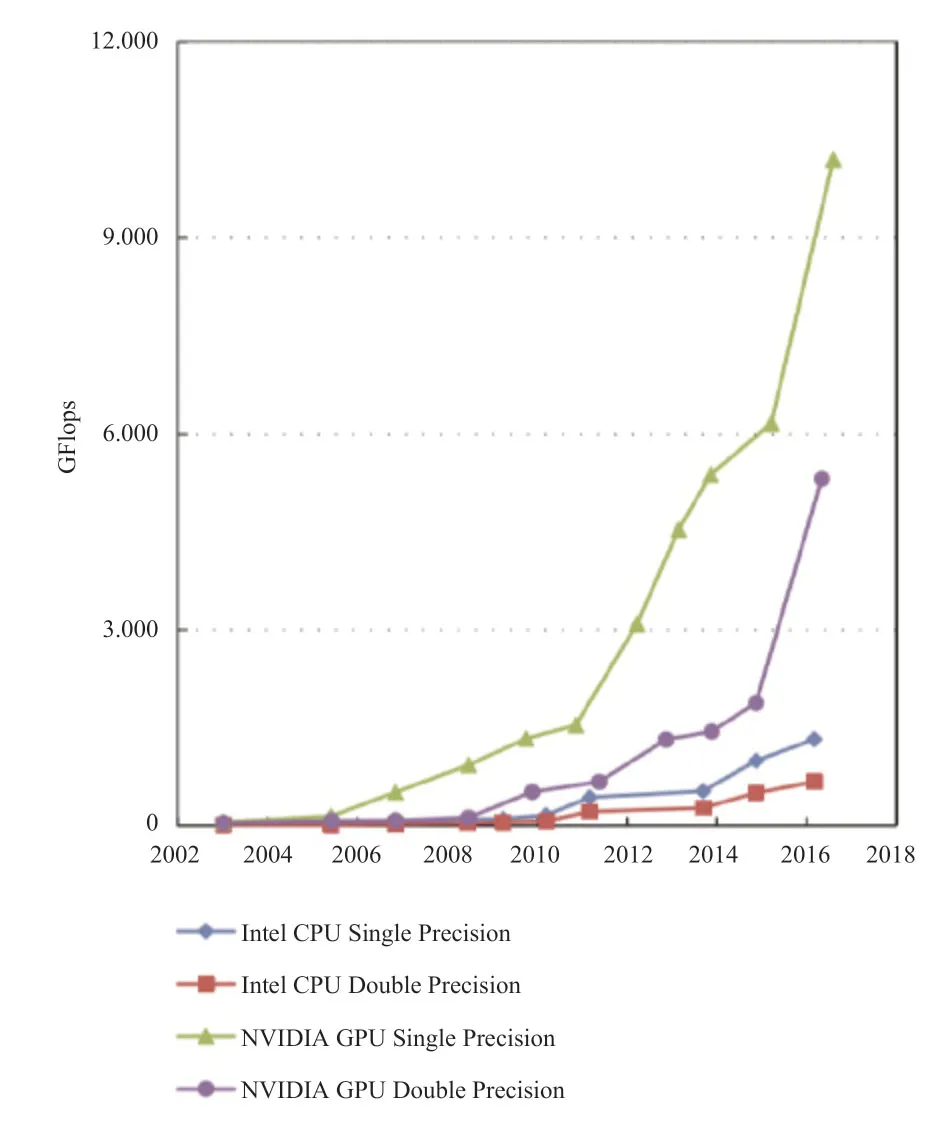
图1 CPU与GPU浮点运算能力[16]Fig.1 Floating-point operations per second for CPUand GPU[16]

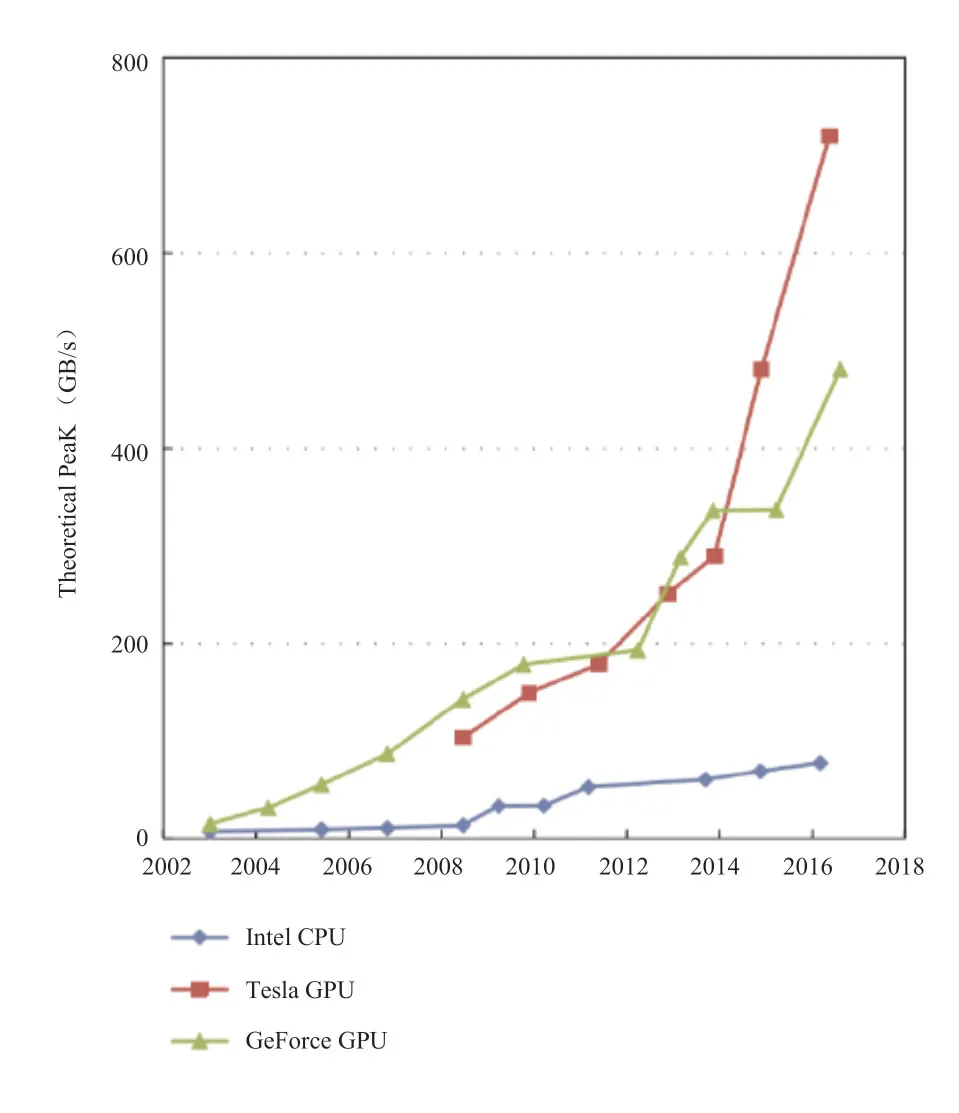
图2 CPU与GPU的带宽[16]Fig.2 Memory bandwidth for the CPUand GPU[16]

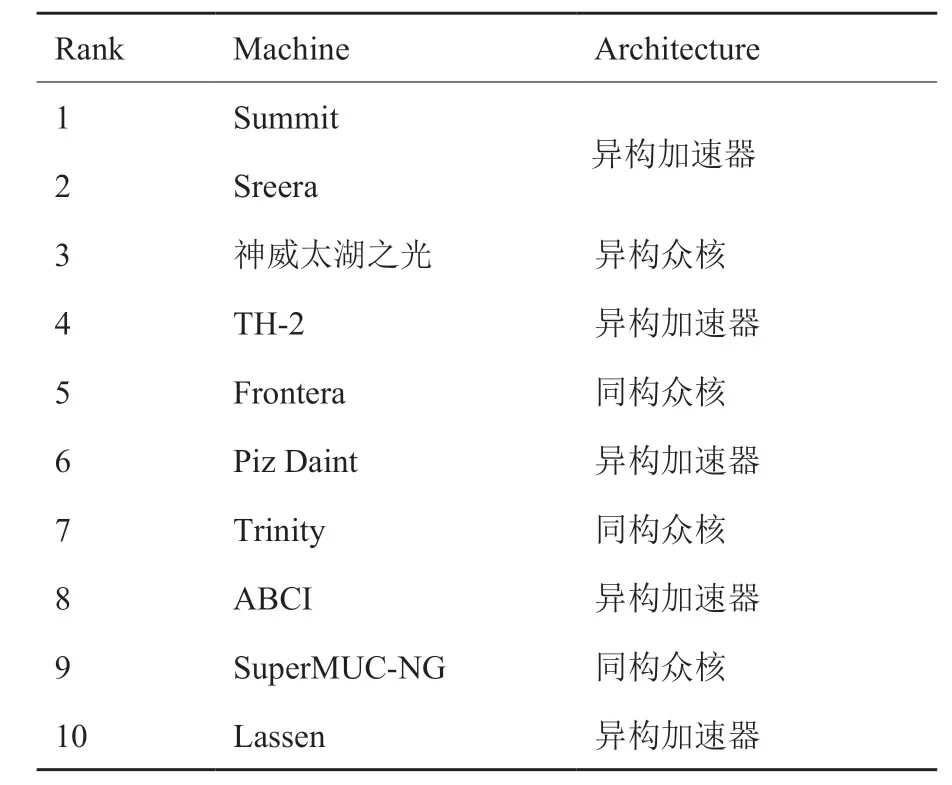
表1 超级计算TOP500榜单中前十名[17]Table1 Top 10 in the TOP500Supercomputer list[17]

利用GPU求解流体力学问题前人已经开展过一些工作，2003年Takashi Amada 在GPU上实现了基于平滑分子动力学（Smoothed Particle Hydrody-namics）的粒子流动模拟[3]，同年，J.Kruger 利用GPU求解了二维不可压N-S方程[4]。2007年，T.Brandvik 完成了二维Euler方程在GPU上的求解[5]，随后他将求解器扩展到了三维[6]。2010年，D.Jacobsen 利用MPICUDA 在128个GPU上并行求解了不可压N-S方程，但弱扩展性只有17%[7-8]。随后他将GPU并行数量扩展到256，三维并行效率依然没有提高[9]。2012年，Khajeh-Saeed 使用192块GPU对均匀各项同性湍流进行了DNS[10]。2014年，Wang 利用GPU对壁湍流分别进行了LES和DNS，他的工作是基于求解LBE（Lattice Boltzmann Equation）[11]。2015年V.Emelyanov开发了基于GPU的三维可压缩的欧拉方程与N-S方程有限体积法求解器，获得20到50倍的加速[12]，之后他们对亚、跨、超声速翼型外流场利用GPU开展了数值模拟，最高马赫数为1.6[13]。2018年，Lai 等人利用CPU/GPU异构系统架构下的可压缩NS方程求解器，对高超声速的双椭球绕流进行了计算，马赫数为8.02[14]。随后，他们又开展了对最大马赫数为10.02的高超声速三维航天飞机模型的数值模拟，在4块GPU上取得了比单块CPU最大147倍的加速效果[15]。

本文利用GPU对高超声速湍流问题进行DNS，最大扩展到64块GPU卡，证明GPU可以用于高超声速湍流DNS，并能大大缩短计算时间。

1 控制方程与数值方法

1.1 控制方程

本文使用的有限差分法求解器基于三维可压缩N-S方程。形式如下：

其中U为守恒变量，包含质量密度、动量密度与能量密度，F1，F2，F3为三个方向的无粘通量，G1，G2，G3为三个方向的粘性通量。

其中粘性通量中的粘性应力由牛顿应力方程获得。总能E 由内能与动能组成。为使方程封闭补充，另需补充理想气体状态方程。

计算基于无量纲的N-S方程。

在计算时，利用三维Jacobian 变换，将物理空间的网格变换到直角坐标系下的计算空间后进行计算。

1.2 空间离散格式

为减少无粘项的混淆误差，保证计算稳定，无粘项先使用Steger-Warming 分裂[18]，后利用7 阶Weno-SYMBO[19]格式离散。Weno-SYMBO 格式相比于传统Weno 格式，在保持高精度的同时，具有更小的数值耗散，更利于计算湍流问题。

粘性项使用6 阶中心格式进行离散。

1.3 时间推进格式

湍流问题具有极强的非定常性，为能够分辨出湍流结构实时变化，时间步长不能取得太大。显式格式计算量小，物理问题所必须的较小时间步长正好保证了计算稳定性，非常适合湍流计算。此处使用TVD 型的三步三阶Runge-Kutta 方法。

1.4 滤波

高超声速问题由于流场动能非常接近于总能，计算如果产生非物理波很可能使动能超过总能，进而出现负温度导致的计算发散，为增加计算稳定性，在计算过程中，每经过10 步计算进行一次滤波，以滤除流场中高频非物理波。守恒型滤波色散误差小，对计算结果影响较小。这里采用守恒型的捕捉激波滤波[19]。

2 Opencfd-SCU程序流程与GPU程序特点

CPU/GPU异构系统架构（HSA）下的计算流体力学程序OpenCFD-SCU（OpenCFD Scientific Computing - CUDA）以作者前期开发的高精度有限差分求解器OpenCFD-SC[20]为基础，两者使用相同的程序框架，程序框架如图3。

图3 OpenCFD-SC 计算流程Fig.3 The program hierarchy of OpenCFD-SC

程序先读入控制文件中的参数信息，并通过MPI_bcast 广播到各个进程，之后，各个进程读取初值与网格，并使用Memcpy3D 将初值与网格信息传递到GPU的全局内存（Global Memory），而后，利用GPU计算Jocabian 系数。程序初始化完成，正式进入计算环节。

程序的所有计算都在GPU上进行，为了避免过多的CPU-GPU间数据传输影响程序性能，数据在传递到GPU上之后，全程储存在GPU的全局内存中，CPU-GPU间数据通讯只在需要进行数据交换时启动。

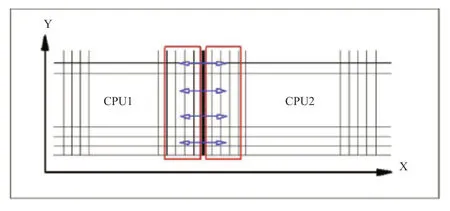
图4 区域分割示意图Fig.4 Sketch map of region segmentation

为最大化减少数据交换量，以提高并行效率，我们只对差分需要的边界上3-4 层数据进行交换。如图4所示，以二维为例，只有MPI 进程之间差分计算涉及的重叠部分网格点上的数据需要进行数据交换。交换时。需要交换的数据要先从GPU传递到CPU，然后，CPU之间通过MPI 进行数据交换，最后，CPU将交换得到的数据再传至GPU，GPU继续接下来的计算。CPU上的MPI 分割采用三维剖分。目前为了保证计算的稳定，采用阻塞式通讯。

程序中所有数据都是双精度。

3 Opencfd-SCU程序优化

GPU程序编程思想与CPU程序不同，GPU编程实际是控制线程索引与数据地址指针的关系，从而操作成大量线程同时对数据进行计算。GPU上的资源类型较复杂，在GPU上进行程序优化，主要以最大化利用GPU资源为思想。以下是我们做的一些工作。

3.1 数据重排列

在进行CPU-GPU间数据交换时，我们在GPU上将所有需要交换的数据重排列为连续一维数组，再通过Memcpy 传递至CPU。

之所以进行重排列操作，是因为需要传输的数据是数据块边界上的数据，只是完整数据块中靠外的几层，他们在全局内存中的存储并不连续，而GPU较高的访存带宽是通过高访存位宽实现的，只有对在内存中连续排列的大数据块，GPU高访存的特性才能充分发挥，在计算时，可以通过对内存进行对齐与合并，再控制指针访问内存中的数据，从而降低数据内存不连续带来的影响。然而，在使用Memcpy函数拷贝数据时，函数默认的访存与传输方式难以控制，不连续的数据对Memcpy 函数效率影响明显，直接影响了CPU-GPU间数据传递速度。在我们的测试中，重排列的操作可以明显提升Memcpy 速度。

3.2 对块的大小进行控制

GPU的线程层次由线程格、线程块、线程（Grid，Block，Thread）三层组成，每层又可以构成一个x，y，z方向的三维结构。

而GPU程序运行时，可以理解为数据被划分为许许多多的数据单元，由流式多处理器（Streaming Multiprocessor，SM）控制线程对各个数据单元进行操作。SM是GPU上重要的共享资源，每个GPU上SM 数量固定，Nvidia Tesla V100为80个，最大化SM 占用率，才能最大化GPU性能。

SM通过控制线程束（Warp）来操作线程的行为，线程束是线程调度的最小单位。实际上，GPU对每个SM可容纳的Block 数、每个SM可容纳Warp数、每个SM 可容纳Thread 数都有限制，每个Warp所包含的Thread 数量也是固定的。以Volta 架构的Nvidia Tesla V100为例，其计算能力（Compute Capability）为7.0，对应每个SM 最多可容纳32个Block、64个Warp、2048个Thread，每个Warp 包含的Thread 数量为32。也就意味着，对Tesla V100 而言，Block的大小必须是32的整数倍，且为了使SM 控制的Thread数最大，占用率最高，Block 最小尺寸应大于64（SM可容纳的最大Threads 数/SM 可容纳最大Block 数）。

与此同时，Block的大小又受限于GPU上其他的共享资源，例如：共享内存（Shared Memory），寄存器（Register）。以Nvidia Tesla V100 GPU为 例，GPU上共有65536个大小为32bit的Register，为所有线程共享。若将所有寄存器分配给一个SM，并在一个SM 控制2048个Thread的情况下，则每个Thread中使用的Register 用量最多不超过32。如果Thread 中使用的Register 超过32，CUDA 会强制减少Block 数，从而导致SM 利用率的下降，此时，应尽可能减少Register 使用量，如果Register 用量不能减少，也应适当调整Block的大小，使Block 大小适应SM 可启动的最大线程规模。此外，Shared Memory是Block 内的共享资源，如果对Shared Memory的申请超过最大限额，GPU会从Global Memory 中寻找替代资源，导致核函数执行速度下降，此时应减小Block的大小。

在我们的测试中也发现过大过小的Block 都会影响性能。表2列举了在我们的测试中对6 阶中心差分格式的核函数dx0 设置不同Block 大小时核函数的执行时间，结果发现，对dx0 而言，最合适的Block 大小为32*2*2。不同核函数资源需求量不同，Block的最优尺寸可能也不同，应视情况而定。

表2 线程块大小与函数运算耗时Table2 Thread block size and the time of function operation

3.3 对寄存器、共享内存、常量内存的使用

GPU上的内存层次分为多层。尽可能利用好各种类型的内存资源，如寄存器（Register）、共享内存（Shared Memory）、常量内存（Constant Memory），有利于提高程序性能。

上面已经说到，过多使用寄存器，会导致SM利用率下降，线程并发数量减少，影响程序性能。在我们的程序中，我们令核函数内临时变量尽可能复用，以减少Register的开销，此外也采用将寄存器用量过多的核函数进行拆分的方式减少单个核函数的寄存器用量。

Shared Memory是GPU上可编程缓存，与1级缓存有同样高的访存速度，与Global Memory 相比，延迟低20到30倍，带宽大约高10倍。它可以在核函数外声明，并在核函数内调用，Shared Memory在Block 内是共享的。Nvidia Tesla V100 GPU具有98 304 字节大小的Shared Memory，我们在各个核函数中采用一个名称相同的一维向量作为中间变量，并在Shared Memory 上为其开辟内存。这样可以提高访存速度。在我们的程序中，例如7 阶WENOSYMBO 格式进行数值通量的计算时，先从Global Memory 获取流场数据，加权计算得到通量放在Shared Memory 中再进行最后一步的差分，这样的操作可以使核函数的性能提升20%。

Constant Memory是GPU上一个高速只读内存，将程序始终不变的常量存放于Constant Memeoy 中，也可以提高访问速度，而且能使寄存器用量减少。以7 阶WENO-SYMBO 格式为例，有接近60个常量系数，如果放到寄存器中，势必会导致核函数开销过大进而并发数减少，将这些系数放到Constant Memory 中是保障核函数性能的关键，在我们的测试中，网格量为2563时利用Constant Memory 可以用32*4*4的Block 规模来运行程序，而未使用Constant Memory 时程序最大只能以32*4*2的Block规模运行，并发数和性能都有一倍的差距。

3.4 访存的合并与对齐

GPU在线程操作时以线程束为基本单位，具有一定并发性，而在访存时，GPU也是并发操作的，它利用高访存位宽获取了高的访存带宽。在V100上，访问Global Memroy 时有两种方式：（1）通过1级缓存一次访问128 字节的数据；（2）通过2级缓存一次访问32 字节的数据。GPU默认的访存方式是2级缓存访问。在此情况下，一次访问操作会访问4个双精度数据，为了不浪费访存带宽，最大化提高带宽利用率。在访问时，我们让每一个线程束访问首地址为32 字节（128 字节）整数倍的位置，并获取连续32 字节整数倍的数据。

在我们的程序中，以6 阶中心差分格式核函数dx0为例，为了使访存能够合并，我们在一个kernel中执行两次reinterpret (double 4)，读入8个点的数据，在一个kernel 上进行2个点的差分运算。执行一次reinterpret (double 4)读入的数据长度为32 字节，确保每次获取的都是连续的32 字节数据，此时访存是合并的。在经过这样的优化后，dx0 执行时间从未优化前的349ms 缩减到了147ms，核函数运行速度快了一倍以上。

4 高超声速湍流DNS

钝锥是火箭、导弹等外形的典型头部特征，对钝锥开展DNS 具有重要工程意义。我们通过异构程序使用最多64块GPU对6°攻角，1mm 头半径的小钝头锥开展了DNS，有攻角钝锥边界层流动如图5。

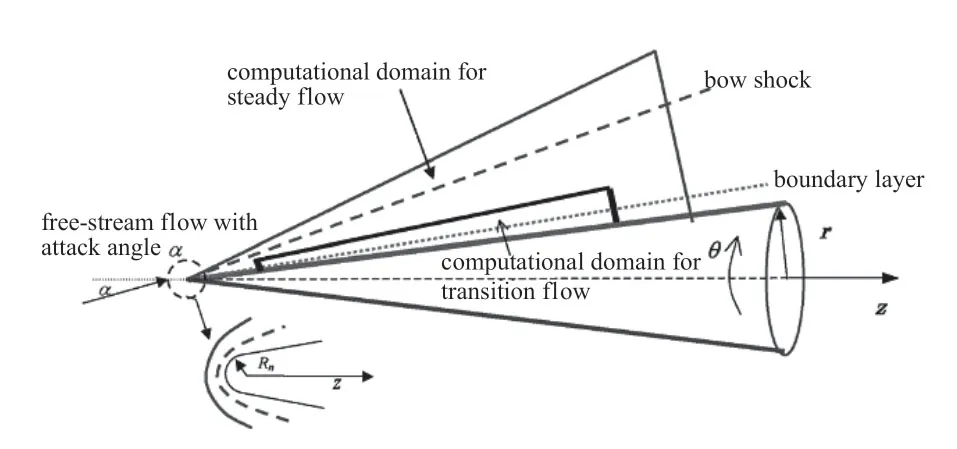
图5 有攻角钝锥边界层流动[21]Fig.5 Schematic of boundary layer flow over a blunt cone with angle of attack[21]

在进行DNS 模拟之前，我们使用粗网格，利用有限体积程序OpenCFD-EC[22]获取定常的层流流场，利用该流场插值出用于DNS的初值与边界条件。

有限体积法的层流计算时，无粘项使用Van Leer分裂与MUSCL 限制器，时间推进采用LU-SGS 方法。

为促进转捩，模拟钝锥表面粗糙单元，在钝锥头部90mm到100mm位置添加吹吸气扰动，扰动幅值为来流速度的千分之一。

4.1 网格与流场设置

参数设置如表3。来流马赫数为6，来流攻角6°，初始壁温为294K，来流温度为79K。钝锥半锥角为7°，头半径为1mm。

表3 流动参数设置Table3 Flow parameter Setting

网格规模为1600*1200*120，其中流线网格数1600，周向网格数1200，法向网格数120，总网格2.3亿，流向网格在头部进行加密，周向采用非均匀网格在迎风面对网格进行加密。壁面第一层网格为0.01mm。流向与周向网格见图6、图7。

图6 钝锥表面流向网格Fig.6 The flow direction's grids of blunt cone

图7 钝锥表面周向网格Fig.7 The circumferential direction's grids of blunt cone

4.2 计算结果

图8为距离头部100 mm、200 mm、300 mm、400mm位置，钝锥表面的热流分布。可以看出钝锥在x=100 mm位置，表面卷起蘑菇状涡，随后在周向表面出现波纹状结构，在x=300 mm位置已经开始转捩，x=400 mm位置流场已经是充分发展的非均匀湍流。

图9是我们绘制的从不同方向观察的钝锥表面摩阻分布。可以看到，由于来流的冲击作用，钝锥下表面迎风面的摩阻明显高于上表面背风面的摩阻。且迎风面摩阻分布较均匀，被风面摩阻分布呈条带状结构。条带状的摩阻结构证明流动已经进入湍流。

图8 钝锥不同位置温度分布Fig.8 Heat flow distribution in different positions of blunt cone

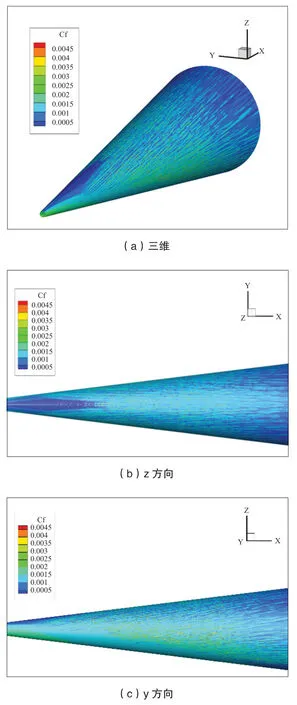
图9 钝锥表面摩阻分布Fig.9 Surface friction distribution of blunt cone

4.3 计算时间

在使用GPU计算之前，我们先使用CPU端的程序OpenCFD-SC 对这一算例计算，使用1024个CPU核心，CPU核心的频率为2.5GHz，系统内存频率为2666MHz，单核峰值性能0.01 TFlops/S。使用此CPU计算每迭代一时间步耗时1.498s（100次迭代取平均）。

而后，我们通过异构程序OpenCFD-SCU 在GPU上对相同算例进行计算，我们使用的GPU频率为1455MHz，显存带宽900GB/S，双精度浮点性能7TFlops/S。我们分别使用16、32、48、64块GPU卡对其进行计算，表4列出了在这4种规模下，计算每迭代一时间步所耗时间（100次迭代取平均）。

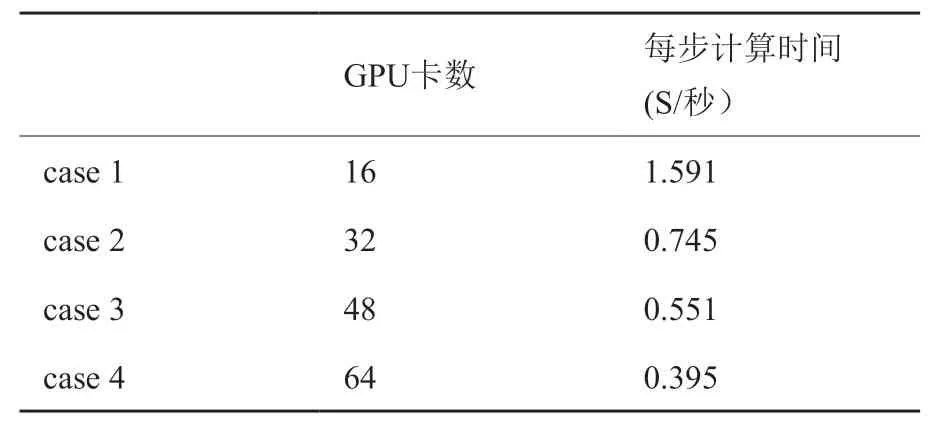
表4 不同GPU数量，每步迭代耗时Table4 Wall time per iteration using different numbers of GPU

可以看出，在使用16块GPU卡对钝锥算例进行计算时，每步迭代时间已经接近使用1024个CPU核心进行计算的时间。程序在单块GPU上取得了比单个CPU核心快60倍的加速效果。使用更多GPU卡，单GPU比单CPU加速效果甚至更明显。图10、图11中展示了在GPU上程序的加速比与并行效率，可以看出有超线性的情况，这可能是此算例对16个GPU而言负载过大，但也可以看出，OpenCFD-SCU程序整体扩展性很好，在最大64块GPU卡上，并行效率基本没有变化。

在整个算例的计算中，我们迭代了10万步，使用64块GPU只用11个小时左右就得出了结果，而以往对相同类型算例的计算，使用200 余个主频2.5GHz的CPU核心，往往需要花费一周时间。如果是对更大规模的算例，可能需要数月时间，利用GPU能将耗时缩短一个数量级。

图10 GPU程序加速比Fig.10 GPUprogram speedup

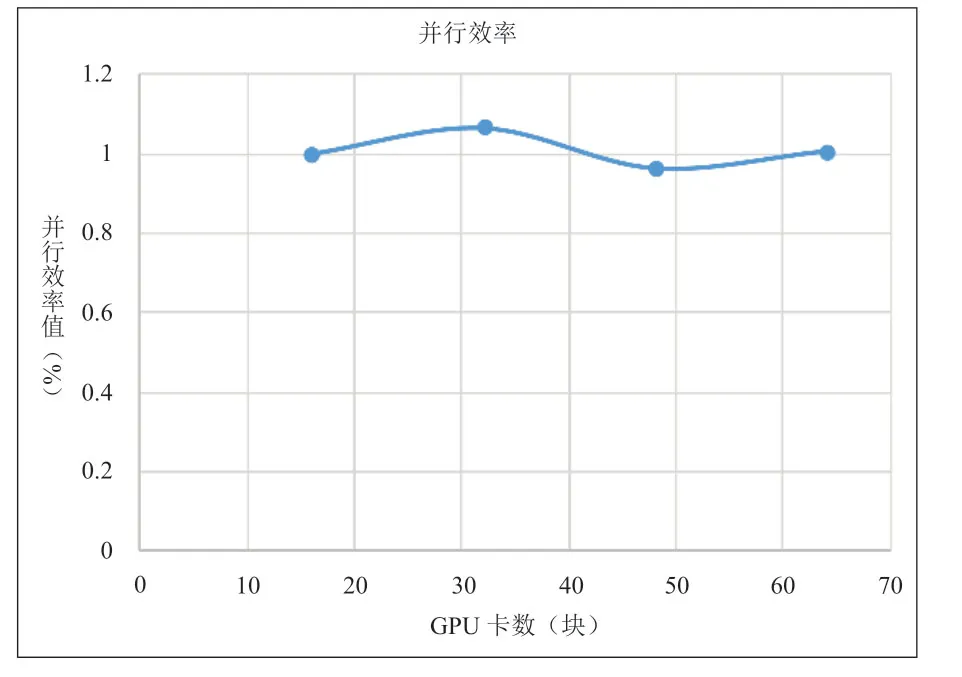
图11 GPU程序并行效率Fig.11 Program parallel efficiency

5 小结

本文介绍了GPU在高超声速湍流计算上的应用。描述了GPU程序优化相关技术，并使用CPU/GPU异构程序对来流马赫数为6的6°攻角小钝头锥开展了DNS。

结果表明，GPU可以胜任高超声速湍流直接数值模拟，并能取得了较好的加速效果，程序在单GPU上比单CPU核加速了60倍，大大缩短了模拟时间。可以想象，在未来会有更多高超声速湍流模拟问题在GPU上开展。

目前，OpenCFD-SCU的功能模块尚不够丰富，核函数还有优化空间，未来将继续添加功能以适应更多不同的算例，还将对核函数进行深度优化，以提升程序性能。此外，在程序结构上，目前仍采用单线程阻塞式MPI 通讯，为加速整体性能，未来将对程序结构做调整，完成CPU上计算与MPI 通讯重叠，在GPU方面，也将使用更多流（Stream）操作来提升GPU并发性，并使GPU上的计算与主机、设备间内存拷贝进行重叠，进而提升整体性能。

利益冲突声明

所有作者声明不存在利益冲突关系。